How to Solve LPP with Simplex Method?

Mathematics Satyam January 28, 2024 Linear Programming No Comments

Contents hide

1 1.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method):

1.1 2.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें पर आधारित उदाहरण (Examples Based on How to Solve LPP with Simplex Method?):

1.2 3.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें पर आधारित सवाल (Questions Based on How to Solve LPP with Simplex Method?):

1.2.1 4.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (Frequently Asked Questions Related to How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.सिम्पलेक्स विधि की अभिकलनी प्रक्रिया क्या है? (What is Computational Procedure of Simplex Method?):

1.2.3 प्रश्न:2.समस्या को अधिकतमीकरण की समस्या में कैसे बदलते हैं? (How Do You Convert Problem into that of Maximization?):

1.2.4 प्रश्न:3.b के सभी घटकों को धनात्मक कैसे बनाते हैं? (How to Make all the b’s Positive?):

1.2.4.1 How to Solve LPP with Simplex Method?

2 एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?)

2.1 How to Solve LPP with Simplex Method?

1.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method):

How to Solve LPP with Simplex Method?

एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?) के इस आर्टिकल में कुछ सवालों को सिम्पलेक्स विधि द्वारा हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:- Median and Simple Arithmetic Mean

2.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें पर आधारित उदाहरण (Examples Based on How to Solve LPP with Simplex Method?):

निम्न रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल कीजिए:
(Solve the following L.P.P. by simplex method):
Example:10.निम्नतम (min.) $Z=x_1+x_2+3 x_3$
प्रतिबन्ध (s.t.) $3 x_1+2 x_2+x_3 \leq 3 \\ 2 x_1+x_2+2 x_3 \leq 2$
तथा (and) $x_1, x_2, x_3 \geq 0$
Solution:सर्वप्रथम उद्देश्य फलन को अधिकतमीकरण की समस्या में बदलते हैं चूँकि यह निम्नतमीकरण की समस्या है।तत्पश्चात प्रतिबन्ध असमिकाओं को न्यूनतापरक चर $x_4$ तथा $x_5$ की सहायता से समीकरणों में बदलते हैं।
अतः समस्या का मानक रूप होगा:
अधिकतम (max.) $Z'=-x_1-x_2-3 x_3+0 x_4+0 x_5$
प्रतिबन्ध (s.t.) $3 x_1+2 x_2+x_3+x_4+0 x_5=3 \\ 2 x_1+x_2+2 x_3+0 x_4+x_5=2$
तथा (and) $x_1, x_2, x_3, x_4, x_5 \geq 0$
मानलो प्रतिबन्ध निकाय में गुणांक मैट्रिक्स A है तब

$A=\left[\begin{array}{lllll} 3 & 2 & 1 & 1 & 0 \\ 2 & 1 & 2 & 0 & 1 \end{array}\right]=\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5\right) \\ \left(\alpha_4, \alpha_5\right)=I_2$ अतः प्रारम्भिक आधार $B=\left(\alpha_4 \alpha_5\right)$ तथा प्रारम्भिक सिम्पलेक्स सारणी निम्न प्रकार होगी:
प्रथम सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|ccccc|} \hline & & & C_{i} \rightarrow & -1 & -1 & -3 & 0 & 0 \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 \\ \hline 0 & \alpha_4 & x_4 & 3 & 3 & 2 & 1 & 1 & 0 \\ \hline 0 & \alpha_5 & x_5 & 2 & 2 & 1 & 2 & 0 & 1 \\ \hline & & & Z_{j}-C_{j} & 1 & 1 & 3 & 0 & 0 \\ \hline & & & & & & \uparrow & \downarrow & \end{array}$
उपर्युक्त सारणी में $Z_{j}-C_{j}$ के सभी मान $\geq$ है,अतः इसका आधारी हल इष्टतम होगा जो निम्न प्रकार है:

$x_1=0, x_2=0, x_3=0, x_4=3, x_5=2$
अतः दी गई रैखिक प्रोग्रामन समस्या का इष्टतम हल है:

$x_1=0, x_2=0, x_3=0$
तथा अधिकतम $(Z')=-x_1-x_2-3 x_3+0 x_1+0 x_4+0 x_5 \\ =-0-0-3(0)+0(2)+0(3) \\ =0$
अतः निम्नतम (Z)=0 [Max. Z’=0]
Example:11.अधिकतम (max.) $Z=4 x_1+x_2+3 x_3+5 x_4$
प्रतिबन्ध (s.t.) $4 x_1-6 x_2-5 x_3+4 x_4 \geq -20 \\ 3 x_1-2 x_2+4 x_3+x_4 \leq 10 \\ 8 x_1-3 x_2+3 x_3+2 x_4 \leq 20$
तथा (and) $x_1, x_2, x_3, x_4 \geq 0$
Solution:b के सभी घटकों को धनात्मक बनाने परः

अधिकतम (max.) $Z=4 x_1+x_2+3 x_3+5 x_4$
प्रतिबन्ध (s.t.) $-4 x_1+6 x_2+5 x_3-4 x_4 \leq -20 \\ 3 x_1-2 x_2+4 x_3+x_4 \leq 10 \\ 8 x_1-3 x_2+3 x_3+2 x_4 \leq 20$
प्रतिबन्ध असमिकाओं में न्यूनतापूरक चरों $x_5, x_6$ तथा $x_7$ को सम्मिलित करने से समस्या का मानक रूप होगा।

Max. $Z=4 x_1+x_2+3 x_3+5 x_4+0 x_5+0 x_6+0 x_7$
s.t. $-4 x_1+6 x_2+5 x_3-4 x_4+x_5+0 x_6+0 x_4=20 \\ 3 x_1-2 x_2+4 x_3+x_4+0 x_5+x_6+0 x_7=10 \\ 8 x_1-3 x_2+3 x_3+2 x_4+0 x_5+0 x_6+x_7=20$
तथा $x_1, x_2, x_3, x_4, x_5, x_6, x_7 \geq 0$
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
$A=\left[\begin{array}{ccccccc} -4 & 6 & 5 & -4 & 1 & 0 & 0 \\ 3 & -2 & 4 & 1 & 0 & 1 & 0 \\ 8 & -3 & 3 & 2 & 0 & 0 & 1\end{array}\right]=\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6\right)$ (मानलो)
$\therefore \left(\alpha_5 \alpha_5 \alpha_7\right)=I_3$ , अतः प्रारम्भिक आधार $B=\left(\alpha_5 \alpha_6 \alpha_7\right)$ एवं प्रारम्भिक सारणी निम्न प्रकार होगी:
प्रथम सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|ccccccc|} \hline & & & C_{i} \rightarrow & 4 & 1 & 3 & 5 & 0 & 0 & 0 \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 & y_7 \\ \hline 0 & \alpha_5 & x_5 & 20 & -4 & 6 & 5 & -4 & 1 & 0 & 0 \\ \hline 0 & \alpha_6 & x_6 & 10 & 3 & -2 & 4 & 1 & 0 & 1 & 0\\ \hline 0 & \alpha_7 & x_7 & 20 & 8 & -3 & 3 & \fbox{2} & 0 & 0 & 1 \\ \hline & & & Z_{j}-C_{j} & -4 & -1 & -3 & -5 & 0 & 0 & 0 \\ \hline & & & & & & & \uparrow & & &\downarrow \end{array}$
$Z_{j}-C_{j}$ के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है।चूँकि $Z_{4}-C_{4}=-5$ निम्नतम है,अतः नवीन आधारी हल हेतु $\alpha_4$ प्रवेशी सदिश होगा एवं
$\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 4}}, y_{i 4}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{10}{1}, \frac{20}{2}\right\} \\ =(1,1)$
चूँकि निम्नतम 1 है,अतः $\alpha_6$ तथा $\alpha_7$ दोनों अपगामी सदिश होंगे।माना $\alpha_7$ को ही अपगामी सदिश लेते हैं।सामान्य रूपान्तरणों द्वारा नवीन सारणी निम्न प्रकार होगी:
मुख्य अवयव वाली पंक्ति (Working rule):
मुख्य अवयव है 2 है अतः तृतीय पंक्ति के सभी अवयवों को 2 से विभाजित करने पर मुख्य अवयव वाली पंक्ति तैयार होगी:

$\frac{20}{2}=10, \frac{8}{2}=4,-\frac{3}{2}, \frac{3}{2}, \frac{2}{2}=1, \frac{0}{2}=0, \frac{0}{2}=0, \frac{1}{2}$
प्रथम पंक्ति:प्रथम सिम्पलेक्स सारणी के मुख्य अवयव $y_{34}=2$ के संगत प्रथम पंक्ति का अवयव -4 है।अतः प्रथम पंक्ति के अवयवों में से मुख्य अवयव (द्वितीय सिम्पलेक्स सारणी के लिए प्रयुक्त) वाली पंक्ति के अवयवों अर्थात् उपर्युक्त अवयवों को -4 से गुणा करके घटा देते हैं:
$20-10 \times-4=60,-4-2 \times-4=12,6-\left(-\frac{3}{2}\right) \times-4 =0,5-\frac{3}{2} \times-4=11, \\-4-1 \times-4=0,1-0 \times-4=1 ,0-0 \times-4=0,0-\frac{1}{2} \times-4=2$
द्वितीय पंक्ति:प्रथम सिम्पलेक्स सारणी की द्वितीय पंक्ति के अवयवों में से मुख्य अवयव के संगत अवयव 1 को मुख्य अवयव वाली पंक्ति के अवयवों से गुणा करके घटा देने पर द्वितीय सिम्पलेक्स सारणी की द्वितीय पंक्ति तैयार होगी:
$10-10 \times 1=0,3-4 \times 1=-1,-2-\left(-\frac{3}{2}\right) \times 1 =-\frac{1}{2}, 4-\frac{3}{2} \times 1=\frac{5}{2} \\ 1-1 \times 1=0,0-0 \times 1=0,1-0 \times 1=1,0-\frac{1}{2} \times 1=-\frac{1}{2}$
द्वितीय सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|ccccccc|} \hline & & & C_{i} \rightarrow & 4 & 1 & 3 & 5 & 0 & 0 & 0 \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 & y_7 \\ \hline 0 & \alpha_5 & x_5 & 60 & 12 & 0 & 11 & 0 & 1 & 0 & 2 \\ \hline 0 & \alpha_6 & x_6 & 0 & -1 & -\frac{1}{2} & \frac{5}{2} & 0 & 0 & 1 & -\frac{1}{2}\\ \hline 0 & \alpha_4 & x_4 & 10 & 4 & -\frac{3}{2} & \frac{3}{2} & 1 & 0 & 0 & \frac{1}{2} \\ \hline & & & Z_{j}-C_{j} & 16 & -\frac{17}{2} & \frac{9}{2} & 0 & 0 & 0 & \frac{5}{2} \\ \hline \end{array}$
$Z_2-C_2=-\frac{17}{2}$ का मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है।परन्तु के सभी मान ऋणात्मक और 0 से बड़ा नहीं होने के कारण समस्या का हल अपरिबद्ध (unbounded) है।

How to Solve LPP with Simplex Method?

Example:12.अधिकतम (Max.) $Z=107 x_1+x_2+x_3$
प्रतिबन्ध (s.t.) $\frac{14}{3} x_1+\frac{1}{3} x_2-2 x_3+x_4=\frac{7}{3} \\ 16 x_1+\frac{1}{2} x_2-6 x_3 \leq 0 \\ 3 x_1-x_2-x_3 \leq 0$
तथा (and) $x_1, x_2, x_3, x_4 \geq 0$
Solution:प्रतिबन्ध असमिकाओं में न्यूनतापूरक चर $x_5$ व $x_6$ की सहायता से समीकरणों में बदलते हैं।अतः परिवर्तित समस्या होगी:

Max. $Z=107 x_1+x_2+x_3+0 x_4+0 x_5+0 x_6$
s.t. $\frac{14}{3} x_1+\frac{1}{3} x_2-2 x_3+x_4+0 x_5+0 x_6=\frac{7}{3} \\ 16 x_1+\frac{1}{2} x_2-6 x_3+0 x_4+x_5+0 x_6=0 \\ 3 x_1-x_2-x_3+0 x_4+0 x_5+x_6=0$
and $x_1, x_2, x_3, x_4 , x_5 , x_6 \geq 0$
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
$A=\left[\begin{array}{cccccc} \frac{14}{3} & \frac{1}{3} & -2 & 1 & 0 & 0 \\ 16 & \frac{1}{2} & -6 & 0 & 1 & 0 \\ 3 & -1 & -1 & 0 & 0 & 1 \end{array}\right]=\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6\right)$ (मानलो)
अतः प्रारम्भिक आधार $B=\left( \alpha_4 \alpha_5 \alpha_6\right)$ एवं प्रारम्भिक सारणी निम्न प्रकार होगी:
प्रथम सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|cccccc|} \hline & & & C_{i} \rightarrow & 107 & 1 & 1 & 0 & 0 & 0 \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 \\ \hline 0 & \alpha_4 & x_4 & \frac{7}{3} & \frac{14}{3} & \frac{1}{3} & -2 & 1 & 0 & 0 \\ \hline 0 & \alpha_5 & x_5 & 0 & \fbox{16} & \frac{1}{2} & -6 & 0 & 1 & 0 \\ \hline 0 & \alpha_6 & x_6 & 0 & 3 & -1 & -1 & 0 & 0 & 1 \\ \hline & & & Z_{j}-C_{j} & -107 & -1 & -1 & 0 & 0 & 0 \\ \hline \end{array}$
$Z_{j}-C_{j}$ के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम नहीं है।चूँकि $Z_{j}-C_{j}=-107$ निम्नतम है,अतः नवीन आधारी हल हेतु प्रवेशी सदिश होगा एवं
$\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 1}}, y_{i 1}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{\frac{7}{3}}{\frac{14}{3}},\frac{0}{16},\frac{0}{13} \right\} \\ =(0,0)$
चूँकि निम्नतम मान 0 है,अतः $\alpha_5$ तथा $\alpha_6$ दोनों ही अपगामी सदिश होंगे।माना $\alpha_5$ को ही अपगामी सदिश लेते हैं।अतः $y_{21}$ अर्थात् 16 मुख्य अवयव (key element) है।सामान्य रूपान्तरणों द्वारा नवीन सारणी निम्न प्रकार होगी:
द्वितीय सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|cccccc|} \hline & & & C_{i} \rightarrow & 107 & 1 & 1 & 0 & 0 & 0 \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 \\ \hline 0 & \alpha_4 & x_4 & \frac{7}{3} & 0 & -\frac{17}{16} & 0 & 1 & -\frac{85}{168} & \frac{8}{7} \\ \hline 107 & \alpha_1 & x_1 & 0 & 1 & -\frac{13}{4} & 0 & 0 & -\frac{1}{2} & 3 \\ \hline 0 & \alpha_3 & x_3 & 0 & 0 & -\frac{35}{4} & 1 & 0 & -\frac{3}{2} & 8 \\ \hline & & & Z_{j}-C_{j} & 0 & -\frac{1395}{4} & 0 & 0 & -\frac{107}{2} & 329 \\ \hline & & & & & \uparrow & & \downarrow & & \end{array}$
$Z_{j}-C_{j}$ के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम नहीं है।परन्तु के सभी मान ऋणात्मक होने के कारण समस्या का हल अपरिबद्ध (unbounded) है।
Example:13.अधिकतम (Max.) $Z=2 x_1-x_2+x_3$
प्रतिबन्ध (s.t.) $x_1+x_2-3 x_3 \leq 8 \\ 4 x_1-x_2+x_3 \geq 2 \\ 2 x_1+3 x_2+x_3 \geq 4$
तथा (and) $x_1, x_2, x_3 \geq 0$
Solution:प्रतिबन्ध असमिकाओं के क्रमशः न्यूनतापूरक चर $x_4$ तथा आधिक्यपूरक चर $x_5, x_6$ द्वारा समीकरण में बदलते हैं।अतः परिवर्तित समस्या होगी:
Max $Z=2 x_1-x_2+x_3+0 x_4+0 x_5+0 x_6$
s.t. $x_1+x_2-3 x_3+x_4+0 x_5+0 x_6=8 \\ 4 x_1-x_2+x_3+0 x_4-x_5+0 x_6=2 \\ 2 x_1+3 x_2+x_3+0 x_4+a x_5-x_6=4$
तथा $x_1, x_2, x_3, x_4, x_5, x_6 \geq 0$
परन्तु गुणांक मैट्रिक्स में एकक उपमैट्रिक्स विद्यमान नहीं है,अतः असमिकाओं में कृत्रिम चर $x_7$ तथा $x_8$ सम्मिलित करेंगे तथा उद्देश्य फलन में इनके मूल्य -M रखेंगे जहाँ M एक बहुत बड़ी संख्या है।
अतः समस्या का मानक रूप होगा:
Max. $Z=2 x_1 -x_2+x_3+0 x_4+0 x_5+0 x_6-M x_7-M x_8=0$
s.t. $x_1+x_2-3 x_3+x_4+0 x_5+0 x_6+0 x_7+0 x_8=8 \\ -4 x_1-x_2+x_3+0 x_4-x_5+0 x_6+x_7+0 x_8=2 \\ 2 x_1+3 x_2+x_3+0 x_4+0 x_5-x_6+0 x_7+x_8=4$
तथा $x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8 \geq 0$
प्रतिबन्ध निकाय में गुणांक मैट्रिक्स
$A=\left[\begin{array}{cccccccc}1 & 1 & -3 & 1 & 0 & 0 & 0 & 0 \\ -4 & -1 & 1 & 0 & -1 & 0 & 1 & 0 \\2 & 3 & 1 & 0 & 0 & -1 & 0 & 1\end{array}\right]=\left(\alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6 \alpha_7 \alpha_8\right)$ (मानलो)
$\therefore \left(\alpha_4 \alpha_7 \alpha_8\right)=I_3$ , अतः प्रारम्भिक आधार $B=\left(\alpha_4 \alpha_7 \alpha_8\right)$ तथा प्रारम्भिक सारणी निम्न होगी:
प्रथम सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|cccccccc|} \hline & & & C_{i} \rightarrow & 2 & -1 & 1 & 0 & 0 & 0 & -M & -M \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 & y_7 & y_8 \\ \hline 0 & \alpha_4 & x_4 & 8 & 1 & 1 & -3 & 1 & 0 & 0 & 0 & 0 \\ \hline -M & \alpha_7 & x_7 & 2 & -4 & -1 & \fbox{1} & 0 & -1 & 0 & 1 & 0 \\ \hline -M & \alpha_8 & x_8 & 4 & 2 & 3 & 1 & 0 & 0 & -1 & 0 & 1 \\ \hline & & & Z_{j}-C_{j} & 2M-2 & -2M+1 & -2M-1 & 0 & M & M & 0 & 0 \\ \hline & & & & & & \uparrow & & & & \downarrow & \end{array}$
उपर्युक्त आधारी हल इष्टतम हल नहीं है चूँकि $Z_j-C_j$ के कुछ मान ऋणात्मक हैं, जिसमें निम्नतम $Z_3-C_3=-2M-1$ है,अतः प्रवेशी सदिश होगा $\alpha_3$ एवं
अर्थात् 1 मुख्य अवयव (key element) तथा अपगामी सदिश होगा,जिसे कृत्रिम चर होने के कारण नई सारणी में सम्मिलित नहीं करेंगे।अतः सामान्य रूपान्तरणों द्वारा नवीन सारणी इस प्रकार होगी:
द्वितीय सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|ccccccc|} \hline & & & C_{i} \rightarrow & 2 & -1 & 1 & 0 & 0 & 0 & -M \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 & y_8 \\ \hline 0 & \alpha_4 & x_4 & 14 & -11 & -2 & 0 & 1 & -3 & 0 & 0 \\ \hline 1 & \alpha_3 & x_3 & 2 & -4 & -1 & 1 & 0 & -1 & 0 & 0 \\ \hline -M & \alpha_8 & x_8 & 2 & \fbox{6} & 4 & 0 & 0 & 1 & -1 & 1 \\ \hline & & & Z_{j}-C_{j} & -6M-6 & -4M & 0 & 0 & -M-1 & M & 0 \\ \hline & & & & \uparrow & & & & & & \downarrow & \end{array}$
उपर्युक्त आधारी हल इष्टतम हल नहीं है चूँकि $Z_j-C_j$ के कुछ मान ऋणात्मक है,जिसमें $Z_1-C_1=-6M-6$ निम्नतम है,अतः $\alpha_1$ प्रवेशी सदिश होगा एवं
$\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 3}}, y_{i 3}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{2}{1},\frac{4}{1} \right\} =\frac{2}{1}=\frac{x_{B2}}{y_{23}} \\ \therefore y_{23}$
अर्थात् 6 मुख्य अवयव (key element) तथा अपगामी सदिश होगा,जिसे कृत्रिम चर होने के कारण नई सारणी में सम्मिलित नहीं करेंगे।अतः सामान्य रूपान्तरणों द्वारा नवीन सारणी इस प्रकार होगी:
तृतीय सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|cccccc|} \hline & & & C_{i} \rightarrow & 2 & -1 & 1 & 0 & 0 & 0 \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 \\ \hline 0 & \alpha_4 & x_4 & \frac{53}{3} & 0 & \frac{16}{3} & 0 & 1 & -\frac{7}{6} & -\frac{11}{6} \\ \hline 1 & \alpha_3 & x_3 & \frac{10}{3} & 0 & \frac{5}{3} & 1 & 0 & -\frac{1}{3} & -\frac{2}{3} \\ \hline 2 & \alpha_1 & x_1 & \frac{1}{3} & 1 & \frac{2}{3} & 0 & 0 & \frac{1}{6} & -\frac{1}{6} \\ \hline & & & Z_{j}-C_{j} & 0 & 4 & 0 & 0 & 0 & -1 \\ \hline \end{array}$
$Z_6-C_6$ ऋणात्मक होने के कारण आधारी हल इष्टतम नहीं है।परन्तु $y_6$ के सभी मान ऋणात्मक होने के कारण समस्या का हल अपरिबद्ध (unbounded) है।
Example:14.अधिकतम (Max.) $Z=4 x_1+3 x_2$
प्रतिबन्ध (s.t.) $x_1+x_2 \leq 50 \\ x_1+2 x_2 \geq 80 \\ 3 x_1+2 x_2 \geq 140$
तथा (and) $x_1, x_2>0$
Solution:समस्या के प्रतिबन्ध निकाय में न्यूनतापूरक चर $x_3$ तथा आधिक्यपूरक चर $x_4, x_5$ तथा उनके संगत उद्देश्य फलन में शून्य मूल्य सहित $x_3, x_4$ व $x_5$ को सम्मिलित करने पर समस्या का परिवर्तित रूप निम्न प्रकार होगा:
Max. $Z=4 x_1+3 x_2+0 x_3+0 x_4+0 x_5$
s.t. $x_1+x_2+x_3+0 x_4+0 x_5=30 \\ x_1+2 x_2+0 x_3-x_4+0 x_5=80 \\ 3 x_1+2 x_2+0 x_3+0 x_4-x_5=140$
तथा $x_1, x_2, x_3, x_4, x_5 \geq 0$
परन्तु गुणांक मैट्रिक्स में एकक उपमैट्रिक्स विद्यमान नहीं है अतः समस्या के प्रतिबन्ध समीकरणों में कृत्रिम चरों $x_6$ तथा $x_7$ एवं उनके संगत उद्देश्य फलन में -M रखने पर, जहाँ M एक बहुत बड़ी धनात्मक संख्या है।समस्या का मानक रूप होगा:
Max. $Z=4 x_1+3 x_2+0 x_3+0 x_4+0 x_5-M z_6-M x_6$
s.t. $x_1+x_2+x_3+0 x_4+0 x_5+0 x_6+0 x_7=50 \\ x_1+2 x_2+0 x_3-x_4+0 x_5+x_6+0 x_7=80 \\ 3 x_1+2 x_2+0 x_3+0 x_4-x_5+0 x_6+x_7=140$
तथा $x_1, x_2, x_3, x_4, x_5, x_6, x_7 \geq_0$
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
$A=\left[\begin{array}{ccccccc}1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 2 & 0 & -1 & 0 & 1 & 0 \\ 3 & 2 & 0 & 0 & -1 & 0 & 1\end{array}\right]=\left( \alpha_1 \alpha_2 \alpha_3 \alpha_4 \alpha_5 \alpha_6 \alpha_7\right)$ (मानलो)
$\therefore \left(\alpha_3 \alpha_6 \alpha_7\right)=I_3$ ; अतः प्रारम्भिक आधार एवं $B=\left(\alpha_3 \alpha_6 \alpha_7\right)$ प्रारम्भिक सारणी निम्न प्रकार होगी:
प्रथम सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|ccccccc|} \hline & & & C_{i} \rightarrow & 4 & 3 & 0 & 0 & 0 & -M & -M \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 & y_7 \\ \hline 0 & \alpha_3 & x_3 & 50 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline -M & \alpha_6 & x_6 & 80 & 1 & 2 & 0 & -1 & 0 & 1 & 0 \\ \hline -M & \alpha_7 & x_7 & 140 & \fbox{3} & 2 & 0 & 0 & -1 & 0 & 1 \\ \hline & & & Z_{j}-C_{j} & -4M-4 & -4M-3 & 0 & M & M & 0 & 0 \\ \hline & & & & \uparrow & & & & & &\downarrow \end{array}$
उपर्युक्त आधारी हल इष्टतम हल नहीं है चूँकि $Z_j-C_j$ के कुछ मान ऋणात्मक हैं,जिनमें $Z_1-C_1=-4M-4$ निम्नतम है,अतः $\alpha_1$ प्रवेशी सदिश होगा एवं
$\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 1}}, y_{i 1}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{50}{1},\frac{80}{1},\frac{140}{3} \right\} =\frac{140}{3}=\frac{x_{B3}}{y_{31}} \\ \therefore y_{31}$ अर्थात् 3 मुख्य अवयव (key element) तथा $\alpha_7$ अपगामी सदिश होगा जिसे कृत्रिम चर होने के कारण नई सारणी में सम्मिलित नहीं करेंगे।अतः सामान्य रूपान्तरणों द्वारा नवीन सारणी इस प्रकार होगीः
मुख्य अवयव वाली पंक्ति (working rule):
मूख्य अवयव वाली तीसरी पंक्ति है अतः इसके प्रत्येक अवयव में मुख्य अवयव 3 का भाग देने पर द्वितीय सिम्पलेक्स सारणी हेतु तृतीय पंक्ति तैयार होगी।

$\frac{140}{3}, \frac{3}{3}=1, \frac{2}{3}, \frac{0}{3}=0, \frac{0}{3}=0,-\frac{1}{3}, \frac{0}{3}=0$
प्रथम पंक्ति:प्रथम सिम्पलेक्स सारणी की प्रथम पंक्ति के अवयवों में मुख्य अवयव वाली पंक्ति के अवयवों अर्थात उपर्युक्त अवयवों को मुख्य अवयव के संगत प्रथम पंक्ति के अवयव 1 से गुणा करके घटा देंगे:
$\frac{140}{3} \times 1=\frac{10}{3}, 1-1 \times 1=0,1-\frac{2}{3} \times 1=\frac{1}{3}, \\ 1-0 \times 1=1,0-0 \times 1=0,0-(-\frac{1}{3}) \times 1=\frac{1}{3} , 0-0 \times 1=0$
द्वितीय पंक्ति:प्रथम सिम्पलेक्स सारणी की द्वितीय पंक्ति के अवयवों में मुख्य अवयव वाली पंक्ति के अवयवों जो द्वितीय सारणी की तृतीय पंक्ति के लिए तैयार किए गए हैं,को मुख्य अवयव के संगत द्वितीय पंक्ति के अवयव 1 से गुणा करके घटा देंगे:
$80-\frac{140}{3} \times 1=\frac{100}{3}, 1-1 \times 1=0,2-\frac{2}{3} \times 1=\frac{4}{3}, \\ 0-0 \times 1=0,-1-0 \times 1=-1,0-\left( -\frac{1}{3} \right) \times 1=\frac{1}{3},1-0 \times 1=1$
द्वितीय सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|cccccc|} \hline & & & C_{i} \rightarrow & 4 & 3 & 0 & 0 & 0 & -M \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 \\ \hline 0 & \alpha_3 & x_3 & \frac{10}{3} & 0 & \frac{\fbox{1}}{\fbox{3}} & 1 & 0 & \frac{1}{3} & 0 \\ \hline -M & \alpha_6 & x_6 & \frac{100}{3} & 0 & \frac{4}{3} & 0 & -1 & \frac{1}{3} & 1 \\ \hline 4 & \alpha_1 & x_1 & \frac{140}{3} & 1 & \frac{2}{3} & 0 & 0 & -\frac{1}{3} & 0 \\ \hline & & & Z_{j}-C_{j} & 0 & -\frac{4M}{3}-\frac{1}{3} & 0 & M & -\frac{M}{3}-\frac{4}{3} & 0 \\ \hline & & & & & \uparrow & \downarrow & & & \end{array}$
उपर्युक्त आधारी हल इष्टतम हल नहीं है चूँकि $Z_j-C_j$ के कुछ मान ऋणात्मक हैं,जिसमें $Z_2-C_2=-\frac{4 M}{3}-\frac{1}{3}$ निम्नतम है,अतः $\alpha_2$ प्रवेशी सदिश होगा एवं
$\underset{i}{\text{निम्नतम}}\left\{\frac{x_{B i}}{y_{i 2}}, y_{i 2}>0\right\}=\underset{i}{\text{निम्नतम}}\left\{\frac{\frac{10}{3}}{\frac{1}{3}},\frac{\frac{100}{3}}{\frac{4}{3}},\frac{\frac{140}{3}}{\frac{2}{3}} \right\} =\frac{\frac{10}{3}}{\frac{1}{3}}=\frac{x_{B1}}{y_{12}} \\ \therefore y_{12}$ अर्थात् $\frac{1}{3}$ मुख्य अवयव (key element) तथा $\alpha_3$ अपगामी सदिश होगा।अतः सामान्य रूपान्तरणों द्वारा नवीन सारणी निम्न प्रकार होगी:
मुख्य अवयव वाली पंक्ति (working rule):
मुख्य अवयव वाली प्रथम पंक्ति में मुख्य अवयव $\frac{1}{3}$ का भाग देने पर तृतीय सारणी की प्रथम पंक्ति तैयार होगी:

$\frac{\frac{10}{3}}{\frac{1}{3}}=10, \frac{0}{\frac{1}{3}}=0, \frac{\frac{1}{3}}{\frac{1}{3}}=1, \frac{1}{\frac{1}{3}}=3, \frac{0}{\frac{1}{3}}=0 ,\frac{\frac{1}{3}}{\frac{1}{3}}=1, \frac{0}{\frac{1}{3}}=0$
द्वितीय पंक्ति:द्वितीय सिम्पलेक्स सारणी की द्वितीय पंक्ति के अवयवों में से मुख्य अवयव वाली पंक्ति के अवयवों अर्थात् उपर्युक्त अवयवों को मुख्य अवयव के संगत द्वितीय पंक्ति के अवयव $\frac{4}{3}$ से गुणा करके घटा देंगे:

$\frac{100}{3}-10 \times \frac{4}{3}=20,0-0 \times \frac{4}{3}=0, \frac{4}{3}-1 \times \frac{4}{3}=0 \\ 0-3 \times \frac{4}{3}=-4,-1-0 \times \frac{4}{3}=-1, \frac{1}{3}-1 \times \frac{4}{3}=-1 , 1-0 \times \frac{4}{3}=1$
तृतीय पंक्ति:द्वितीय सिम्पलेक्स सारणी की तृतीय पंक्ति के अवयवों में से मुख्य अवयव वाली पंक्ति के अवयवों को मुख्य अवयव के संगत तृतीय पंक्ति के अवयव $\frac{2}{3}$ से गुणा करके घटा देंगे:

$\frac{140}{3}-10 \times \frac{2}{3}=40,1-0 \times \frac{2}{3}=1, \frac{2}{3}-1 \times \frac{2}{3}=0, \\ 0-3 \times \frac{2}{3}=-2,0-0 \times \frac{2}{3}=0,-\frac{1}{3}-1 \times \frac{2}{3}=-1 , 0-0 \times \frac{2}{3}=0$
तृतीय सिम्पलेक्स सारणी

$\begin{array}{|ccc|c|cccccc|} \hline & & & C_{i} \rightarrow & 4 & 3 & 0 & 0 & 0 & -M \\ \hline C_{B} & B & X_B & b & y_1 & y_2 & y_3 & y_4 & y_5 & y_6 \\ \hline 3 & \alpha_2 & x_2 & 10 & 0 & 1 & 3 & 0 & 1 & 0 \\ \hline -M & \alpha_6 & x_6 & 20 & 0 & 0 & -4 & -1 & -1 & 1 \\ \hline 4 & \alpha_1 & x_1 & 40 & 1 & 0 & -2 & 0 & -1 & 0 \\ \hline & & & Z_{j}-C_{j} & 0 & 0 & 4M+1 & M & M-1 & 0 \\ \hline \end{array}$
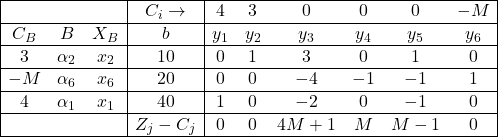
उपर्युक्त सारणी $Z_j-C_j$ के सभी मान धनात्मक $\left( \geq \right)$ हैं परन्तु आधार में कृत्रिम चर $\alpha_6$ के संगत चर अशून्य है,अतः समस्या का कोई सुसंगत हल विद्यमान नहीं है।
उपर्युक्त उदाहरणों के द्वारा एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method) को समझ सकते हैं।

3.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें पर आधारित सवाल (Questions Based on How to Solve LPP with Simplex Method?):

How to Solve LPP with Simplex Method?

निम्न रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल कीजिए:
(Solve the following L.P.P. by simplex method):

(1.) Maximize $Z=10 x_1+x_2+2 x_3$
subject to: $x_1+x_2-2 x_3 \leq 10 \\ 4 x_1+x_2+x_3 \leq 20$
and $x_1, x_2, x_3 \geq 0$
(2.) Maximize $Z=x_1+x_2$
subject to : $x_1+x_2 \leq 1 \\ x_1+x_2 \leq 1 \\ -x_1+x_2 \leq 1$
and $x_1, x_2 \geq 0$
उत्तर (Answers):(1.) max $Z=50, x_1=5, x_2=0,x_3=0$ ,Max. Z=50
(2.)अपरिबद्ध (unbounded solution)
उपर्युक्त सवालों को हल करने पर एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method) को ठीक से समझ सकते हैं।

Also Read This Article:- Simple Arithmetic Mean and Quartile

4.एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (Frequently Asked Questions Related to How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.सिम्पलेक्स विधि की अभिकलनी प्रक्रिया क्या है? (What is Computational Procedure of Simplex Method?):

उत्तर:सिम्पलेक्स विधि द्वारा किसी दी गई रैखिक प्रोग्रामन समस्या के निम्न चरण हैं:
(1.)समस्या को अधिकतमीकरण की समस्या में बदलना (conversion of the problem into that of maximization)
(2.)b के सभी घटकों को धनात्मक बनाना (To make all the b’s positive)
(4.)आवश्यकतानुसार कृत्रिम चरों का समावेश करना (To introduce artificial variable if needed)
(5.)प्रारम्भिक सारणी तैयार करना (To prepare the initial simplex table)
(6.)इष्टमत्व की जाँच (To test optimality)
(7.)प्रवेशी सदिश का चयन (To fix the entering vector)
(8.)अपगामी सदिश एवं मुख्य अवयव का निर्धारण (To fix up the departing vector and key element)
(9.)नवीन सिम्पलेक्स सारणी को बनाना (To prepare the new simplex table)
(10.)इष्टतम हल प्राप्त न होने पर चरण 6 से 9 की पुनरावृत्ति

प्रश्न:2.समस्या को अधिकतमीकरण की समस्या में कैसे बदलते हैं? (How Do You Convert Problem into that of Maximization?):

उत्तर:यदि दी गई समस्या निम्नतमीकरण (minimization) की समस्या हो तो उसे सर्वप्रथम अधिकतमीकरण (maximization) की समस्या में बदल लेना चाहिए अर्थात् दी गई निम्नतमीकरण की समस्या के दोनों पक्षों को -1 से गुणा कर अधिकतमीकरण की समस्या में बदल लेते हैं।
Min. Z=Max. (-Z)

प्रश्न:3.b के सभी घटकों को धनात्मक कैसे बनाते हैं? (How to Make all the b’s Positive?):

उत्तर:यदि आवश्यकता सदिश b का कोई घटक ऋणात्मक हो तो उसके संगत प्रतिबन्ध को -1 से गुणा कर धनात्मक बना लेते हैं।इससे उस सम्बन्धित प्रतिबन्ध की असमिका $\geq \left ( \leq \right )$ से चिन्ह $\leq \left( \geq \right)$ में बदल जाएगा।
उपर्युक्त प्रश्नों के उत्तर द्वारा एलपीपी को सिम्पलेक्स विधि से कैसे हल करें? (How to Solve LPP with Simplex Method?),रैखिक प्रोग्रामन समस्या को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

How to Solve LPP with Simplex Method?

एलपीपी को सिम्पलेक्स विधि से कैसे हल करें?
(How to Solve LPP with Simplex Method?)