Examples of Complex Integration
1.सम्मिश्र समाकलन के उदाहरण का परिचय (Introduction to Examples of Complex Integration),सम्मिश्र समाकलन (Complex Integration):
सम्मिश्र समाकलन के उदाहरण (Examples of Complex Integration) के इस आर्टिकल में सम्मिश्र समाकलन पर आधारित सवालों को हल करने के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Radius of Convergence Complex Analysis
2.सम्मिश्र समाकलन के उदाहरण (Examples of Complex Integration):
Example:1. \int_{(0,1)}^{(3,10)}[(3 x+y) d x+(2 y-x) d y] का मान
(i)वक्र y=x^2+1
(ii)(0,1) and (3,10) को जोड़ने वाली रेखा साथ ज्ञात करें।
(Evaluate along
(i)the curve y=x^2+1
(ii)The line joining (0,1) and (3,10).)
Solution:(i).वक्र y=x^2+1 के अनुदिश dy=2xdx
x का मान 0 से 3 तक परिवर्तित होता है
\therefore \int_{(0,1)}^{(3,10)}[(3 x+y) d x+(2 y-x) d y] \\ \Rightarrow \int_0^3\left[\left(3 x+x^2 +1 \right) d x+\left(2 x^2+2-x\right) 2 x d x\right] \\ \Rightarrow \int_0^3\left(3 x+x^2+1+4 x^3+4 x-2 x^2 \right) d x \\ \Rightarrow \int_0^3\left(4 x^3-x^2+7 x+1\right) d x \\ \Rightarrow \left[\frac{4 x^4}{4}-\frac{x^3}{3}+\frac{7 x^2}{2}+x\right]_0^3 \\ =3^4-\frac{3^3}{3}+\frac{7}{2} \times 3^2+3 \\ =\frac{81}{1}-\frac{9}{1}+\frac{63}{2}+\frac{3}{1} \\ =\frac{162-18+63+6}{2} \\=\frac{213}{2}
(ii).(0,1) तथा (3,10) को जोड़ने वाली रेखा का समीकरण
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \\ \Rightarrow y-1 =\frac{(0-1)}{3-0}(x-0) \\ \Rightarrow y-1=3(x) \\ \Rightarrow y=3 x+1 \\ \Rightarrow d y=3 d x \\ \therefore \int_{(0,1)}^{(3,10)}[(3 x+y) d x+(2 y-x) d y] \\ =\int_0^3[(3 x+3 x+1) d x+(6 x+2-x) 3 d x] \\ =\int_0^3(6 x+1+15 x+6) d x \\ =\int_0^3(21 x+7) d x \\ =\left[\frac{21 x^2}{2}+7 x\right]_0^3 \\ =\frac{21}{2}(3)^2+7 \times 3 \\ =\frac{189}{2}+\frac{21}{1} \\ =\frac{189+42}{2}= \frac{231}{2}
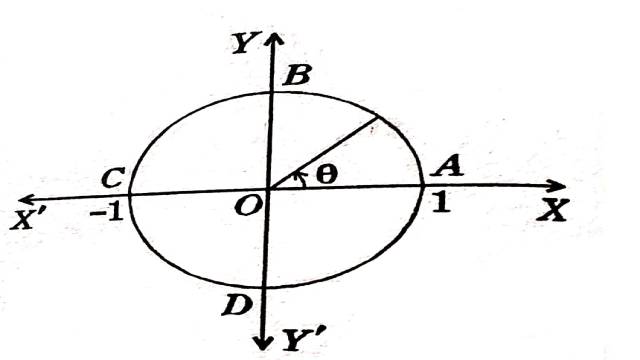
Example:2.दर्शाइए कि -1 से 1 तक अर्धवृत्ताकार चाप |z|=1 के अनुदिश \bar{z} के समाकलन का मान -\pi i या \pi i है,क्योंकि चाप वास्तविक अक्ष के ऊपर या नीचे स्थित है।
(Show that the integral of \bar{z} along a semi-circular arc from -1 to 1 has the value -\pi i or \pi i according as the arc lies above or below the real axis.)
Solution:वृत्त |z|=1 का प्राचलिक समीकरण है:
z=e^{i \theta} जहाँ 0 \leq \theta \leq 2 \pi \\ \Rightarrow dz=i e^{i \theta} d \theta तथा \bar{z}=e^{-i \theta}
चूँकि z वास्तविक अक्ष के ऊपर अर्धवृत्तीय चाप के अनुदिश -1 से 1 की ओर गति करता है, \theta, \pi से 0 तक परिवर्तित होता है:
\therefore \int_{\operatorname{CBA}} \bar{z} d z=\int_\pi^0 e^{-i \theta} i e^{i \theta} d \theta \\ =i \int_{\pi}^0 d \theta=-\pi i
पुनः जब z वास्तविक अक्ष के नीचे अर्धवृत्तीय चाप के अनुदिश -1 से 1 की ओर गति करता है, \theta, \pi से 2 \pi तक परिवर्तित होता है।
\therefore \int_{CDA} \bar{z} d z =\int_\pi^{2 \pi} e^{-i \theta} i e^{i \theta} d \theta \\ =i \int_\pi^{2 \pi} d \theta=\pi i
वृत्त |z|=1 के चारों ओर \bar{z} का समाकल:
\int_{ABCD} \bar{z} d x=\int_{ABC} \bar{z} d z+\int_{CDA} \bar{z} d z \\ =-\int_{CBA} \bar{z} d z+\int_{CDA} z dz=2 \pi i
Example:3. I=\int_{(0,1)}^{(2,5)}(3 x+y) d x+(2 y-x) d y का मान ज्ञात कीजिए
(i)वक्र y=x^2+1
(ii)(0,1) और (2,5) को जोड़ने वाली रेखा
(iii).(0,1) से (0,5) रेखा और फिर (0,5) से (2,5) तक,के अनुदिश।
(Evaluate along I=\int_{(0,1)}^{(2,5)}(3 x+y) d x+(2 y-x) d y
(i).The curve y=x^2+1
(ii)The line joining (0,1) and (2,5)
(iii).The line from (0,1) to (0,5) and then from (0,5) to (2,5).)
Solution:(i) y=x^2+1 तथा d y=2x d x \\ \therefore I=\int_0^2(3 x+y) d x+(2y-x) d y \\ =\int_0^2\left(3 x+x^2+1\right) d x+\left(2 x^2+2-x\right) 2x dx \\ =\int_0^2\left(3 x+x^2+1+4 x^3+4 x-2 x^2\right) dx\\ =\int_0^2\left(4 x^3-x^2+7x+1\right) d x \\ =\left[x^4 -\frac{x^3}{3}+\frac{7 x^2}{2}+x\right]_0^2 \\ =2^4-\frac{2^3}{3}+\frac{7}{2} \times 2^2+2 \\ =\frac{16}{1}-\frac{8}{3}+\frac{14}{1}+\frac{2}{1} \\ =\frac{48-8+42+6}{3}=\frac{88}{3}
(ii).(0,1) तथा (2,5) को जोड़ने वाली रेखा का समीकरण:
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \\ \Rightarrow y-1 =\frac{5-1}{2-0}(x-0) \\ \Rightarrow y-1=\frac{4}{2}(x) \\ \Rightarrow y=2 x+1
तथा dy=2 d x \\ I=\int_0^2[(3 x+y) d x+(2 y-x) d y] \\ =\int_0^2(3 x+2 x+1) d x+(4 x+2-x) 2 d x \\ =\int_0^2(3 x+2 x+1+8 x+4-2 x) d x \\ =\int_0^2(11 x+5) d x \\ =\left[\frac{11x^2}{2}+5 x\right]_0^2 \\ =\frac{11}{2} \times 2^2+5 \times 2=22+10=32
(iii)(0,1) से (0,5) के अनुदिश
जब x=0 तो y,1 से 5 तक परिवर्तित होता है तथा रेखा का समीकरण x=0 है और dx=0
I=\int_1^5[(3 x+y) d x+(2 y-x) d y] \\ =\int_1^5(3 \times 0+y)(0)+(2 y-0) d y \\ =\int_1^5 2 y dy \\=\left[y^2\right]_1^5 =5^2-1^2=24
(0,5) से (2,5) के अनुदिश y=5 और dy=0 तथा x,0 से 2 तक परिवर्तित होता है।
\therefore I=\int_0^2[3 x+y) d x+(2 y-x) d y] \\ =\int_0^2(3 x+5) d x+(2 \times 5-x)(0) \\ =\int_0^2(3 x+5) d x \\=\left[\frac{3 x^2}{2}+5 x\right]_0^2 \\=\frac{3}{2} \times 2^2+5 \times 2 \\ =6+10=16
अतः दिया गया समाकल रेखा (0,1) से (0,5) तथा (0,5) से (2,5) के अनुदिश
=24+16=40
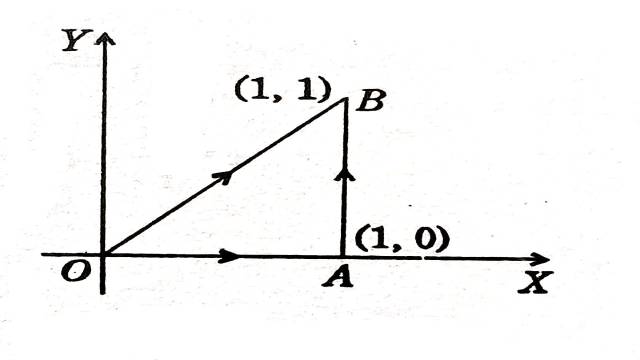
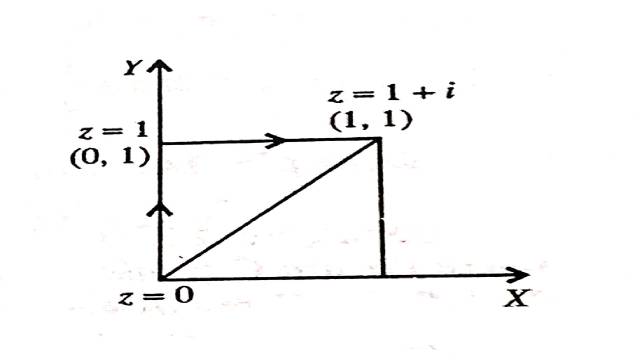
Example:4.समाकल का मान ज्ञात कीजिए
\int_0^{1+i}\left(x-y+i x^2\right) dz
(i) सरल रेखा z=0 से z=1+i के अनुदिश।
(ii) वास्तविक अक्ष के अनुदिश z = 0 से z = 1 तक और फिर काल्पनिक अक्ष के समानांतर एक रेखा के अनुदिश z=1 से z = 1+i तक
(Find the value of the integral \int_0^{1+i}\left(x-y+i x^2\right) dz
(i) Along the straight line from z=0 to z=1+i.
(ii) Along the real axis from z=0 to z=1 and then along a line parallel to the imaginary axis from z=1 to z=1+i.)
Solution: z=x+iy \Rightarrow dz=dx+idy
मान लीजिए कि आर्गैन्ड तल में अनुलग्न (affix) 1 का बिंदु A और अनुलग्न (affix) 1+i का बिंदु B है।OB और AB को मिलाया।
(i).OB,z=0 से z=1+i को जोड़ने वाली सीधी रेखा है।
जाहिर है OB पर, हम y = x लेते हैं
\therefore dy=dx \\ \int_{0 B}\left(x-y+a^2\right) d z=\int_0^1\left(x-x+i x^2\right)(1+i) d x \\ =\int_0^1 i(1+i) x^2 d x=(-1+i)\left[\frac{1}{3} x^3\right]_0^1 \\ =\frac{1}{3}(-1+i)
(ii) OA वास्तविक अक्ष के समानांतर z = 0 से z = 1 तक की रेखा है और AB काल्पनिक अक्ष के समानांतर z=1 से z=1 + i तक की रेखा है।रेखा OA पर,y = 0
z=x+iy तथा dz=dx
\therefore z=x+i y=x तथा d z=d x \\ \therefore \int_{0 A}\left(x-y+i x^2\right) d z \\ =\int_0^1\left(x+i x^2\right) d x \\ =\left[\frac{x^2}{2}+\frac{i x^3}{3}\right]_0^1 \\=\frac{1}{2}+\frac{i}{3}
AB रेखा पर, x=1, \therefore z=1+i y \Rightarrow dz=i dy \\ \int_{A B}\left(x-y+i x^2\right) d z= \int_0^1(1+i-y) d y \\ =i\left[(1+i) y-\frac{y^2}{2}\right]_0^1 \\ =-1+\frac{i}{2} \\ \int_0^{1+i}\left(x-y+i x^2\right) dz कन्टूर OAB के अनुदिश
=\int_{O A}\left(x-y+i x^2\right) d z+\int_{A B}\left(x-y+i x^2\right) d z \\ =\frac{1}{2}+\frac{i}{3}-1+\frac{i}{2} \\ =-\frac{1}{2}+\frac{5}{6} i
Example:5.वृत्त |z|=2 के अनुदिश \int_C\left(z^2+3 z\right) dz का मान ज्ञात करें (2,0) से (0,2) तक
(Evaluate \int_C\left(z^2+3 z\right) dz along the circle |z|=2 from (2,0) to (0,2).)
Solution: z=x+i y \Rightarrow d z=d x+i d y \\ |z|=2 \Rightarrow \sqrt{x^2+y^2}=2 \\ \Rightarrow x^2+y^2=4
Put x=2 \cos t, y=2 \sin t
\theta, 0 से \frac{\pi}{2} तक परिवर्तित होता है।
\therefore d x=-2 \sin t d t, d y=2 \cos t dt \\ z=2(\cot t+i \sin t)=2 e^{i t} \\ dz=(-2 \sin t+2 \cos t) d t \\ \Rightarrow d z =2 e^{i\left(\frac{\pi}{2}+i\right)} dt \\ \int_c\left(z^2+3 z\right) d z= \int_0^{\frac{\pi}{2}} \left[\left(2 e^{i t}\right)^2+3 \cdot 2 e^{i t}\right] z e^{i(\frac{\pi}{2}+t)} dt \\=2 \int_0^{\frac{\pi}{2}} \left(4 e^{2 i t}+6 e^{i t}\right) e^{i\left(\frac{\pi}{2}+t\right)} d t \\ =8 \int_0^{\frac{\pi}{2}} e^{i\left( \frac{\pi}{2}+3 t\right)} d t+12 \int_0^{\frac{\pi}{2}} e^{i\left(\frac{\pi}{2}+2 t\right)} dt \\ =\left[8 \frac{e^{i\left(\frac{\pi}{2}+3 t\right)}}{3 i}+12 \frac{e^{i\left(\frac{\pi}{2}+2 i\right)}}{2 i}\right]_0^{\frac{\pi}{2}} \\ =\frac{8}{3 i}\left(e^{2 \pi i}-e^{\frac{\pi i}{2}}\right)+\frac{12}{2 i}\left(e^{\frac{3 \pi i}{2}}-e^{\frac{i \pi}{2}}\right) \\ =\frac{8}{3 i}(1-i)+\frac{6}{i}(-1-i) \\=\frac{8}{3 i}-\frac{8}{3}-12 \\=-\frac{8 i}{3}-\frac{44}{3} \\ =-\left(\frac{44}{3}+\frac{8 i}{3}\right)
Example:6. \int_C f(z) dz का मान ज्ञात कीजिए जहाँ f(z)=y-x-3 x^2 i और C
(i) z = 0 से z = 1+i तक रेखाखंड है।
(ii) दो रेखाखंडों से मिलकर बनता है,एक z=0 से z=i तक और दूसरा z=i से z=1+i तक।
(Evaluate \int_C f(z) d z Where f(z)=y-x-3 x^2 i and C
(i) is the line segment from z=0 to z=1+i
(ii)consists of two line segments,one from z=0 to z=i and the other from z=i to z=1+i.)
Solution: f(z)=y-x-3 x^2 i
(i).z=0 तथा z=1+i को जोड़ने वाली रेखा का समीकरण y=x है
\therefore d y=d x \\ \therefore dz=(1+i) dx तथा x, 0 से 1 तक परिवर्तित होता है।
\therefore \int_C f(z) d z=\int_0^1 -3 x^2i(1+i) d y \\ =-i(1+i)[x^3]_0^1 \\ =-i(1+i) =1-i
(ii).रेखा z=0 से z=i के अनुदिश
x=0,y, 0 से 1 तक परिवर्तित होता है।
\therefore dx=0 तथा dz=i d y \\ \therefore \int_C f(z) d z=\int_0^1 y i dy \\ =i\left[\frac{y^2}{2}\right]_0^1=\frac{i}{2}
रेखा z=i से z=1+i के अनुदिश,y=0 तथा x,0 से 1 तक परिवर्तित होता है।
\therefore dy=0 तथा dz=dx \\ \therefore \int_c f(z) d z=\int_0^1\left(1-x-3 x^2 i\right) dx \\ =\left[x-\frac{x^2}{2}-x^3 i\right]_0^1 \\=\frac{1}{2}-i \\ \Rightarrow \int_C f(z) d z=\frac{i}{2}+\frac{1}{2}-i=\frac{1-i}{2}
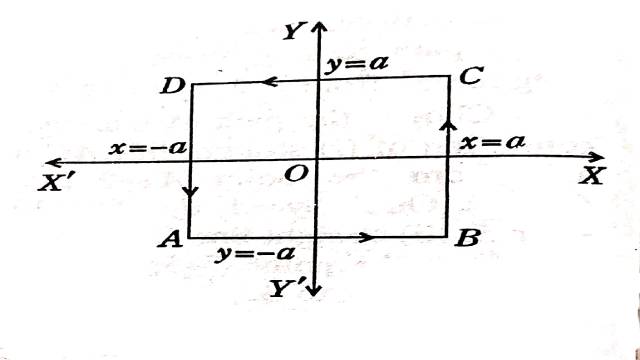
Example:7. \int_L \frac{d z}{L} का मान ज्ञात कीजिए जहाँ L धनात्मक अर्थ में वर्ग को निरूपित करता है जिसकी भुजाएँ अक्षों के समांतर हैं तथा लंबाई 2a है तथा जिसका केंद्र मूल बिंदु पर है।
(Evaluate \int_L \frac{d z}{L} where L represents the square described in the positive sense with sides parallel to the axes and of length 2a and having its centre at the origin.)
Solution:माना ABCD दिया गया वर्ग है जिसका वर्णन धनात्मक अर्थ में किया गया है जिसकी भुजाएँ अक्षों के समानांतर हैं और लंबाई 2a है और जिसका केंद्र मूल बिंदु O पर है।रेखा BC पर,x = a,dx=0 और y,-a से a तक परिवर्तित होता हैं।
रेखा CD पर,y=a,dy= 0 और x,a से -a तक बदलता है।अंत में रेखा DA पर x=-a,dx=0 और y,a से -a तक परिवर्तित होता हैं।
\int_L \frac{d z}{z}=\int_{A B C D} \frac{d z}{z} \\ =\int_{A B} \frac{d z}{z}+\int_{B C} \frac{d z}{z}+\int_{C D} \frac{d z}{z}+\int_{D A} \frac{d z}{z} \\=\int_{-a}^a \frac{d x}{x-i a}+\int_{-a}^a \frac{i d y}{a+i y}+\int_a^{-a} \frac{d x}{x+i a}+\int_a^{-a} \frac{i d y}{-a+i y} \\ =\int_{-a}^a \frac{x+i a}{x^2+a^2} d x+i \int_{-a}^a \frac{a-i y}{a^2+y^2} d y+\int_a^{-a} \frac{x-ia}{x^2+a^2} dx+i \int_a^{-a} \frac{(a+i y)}{a^2+y^2} dy \\ =\left[\frac{1}{2} \log \left(x^2+a^2\right)+i \tan ^{-1} \frac{x}{a}\right]_{-a}^a+i\left[\tan ^{-1} \frac{y}{a}-\frac{i}{2} \log \left(a^2+y^2\right)\right]_{-a}^a +\left[\frac{1}{2} \log \left(x^2+a^2 \right)-i \tan ^{-1} \frac{x}{a}\right]_a^{-a}+i\left[\tan ^{-1} \frac{y}{a}+\frac{i}{2} \log \left(a^2+y^2 \right)\right]_a^{-a} \\ =2 \pi i
Example:8. \int_L \frac{z+2}{z} d z का मान ज्ञात कीजिए जहाँ L अर्धवृत्त z=2 e^{it}, 0 \leq t \leq \pi है।
(Evaluate \int_L \frac{z+2}{z} d z where L is the semi-circle z=2 e^{it}, 0 \leq t \leq \pi .)
Solution: z=2 e^{i t}, 0 \leq t \leq \pi\\ dz=2 i e^{i t} d t \\ \int_L \frac{z+2}{2} d z=\int_0^\pi \frac{\left(2 e^{i t}+2\right)}{2 e^{i t}} 2 i e^{i t} d t \\ =2 i \int_0^\pi\left(1+\bar{e}^{i t}\right) e^{i t} d t \\ =2 i \int_0^\pi\left(e^{i t}+1\right) dt \\ =2 i\left[\frac{e^{i t}}{i}+t\right]_0^\pi=2 i\left(\frac{e^{i \pi}}{i}-\frac{1}{i}+\pi\right) \\ =2 e^{i \pi}-2+2 i \pi=-4+2 i \pi
उपर्युक्त उदाहरणों के द्वारा सम्मिश्र समाकलन के उदाहरण (Examples of Complex Integration),सम्मिश्र समाकलन (Complex Integration) को समझ सकते हैं।
Also Read This Article:- Bilinear Transformations
3.सम्मिश्र समाकलन के उदाहरण (Frequently Asked Questions Related to Examples of Complex Integration),सम्मिश्र समाकलन (Complex Integration) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.नियमित चाप किसे कहते हैं? (What is a Regular Arc?):
उत्तर:यदि समीकरण z=z(t)=x(t)+iy(t) द्वारा वर्णित बिन्दु z एक जोरदाँ वक्र पर तथा एकमानीय हो एवं संवृत्त अन्तराल [\alpha, \beta] में स्थित t के सभी मानों के लिए x(t),y(t) तथा x'(t),y'(t) संतत फलन हो तो चाप को जोरदाँ वक्र का नियमित चाप (regular arc) कहते हैं।
प्रश्न:2.संवृत्त कन्टूर किसे कहते हैं? (What is a Closed Contour?):
उत्तर:यदि कंटूर संवृत्त हो अर्थात् \alpha एवं \beta के मानों के लिए संगत बिन्दु सम्पाती हो तथा स्वयं के साथ प्रतिच्छेद न करता हो तो यह खण्डशः निष्कोण वक्र (piecewise smooth curve) होगा जिसे संवृत्त कन्टूर (closed contour) कहते हैं।
प्रश्न:3.पारकाट से क्या आशय है? (What Do You Mean by Cross Cut?):
उत्तर:बहुसम्बन्धित प्रदेश में खींची गई वे रेखाएँ पारकाट (cross cut) कहलाती हैं जो किसी भी वक्र को न काटे और इस बहुसम्बन्धित प्रदेश को एकशः सम्बन्धित प्रदेश में परिवर्तित कर दें।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्मिश्र समाकलन के उदाहरण (Examples of Complex Integration),सम्मिश्र समाकलन (Complex Integration) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Examples of Complex Integration
सम्मिश्र समाकलन के उदाहरण
(Examples of Complex Integration)
Examples of Complex Integration
सम्मिश्र समाकलन के उदाहरण (Examples of Complex Integration) के इस आर्टिकल
में सम्मिश्र समाकलन पर आधारित सवालों को हल करने के बारे में अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.