Examples of Area of Parallelogram 9th
1.समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण का परिचय (Introduction to Examples of Area of Parallelogram 9th),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelogram and Triangles Class 9):
समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Examples of Area of Parallelogram 9th) के इस आर्टिकल में समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल पर आधारित सवालों को हल करने के बारे में अध्ययन करेंगे और समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Parallelogram Class 9th
2.समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Examples of Area of Parallelogram 9th):
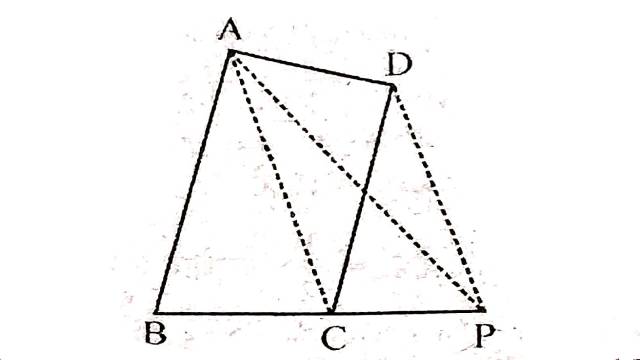
Example:1 ABCD एक चतुर्भुज है।D से होकर AC के समान्तर खींची गई एक रेखा खींची गई जो BC को बढ़ाने पर P पर मिलती है।सिद्ध कीजिए कि:
ar(\triangle ABP)=ar(चतुर्भुज ABCD)
Solution:दिया है (Given):ABCD एक चतुर्भुज है।AC के समान्तर एक रेखा D से होकर खींची गई है जो BC को P पर मिलती है।
सिद्ध करना है (To Prove): ar(\triangle ABP)=ar(चतुर्भुज ABCD)
उपपत्ति (Proof): DP \| AC (दिया है)
\because \triangle ACP और \triangle ACD एक ही समान्तर रेखाओं AC और DP के बीच और एक ही आधार AC पर स्थित हैं।
\therefore ar(\triangle ACP)=ar(\triangle ACD)
दोनों पक्षों में ar(\triangle ABC) जोड़ने पर:
ar(\triangle ACP)+ar(\triangle ABC)=ar(\triangle ACD)+ar(\triangle ABC) \\ \Rightarrow ar(\triangle ABP)=ar(\text{ चतुर्भुज } ABCD)
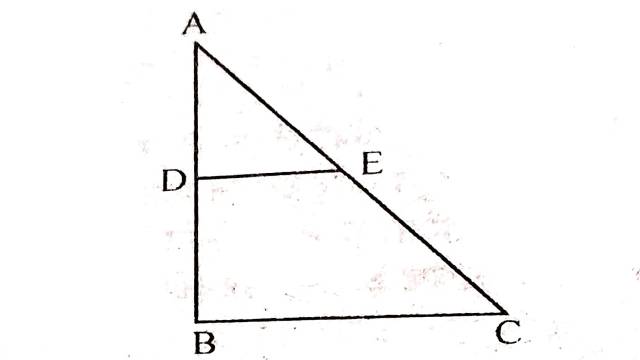
Example:2.आकृति में, DE=\frac{3}{4} BC, DE \| BC और DE तथा BC के बीच की दूरी 3 इकाई है।यदि BC 6 इकाई हो,तो DBCE का क्षेत्रफल ज्ञात करो।
Solution:चतुर्भुज DBCE में DE \| BC
अतः DBCE समलम्ब चतुर्भुज है।
समलम्ब चतुर्भुज DBCE का क्षेत्रफल
=\frac{1}{2} \times(DE+BC) \times \text{समान्तर भुजाओं के बीच दूरी} \\ =\frac{1}{2} \times \left(\frac{3}{4} B C+BC\right) \times 3\left[\because BC=\frac{3}{4} BC\right] \\ = \frac{1}{2} \times\left(\frac{3}{4} \times 6+6\right) \times 3\left[ \because BC=6 \text { इकाई } \right] \\ =\frac{1}{2} \times\left(\frac{9+12}{2}\right) \times 3 \\ =\frac{1}{2} \times \frac{21}{2} \times 3 \\ =\frac{63}{4}
=15.75 वर्ग इकाई
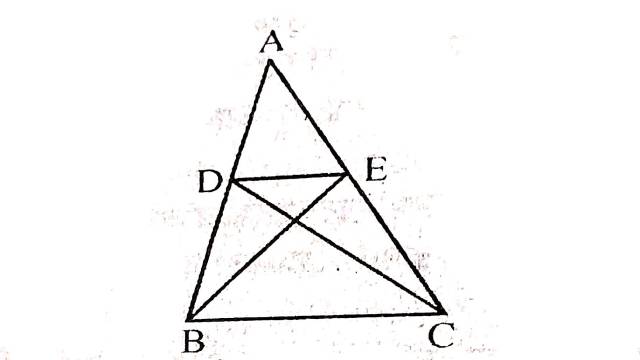
Example:3.आकृति में, \triangle ABC की भुजाओं AB और AC पर बिन्दु D और E इस प्रकार स्थित हैं कि ar(\triangle BCE)=ar(\triangle BCD) है।सिद्ध करो कि DE \| BC
Solution:दिया है (Given):बिन्दु D और E, \triangle ABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि:
ar(\triangle BCE)=ar(\triangle BCD)
सिद्ध करना है (To Prove): DE \| BC
उपपत्ति (Proof): ar(\triangle BCE)=ar(\triangle BCD) (दिया है)
और \triangle BCE तथा \triangle BCD एक ही आधार BC पर स्थित हैं।
चूँकि दोनों त्रिभुज एक ही आधार और समान रेखाओं DE व BC के बीच स्थित हैं तथा उनके क्षेत्रफल समान हैं।
\therefore \triangle BCE और \triangle BCD एक ही समान्तर रेखाओं के बीच स्थित हैं।
अतः DE \| BC
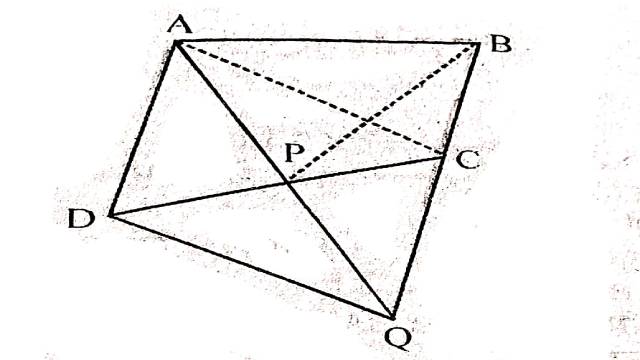
Example:4.आकृति,में ABCD एक समान्तर चतुर्भुज है।सिद्ध कीजिए कि
ar(\triangle BCP)=ar(\triangle DPQ)
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है और BC को Q तक इस प्रकार बढ़ाया गया है कि AD=CQ है।QD और AQ को मिलाया गया है।
सिद्ध करना है (To Prove): ar(\triangle BCP)=ar(\triangle DPQ)
रचना (Construction):AC और PB को मिलाया।
उपपत्ति (Proof):चतुर्भुज ADQC में
\because AD=CQ और AD \| CQ (दिया है)
\therefore ADQC एक समान्तर चतुर्भुज है।
[चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समान्तर है]
\because \triangle DQC और \triangle AQC एक ही आधार QC और एक ही समान्तर रेखाओं AD \| CQ के बीच स्थित हैं।
\therefore ar(\triangle DQC)=ar(\triangle AQC) \cdots(1)
दोनों पक्षों में ar(\triangle PQC) घटाने पर:
ar(\triangle DQC)-ar(\triangle PQC)=ar(\triangle AQC) -ar(\triangle PQC) \\ \Rightarrow ar(\triangle DPQ)=ar(\triangle APC) \cdots(2)
\triangle APC और \triangle BCP एक ही आधार PC तथा एक ही समान्तर रेखाओं AB और PC के बीच स्थित हैं अतः
ar(\triangle APC)=ar(\triangle BCP) \cdots(3)
(2) व (3) से:
ar(\triangle DPQ)=ar(\triangle BCP)
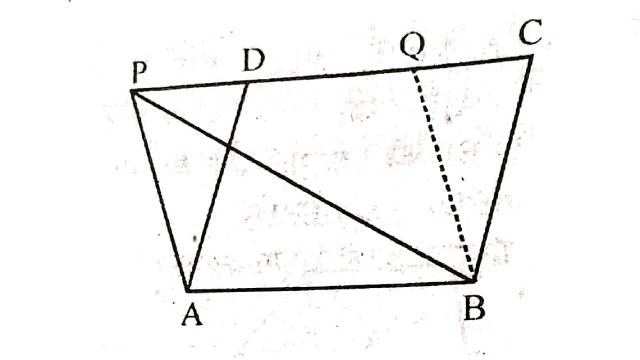
Example:5.एक समान्तर चतुर्भुज ABCD की एक भुजा AB को P तक बढ़ाया गया है।A से होकर एक रेखा CP के समान्तर खींची गई है जो CB को बढ़ाने पर Q पर मिलती है और समान्तर चतुर्भुज PBQR बनता है,जैसा कि आकृति में दर्शाया गया है।सिद्ध कीजिए कि:
ar (समान्तर चतुर्भुज ABCD)=ar (समान्तर चतुर्भुज BPRQ)
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD की भुजा AB को P तक बढ़ाया है।A से होकर एक रेखा CP के समान्तर है जो CB को बढ़ाने पर Q पर मिलती है और PBQR एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):ar(समान्तर चतुर्भुज ABCD)=ar(समान्तर चतुर्भुज BPRQ)
रचना (Construction):AC और PQ को मिलाया।
उपपत्ति (Proof): \triangle AQC और \triangle AQP एक ही आधार AQ पर और एक ही समान्तर रेखाओं CP और AQ के बीच स्थित हैं।
\therefore ar(\triangle AQC)=ar(\triangle AQP) \cdots(1)
\Rightarrow दोनों पक्षों में ar(\triangle ABQ) घटाने पर:
ar(\triangle AQC)-ar(\triangle ABQ)=ar(\triangle AQP)-ar(\triangle ABQ) \\ \Rightarrow ar(\triangle ABC)=ar(\triangle BQP) \\ \Rightarrow 2 \times \operatorname{ar}(\triangle ABC)=2 \times \operatorname{ar}(\triangle BQP) \cdots(2)
\because AC,समान्तर चतुर्भुज ABCD का एक विकर्ण है।
\therefore 2 \times \operatorname{ar}(\triangle ABC)= \operatorname{ar} \text{ (समान्तर चतुर्भुज ABCD) } \cdots(3)
इसी प्रकार 2 \times \operatorname{ar}(\triangle BQP)= \operatorname{ar} \text{ (समान्तर चतुर्भुज BPRQ)} \cdots(4)
(2),(3) और (4) से:
ar (समान्तर चतुर्भुज ABCD)=ar (समान्तर चतुर्भुज BPRQ)
Example:6.यदि एक त्रिभुज और एक समान्तर चतुर्भुज एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हों,तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल समान्तर चतुर्भुज के क्षेत्रफल का आधा होता है।
Solution:दिया है (Given): \triangle ABP और समान्तर चतुर्भुज ABCD एक ही आधार AB और एक ही समान्तर रेखाओं AB और PC के बीज स्थित हैं।
सिद्ध करना है (To Prove): \operatorname{ar}(PAB)=\frac{1}{2} \operatorname{ar}(ABCD)
रचना (Construction):एक अन्य समान्तर चतुर्भुज ABQP प्राप्त करने के लिए, BQ \| AP खींची।
उपपत्ति (Proof):समान्तर चतुर्भुज ABQP और ABCD एक ही आधार AB और एक ही समान्तर रेखाओं AB और PC के बीच स्थित हैं।
अतः ar(ABQP)=ar(ABCD) ….. (1)
परन्तु \triangle PAB \cong \triangle BQP (विकर्ण PB समान्तर चतुर्भुज ABQP को दो सर्वांगसम त्रिभुजों में बाँटता है)
अतः ar(PAB)=ar(BQP) …….(2)
इसलिए, ar(PAB)=\frac{1}{2} ar(ABQP) [(2) से]
अतः [(1) व (2) से]
ar(PAB)=\frac{1}{2} \operatorname{ar}(ABCD)
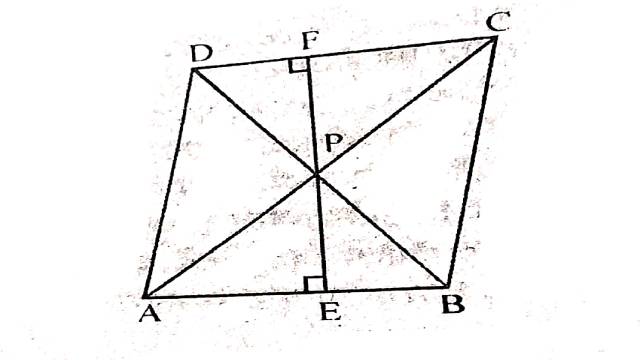
Example:7.समान्तर चतुर्भुज ABCD के अभ्यन्तर में P एक बिन्दु है।सिद्ध कीजिए कि:
\operatorname{ar}(\triangle ABP)+\operatorname{ar} (\triangle DCP)= \frac{1}{2} \operatorname{ar} \text{(समान्तर चतुर्भुज ABCD)}
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है।इसके अभ्यन्तर में P एक बिन्दु है।
सिद्ध करना है (To Prove): \operatorname{ar}(\triangle ABP)+\operatorname{ar} (\triangle DCP)=\frac{1}{2} \operatorname{ar} \text{(समान्तर चतुर्भुज ABCD)}
रचना (Construction): PE \perp AB और PF \perp CD खींचा
उपपत्ति (Proof): \operatorname{ar}(\triangle ABP)=\frac{1}{2} \times AB \times PE \cdots(1)
और \operatorname{ar}(\triangle DCP) =\frac{1}{2} \times CD \times PF \\=\frac{1}{2} \times AB \times PF \cdots(2)
( \because CD=AB,समान्तर चतुर्भुज की सम्मुख भुजाएँ)
(1) व (2) को जोड़ने पर:
\operatorname{ar}(\triangle ABP)+\operatorname{ar} (\triangle DCP)=\frac{1}{2} AB \times PE+\frac{1}{2} \times AB \times PF \\ =\frac{1}{2} A B(P E+P F) \\ =\frac{1}{2} \times A B \times EF \\ \Rightarrow \operatorname{ar}(\triangle ABP)+\operatorname{ar} (\triangle DCP)= \frac{1}{2} \operatorname{ar} \text{(समान्तर चतुर्भुज ABCD)}
उपर्युक्त उदाहरणों के द्वारा समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Examples of Area of Parallelogram 9th),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelogram and Triangles Class 9) को समझ सकते हैं।
3.समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण पर आधारित सवाल (Questions Based on Examples of Area of Parallelogram 9th):
(1.)दो त्रिभुज एक ही आधार एवं एक ही समान्तर रेखाओं के मध्य स्थित हैं।एक त्रिभुज की ऊँचाई 5 सेमी तथा क्षेत्रफल 18 वर्गसेमी है।दूसरे त्रिभुज की ऊँचाई बताइए।
(2.)एक त्रिभुज व एक स. च. का आधार 16 सेमी है।दोनों एक ही समान्तर रेखाओं के मध्य स्थित हैं।त्रिभुज का क्षेत्रफल ज्ञात कीजिए।यदि स. च. की ऊँचाई 12 सेमी है।
उत्तर (Answers):(1.)5 सेमी (2.)96 वर्गसेमी
उपर्युक्त सवालों को हल करने पर समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Examples of Area of Parallelogram 9th),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelogram and Triangles Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:- Illustrations of Congruent Triangles
4.समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Frequently Asked Questions Related to Examples of Area of Parallelogram 9th),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelogram and Triangles Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.समतलीय आकृतियों का क्षेत्रफल ज्ञात करने की आवश्यकता क्यों महसूस हुई? (Why Was There a Need to Find the Area of Planner Figures?):
उत्तर:कार्तिक अपने एक समलम्ब आकृति के खेत का बँटवारा अपनी दो पुत्रियों को असमान्तर सीमाओं के मध्य बिन्दुओं से लकीर खींच कर करता है।क्या यह बँटवारा क्षेत्रफल में समान हुआ है? इस प्रकार की समस्याओं के समाधान के लिए यह आवश्यक है कि समतलीय आकृतियों के क्षेत्रफल पर चिन्तन किया जाए।
प्रश्न:2.क्षेत्रफल को परिभाषित कीजिए। (Define the Area):
उत्तर:एक सरल बन्द आकृति द्वारा किसी तल पर घेरा हुआ भाग उस आकृति का तलीय क्षेत्र कहलाता है और इस तलीय क्षेत्र का परिमाण या माप उस आकृति का क्षेत्रफल (area) कहलाता है।
प्रश्न:3.क्या क्षेत्रफल में समान आकृतियाँ सर्वांगसम होती हैं? (Are the Same Shapes Congruent in the Area?):
उत्तर:सर्वांगसम आकृतियाँ क्षेत्रफल में समान होती हैं परन्तु क्षेत्रफल में समान आकृतियाँ सर्वांगसम भी हों,यह आवश्यक नहीं।
उपर्युक्त प्रश्नों के उत्तर द्वारा समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Examples of Area of Parallelogram 9th),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelogram and Triangles Class 9) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Examples of Area of Parallelogram 9th
समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण
(Examples of Area of Parallelogram 9th)
Examples of Area of Parallelogram 9th
समान्तर चतुर्भुजों के क्षेत्रफल 9वीं के उदाहरण (Examples of Area of Parallelogram 9th)
के इस आर्टिकल में समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल पर आधारित सवालों को हल
करने के बारे में अध्ययन करेंगे और समझेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.