Evaluation of Contour Integration
1.परिरेखा समाकलन का मूल्यांकन (Evaluation of Contour Integration),परिरेखा समाकलन (Contour Integration):
परिरेखा समाकलन का मूल्यांकन (Evaluation of Contour Integration) के इस आर्टिकल में परिरेखा समाकलन पर आधारित विशिष्ट सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Examples of Contour Integration
2.परिरेखा समाकलन का मूल्यांकन के साधित उदाहरण (Evaluation of Contour Integration Solved Illustrations):
Illustration:1.सिद्ध करो कि (Prove that)
\int_{-\infty}^{\infty} \frac{\sin x}{x^2+4 x+5} d x=-\frac{\pi}{e} \sin 2
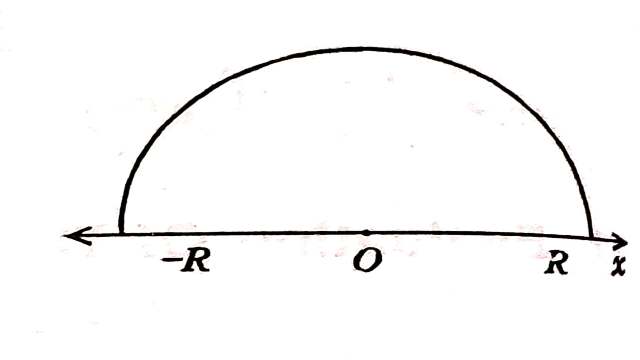
Solution:समाकल \int_c \frac{e^{iz}}{z^2+4 z+5} d z=\int_c f(z) d z पर विचार करें,जहाँ C परिरेखा है।
z^2+4 z+5=0 \Rightarrow z=-2 \pm i
इस प्रकार z=-2+i=\alpha,-2-i=\beta, f(z) के साधारण अनन्तक हैं।
इनमें से केवल z=\alpha ,C के अन्दर स्थित हैं।
z=\alpha पर अवशेष
\underset{z \rightarrow \alpha}{\lim} (z-\alpha) f(z) \\ =\underset{z \rightarrow \alpha}{\lim} \frac{e^{i z}(z-\alpha)}{(z-\alpha)(z-\beta)}=\underset{z \rightarrow \alpha}{\lim} \frac{e^{i z}}{z-\beta} \\ =\frac{e^{i \alpha}}{\alpha-\beta}=\frac{e^{i(-2+i)}}{2 i}=\frac{e^{-2 i} \cdot e^{-1}}{2 i}
कोशी अवशेष प्रमेय से:
\int_C f(z) d z=\int_{-R}^R \frac{e^{i x}}{x^2+4 x+5} d x+\int_{\Gamma} \frac{e^{i z}}{z^2+4 z+5} d z=2 \pi i \Sigma R^{+} \\ \underset{z \rightarrow \infty}{\lim} \frac{1}{z^2+4 z+5}=0 (जोरदाँ उपप्रमेय से)
\underset{R \rightarrow \infty}{\lim} \int_{\Gamma} f(z) d z=0 \\ \therefore \underset{R \rightarrow \infty}{\lim} \int_{-R}^R \frac{e^{i x}}{x^2+4 x+5} d x=2 \pi i \Sigma R^{+} \\ \int_{-\infty}^{\infty} \frac{e^{i x}}{x^2+4 x+5} d x=2 \pi i \cdot \frac{e^{-2 i} \cdot e^{-1}}{2 i}=\frac{\pi}{e} e^{2 i}
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{\sin x}{x^2+4 x+5} d x=-\frac{\pi}{e} \sin 2
Illustration:2.सिद्ध करो कि (Show that)
\int_{-\infty}^{\infty} \frac{\sin x}{x^2-2 x+5} d x=\frac{\pi}{2 e^2} \sin 1
Solution: \int_c \frac{e^{i z}}{z^2-2 z+5} d z=\int_c f(z) d z पर विचार करें,जहाँ C परिरेखा है।
z^2-2 z+5=0 \Rightarrow z=\frac{2 \pm \sqrt{(-2)^2-4 \times 1 \times 5}}{2 \times 1} \\ \Rightarrow z=1 \pm 2 i
इस प्रकार z=1+2 i=\alpha, 1-2 i=\beta ,f(z) के साधारण अनन्तक हैं।
इनमें से केवल z=1+2 i=\alpha ,C के अन्दर स्थित है।
z=\alpha पर अवशेष
\underset{z \rightarrow \alpha}{\lim} (z-\alpha) f(z)= \underset{z \rightarrow \infty}{\lim} \frac{e^{i z}(z-\alpha)}{(z-\alpha)(z-\beta)} \\ =\underset{z \rightarrow \alpha}{\lim} \frac{e^{i z}}{z-\beta} \\ =\frac{e^{i \alpha}}{\alpha-\beta}=\frac{e^{i(1+2 i)}}{4 i}=\frac{e^i \cdot e^{-z}}{4 i}
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=\int_{-R}^R \frac{e^{i x}}{x^2-2 x+5} d x+\int_{\Gamma}\frac{e^{iz}}{z^2+4 z+5} d z=2 \pi i \Sigma R^{+}
जबकि \underset{z \rightarrow \infty}{\lim} \frac{1}{z^2-2 z+5}=0 (जोरदाँ उपप्रमेय से)
\underset{R \rightarrow \infty}{\lim} \int_{\Gamma} f(z) d z=0 \\ \therefore \lim _{R \rightarrow \infty} \int_{-R}^{R} \frac{e^{i x}}{x^2-2 x+5} d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{i x}}{x^2-2 x+5} d x=2 \pi i \cdot \frac{e^i e^{-2}}{4 i}=\frac{\pi}{2 e^2} e^i
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{\sin x}{x^2-2 x+5} d x=\frac{\pi}{2 e^2} \sin 1
Illustration:3.समाकलन के द्वारा (By integration) \frac{e^{i z}}{(z-a i)},(a>0) एक उपयुक्त परिरेखा के चारों ओर (round a suitable contour),सिद्ध करो कि (Prove that)
\int_{-\infty}^{\infty} \frac{a \cos x+x \sin x}{x^2+a^2} d x=2 \pi e^{-a}
Solution:समाकल \int_c \frac{e^i z}{z-i a}=\int_c f(z) d z पर विचार करें,जहाँ C परिरेखा है।
z=ia, f(z) का साधारण अनन्तक है जो C के अन्दर स्थित है।
z=ia पर अवशेष
\underset{z \rightarrow i a}{\lim} (z-i a) f(z)=\underset{z \rightarrow i a}{\lim} e^{i z}=e^{-a}
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=\int_{-R}^R \frac{e^{i x}}{x-i a} d x+\int_{\Gamma} \frac{e^{i z}}{z-i a} d z = 2 \pi i \Sigma R^{+}
जोरदाँ उपप्रमेय सेः
\underset{R \rightarrow \infty}{\lim} \int_{\Gamma} \frac{e^{i z}}{z-i a} d z=0 \\ =\underset{R \rightarrow \infty}{\lim} \int_{-R}^R \frac{e^{i x}}{x-i a} d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{i x}}{x-i a} d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{(\cos x+i \sin x)(x+i a)}{(x-i a)(x+i a)} d x=2 \pi i e^{-a} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{x \cos x-a \sin x+i(x \sin x+a \cos x)}{x^2+a^2} d x=i 2 \pi e^{-a}
दोनों पक्षों के काल्पनिक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{x \sin x+a \cos x}{x^2+a^2} d x=2 \pi e^{-a}
Illustration:4.एक उपयुक्त परिरेखा के चारों ओर \frac{e^{i z}}{z+a i} के समाकलन द्वारा,सिद्ध करो कि
(By integrating \frac{e^{i z}}{z+a i} round a suitable contour, prove that)
\int_{-\infty}^{\infty} \frac{-a \cos x+x \sin x}{x^2+a^2} d x=0
Solution: \int_c \frac{e^{i z}}{z+a i}=\int_c, f(z) पर विचार करें,जहाँ C परिरेखा है।
z=-ia, f(z) का साधारण अनन्तक है परन्तु यह वास्तविक अक्ष के ऊपर नहीं है,फलस्वरूप f(z) का कोई अनन्तक नहीं है जो C के अन्दर स्थित है।
कोशी अवशेष प्रमेय सेः
\int_c f(z) d z=\int_{-R}^R \frac{e^{i x}}{x+i a} d x+\int_{\Gamma} \frac{e^{i z}}{z+i a} dx=2 \pi i \Sigma R^{+}
जोरदाँ उपप्रमेय सेः
\underset{z \rightarrow \infty}{\lim} \int_{\Gamma} \frac{e^{i z}}{z+i a} d z=0 \\ \therefore \lim _{R \rightarrow \infty} \int_{-R}^R \frac{e^{i x}}{x+i a} d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{i x}}{x+i a} d x=0 [ C के अन्दर अनन्तक नहीं है]
\Rightarrow \int_{-\infty}^{\infty} \frac{(\cos x+i \sin x)(x-i a)}{(x+i a)(x-i a)}=0
दोनों पक्षों के काल्पनिक भागों की तुलना करने पर:
\int_{-\infty}^{\infty} \frac{x \sin x-a \cos x}{x^2+a^2} d x=0
Illustration:4.मान ज्ञात करो (Evaluate)
\int_0^{\infty} \frac{\cos a x}{\left(x^2+b^2\right)^2} d x, a>0, b>0
Solution: \int_c \frac{e^{(a z}}{\left(z^2+b^2\right)^2} d z=\int_c f(z) d z
पर विचार करें,जहाँ C परिरेखा है।
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=\int_{-R}^R \frac{e^{i a x}}{\left(x^2+b^2\right)^2} d x+\int_{\Gamma} \frac{e^{i a z}}{\left(z^2+b^2\right)^2} dz= 2 \pi i \Sigma R^{+}
जोरदाँ उपप्रमेय सेः
\underset{R \rightarrow \infty}{\lim} \int_{\Gamma} \frac{e^{i a z}}{\left(z^2+b^2\right)^2} d z=0 \\ \therefore \underset{R \rightarrow \infty}{\lim} \int_{-R}^R \frac{e^{i a x}}{\left(x^2+b^2\right)^2} d x=2 \pi i \Sigma R^{+} \\ \int_{-\infty}^{\infty} \frac{e^{i a x}}{\left(x^2+b^2\right)} d x=2 \pi i \Sigma R^{+} \cdots(1)
z=\pm i b ,f(z) का द्विक अनन्तक है।इनमें से केवल z=ib ऊपरी अर्ध तल में स्थित है।
z=ib पर अवशेष
\phi^{\prime}(i b)=\left[D \frac{e^{i a z}}{(z+i b)^2}\right]_{z=i b}\\ =\left[\frac{i a e^{i a z}(z+i b)^2-2 e^{ia z}(z+i b)}{(z-i b)^4}\right]_{z=ib} \\ =\frac{e^{-a b}[i a(2 i b)-2]}{(2 i b)^3} \\ =\frac{e^{-a b}}{4 b^3 i}(a b+1)
समीकरण (1) सेः
\int_{-\infty}^{\infty} \frac{e^{i a x}}{\left(x^2+b^2\right)^2} d x=2 \pi i \cdot \frac{e^{-a b}}{4 i b^3}(a b+1) \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\cos a x+i \sin a x}{\left(x^2+b^2\right)^2} d x=\frac{\pi e^{-a b}}{2 b^3}(a b+1)
दोनों पक्षों के वास्तविक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{\cos a x}{\left(x^2+b^2\right)^2} d x=\frac{\pi(a b+1)}{2 b^3 e^{a b}} \\ \Rightarrow \int_0^{\infty} \frac{\cos a x}{\left(x^2+b^2\right)^2} d x=\frac{\pi(1+a b)}{4 b^3 e^{a b}}
Illustration:5.सिद्ध करो कि (prove that)
\int_0^{\infty} \frac{\cos x}{\left(x^2+1\right)^2} d x=\frac{\pi}{2 e}
Solution: \int_c \frac{e^{i z}}{\left(z^2+1\right)^2} d z=\int_c f(z) d z पर विचार करें जहाँ C परिरेखा है।
कोशी अवशेष प्रमेय सेः
\int_c f(z) d z=\int_{-R}^R \frac{e^{i x}}{\left(x^2+1\right)^2} d x+\int_{\Gamma} \frac{e^{i z}}{\left(z^2+1\right)^2} d z=2 \pi i \Sigma R^{+}
जोरदाँ उपप्रमेय सेः
\underset{R \rightarrow \infty}{\lim} \int_{\Gamma} \frac{e^{i z}}{\left(z^2+1\right)^2}=0 \\ \therefore \underset{R \rightarrow \infty}{\lim} \int_{-R}^R \frac{e^{i x}}{\left(x^2+1\right)^2} d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{i x}}{\left(x^2+1\right)^2} d x=2 \pi i \Sigma R^{+}
z=\pm i ,f(z) का द्विक अनन्तक हैं।इनमें से केवल z=i ऊपरी अर्धतल में स्थित है।
z=i पर अवशेष
\phi^{\prime}(i) =\left[D\frac{ e^{i z}}{(z+i)^2}\right]_{z=i} \\ =\left[\frac{i e^{i z}(z+i)^2-2 e^{i z}(z+i)}{(z+i)^4}\right]_{z=i} \\ =e^{-1}\left[\frac{i(2 i)-2}{(2 i)^3}\right]=\frac{e^{-1}}{4 i}(2)
समीकरण (1) से:
\int_{-\infty}^{\infty} \frac{e^i x}{\left(x^2+1\right)^2} d x=2 \pi i \cdot \frac{e^{-1}}{4 i}(2) \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\cos x+i \sin x}{\left(x^2+1\right)^2} d x=\pi e^{-1}
दोनों पक्षों के वास्तविक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{\cos x}{\left(x^2+1\right)^2} d x=\frac{\pi}{e} \\ \Rightarrow \int_0^{\infty} \frac{\cos x}{\left(x^2+1\right)^2} d x=\frac{\pi}{2 e}
Illustration:6.मान ज्ञात करो (Evaluate)
\int_0^{\infty} \frac{\cos ^2 x}{\left(1+x^2\right)^2} d x
Solution:माना I=\int_0^{\infty} \frac{\cos ^2 x}{\left(1+x^2\right)^2} d x=\frac{1}{2} \int_0^{\infty} \frac{1+\cos 2x}{\left(1+x^2\right)^2} dx \\ \int_c f(z) d z=\int_c \frac{1+e^{2 i z}}{\left(1+z^2\right)^2} d z , जहाँ C परिरेखा है।
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=\int_{-R}^R f(x) d x+\int_{\Gamma} f(z) d z=2 \pi i \Sigma R^{+}
जोरदाँ उपप्रमेय सेः
\underset{R \rightarrow 0}{\lim} \int_{\Gamma} f(z) d z=0 \\ \therefore \underset{R \rightarrow \infty}{\lim} \int_{-R}^R f(x) d x=2 \pi i \Sigma R^{+} \\ \Rightarrow \int_{-\infty}^{\infty} f(x) d x=2 \pi i \Sigma R^{+} \cdots(1)
z=\pm i ,f(z) का द्विक अनन्तक है जिनमें z=i,C के अन्दर स्थित है।
z=i पर अवशेषः
\phi^{\prime}(i)=\left[\frac{d}{d z} \frac{1+e^{i 2 z}}{(i+2)^2}\right]_{z=i} \\ =\left[\frac{2 i e^{i2 z}(i+z)^2-\left(1+e^{i 2z}\right) 2(i+z)}{(i+z)^4}\right]_{z=i} \\ =\frac{2 i e^{-2} \cdot 2 i-2\left(1+e^{-2} \right)}{2 i} \\ =\frac{-4 e^{-2}-2\left(1+e^{-2}\right)}{-8 i} \\ =\frac{1+3 e^{-2}}{4 i}
समीकरण (1) सेः
\int_{-\infty}^{\infty} \frac{1+e^{i 2 x}}{\left(1+x^2\right)^2} d x=2 \pi i\left(\frac{1+3 e^{-2}}{4 i}\right) \\ \Rightarrow \int_{-\infty}^{\infty} \frac{1+e^{i 2 x}}{\left(1+x^2\right)^2}=\frac{\pi}{2}\left(1+3 e^{-2} \right)
दोनों पक्षों के वास्तविक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{1+\cos 2 x}{\left(1+x^2\right)^2} d x=\frac{\pi}{2}\left(1+3 e^{-2}\right) \\ \Rightarrow \int_0^{\infty} \frac{1+\cos 2 x}{\left(1+x^2\right)^2} d x=\frac{\pi}{4}\left(1+3 e^{-2}\right)
Illustration:7.सिद्ध करो कि (Prove that)
\int_0^{\infty} \frac{\cos m x}{x^4+a^4} d x=\frac{\pi}{2 a^3} e^{-\frac{m a}{\sqrt{2}}} \sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{2}\right)
निगमन कीजिए (Deduce that)
\int_0^{\infty} \frac{x \sin m x}{x^4+a^4} d x=\frac{\pi}{2 a^3} e^{-\frac{m a}{\sqrt{2}}} \sin \frac{ma}{\sqrt{2}}
Solution: \int_C \frac{e^{i m z}}{z^4+a^4} d z=\int_C f(z) d z पर विचार करो,जहाँ C परिरेखा है।
कोशी अवशेष प्रमेय सेः
\int_C f(z) d z=\int_{-R}^R f(x) d x+\int_{\Gamma} f(z) d z=2 \pi i \Sigma R^{+}
जोरदाँ उपप्रमेय सेः
\underset{R \rightarrow \infty}{\lim} \int_{\Gamma} f(z) d z=0
जब R \rightarrow \infty तब \int_{-\infty}^{\infty} f(x) d x=2 \pi i \Sigma R^{+} \cdots(1)
f(z) के अनन्तक दिए जाते हैं z^4+a^4=0 \Rightarrow z=a e^{i(2 n+1) \frac{\pi}{4}}, n=0,1,2,3
इस प्रकार z=a e^{i \frac{\pi}{4}}, a e^{3 i \frac{\pi}{4}}, a e^{5 i \frac{\pi}{4}}, a e^{\frac{7 i \pi}{4}}, f(z) के साधारण अनन्तक हैं।इनमें से केवल दो C के अन्दर स्थित हैं।
इनमें से एक को \alpha द्वारा प्रदर्शित करें तो
z=\alpha पर अवशेष=\left[\frac{e^{i m z}}{D\left(z^4+a^4\right)} \right]_{z=\alpha}=\frac{e^{i m \alpha}}{4 \alpha^3}
C के अन्दर अनन्तको पर अवशेषों का योग :
=\frac{1}{4}\left[\frac{e^{i m a e^i{ \frac{\pi}{4}}}}{a^3 e^{\frac{i 3 \pi}{4}}}+\frac{e^{i m a e^{\frac{3 i \pi}{4}}}}{a^3 e^{\frac{9i \pi}{4}}}\right] \\ =\frac{1}{4 a^3}\left[\frac{e^{i m a \frac{(1+i)}{\sqrt{2}}}}{-e^{-\frac{i \pi}{4}}}+\frac{e^{i m a \frac{(-1+i)}{\sqrt{2}}}}{e^{\frac{i \pi}{4}}}\right] \\ =\frac{e^{-\frac{m a}{\sqrt{2}}}}{4 a^3}\left[\frac{e^{\frac{i m a}{\sqrt{2}}}}{-e^{-\frac{i \pi}{4}}}+\frac{e^{\frac{i m a}{\sqrt{2}}}}{e^{\frac{i \pi}{4}}}\right] \\ =\frac{-e^{-\frac{m a}{\sqrt{2}}}}{4 a^3}\left[\exp \left(\frac{m a}{\sqrt{2}} +\frac{\pi}{4}\right) i-\exp \left(-\frac{m a}{\sqrt{2}}-\frac{\pi}{4}\right)i\right] \\ =\frac{-e^{-m a} \sqrt{2}}{4 a^3} \cdot 2 i \sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right)
समीकरण (1) सेः
\int_{-\infty}^{\infty} \frac{e^{i m x}}{x^4+a^4} d x=\frac{\pi}{a^3} e^{-\frac{m a}{\sqrt{2}}} \sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right)
दोनों पक्षों के वास्तविक भागों की तुलना करने परः
\int_{-\infty}^{\infty} \frac{\cos m x}{x^4+a^4} d x=\frac{\pi}{a^3} e^{-\frac{m a}{\sqrt{2}}} \sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right) \\ \int_0^{\infty} \frac{\cos m x}{x^4+a^4} d x=\frac{\pi}{2 a^3} e^{-\frac{m a}{\sqrt{2}}} \sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right)
दोनों पक्षों का m के सापेक्ष अवकलन करने पर :
\int_0^{\infty} \frac{-x \sin m x}{x^4+a^4} d x=\frac{\pi}{2 a^3}\left[e^{-\frac{m a}{\sqrt{2}}}\left(-\frac{a}{\sqrt{2}}\right) \sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right)+e^{-\frac{m a}{\sqrt{2}}} \cos \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right) \cdot \frac{a}{\sqrt{2}}\right] \\ =\frac{a \pi e^{-\frac{m a}{\sqrt{2}}}}{2 \sqrt{2} a^3}\left[-\sin \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right) \cos \left(\frac{m a}{\sqrt{2}}+\frac{\pi}{4}\right)\right] \\ =-\frac{\pi}{2 a^2} e^{-\frac{m a}{\sqrt{2}}} \sin \left(\frac{m a}{\sqrt{2}}\right) \\ \Rightarrow \int_0^{\infty} \frac{x \sin m x}{x^4+a^4} d x=\frac{\pi}{2 a^2} e^{-\frac{m a}{\sqrt{2}}} \sin \left(\frac{m a}{\sqrt{2}}\right)
उपर्युक्त उदाहरणों के द्वारा परिरेखा समाकलन का मूल्यांकन (Evaluation of Contour Integration),परिरेखा समाकलन (Contour Integration) को समझ सकते हैं।
Also Read This Article:- Illustrations of Contour Integration
3.परिरेखा समाकलन का मूल्यांकन (Frequently Asked Questions Related to Evaluation of Contour Integration),परिरेखा समाकलन (Contour Integration) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.परिरेखा का दन्तुरण को स्पष्ट करो। (Explain the Indenting of the Contour):
उत्तर:यदि फलन के अनन्तक वास्तविक अक्ष पर स्थित हैं तो परिरेखा पर फलन का समाकलन नहीं किया जा सकता है।लेकिन इन अनन्तकों को टालने के लिए,इन अनन्तकों को केन्द्र मानते हुए छोटी त्रिज्या वाले अर्धवृत्तों का निर्माण करते हैं।इस प्रक्रिया को अर्धवृत्तीय परिरेखा का दन्तुरण (indenting) कहते हैं।
प्रश्न:2.बहुमानी फलनों का समाकलन किससे किया जा सकता है? (What Are the Integral of Many Vaued Functions?):
उत्तर:बहुमानी फलनों जैसे z^{\alpha} ( \alpha पूर्णांक नहीं), \log z आदि का समाकलन भी अर्धवृत्तीय परिरेखा के दन्तुरण विधि द्वारा किया जा सकता है।इसमें शाखा बिन्दु को, उसी बिन्दु पर केन्द्रित उपरि अर्धतल में स्थित,छोटी त्रिज्या वाले वृत्त द्वारा टाला जाता है।
प्रश्न:3.परिमेय फलनों के समाकलन करने के लिए किस शर्त का पालन करना आवश्यक है? (Which Condition Must be Followed to Perform the Integration of Rational Functions?):
उत्तर:f(x) परिमेय फलन है तथा इसके अभिसारी होने के लिए यह आवश्यक है (i)f(x) में हर की कोटि अंश की कोटि से अधिक हो, (ii)f(x) के हर का कोई भी शून्य x-अक्ष पर नहीं हो।अतः इन प्रतिबन्धों के अन्तर्गत ही \int_{-\infty}^{\infty} f(x) \sin m x dx तथा \int_{-\infty}^{\infty} f(x) \cos m x d x, m \geq 0 प्रकार के समाकलों का मूल्यांकन किया जा सकता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा परिरेखा समाकलन का मूल्यांकन (Evaluation of Contour Integration),परिरेखा समाकलन (Contour Integration) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here | |
| 7. | click here |
Evaluation of Contour Integration
परिरेखा समाकलन का मूल्यांकन
(Evaluation of Contour Integration)
Evaluation of Contour Integration
परिरेखा समाकलन का मूल्यांकन (Evaluation of Contour Integration) के इस आर्टिकल
में परिरेखा समाकलन पर आधारित विशिष्ट सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.