Euclid Geometry Class 9
1.यूक्लिड की ज्यामिति कक्षा 9 (Euclid Geometry Class 9),यूक्लिड की ज्यामिति का परिचय (Euclid’s Geometry Introduction):
- यूक्लिड की ज्यामिति कक्षा 9 (Euclid Geometry Class 9) में प्रारम्भ से लेकर अब तक उत्पत्ति के बारे में अध्ययन करेंगे।
शब्द ‘ज्यामिति’ (geometry) यूनानी भाषा के शब्दों ‘जियो’ (geo) और ‘मीट्रीन’ (metrein) से मिलकर बना है।जियो का अर्थ ‘पृथ्वी’ या ‘भूमि’ और मीट्रीन का अर्थ है ‘मापना’। इससे ऐसा प्रतीत होता है कि ज्यामिति का उद्गम भूमि मापने की आवश्यकता के कारण हुआ है।गणित की इस शाखा का अध्ययन विभिन्न रूपों में प्रत्येक प्राचीन सभ्यताओं द्वारा किया गया चाहे वह मिस्र हो, बेबीलोन हो, चीन हो, भारत हो, यूनान हो या इनका (incas) इत्यादि।इन सभ्यताओं के लोगों को अनेक व्यावहारिक समस्याओं का सामना करना पड़ा जिनमें ज्यामिति के विकास की विभिन्न प्रकार से आवश्यकता पड़ी। - आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Mean Median and Mode Class 9
2.मिस्र में ज्यामिति का विकास (Geometry Developed in Egypt):
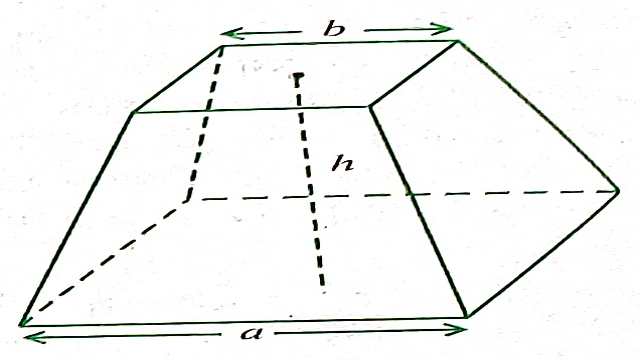
- उदाहरण के तौर पर जब भी नील नदी में बाढ़ आती थी तो विभिन्न भूमि स्वामियों के संलग्न खेतों के बीच की परिसीमाओं (boundaries) को अपने साथ बहा ले जाती थी।इन बाढ़ों के बाद, इन परिसीमाओं को पुनः बनाया जाता था।इस कार्य के लिए,मिस्रवासियों ने सरल क्षेत्रफल परिकलित करने के साथ ही सरल रचनाएँ करने के लिए,अनेक ज्यामितीय तकनीकें और नियम विकसित किए।उन्होंने ज्यामिति के ज्ञान का उपयोग अन्न भण्डारों के आयतन निकालने तथा नहरों और पिरामिड़ों (Pyramids) के निर्माण में किया।वे एक कटे हुए पिरामिड (truncated pyramids) (देखिए आकृति) का आयतन ज्ञात करने का सही सूत्र भी जानते थे।आप जानते हैं कि पिरामिड एक ऐसी ठोस आकृति होती है जिसका आधार एक त्रिभुज या वर्ग या कोई अन्य बहुभुज होता है और जिसके पार्श्व फलक (side faces या lateral faces) ऊपर एक ही बिन्दु पर मिलने वाले त्रिभुज होते हैं।
3.भारत में ज्यामिति का विकास (Geometry Evolved in India):
- भारतीय उपमहाद्वीप में हड़प्पा और मोहनजोदड़ो इत्यादि की खुदाइयों से यह पता लगता है कि सिन्धु घाटी की सभ्यता (लगभग 3000 ई.पू.) ने ज्यामिति का प्रचुर मात्रा में उपयोग किया।वह एक उच्च कोटि का संगठित समाज था।शहर अत्याधुनिक रूप से विकसित थे और बड़े योजनाबद्ध ढंग से निर्मित किए गए थे। उदाहरणार्थ सड़कें परस्पर समान्तर होती थी और भूमिगत नालियों की व्यवस्था थी।घरों में विभिन्न प्रकार के अनेक कमरे हुआ करते थे।ये बातें दर्शाती है कि नगरवासी क्षेत्रमिति (mesuration) और अंकगणित में पूर्ण रूप से निपुण थे।निर्माण कार्य में प्रयोग की जाने वाली ईंटें भट्टों पर पकाई (बनाई) जाती थी और इन ईंटों के लिए अनुपात लम्बाईःचौड़ाईःमोटाई, 4:2:1 होता था।
- प्राचीन भारत में,सुल्बासूत्र (800 ई.पू.-500 ई. पू.) ज्यामितीय रचनाओं के लिए महत्त्वपूर्ण ग्रन्थ थे।वैदिक काल की ज्यामिति का उद्गम वैदिक पूजा के लिए आवश्यक भिन्न-भिन्न प्रकार की वेदियों और अग्नि-कुण्डों के निर्माण कार्य से हुआ।पवित्र अग्नियों को अधिक प्रभावशाली साधक होने के लिए उनके स्थान,उनके आकारों और क्षेत्रफलों के बारे में स्पष्ट रूप से निर्धारित अनुदेशों के अनुसार होते थे।घरेलू धार्मिक क्रियाओं के लिए वर्गाकार और वृत्ताकार वेदियों का प्रयोग किया जाता था जबकि सार्वजनिक पूजा स्थलों के लिए आयतों,त्रिभुजों और समलम्बों के संयोजनों (मिले जुले) से बने आकारों का प्रयोग आवश्यक होता था। (अथर्ववेद में दिए) ‘श्रीयंत्र’ में एक दूसरे के जुड़े नौ समद्विबाहु त्रिभुज अंतर्निहित हैं।ये त्रिभुज इस प्रकार व्यवस्थित किए गए हैं कि इनसे 43 छोटे (या गौण) त्रिभुजों का निर्माण होता है।यद्यपि वेदियों की रचना करने में परिशुद्घ ज्यामितीय विधियों का उपयोग किया गया था, फिर भी इनसे सम्बन्धित सिद्धान्तों की कोई चर्चा नहीं की गई।
- उपर्युक्त उदाहरण यह दर्शाते हैं कि ज्यामिति का विकास और अनुप्रयोग विश्व के सभी स्थानों पर होता रहा।परन्तु यह बड़े अव्यवस्थित प्रकार से हो रहा था।प्राचीन विश्व में,ज्यामिति के विकास की इन गतिविधियों की एक रोचक बात यह है कि इन ज्ञान एक पीढ़ी से दूसरी पीढ़ी को या तो मौखिक रूप से या ताड़ के वृक्ष की पत्तियों पर लिखे संदेशों या कुछ अन्य विधियों द्वारा दिया जाता रहा।साथ ही, हम यह भी पाते हैं कि कुछ सभ्यताओं,जैसे कि बेबीलोनिया में,ज्यामिति एक अत्याधिक व्यावहारिक दृष्टिकोण वाले विषय तक सीमित रही तथा ऐसा ही भारत और रोम में रहा।मिस्रवासियों द्वारा विकसित की गई ज्यामिति में मुख्यतः परिणामों के कथन ही निहित थे।इनमें प्रक्रियाओं (अथवा विधियों) के कोई व्यापक नियम नहीं दिए गए।वस्तुतः बेबीलोन और मिस्रवासियों दोनों ही ने ज्यामिति का उपयोग अधिकांशत व्यावहारिक कार्यो के लिए ही किया तथा उसको एक क्रमबद्ध विज्ञान के रूप में विकसित करने के लिए बहुत कम काम किया।परन्तु यूनान जैसी सभ्यताओं में इस तर्क पर बल दिया जाता था कि कुछ रचनाएँ किस प्रकार हो जाती हैं।यूनानियों की अभिरुचि उन कथनों,जिनको उन्होंने स्थापित किया था,की सत्यता निगमनिक तर्कण (deductive reasoning) का उपयोग करके जांचने में थी।
4.यूनानी गणितज्ञ थेल्स का परिचय दें (Introduce the Greek Mathematician Thales):
- एक यूनानी गणितज्ञ थेल्स (Thales) को श्रेय जाता है कि उन्होंने सबसे पहली ज्ञात उपपत्ति (Proof) प्रदान की।यह उपपत्ति इस कथन की थी कि वृत्त का व्यास वृत्त को समद्विभाजित (अर्थात् दो बराबर भागों में विभाजित) करता है।थेल्स का एक सबसे प्रसिद्ध शिष्य पाइथागोरस (572 ई.पू.) था जिसका नाम आपने अवश्य सुना होगा।पाइथागोरस और उसके साथियों ने अनेक ज्यामितीय गुणों की खोज की और ज्यामिति के सिद्धान्तों का अत्याधिक विकास किया।यह प्रक्रिया 300 ई.पू. तक जारी रही।
5.यूक्लिड का परिचय दें (Introduce Euclid):
- इसी समय मिस्र में अलेक्जेंड्रिया के एक गणित शिक्षक यूक्लिड (Euclid) ने उस समय तक ज्ञात गणित के सभी ज्ञान को एकत्रित किया और एलीमेंट्स (Elements) नामक अपने प्रसिद्ध ग्रन्थ के रूप में उसे व्यवस्थित किया।उन्होंने एलीमेंट्स को 13 अध्यायों में विभाजित किया जिनमें से प्रत्येक को ‘पुस्तिका’ माना जाता है।इन पुस्तिकाओं ने समस्त विश्व की ज्यामिति सम्बन्धी समझ को आने वाली पीढ़ियों तक प्रभावित किया।
6.यूक्लिड परिभाषाएँ,अभिगृहीत और अभिधारणाएँ (Euclid’s Definitions Axioms and Postulates):
- यूक्लिड के समय के यूनानी गणितज्ञों ने ज्यामिति को उस विश्व का एक सिद्धांतीय प्रतिमान (model) सोचा जिसमें वे रहते थे।बिन्दु (point),रेखा (line),तल (Plane) [या पृष्ठ (Surface)] इत्यादि की अवधारणाएँ उन वस्तुओं से स्थापित की गई जो उनके आसपास थी।आकाश (Space) और उनके आसपास के ठोसों के अध्ययनों के आधार पर,एक ठोस वस्तु की सिद्धांतीय ज्यामितीय अवधारणा विकसित की गई।एक ठोस (solid) का आकार होता है,माप और स्थिति होती है तथा उसे एक स्थान से दूसरे स्थान तक ले जाया जा सकता है।इसकी परिसीमाएँ पृष्ठ (Surface) कहलाती हैं। ये आकाश के एक भाग को दूसरे भाग से पृथक करती हैं और इनकी कोई मोटाई नहीं होती है।पृष्ठों की परिसीमाएँ वक्र (Curves) या सीधी रेखाएँ (lines) होती है।इन रेखाओं के सिरे बिन्दु (points) होते हैं।
- यह कहा जाता है कि एक ठोस की तीन विमाएँ होती हैं,एक पृष्ठ की दो विमाएँ, एक रेखा की एक विमा होती है और एक बिन्दु की कोई विमा नहीं होती।यूक्लिड ने इन कथनों को संक्षिप्त रूप से परिभाषाओं के रूप में प्रस्तुत किया।इनमें से कुछ परिभाषाएँ नीचे दी जा रही हैं:
- (1.)एक बिन्दु (point) वह है जिसका कोई भाग नहीं होता।
- (2.)एक रेखा (line) चौड़ाई रहित लम्बाई होती है।
- (3.)एक रेखा के सिरे बिन्दु होते हैं।
- (4.)एक सीधी रेखा ऐसी रेखा है जो स्वयं पर बिन्दुओं के साथ सपाट रूप से स्थित होती है।
- (5.)एक पृष्ठ (Surface) वह है जिसकी केवल लम्बाई और चौड़ाई होती है।
- (6.)पृष्ठ के किनारे (edges) रेखाएँ होती हैं।
- (7.)एक समतल पृष्ठ (Plane surface) ऐसा पृष्ठ है जो स्वयं पर सीधी रेखाओं के साथ सपाट रूप से स्थित होता है।
- अपनी इन परिभाषाओं से प्रारम्भ करते हुए,यूक्लिड ने कुछ गुणों को बिना सिद्ध किए सत्य कथन मानने की कल्पना की।ये कल्पनाएँ वास्तव में ‘स्पष्टतः सर्वव्यापी सत्य’ थे।उन्होंने इनको दो वर्गों में विभाजित किया।ये वर्ग थेःअभिगृहीत (Axioms) और अभिधारणाएँ (postulates)।उन्होंने अभिधारणा शब्द का प्रयोग उन कल्पनाओं के लिए किया जो विशिष्ट रूप से ज्यामिति से सम्बन्धित थी।दूसरी ओर, सामान्य अवधारणाएँ [जिन्हें प्रायः अभिगृहीत (axioms) कहा गया] वे कल्पनाएँ थी जिन्हें निरन्तर गणित में प्रयोग किया गया और जिनका केवल ज्यामिति से विशेष सम्बन्ध नहीं था। यूक्लिड के कुछ अभिगृहीतों को बिना उनके क्रम के नीचे दिया जा रहा हैः
- (1.)वे वस्तुएँ जो एक ही वस्तु के बराबर हों एक दूसरे के बराबर होती हैं।
- (2.)यदि बराबरों को बराबरों में जोड़ा जाए,तो पूर्ण भी बराबर होते हैं।
- (3.)यदि बराबरों को बराबरों में से घटाया जाए, तो शेषफल भी बराबर होते हैं।
- (4.)वे वस्तुएँ जो परस्पर संपाती हों, एक-दूसरे के बराबर होती हैं।
(5.)पूर्ण अपने भाग से बड़ा होता है। - (6.)एक ही वस्तुओं के दुगुने परस्पर बराबर होते हैं।
- (7.)एक ही वस्तुओं के आधे परस्पर बराबर होते हैं।
अभिधारणा:1. - एक बिन्दु से एक अन्य बिन्दु तक एक सीधी रेखा खींची जा सकती है।
यह अभिधारणा हमें बताती है कि दो भिन्न (distict) बिन्दुओं से होकर कम से कम एक रेखा अवश्य खींची जा सकती है परन्तु इससे यह नहीं ज्ञात होता कि ऐसी एक से अधिक सीधी रेखाएँ नहीं हो सकती।परन्तु अपने समस्त कार्यों में यूक्लिड ने,बिना कुछ बताए,यह बार-बार कल्पना की है कि दो भिन्न बिन्दुओं से एक अद्वितीय (Unique) रेखा ही खींची जा सकती है।
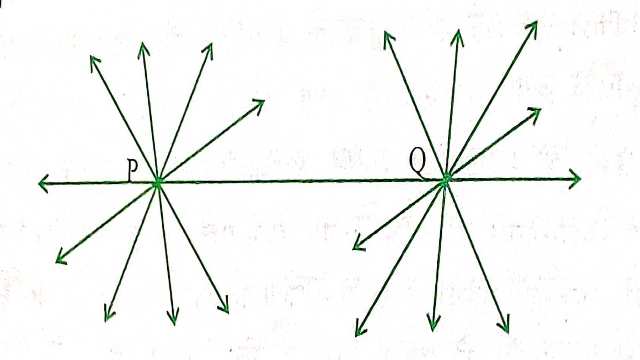
अभिगृहीतःदिए हुए दो भिन्न बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है। - बिन्दु P से होकर कितनी रेखाएँ खींची जा सकती है जो बिन्दु Q से होकर भी जाती हो (देखिए आकृति)? केवल एक।यह रेखा PQ है।बिन्दु Q से होकर जाने वाली ऐसी कितनी रेखाएँ हैं जो बिन्दु P से होकर जाती है? केवल एक अर्थात् रेखा PQ।इस प्रकार उपर्युक्त कथन एक स्वयं सिद्ध (self evident) सत्य है और इसीलिए हम इसे अभिगृहीत के रूप में मान लेते हैं।
- अभिधारणा:2.
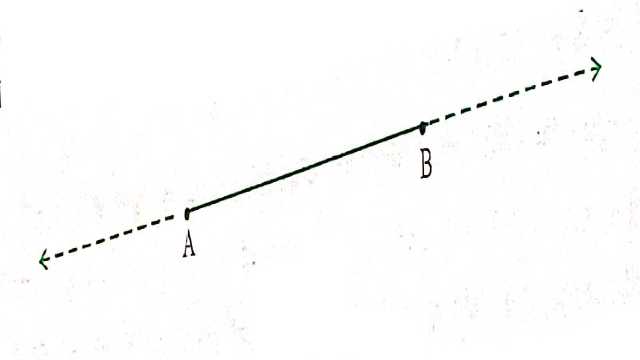
- एक सांत रेखा (terminated line) को अनिश्चित रूप से बढ़ाया जा सकता है।
जिसको हम आजकल रेखाखण्ड (line segment) कहते हैं उसे यूक्लिड ने सांत रेखा कहा था।अतः वर्तमान की भाषा में,दूसरी अभिधारणा कहती हैं कि एक रेखाखण्ड को दोनों ओर विस्तृत करके एक रेखा बनाई जा सकती है (देखिए आकृति)
- अभिधारणा:3.
- किसी को केन्द्र मानकर और किसी त्रिज्या से एक वृत्त खींचा जा सकता है।
अभिधारणाः4. - सभी समकोण एक दूसरे के बराबर होते हैं।
अभिधारणाः5. - यदि एक सीधी रेखा दो सीधी रेखाओं पर गिरकर अपने एक ही ओर दो अंतः कोण (interior angle) इस प्रकार बनाए कि इन दोनों कोणों का योग मिल कर दो समकोणों से कम हो, तो वे दोनों सीधी रेखाएँ अनिश्चित रूप से बढ़ाए जाने पर उसी ओर मिलती हैं जिस ओर यह योग दो समकोणों से कम होता है।
- उदाहरणार्थ आकृति में रेखा PQ रेखाओं AB और CD पर इस प्रकार गिरती है कि अन्तःकोणों 1 और 2 का योग जो PQ के बाईं ओर स्थित हैं, 180° से कम है।अतः रेखाएँ AB और CD अंततः PQ के बाई ओर प्रतिच्छेद करेंगी।
7.यूक्लिड की ज्यामिति कक्षा 9 के साधित उदाहरण (Euclid Geometry Class 9 Solved Examples):
- Example:1.निम्नलिखित कथनों में से कौन-से कथन सत्य हैं और कौन-से कथन असत्य हैं? अपने उत्तरों के लिए कारण दीजिए।
Example:1(i).एक बिन्दु से होकर केवल एक ही रेखा खींची जा सकती है।
Solution:असत्य।क्योंकि एक बिन्दु से अनन्त रेखाएँ खींची जा सकती है।यह स्वयं सिद्ध है।
Example:1(ii).दो भिन्न बिन्दुओं से होकर जानेवाली असंख्य रेखाएँ हैं।
Solution:असत्य।यह कथन यूक्लिड के अभिगृहीत 1 का अन्तर्विरोध करता है जिसके अनुसार दिए हुए दो भिन्न बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
Example:1(iii).एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
Solution:सत्य।क्योंकि यूक्लिड की अभिधारणा 2 के अनुसार एक सांत रेखा (terminated line) को अनिश्चित रूप से बढ़ाया जा सकता है।
Example:1(iv).यदि वृत्त बराबर हैं तो उनकी त्रिज्याएँ बराबर होती हैं।
Solution:सत्य।यूक्लिड के अभिगृहीत 4 के अनुसार वे वस्तुएँ जो परस्पर संपाती हों एक दूसरे के बराबर होती हैं। यदि एक वृत्त से परिबद्ध प्रदेश को दूसरे प्रदेश पर अध्यारोपित करें तो वे संपाती होंगे।अतः इनके केन्द्र और परिसीमाएँ संपाती होती हैं।फलतः इनकी त्रिज्या संपाती होती है।
Example:1(v).आकृति में यदि AB=PQ और PQ=XY हो तो AB=XY होगा।
- Solution:सत्य।कारण कि यूक्लिड की अभिगृहीत 1 का कथन है कि वे वस्तुएँ जो एक ही वस्तु के बराबर हों,एक दूसरे के बराबर होती हैं।
Example:2.निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए।क्या इनके लिए कुछ ऐसे पद हैं जिन्हें परिभाषित करने की आवश्यकता है? वे क्या है और इन्हें कैसे परिभाषित कर पाएंगे?
Example:2(i).समान्तर रेखाएँ
Solution:समान्तर रेखाएँ (parallel lines) वे सीधी रेखाएँ हैं जो कि एक तल पर होती हैं और दोनों दिशाओं में असीमित रूप में बढ़ाने पर एक-दूसरे को किसी भी दिशा में नहीं मिलती।
Example:2(ii).लम्ब रेखाएँ
Solution:एक एक सीधी रेखा,किसी अन्य सीधी रेखा पर इस प्रकार खड़ी हो कि आसन्न कोण एक दूसरे के बराबर बने तो प्रत्येक समान कोण समकोण होता है और सीधी रेखा जो दूसरी पर खड़ी है,उस पर लम्ब रेखा कहलाती है जिस पर यह खड़ी है।अन्य पद जिन्हें परिभाषित करने की आवश्यकता है,ये हैंः
(i)कोण (Angle):एक समतल कोण (Plane angle) समतल में मिलनी वाली दो रेखाओं का एक-दूसरे के साथ झुकाव है जो एक दूसरे को मिलती हैं।
(ii)आसन्न कोण (adjacent angels):दो कोण जिनका एक ही शीर्ष होता है,एक भुजा उभयनिष्ठ होती है और दूसरी अन्य दो भुजाएँ उभयनिष्ठ भुजा के विपरीत दिशाओं में होती है,आसन्न कोण होते हैं।
(iii) समकोण (Right angle):यह कोण जो कि सम्पूर्ण कोण का एक चौथाई होता है,समकोण कहलाता है।
Example:2(iii).रेखाखण्ड
Solution:एक रेखाखण्ड जो दोनों दिशाओं में असीमित रूप से बढ़ाने पर रेखा देती है।
Example:2(iv).वृत्त की त्रिज्या
Solution:एक रेखाखण्ड जो वृत्त के किसी बिन्दु को केन्द्र से मिलाता है,वृत्त की त्रिज्या कहलाता है। अन्य पद जिन्हें परिभाषित करने की आवश्यकता है।
(i)वृत्त (Circle):वृत्त किसी तल में बनी वह बन्द आकृति है जिसके तल में सभी बिन्दु एक निश्चित बिन्दु से समान दूरी पर होते हैं।
(ii)वृत्त का केन्द्र (Centre of Circle):वह स्थिर बिन्दु जिससे वृत्त पर स्थित सभी बिन्दु एक समान दूरी पर स्थित हो वृत्त का केन्द्र कहलाता है।
Example:2(v).वर्ग
Solution:वर्ग वह चतुर्भुजाकार आकृति है जो समभुज और समकोणिक दोनों ही हों।अन्य पद जिन्हें परिभाषित करने की आवश्यकता हैः
(i)समभुज (Equilateral):वह आकृति जिसकी सभी भुजाएँ बराबर हों समभुज या समबाहु कहलाती है।
(ii)समकोण (Right angle):एक कोण जो संपूर्ण कोण का एक चौथाई होता है,समकोण कहलाता है।
Example:3.नीचे दी गई अभिधारणाओं पर विचार कीजिएः
(i) दो भिन्न बिन्दु A और B दिए रहने पर,एक तीसरा बिन्दु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
(ii) यहाँ कम से कम ऐसे तीन बिन्दु विद्यमान है कि वे एक रेखा पर स्थित नहीं है।
क्या इन अभिधारणाओं में कोई अपरिभाषित शब्द है? क्या ये अभिधारणाएँ अविरोधी है? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती हैं? स्पष्ट कीजिए।
Solution:हाँ, ऐसे अनेक अपरिभाषित शब्द हैं जिनकी जानकारी छात्र को होनी चाहिए।ये दो अभिधारणाएँ (i) और (ii) संगत हैं क्योंकि इनमें दो अलग-अलग स्थितियों का अध्ययन किया जाता है।अभिधारणा (i) का कथन है कि यदि दो बिन्दु A और B दिए हुए हों तो उनके बीच में स्थित एक बिन्दु C होता है।
- अभिधारणा (ii) का कथन है कि दो दिए हुए बिन्दुओं A और B के लिए हम एक बिन्दु C ले सकते हैं।जो A और B से होकर जाने वाली रेखा पर स्थित नहीं होता।
- अतः हम देखते हैं कि ये अभिगृहीत यूक्लिड के अभिगृहीतों का अनुसरण नहीं करते हैं।फिर भी ये अभिगृहीत (1) का अनुसरण करते हैं जिसके अनुसार दिए गए दो बिन्दुओं के लिए भिन्न एक अद्वितीय रेखा होती है जो उनमें से होकर जाती है।
- Example:4.यदि दो बिन्दुओं A और B के बीच एक बिन्दु C ऐसा स्थित है कि AC=BC है,तो सिद्ध कीजिए कि AC=\left( \frac{1}{2} \right) AB है।एक आकृति खींचकर स्पष्ट कीजिए।
- Solution:दिया है कि C,A और B के बीच स्थित है।
और AC=BC
इसलिए AC+AC=BC+AC
यूक्लिड की परिभाषा के अनुसार बराबरों को बराबरों में जोड़ा गया है।
अर्थात् 2AC=AB [BC+AC,AB के संपाती है]
अतः AC=\left( \frac{1}{2} \right) AB
Example:5.प्रश्न 4 में, C रेखाखण्ड AB का एक मध्य बिन्दु कहलाता है।सिद्ध कीजिए कि एक रेखाखण्ड का एक और केवल एक ही मध्य-बिन्दु होता है।
Solution:मान लीजिए कि AB के दो मध्य-बिन्दु C और D हैं।
- इसलिए यूक्लिड की अभिगृहीत (4) के अनुसार जब रेखा को बिन्दु C पर मोड़ा जाता है तो हम देखते हैं कि भाग BC भाग AC पर अध्यारोपित होता है।
AC=BC …. (1)
इसी प्रकार D,AB का मध्य बिन्दु है।
AD=BD …… (2)
हमें प्राप्त है AB=AB
AC+BC=AD+BD
AC+AC=AD+AD [(1) और (2) का प्रयोग करने पर]
2AC=2AD
AC=AD …. (3)
जब हम AD को AC पर और BD को BC पर अध्यारोपित करते हैं तो हम देखते हैं कि BD पूरी तरह CB को पूरा ढक लेता है।इससे निष्कर्ष निकलता है D और C दो भिन्न बिन्दु नहीं है किन्तु एक ही हैं।अतः हम इस निष्कर्ष पर पहुँचते हैं कि एक रेखाखण्ड का केवल एक ही मध्य-बिन्दु होता है।
Example:6.आकृति में यदि AC=BD है तो सिद्ध कीजिए कि AB=CD है।
- Solution:दिया है किः
AC=BD… (1)
AC=AB+BC [बिन्दु B,A और C के बीच स्थित है] ….(2)
BD=BC+CD [बिन्दु C,B और D के बीच स्थित है] …(3)
(2) और (3) को (1) में प्रतिस्थापित करने परः
AB+BC=BC+CD
दोनों ओर से BC घटाने परः
AB+BC-BC=BC+CD-BC
अतः AB=CD
[बराबरों में से बराबरों को घटाने पर शेषफल भी बराबर होता है]
Example:7.यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना जाता है?
(ध्यान दीजिये कि यह प्रश्न पाँचवीं अभिधारणा से सम्बन्धित नहीं है।)
Solution:यूक्लिड के पाँचवें अभिगृहीत के अनुसार, “यदि दो सरल रेखाओं पर एक सरल रेखा गिरती है और इस प्रकार एक ही ओर बने अन्तःकोणों का योग दो समकोणों से कम है तब दोनों सरल रेखाएँ यदि अनिश्चित रूप से बढ़ाई जाती हैं तो वे उस ओर मिलती हैं जिस ओर कोणों का योग दो समकोण से कम है।चूँकि विश्व के किसी भी भाग में किसी भी वस्तु के लिए यह सत्य होता है।अतः इसे सार्वभौमिक सत्य माना जाता है।
उपर्युक्त उदाहरणों द्वारा यूक्लिड की ज्यामिति कक्षा 9 (Euclid Geometry Class 9),यूक्लिड की ज्यामिति का परिचय (Euclid’s Geometry Introduction) को समझ सकते हैं।
Also Read This Article:-Frequency Distribution Table Class 9
8.यूक्लिड की ज्यामिति कक्षा 9 (Euclid Geometry Class 9),यूक्लिड की ज्यामिति का परिचय (Euclid’s Geometry Introduction) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्न:1.साध्य या प्रमेय किसे कहते हैं? (What is a theorem?):
उत्तरःप्रमेय वे कथन हैं जिन्हें परिभाषाओं,अभिगृहीतों,पहले सिद्ध किए गए कथनों और निगमनिक तर्कण द्वारा सिद्ध किया जाता है।
प्रश्न:2.ज्यामिति में अपरिभाषित पदों से क्या तात्पर्य है? (What is Meant by Undefined Terms in Geometry?):
उत्तरःयद्यपि यूक्लिड ने बिन्दु,रेखा और तल को परिभाषित किया है परन्तु गणितज्ञों ने इन परिभाषाओं को स्वीकार नहीं किया है।इसलिए ज्यामिति में इन्हें अब अपरिभाषित पदों के रूप में लिया जाता है।
प्रश्न:3.अभिगृहीत और अभिधारणाओं से क्या तात्पर्य है? (What is Meant by Axioms and Postulates?):
उत्तरःअभिगृहीत और अभिधारणाएँ ऐसी कल्पनाएँ हैं जो स्पष्टतः सर्वव्यापी सत्य होती है।इन्हें सिद्ध नहीं किया जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा यूक्लिड की ज्यामिति कक्षा 9 (Euclid Geometry Class 9),यूक्लिड की ज्यामिति का परिचय (Euclid’s Geometry Introduction) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Euclid Geometry Class 9
यूक्लिड की ज्यामिति कक्षा 9
(Euclid Geometry Class 9)
Euclid Geometry Class 9
यूक्लिड की ज्यामिति कक्षा 9 (Euclid Geometry Class 9) में प्रारम्भ से लेकर अब तक उत्पत्ति
के बारे में अध्ययन करेंगे।शब्द ‘ज्यामिति’ (geometry) यूनानी भाषा के शब्दों ‘जियो’ (geo) और
‘मीट्रीन’ (metrein) से मिलकर बना है।
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
