Envelope in Mathematics
1.गणित में अन्वालोप (Envelope in Mathematics),एक वक्र का अन्वालोप कैसे ज्ञात करें? (How to Find Envelope of a Curve?):
गणित में अन्वालोप (Envelope in Mathematics) जो किसी वक्र कुल (family of curves) के प्रत्येक सदस्य को स्पर्श करता है तथा स्वयं प्रत्येक बिन्दु पर वक्र कुल के किसी न किसी सदस्य के द्वारा स्पर्श किया जाता हो तो वह उस वक्र कुल का अन्वालोप (Envelope) कहलाता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Envelope When Two Parameters Connected
2.गणित में अन्वालोप के साधित उदाहरण (Envelope in Mathematics Solved Examples):
Example:1.सिद्ध कीजिए कि रेखा कुल x \cos m \alpha+y \sin m \alpha=a(\cos n \alpha)^{\frac{m}{n}} के अन्वालोप का ध्रुवीय समीकरण r^{\frac{n}{m-n}}=a^{\frac{n}{{m-n}}} \cos \left(\frac{n \theta}{m-n}\right) है।
[Prove that the envelope of the family of straight lines x \cos m \alpha+y \sin m \alpha=a(\cos n \alpha)^{\frac{m}{n}} is the curve whose polar equation is r^{\frac{n}{m-n}}=a^{\frac{n}{{m-n}}} \cos \left(\frac{n \theta}{m-n}\right)]
Solution: x \cos m \alpha+y \sin m \alpha=a(\cos n \alpha)^{\frac{m}{n}} \\ x=\cos \theta तथा y=r \sin \theta रखने परः
r \cos \theta \cos m \alpha+r \sin \theta \sin m \alpha=a(\cos n \alpha)^{\frac{m}{n}} \\ \Rightarrow r \cos (\theta-m \alpha)=a(\cos n \alpha)^{\frac{m}{n}} \ldots(1)
दोनों पक्षों का लघुगणक लेने परः
\log r+\log \cos (\theta-m \alpha)=\log a+\frac{m}{n} \log (\cos n \alpha) \ldots(2)\\ \alpha के सापेक्ष आंशिक अवकलन करने परः
0+\frac{\sin (\theta-m \alpha)}{\cos (\theta-m \alpha)}=-\frac{n}{n} \cdot n \frac{\sin n \alpha}{\cos n \alpha} \\ \Rightarrow \tan (\theta-m \alpha)=-\tan n \alpha \\ \Rightarrow \tan (\theta-m \alpha)=\tan (-n \alpha) \\ \Rightarrow \theta-m \alpha=-n \alpha \\ \Rightarrow \theta=m \alpha-n \alpha \\ \Rightarrow \theta=(m-n) \alpha \\ \Rightarrow \alpha=\frac{\theta}{m-n}
समीकरण (1) में \alpha का मान रखने परः
r \cos \left[\theta-\frac{m \theta}{m-n}\right]=a\left(\cos \frac{n \theta}{n-n}\right)^{\frac{m}{n}} \\ \Rightarrow r \cos \left(\frac{n \theta}{m-n}\right)=a\left(\cos \frac{n \theta}{m-n}\right)^{\frac{n}{n}}\\ r=a\left(\cos \frac{n \theta}{m-n}\right)^{\left(\frac{m-n}{n}\right)}
अतः अन्वालोप का समीकरण होगाः
r^{\frac{n}{m-n}}=a^{\frac{n}{m-n}} \cos \left(\frac{n \theta}{m-n}\right)
Example:2.उन वृत्तों का अन्वालोप ज्ञात कीजिए जिसके व्यास परवलय y^2=4ax की द्विगुण कोटियाँ हैं।
(Find the envelope of the circles whose diameters are double ordinates of the parabola y^2=4ax .)
Solution:माना परवलय y^2=4ax की द्विगुण कोटियाँ \left(a t^2, 2 a t\right) व \left(a t^2,-2 a t\right) हैं।
व्यास रूप में वृत्त का समीकरणः
t के सापेक्ष आंशिक अवकलन करने परः
-4 a t x+4 a^2 t^3-8 a^2 t=0 \\ \Rightarrow -4 a t\left(x-a t^2+2 a\right)=0 \\ \Rightarrow x-a t^2+2 a=0 \\ \Rightarrow a t^2=x+2 a \\ \Rightarrow t^2=\frac{x+2 a}{a}\\t^2 का मान समीकरण (1) में रखने परः
x^2-2 a\left(\frac{x+2 a}{a}\right) x+a^2\left(\frac{x+2 a}{a}\right)^2+y^2-4 a^2\left(\frac{x+2 a}{a}\right)=0 \\ \Rightarrow x^2-2 x^2-4 a x+x^2+4 a x+4 a^2+y^2 -4 a x-8 a^2=0 \\ \Rightarrow y^2-4 a x-4 a^2=0 \\ \Rightarrow y^2=4 a x+4 a^2
अतः अन्वालोप का समीकरण होगाः
\Rightarrow y^2=4 a(x+a)
Example:3.उन वृत्तों का अन्वालोप ज्ञात कीजिए जो सदैव दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के केन्द्र से होकर जाते हैं और जिनके केन्द्र उसकी परिधि पर हैं।
(Find the envelope of the circle which pass through the centre of ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 and have their centres upon its circumference.)
Solution:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
माना दीर्घवृत्त का केन्द्र (0,0) तथा परिधि पर कोई बिन्दु (a \cos \theta, b \sin \theta) है।वृत्त जो दीर्घवृत्त के केन्द्र से होकर जाते हैं तथा जिसका केन्द्र परिधि पर हैः
त्रिज्या r= \sqrt{(a \cos \theta-0)^2+(b \sin \theta-0)^2} \\r =\sqrt{a^2 \cos ^2 \theta+b^2 \sin ^2 \theta}
वृत्त का समीकरणः
(x-a \cos \theta)^2+(y-b \sin \theta)^2=a^2 \cos ^2 \theta+b^2 \sin ^2 \theta \\ \Rightarrow x^2-2 a x \cos \theta+a^2 \cos ^2 \theta+y^2-2 b y \sin \theta+b^2 \sin ^2 \theta=a^2 \cos ^2 \theta+b^2 \sin ^2 \theta \\ \Rightarrow x^2+y^2=2 a x \cos \theta+2 b y \sin \theta \ldots(1)
प्राचल \theta के सापेक्ष आंशिक अवकलन करने परः
0=-2 a x \sin \theta+2 b y \cos \theta \ldots(2)
समीकरण (1) व (2) का वर्ग करके जोड़ने परः
\Rightarrow\left(x^2+y^2\right)^2=4 a^2 x^2 \cos ^2 \theta+4 b^2 y^2 \sin ^2 \theta+8a b x y \cos \theta \sin \theta+4 a^2 x^2 \sin ^2 \theta+4 b^2 y^2 \cos ^2 \theta-8 a b x y \sin \theta \cos \theta\\ \Rightarrow\left(x^2+y^2\right)^2=4 a^2 x^2\left(\cos ^2 \theta+\sin ^2 \theta\right)+4b^{2} y^{2}\left(\cos ^2 \theta+\sin ^2 \theta\right) \\ \Rightarrow \left(x^2+y^2\right)^2=4 a^2 x^2+4 b^2 y^2
अतः अन्वालोप का समीकरण होगाः
\left(x^2+y^2\right)^2=4\left(a^2 x^2+b^2 y^2\right)
Example:4.सिद्ध कीजिए कि दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के अर्धसंयुग्मी व्यासों के सिरों को मिलाने वाली रेखा सदैव दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{1}{2} को स्पर्श करती है।
(Show that the straight line joining the extremities of a pair of semiconjugate diameters of the ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 always touches the similar ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{1}{2}.)
Solution:माना दीर्घवृत्त के अर्धसंयुग्मी व्यासों के सिरों के निर्देशांक (a \cos \theta, b \sin \theta),[a \cos \left(\frac{\pi}{2}+\theta\right) =-a \sin \theta, b \sin \left(\frac{\pi}{2}+\theta\right)=b \cos \theta] हैं।
अतः (a \cos \theta, b \sin \theta) व (-a \sin \theta, b \cos \theta) को मिलाने वाली रेखा का समीकरण होगाः
y-b \sin \theta=\frac{b \cos \theta-b \sin \theta}{-a \sin \theta-a \cos \theta}(x-a \cos \theta) \\ \Rightarrow-a y \sin \theta-a y \cos \theta+a b \sin { }^2 \theta+a b \sin \theta \cos \theta=b x \cos \theta-a b \cos ^2 \theta-b x \sin \theta +a b \sin \theta \cos \theta \\ \Rightarrow b x \cos \theta-b x \sin \theta+a y \sin \theta+ a y \cos \theta=a b \\ \Rightarrow(b x+a y) \cos \theta+(a y-b x) \sin \theta=a b \ldots(1)
प्राचल \theta के सापेक्ष आंशिक अवकलन करने परः
समीकरण (1) व (2) का वर्ग करके जोड़ने परः
(b x+a y)^2 \sin ^2 \theta+(a y-b x)^2 \cos ^2 a -2(b x+a y)(a y-b x) \sin \theta \cos \theta +(b x+a y)^2 \cos ^2 \theta+(a y-b x)^2 \sin ^2 \theta +2(b x+a y)(a y-b x) \sin \theta \cos \theta=a^2 b^2 \\ \Rightarrow (b x+a y)^2\left(\sin ^2 \theta+\cos ^2 \theta\right)+(a y-b x)^2\left(\cos ^2 \theta+\sin ^2 \theta\right) =a^2 b^2 \\ \Rightarrow (b x+a y)^2+(a y-b x)^2=a^2 b^2 \\ \Rightarrow b^2 x^2+a^2 y^2+2 a b x y+a^2 y^2+b^2 x^2 -2 a b x y=a^2 b^2 \\ \Rightarrow 2 b^2 x^2+2 a^2 y^2=a^2 b^2 \\ \Rightarrow 2\left(\frac{b^2 x^2}{a^2 b^2}+\frac{a^2 y^2}{a^2 b^2}\right)=1 \\ \Rightarrow \frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{1}{2}
जो कि अभीष्ट अन्वालोप का समीकरण है।
Example:5.दीर्घवृत्त \frac{x^2}{\alpha^2}+\frac{y^2}{\beta^2}=1 पर स्थित किसी बिन्दु से दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 पर स्पर्श रेखाएँ खींची जाती हैं तो सिद्ध कीजिए कि सम्पर्क जीवा सदैव \frac{\alpha^2 x^2}{a^{4}}+\frac{\beta^2 y^2}{b^4}=1 को स्पर्श करती है।
(From any point on the ellipse \frac{x^2}{\alpha^2}+\frac{y^2}{\beta^2}=1,tangents are drawn to the ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=1.Show that the envelope of the chord of contact is \frac{\alpha^2 x^2}{a^{4}}+\frac{\beta^2 y^2}{b^4}=1 .)
Solution: \frac{x^2}{\alpha^2}+\frac{y^2}{\beta^2}=1 पर कोई बिन्दु (\alpha \cos \theta, \beta \sin \theta) है।
इस बिन्दु का \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के सापेक्ष सम्पर्क जीवा का समीकरणः
\frac{x}{a^2}(\alpha \cos \theta)+\frac{y}{b^2}(\beta \sin \theta)=1 \ldots(1)
समीकरण (1) का \theta के सापेक्ष आंशिक अवकलन करने परः
-\frac{\alpha x}{a^2} \sin \theta+\frac{\beta y}{b^2} \cos \theta=0 \ldots(2)
(1) व (2) का वर्ग करके जोड़ने परः
\frac{\alpha^2 x^2}{a^4} \cos ^2 \theta+\frac{\beta^2 y^2}{b^4} \sin ^2 \theta+\frac{2 \alpha \beta x y}{a^2 b^2} \sin \theta \cos \theta+\frac{\alpha^2 x^2}{a^4} \sin ^2 \theta +\frac{\beta^2 y^2}{b^4} \cos ^2 \theta-\frac{2 \alpha \beta x y}{a^2 b^2} \sin \theta \cos \theta =1 \\ \Rightarrow \frac{\alpha^2 x^2}{a^4}\left(\cos ^2 \theta+\sin ^2 \theta\right)+\frac{\beta^2 y^2}{b^4}\left(\sin ^2 \theta+\cos ^2 \theta\right)=1\\ \Rightarrow \frac{\alpha^2 x^2}{a^4}+\frac{\beta^2 y^2}{b^4}=1
जो कि अभीष्ट अन्वालोप है।
Example:6.सिद्ध कीजिए कि दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के सापेक्ष, दीर्घवृत्त \frac{x^2}{h^2}+\frac{y^2}{k^2}=1 पर स्थित बिन्दुओं के ध्रुवीय (polars) का अन्वालोप है।
(Show that the envelope of the polars of points on the ellipse \frac{x^2}{h^2}+\frac{y^2}{k^2}=1, with respect to the ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 is \frac{x^2 h^2}{a^4}+\frac{y^2 k^2}{b^4}=1)
Solution: \frac{x^2}{h^2}+\frac{y^2}{k^2}=1 पर कोई बिन्दु (h \cos \theta, k \sin \theta) है।इस बिन्दु \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 के सापेक्ष ध्रुवीय हैः
\frac{x(h \cos \theta)}{a^2}+\frac{y(k \sin \theta)}{b^2}=1 \ldots(1)
समीकरण (1) का \theta के सापेक्ष आंशिक अवकलन करने परः
\frac{-xh \sin \theta}{a^{2}}+\frac{yk \sin \theta}{a^{2}}=0 \ldots(2)
समीकरण (1) व (2) का वर्ग करके जोड़ने परः
\frac{x^2 h^2}{a^2} \cos ^2 \theta+\frac{y^2 k^2}{b^2} \sin ^2 \theta+\frac{2 x y h k}{a^2 b^2} \cos \theta \sin \theta+\frac{x^2 h^2}{a^2} \sin ^2 \theta+\frac{y^2 k^2}{b^2} \cos ^2 \theta-\frac{2 x y h k}{a^2 b^2} \cos \theta \sin \theta=1\\ \Rightarrow \frac{x^2 h^2}{a^2}\left(\cos ^2 \theta+\sin ^2 \theta\right)+\frac{y^2 k^2}{b^2}\left(\sin ^2 \theta+\cos ^2 \theta\right)=1 \\ \Rightarrow \frac{x^2 h^2}{a^2}+\frac{y^2 k^2}{b^2}=1
जो कि अभीष्ट अन्वालोप है।
Example:7.उन रेखाओं का अन्वालोप ज्ञात कीजिए जो निम्न-वक्रों की ध्रुवान्तर रेखाओं के सिरों पर समकोण बनाती हुई खींची गई होंः
(Find the envelopes of the straight lines at the right angles to the radii vectors of the following curves and drawn through their extremities):
Example:7(a). r=a+b \cos \theta
Solution: r=a+b \cos \theta
माना वक्र पर कोई बिन्दु P\left(r_1, \theta_1\right) है।
अब ध्रुवान्तर रेखा (radii vector) से समकोण बनाने वाली रेखा पर किसी बिन्दु Q के ध्रुवीय निर्देशांक \left(r,\theta\right) हो तो प्राचल PQ का समीकरण होगाः
r \cos \left(\theta-\theta_1\right)=r_{1} \\ \Rightarrow r \cos \left(\theta-\theta_1\right)=a+b \cos \theta_1 \\ \Rightarrow r \cos \theta \cos \theta_1+r \sin \theta \sin \theta_{1}=a+b \cos \theta_1 \\ \Rightarrow (r \cos \theta-b) \cos \theta_1+r \sin \theta \sin \theta_{1}=a \cdots(1)
प्राचल \theta_{1} के सापेक्ष आंशिक अवकलन करने परः
-(r \cos \theta-b) \sin \theta_{1}+r \sin \theta \cos \theta_{1}=0 \cdots(2)
समीकरण (1) व (2) का वर्ग करके जोड़ने परः
(r \cos \theta-b)^2 \cos ^2 \theta_{1}+r^2 \sin ^2 \theta \sin ^2 \theta_{1}+ 2 r(r \cos \theta-b) \sin \theta \cos \theta_{1} \sin \theta_{1}+(r \cos \theta-b)^2 \sin ^2 \theta_{1}+r^2 \sin ^2 \theta \cos ^2 \theta_{1} -2 r(r \cos \theta-b) \sin \theta \cos \theta_{1} \sin \theta_{1} =a^2 \\ \Rightarrow(r \cos \theta-b)^2\left(\cos ^2 \theta_{1}+\sin ^2 \theta_{1}\right)+r^2 \sin ^2 \theta\left(\sin ^2 \theta_{1}+\cos ^2 \theta_{1}\right)=a^2 \\ \Rightarrow(r \cos \theta-b)^2+r^2 \sin ^2 \theta=a^2 \\ \Rightarrow r^2 \cos ^2 \theta-2 b r \cos \theta+b^2+r^2 \sin ^2 \theta=a^2 \\ \Rightarrow r^2\left(\cos ^2 \theta+\sin ^2 \theta\right)-2 b r \cos \theta+b^2-a^2=0 \\ \Rightarrow r^2-2 b r \cos \theta+b^2-a^2=0
जो कि अभीष्ट अन्वालोप का समीकरण है।
Example:7(b). r=a e^{\cot \alpha}
Solution: r=a e^{\cot \alpha}
माना वक्र पर (r_{1}, \theta_{1}) किसी बिन्दु Q के ध्रुवीय निर्देशांक \left(r,\theta\right) हो तो PQ का समीकरण होगाः
r \cos \left(\theta-\theta_1\right)=r_1 \cdots(1)
P\left(r_1, \theta_1\right) वक्र पर है अतः
r_1=a e^{\theta_{1} \cot \alpha} \ldots(2)
(1) व (2) सेः
r \cos (\theta-\theta_{1})=a e^{\theta_{1} \cot \alpha} \ldots(3)
दोनों पक्षों का लघुगणक लेने परः
\log r+\log \cos (\theta-\theta_{1})=\log a+\theta_{1} \cot \alpha \\ \theta_{1} प्राचल के सापेक्ष आंशिक अवकलन करने परः
0+\frac{\sin (\theta-\theta_{1})}{\cos (\theta-\theta_{1})}=\cot \alpha \\ \Rightarrow \tan (\theta-\theta_{1})=\cot \alpha \\ \Rightarrow \tan (\theta-\theta_{1})=\tan \left ( \frac{\pi}{2}-\alpha \right ) \\ \Rightarrow \theta-\theta_{1}=\frac{\pi}{2}-\alpha \\ \Rightarrow \theta_{1}=\theta-\frac{\pi}{2}+\alpha \\ \theta_{1} का मान समीकरण (3) में रखने परः
r \cos \left ( \theta-\theta+\frac{\pi}{2}-\alpha \right )=e^{\left ( \theta-\frac{\pi}{2}+\alpha \right ) \cot \alpha} \\ \Rightarrow r \sin \alpha=e^{\left(\alpha-\frac{\pi}{2}\right) \cot \alpha} \cdot e^{\theta \cos \alpha}
जो कि अभीष्ट अन्वालोप का समीकरण है।
Example:7(c). r^n=a^n \cos n \theta
Solution: r^n=a^n \cos n \theta
माना वक्र पर कोई बिन्दु P\left(r_1, \theta_1\right) है।
अब ध्रुवान्तर रेखा (radii vector) से समकोण बनाने वाली रेखा पर किसी बिन्दु Q के ध्रुवीय निर्देशांक हो तो PQ का समीकरण होगाः
r \cos (\theta-\theta_{1})=r_{1} \cdots(1)
P\left(r_1, \theta_1\right) वक्र पर है अतः
(1) व (2) सेः
r_{1}^n=a^n \cos n \theta_{1} \\ r_1=a \cos ^{\frac{1}{n}} n \theta_1 \cdots(2)
दोनों पक्षों का लघुगणक लेने परः
\log r+\log \cos (\theta-\theta)=\log a+\frac{1}{n} \log \cos n \theta_{1}
प्राचल \theta_{1} के सापेक्ष आंशिक अवकलन करने परः
0+\frac{\sin (\theta-\theta_{1})}{\cos (\theta-\theta_{1})}=0-\frac{1}{n} \times n \frac{\sin n \theta 1}{\cos n \theta 1} \\ \Rightarrow \tan (\theta-\theta_{1})=-\tan n \theta_{1} \\ \Rightarrow \tan (\theta-\theta_{1})=\tan (-n \theta_{1}) \\ \Rightarrow \theta-\theta_{1}=-n \theta_{1} \\ \Rightarrow \theta_{1}-n \theta_{1}=\theta \\ \Rightarrow \theta_{1}=\frac{\theta}{1-n} \\ \theta_{1} का मान समीकरण (3) में रखने परः
r \cos \left(\theta-\frac{\theta}{1-n}\right)=a \cos^{\frac{1}{n}} \left(\frac{n \theta}{1-n}\right) \\ \Rightarrow r \cos \left(\frac{n \theta}{1-n}\right)=a \cos ^{\frac{1}{n}}\left(\frac{n \theta}{1-n}\right) \\ \Rightarrow r=a \cos ^{\frac{1-n}{n}}\left(\frac{n \theta}{1-n}\right) \\ \Rightarrow r^{\frac{n}{1-n}}=a^{\frac{n}{1-n}} \cos \left(\frac{n \theta}{1-n}\right)
जो कि अभीष्ट अन्वालोप का समीकरण है।
Example:8.उन वृत्तों का अन्वालोप ज्ञात कीजिए जो निम्न वक्रों की ध्रुवान्तर रेखाओं को व्यास मानकर खींचे गए हैंः
(Find the envelope of the circles described on the radii vectors of the following curves as diameters):
Example:8(a). r=2 a \cos \theta
Solution: r=2 a \cos \theta
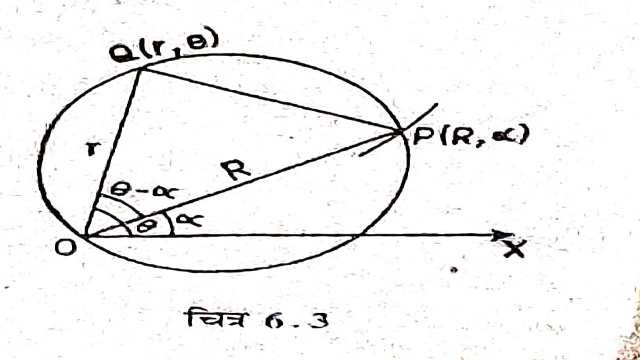
माना कि दिए हुए वक्र पर कोई बिन्दु P(R,\alpha) है तो
अब OP को व्यास मानकर वृत्त खींचा तथा यह मान लिया कि इस पर कोई बिन्दु Q(r, \theta) है।अब \triangle OPQ में \angle OQP=\frac{\pi}{2} \\ O Q=O P \cos (\theta-\alpha) \\ \Rightarrow r=R \cos (\theta-\alpha) \cdots(2)
यह उस वृत्त का समीकरण है जिसका व्यास OP है।R का मान (1) से (2) में रखने परः
r=2 a \cos \alpha \cos (\theta-\alpha) \cdots(3)
दोनों पक्षों का लघुगणक लेने परः
\log r=\log 2+\log a+\log \cos \alpha+\log \cos (\theta-\alpha)
प्राचल \alpha के सापेक्ष आंशिक अवकलन करने परः
0=0+0-\frac{\sin \alpha}{\cos \alpha}+\frac{\sin (\theta-\alpha)}{\cos (\theta-\alpha)} \\ \Rightarrow \tan \alpha=\tan (\theta-\alpha) \\ \Rightarrow \alpha=\theta-\alpha \Rightarrow \alpha=\frac{\theta}{2} \\ \alpha का मान (3) में रखने परः
r=2 a \cos \frac{\theta}{2} \cos \frac{\theta}{2} \\ \Rightarrow r=(1+\cos \theta)
Example:8(b). \frac{l}{r}=1+e \cos \theta
Solution: \frac{l}{r}=1+e \cos \theta
माना कि दिए हुए वक्र पर कोई बिन्दु P(R,\alpha) है तो
\Rightarrow R=\frac{l}{1+e \cos \alpha} \cdots(1)
अब OP को व्यास मानकर वृत्त खींचा तथा यह मान लिया कि इस पर कोई बिन्दु Q(r, \theta) है।अब \triangle OPQ में \angle OQP=\frac{\pi}{2} \\ OQ=O P \cos (\theta-\alpha) \\ \Rightarrow r=R \cos (\theta-\alpha) \cdots(2)
यह उस वृत्त का समीकरण है जिसका व्यास OP है।R का मान (1) से (2) में रखने परः
r=\frac{l}{1+e \cos \alpha} \cos (\theta-\alpha) \\ \Rightarrow r+e r \cos \alpha=l \cos \theta \cos \alpha+l \sin \theta \sin \alpha \\ (l \cos \theta-e r) \cos \alpha+l \sin \theta \sin \alpha=r \ldots(3)
प्राचल \alpha के सापेक्ष आंशिक अवकलन करने परः
-(l \cos \theta-e r) \sin \alpha+l \sin \theta \cos \alpha=0 \cdots(4)
(3) व (4) का वर्ग करके जोड़ने परः
(l \cos \theta-e r)^2 \cos ^2 \alpha+l^2 \sin ^2 \theta \sin ^2 \alpha+2(l \cos \theta-e r) l \sin \theta \cos \alpha \sin \alpha+(l \cos \theta-e r)^2 \sin ^2 \alpha+l^2 \sin ^2 \theta \cos ^2 \alpha-2(l \cos \theta-e r) l \sin \theta \cos \alpha \sin \alpha=r^{2} \\ \Rightarrow (l \cos \theta-e r)^2\left(\cos ^2 \alpha+ \sin ^2 \alpha \right) +l^2 \sin ^2 \theta \left(\sin^{2} \alpha+\cos ^2 \alpha\right)=r^2 \\ \Rightarrow (l \cos \theta-e r)^2+l^2 \sin ^2 \theta=r^2 \\ \Rightarrow l^2 \cos ^2 \theta-2 l e r \cos \theta+e^2 r^2+l^2 \sin ^2 \theta=r^{2} \\ \Rightarrow \left(e^2-1\right) r^2-2 l e r \cos \theta+ l^2\left(\sin ^2 \theta+\cos ^2 \theta\right)=0 \\ \Rightarrow\left(e^2-1\right) r^2-2 l e r \cos \theta+l^2=0
जो कि अभीष्ट अन्वालोप का समीकरण है।
उपर्युक्त उदाहरणों के द्वारा गणित में अन्वालोप (Envelope in Mathematics),एक वक्र का अन्वालोप कैसे ज्ञात करें? (How to Find Envelope of a Curve) को समझ सकते हैं।
3.गणित में अन्वालोप पर आधारित सवाल (Questions Based on Envelope in Mathematics):
(1.)उन रेखाओं का अन्वालोप ज्ञात कीजिए जो कार्डिआइड r=a(1+\cos \theta) की ध्रुवान्तर रेखाओं के सिरों से उन पर समकोण बनाती हुई खींची जाए
(Find the envelope of a straight line draw at right angles to the ends of the radii vectors of the cardiod r=a(1+\cos \theta).)
(2.)उन वृत्तों का समीकरण ज्ञात कीजिए जो वक्र r^n=a^n \cos n \theta की ध्रुवान्तर रेखाओं को व्यास मानकर खींचे गए हैं।
(Find the envelope of the circle described on the radii vectors of the curve r^n=a^n \cos n \theta as diameter.)
उपर्युक्त सवालों को हल करने पर गणित में अन्वालोप (Envelope in Mathematics),एक वक्र का अन्वालोप कैसे ज्ञात करें? (How to Find Envelope of a Curve?) को ठीक से समझ सकते हैं।
Also Read This Article:-Equation of Right Circular Cylinder
4.गणित में अन्वालोप (Envelope in Mathematics),एक वक्र का अन्वालोप कैसे ज्ञात करें? (How to Find Envelope of a Curve?) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.वक्रों का कुल किसे कहते हैं? (What is the family of curves?):
Solution:सामान्यतः यदि किसी वक्र का समीकरण f(x, y, \alpha)=0 है तथा इसमें अचर \alpha को भिन्न-भिन्न स्वेच्छ (arbitrary) संख्यात्मक मान प्रदान करे जाए तो के भिन्न-भिन्न \alpha मान के लिए भिन्न-भिन्न वक्र प्राप्त होंगे तथा इन सभी वक्रों को वक्रों का कुल (family of curves) कहते हैं।
प्रश्न:2.वक्र का कुल प्राचल किसे कहते हैं? (What is the parameter of family of curves?):
उत्तरःउपर्युक्त प्रश्न एक के उत्तर में वक्रों का कुल में \alpha के \alpha , मान के लिए हमको कुल का एक सदस्य प्राप्त होगा।अतः प्रत्येक वक्र कुल के सदस्य के लिए \alpha का मान अचर होता है और इसे वक्र कुल का प्राचल कहते हैं।
प्रश्न:3.अन्वलोप की द्वितीय परिभाषा क्या है? (What is the second definition of envelope?):
उत्तरःयदि f(x, y, \alpha)=0 एक वक्र कुल को प्रदर्शित करे जिसका प्राचल \alpha है तथा यदि वक्र f(x, y, \alpha)=0 और f(x, y, \alpha+\delta \alpha)=0 का प्रतिच्छेद बिन्दु इस प्रकार हो कि जब \delta \alpha \rightarrow 0 तब यह एक निश्चित बिन्दु P की ओर प्रवृत्त होता है।तब प्रतिच्छेदन बिन्दु P का बिन्दुपथ (locus) (\alpha के चर मानों के लिए) वक्र कुल का अन्वालोप (envelope) कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा गणित में अन्वालोप (Envelope in Mathematics),एक वक्र का अन्वालोप कैसे ज्ञात करें? (How to Find Envelope of a Curve?) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Envelope in Mathematics
गणित में अन्वालोप (Envelope in Mathematics)
Envelope in Mathematics
गणित में अन्वालोप (Envelope in Mathematics) जो किसी वक्र कुल (family of curves) के
प्रत्येक सदस्य को स्पर्श करता है तथा स्वयं प्रत्येक बिन्दु पर वक्र कुल के किसी न किसी सदस्य