अवकलन गणित में द्विक बिन्दु (Double Points in Differential Calculus):यदि वक्र का ऐसा बिन्दु हो जिससे वक्र की केवल दो शाखाएँ ही गुजरती हैं तो उस बिन्दु को द्विक बिन्दु (Double Points) कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Point of Inflexion in Calculus

2.अवकलन गणित में द्विक बिन्दु के साधित उदाहरण (Double Points in Differential Calculus Solved Examples):
निम्नलिखित वक्रों पर द्विक बिन्दुओं को निर्धारित कीजिए एवं उनकी प्रकृति को भी निश्चित कीजिएः

(Determine the existence and examine the nature of the double points on the following curves):
Example:1. $y^2\left(a^2+x^2\right)=x^2\left(a^2-x^2\right)$
Solution: $y^2\left(a^2+x^2\right)=x^2\left(a^2-x^2\right)$
यहाँ $f(x, y)=a^2 y^2+x^2 y^2-a^2 x^2+x^4=0 \\ \frac{\partial f}{\partial x}=2 x y^2-2 a^2 x+4 x^3$
तथा $\frac{\partial f}{\partial y}=2 a^2 y+2 x^2 y$
द्विक बिन्दुओं के लिए $\frac{\partial f}{\partial x}=0, \frac{\partial f}{\partial y}=0$ तथा f=0 होता है।

$2 x y-2 a^2 x+4 x^3=0 \\ \Rightarrow 2 x\left(y-a^2+2 x^2\right)=0 \\ x=0, y^2-a^2+4 x^2=0 \cdots(1) \\ 2 a^2 y+2 x^2 y=0 \\ \Rightarrow y\left(a^2+x^2\right)=0 \\ y=0, a^2+x^2=0 \cdots(2)$
(1) व (2) सेः

$y^2-a^2-4 a^2=0 \Rightarrow y=\sqrt{5} a$
(1) में रखने पर : $x=\sqrt{-a^2}$ काल्पनिक है।
अतः इन बिन्दुओं में से (0,0) वक्र पर है जो कि वक्र की समीकरण को सन्तुष्ट करता है।अतः वक्र का बिन्दु (0,0) केवल द्विक बिन्दु है।
पुनः $\frac{\partial^2 f}{\partial x^2}=2 y^2-2 a^2+12 x^2 \\ \left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,0)} =2(0)^2-2 a^2+12(0)^2 \\ =-2 a^2 \\ \frac{\partial^2 f}{\partial x \partial y}=4 x y \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(0,0)}=0 \\ \frac{\partial^2 f}{\partial y^2}=2 a^2+2 x^2 \\ \Rightarrow\left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,0)}=2 a^2 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)>\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow 0 > \left(-2 a^2\right)\left(2 a^2\right) \\ \Rightarrow 0>-4 a^2$
फलतः मूलबिन्दु (0,0) पर नोड (node) है।
Example:2. $y^2=b x \sin \left(\frac{x}{a}\right)$
Solution: $y^2=b x \sin \left(\frac{x}{a}\right)$
यहाँ $f(x, y)=y^2-b x \sin \left(\frac{x}{a}\right)=0 \\ \frac{\partial f}{\partial x}=-b \sin \left(\frac{x}{a}\right)-\frac{b}{a}x \cos \left(\frac{x}{a}\right), \frac{\partial f}{\partial y}=2 y$
द्विक बिन्दुओं के लिए $\frac{\partial f}{\partial x}=0, \frac{\partial f}{\partial y}=0 \\ -b \sin \frac{x}{a}-\frac{b x}{a} \cos \left(\frac{x}{a}\right)=0 \Rightarrow x=0 \\ 2 y=0 \quad \Rightarrow y=0 \\ (0,0)$
अतः (0,0) बिन्दु प्राप्त होता है जो कि वक्र पर भी विद्यमान है।अतः (0,0) द्विक बिन्दु है।
$\frac{\partial^2 f}{\partial x^2}=-\frac{b}{a} \cos \left(\frac{x}{a}\right)-\frac{b}{a} \cos \left(\frac{x}{a}\right) + \frac{b x}{a^2} \sin \left(\frac{x}{a}\right) \\ \left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,0)}=-\frac{b}{a} \cos 0-\frac{b}{a} \cos 0+0 \\ \Rightarrow \left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,0)}=-\frac{2 b}{a} \\ \frac{\partial^2 f}{\partial x \partial y}=0, \quad \frac{\partial^2 f}{\partial y^{2}}=2 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2 > \left(\frac{\partial^2 f}{\partial x^2}\right) \left(\frac{\partial^2 f}{\partial y^2}\right)$ [जब b व a एक ही चिन्हों के हों]

$0>-\frac{2 b }{a} \times 2 \Rightarrow 0<-\frac{4 b}{a}$
अतः b व a एक चिन्हों के हों तो मूलबिन्दु पर एक नोड है।
$\left(\frac{\partial^2 f}{\partial x \partial y}\right)<\left(\frac{\partial^2 f}{\partial x^{2}}\right) \left(\frac{\partial^2 f}{\partial y^{2}}\right)$ [जब b व a विपरीत चिन्हों के हों]

$\Rightarrow 0<-\frac{2 b}{a} \times 2 \Rightarrow 0<-\frac{4 b}{a}$
अतः b व a विपरीत चिन्हों के होने पर मूलबिन्दु पर एक वियुक्त बिन्दु है।
Example:3. $x^4+y^3+2 x^2+3 y^2=0$
Solution: $x^4+y^3+2 x^2+3 y^2=0$
यहाँ $f(x, y)=x^4+y^3+2 x^2+3 y^2=0 \\ \frac{\partial f}{\partial x}=4 x^3+4 x, \frac{\partial f}{\partial y}=3 y^2+6 y$
अब द्विक बिन्दु के अस्तित्व के लिए
$\frac{\partial f}{\partial x}=0 तथा \frac{\partial f}{\partial y}=0 \\ \Rightarrow 4 x^3+4 x=0 \Rightarrow x =0 \\ 3 y^2+6 y=0 \Rightarrow y=0$
अतः हमें (0,0) बिन्दु प्राप्त होता है जो कि वक्र पर विद्यमान है।अतः (0,0) द्विक बिन्दु है।

$\frac{\partial^2 f}{\partial x^2}=12 x^2+4 \Rightarrow\left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,0)}=4 \\ \frac{\partial^2 f}{\partial x \partial y}=0 , \frac{\partial^2 f}{\partial y^2}=6 y+6 \Rightarrow \left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,0)}=6 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2 <\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \Rightarrow 0<4 \times 6 \\ \Rightarrow 0<24$
अतः मूलबिन्दु पर वियुक्त बिन्दु है।
Example:4. $y(y-6)=x^2(x-2)^3-9$
Solution: $y(y-6)=x^2(x-2)^3-9$
यहाँ $f(x, y)=y^2-6 y-x^5+6 x^4-12 x^3+8 x^2+9=0 \\ \frac{\partial f}{\partial x}=-5 x^4+24 x^3-36 x^2+16 x \\ \frac{\partial f}{\partial y}=2 y-6$
अब द्विक बिन्दु के अस्तित्व के लिए
$\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ -5 x^4+24 x^3-36 x^2+16 x=0 \\ \Rightarrow -5 x\left(x^3-24 x^2+36 x-16\right)=0 \\ \Rightarrow x=0, x^3-24 x^2+36 x-16=0 \\ 2 y-6=0 \Rightarrow y=3$
y का मान दिए हुए वक्र के समीकरण में रखने परः

$(3)^2-6 \times 3-x^5+6 x^4-12 x^3+8 x^2+9=0 \\ \Rightarrow 9-18-x^5+6 x^4-12 x^3+8 x^2+9=0 \\ \Rightarrow-x^2\left(x^3-6 x^2+12 x-8\right)=0 \\ \Rightarrow x^3-2 x^2-4 x^2+8 x+4 x-8=0 \\ \Rightarrow x^2(x-2)-4 x(x-2)+4(x-2)=0 \\ \Rightarrow (x-2)\left(x^2-4 x+4\right)=0 \\ \Rightarrow(x-2)^3=0 \Rightarrow x=2$
जब x=0 तो $y^2-6 y+9=0 \\ \Rightarrow(y-3)^2=0 \Rightarrow y=3$
अतः दो बिन्दु (2,3) व (0,3) प्राप्त होते हैं जो कि वक्र पर विद्यमान हैं।फलतः (2,3),(0,3) द्विक बिन्दु हैं।

$\frac{\partial^2 f}{\partial x^2}=-20 x^3+72 x^2-72 x+16 \\ \left(\frac{\partial^2 f}{\partial x^2} \right)_{(2,3)} = -20(2)^3+72(2)^2-72 \times 2+16 \\ =-160+288-144+16 \\ \Rightarrow \left(\frac{\partial^2 f}{\partial x^2}\right)_{(2,3)}=0 \\ \frac{\partial^2 f}{\partial x \partial y}=0 \quad \Rightarrow\left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(2,3)}=0 \\ \frac{\partial^2 f}{\partial y^2}=2 \Rightarrow\left(\frac{\partial^2 f}{\partial y^2}\right)_{(2,3)}=2 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2=\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow(0)^2=0(2) \Rightarrow 0=0$
अतः बिन्दु (2,3) पर उभयाग्र है।
अब बिन्दु (0,3) परः

$\left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,3)}=16,\left(\frac{\partial^2 f}{\partial x \partial y} \right)_{(0,3)} =0,\left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,3)}=2 \\ \Rightarrow\left(\frac{\partial^2 f}{\partial x y}\right)^2 < \left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow(0)^2 = 16 \times 2 \Rightarrow 0< 32$
अतः बिन्दु (0,3) पर वियुक्त बिन्दु है।
मूलबिन्दु को (2,3) पर स्थानान्तरित करने परः

$(y+3)(y+3-6)=(x+2)^2 \cdot (x+2-2)^3-9 \\ \Rightarrow y^2-9=(x+2)^2 x^3-9 \\ \Rightarrow y= \pm\left[x^3(x+2)^2\right]^{\frac{1}{2}}$
समीकरण की न्यूनतम घात के पदों को शून्य के बराबर रखने पर $y^2=0$ जिससे दो स्पर्श रेखाएँ प्राप्त होती हैं।y का मान एक धनात्मक और दूसरा ऋणात्मक है।
अतः (2,3) पर प्रथम प्रकार का उभयाग्र है।
Example:5. $(x+y)^3=\sqrt{2}(y-x+2)^2$
Solution: $(x+y)^3=\sqrt{2}(y-x+2)^2$
यहाँ $f(x, y)=x^3+3 x^2 y+3 x y^2+y^3-\sqrt{2} y^2-\sqrt{2} x^2+2 \sqrt{2} x y+4 \sqrt{2} x-4 \sqrt{2} y-4 \sqrt{2}=0 \\ \frac{\partial f}{\partial x}=3 x^2+6 x y+3 y^2-2 \sqrt{2} x+2 \sqrt{2} y+4 \sqrt{2} \\ \frac{\partial f}{\partial y}=3 x^2+6 x y+3 y^2-2 \sqrt{2} y+2 \sqrt{2} x-4 \sqrt{2}$
द्विक बिन्दुओं के अस्तित्व के लिए $\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ 3 x^2+6 x y+3 y^2-2 \sqrt{2} x+2 \sqrt{2} y+4 \sqrt{2}=0 \cdots(1) \\ 3 x^2+6 x y+3 y^2-2 \sqrt{2} y+2 \sqrt{2} x-4 \sqrt{2}=0 \cdots(2)$
समीकरण (1) व (2) को जोड़ने परः

$6 x^2+12 x y+6 y^2=0 \Rightarrow x^2+2 x y+y^2=0 \\ \Rightarrow(x+y)^2=0 \Rightarrow x=-y$
समीकरण (1) में x=-y रखने परः
$3 y^2-6 y^2+3 y^2+2 \sqrt{2} y+2 \sqrt{2} y+4 \sqrt{2}=0 \\ \Rightarrow 4 \sqrt{2} y+4 \sqrt{2}=0 \Rightarrow 4 \sqrt{2}(y+1)=0 \\ \Rightarrow y=-1$ अतः x=1
अतः (1,-1) बिन्दु प्राप्त होता है जो वक्र पर विद्यमान है।फलतः (1,-1) द्विक बिन्दु है।

$\frac{\partial^2 f}{\partial x^2}=6 x+6 y-2 \sqrt{2} \Rightarrow\left(\frac{\partial^2 f}{\partial x^2}\right)_{(1,-1)}=6-6-2 \sqrt{2}=-2 \sqrt{2} \\ \frac{\partial^2 f}{\partial y^{2}}=6 x+6 y-2 \sqrt{2} \Rightarrow\left(\frac{\partial^2 f}{\partial y^2}\right)_{(1,-1)}= 6-6-2 \sqrt{2}=-2 \sqrt{2} \\ \frac{\partial^2 f}{\partial x \partial y}=6 x+6 y+2 \sqrt{2} \Rightarrow\left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(1,-1)}=6-6+2 \sqrt{2}=2 \sqrt{2} \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2=\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow(2 \sqrt{2})^2=(-2 \sqrt{2})(-2 \sqrt{2}) \Rightarrow 8= 8$
अतः बिन्दु (1,-1) पर उभयाग्र है।
मूलबिन्दु को (1,-1) पर स्थानान्तरित करने परः

$\Rightarrow(x+1+y-1)^3=\sqrt{2}(y-1-x-1+2)^2 \\ \Rightarrow(x+y)^3=\sqrt{2}(y-x)^2$
न्यूनतम घात के पदों को शून्य के बराबर रखने पर $(y-x)^{2}=0$ , दो वास्तविक और संपाती स्पर्श रेखाएँ हैं।अतः नया मूलबिन्दु या तो उभयाग्र है या वियुक्त बिन्दु
माना $y-x=P \Rightarrow y=P+x \\ (2 x+p)^3=\sqrt{2} P^2 \\ \Rightarrow P^3+P^2(6 x-\sqrt{2})+12 x^2 P+8 x^3=0$
उच्चतम घात $P^3$ को नगण्य मानने परः

$(6 x-\sqrt{2}) P^2+12 x^2 P+8 x^2=0 \\ \Rightarrow P=\frac{-12 x^2 \pm \sqrt{\{144 x-32x^{3}(6x-\sqrt{2})\}}}{2(6 x-\sqrt{2})} \\ =\frac{-6 x^2 \pm \sqrt{\left(8 \sqrt{2} x^3-12 x^{4}\right)}}{(6 x-\sqrt{2})} \\ -12 x^{4}$ को नगण्य मानने परः

$\Rightarrow P=\frac{-6 x^2+2(\sqrt{2 x})^{\frac{3}{2}}}{(6 x-\sqrt{2})}$
यदि x छोटा है तो $x^{\frac{3}{2}}, x^2$ से बड़ा है तथा x धनात्मक है तो P वास्तविक और विपरीत चिन्ह के होंगे।
अतः नए मूलबिन्दु पर प्रथम प्रकार का एकल उभयाग्र है।

Double Points in Differential Calculus

Example:6. $x^3+y^3-3 a x y=0$
Solution: $x^3+y^3-3 a x y=0$
यहाँ $f(x, y)=x^3+y^3-3 a x y=0 \\ \frac{\partial f}{\partial x}=3 x^2-3 a y, \frac{\partial f}{\partial y}=3 y^2-3 a x$
द्विक बिन्दुओं के अस्तित्व के लिए $\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ 3 x^2-3 a y=0 \cdots(1) \\ 3 y^2-3 a x=0 \cdots(2)$

समीकरण (1) व (2) को घटाने परः

$3 x^2-3 y^2-3 a y+3 a x=0 \\ \Rightarrow x^2-y^2-a y+a x=0 \\ \Rightarrow (x-y)(x+y)+a(x-y)=0 \\ \Rightarrow (x-y)(x+y+a)=0 \\ \Rightarrow x-y=0, x+y+a=0 \\ \Rightarrow x=y$
x=y समीकरण (1) में रखने परः

$3 y^2-3 a y=0 \Rightarrow y(y-a)=0 \\ \Rightarrow y = 0, a \\ x=0, a$
अतः (0,0),(a,a) बिन्दु प्राप्त होते हैं जिनमें (0,0) वक्र पर विद्यमान है।फलतः (0,0) द्विक बिन्दु है।

$\frac{\partial^2 f}{\partial x^2}=6 x \Rightarrow\left(\frac{\partial^2 f}{\partial x^{2}}\right)_{(0,0)}=0 \\ \frac{\partial^2 f}{\partial y^2}=6 y \Rightarrow\left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,0)}=0 \\ \frac{\partial^2 f}{\partial x \partial y}=-3 a \Rightarrow\left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(0,0)} =-3 a \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2>\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow(-3 a)^2>(0)(0) \Rightarrow 9 a^2>0$
अतः बिन्दु (0,0) पर नोड है।
Example:7. $x^4-2 a y^3-3 a^2 y^2-2 a^2 x^2+a^4=0$
Solution: $x^4-2 a y^3-3 a^2 y^2-2 a^2 x^2+a^4=0$
यहाँ $f(x, y)=x^4-2 a y^3-3 a^2 y^2-2 a^2 x^2+a^4=0 \\ \frac{\partial f}{\partial x}=4 x^3-4 a^2 x, \frac{\partial f}{\partial y}=-6 a y^2-6 a^2 y$
द्विक बिन्दुओं के अस्तित्व के लिए $\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ 4 x^3-4 a^2 x=0 \Rightarrow 4 x\left(x^2-a^2\right)=0 \Rightarrow x=0, \pm a \\ -6 a y^2-6 a^2 y=0 \Rightarrow-6 a y(y+a)=0 \Rightarrow y=0,-a$
अतः बिन्दु (0,0),(0,-a),(a,0),(a,-a),(-a,a),(-a,-a) प्राप्त होते हैं।इनमें से (a,0),(-a,0) व (0,-a) वक्र के समीकरण को सन्तुष्ट करते हैं।फलतः (a,0),(-a,0) व (0,-a) द्विक बिन्दु हैं।

$\frac{\partial^2 f}{\partial x^2}=12 x^2-4 a^2 \Rightarrow\left(\frac{\partial^2}{\partial x^2}\right)_{(a, 0)}=12 a^2-4 a^2=8 a^2 \\ \frac{\partial^2 f}{\partial y^2}=-12 a y-6 a^2 \Rightarrow \left(\frac{\partial^2 f}{\partial y^2}\right)_{(a,0)}=-6 a^2 \\ \frac{\partial^2 f}{\partial x \partial y}=0 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^{2} > \left(\frac{\partial^2 f}{\partial x^2}\right) \left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow(0)^2<\left(8 a^2\right)\left(-6 a^2\right) \\ \Rightarrow 0>-48 a^4$
बिन्दु (a,0) पर नोड है।

$\left(\frac{\partial^2 f}{\partial x^{2}}\right)_{(-a,0)}=12 a^2-4 a^2=8 a^2 \\ \left(\frac{\partial^2 f}{\partial y^2}\right)_{(-a,0)}=12 a^2-6 a^{2}=-6 a^{2} \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(-a,0)}=0 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2>\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right)\\ \Rightarrow (0)^{2}<\left(8 a^2\right)\left(-6 a^2\right) \\ \Rightarrow 0 < -48 a^{4}$
अतः बिन्दु (-a,0) पर नोड है।

$\left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,-a)}=12(0)^2-4 a^2=-4 a^2 \\ \left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,-a)}=-6 a^2=-6 a^2 \\ \left(\frac{\partial^2 x}{\partial x \partial y}\right)_{(0,-a)}=0 \\ \left(\frac{\partial^2 f}{\partial x y}\right)^2 < \left(\frac{\partial^2 f}{\partial x^2}\right) \left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow(0)^2<\left(-4 a^2\right)\left(-6 a^2\right) \\ \Rightarrow 0<24 a^{2}$
अतः (0,-a) पर वियुक्त बिन्दु है।
Example:8. $x^2 y^2-(a+y)^2\left(b^2-y^2\right)$
Solution: $x^2 y^2-(a+y)^2\left(b^2-y^2\right)$
यहाँ $f(x, y)=y^4+x^2 y^2+2 a y^3+a^2 y^2-b^2 y^2-2 a b^2 y-a^2 b^2=0 \\ \frac{\partial f}{\partial x}=2 x y^2 \\ \frac{\partial f}{\partial y}=4 y^3+2 x^2 y+6 a y^2+2 a^2 y-2 b^2 y-2 a b^2$
अब द्विक बिन्दुओं के अस्तित्व के लिए
$\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ 2 x y^2=0 \Rightarrow x=0, y=0 \\ 4 y^3+2 x^2 y+6 a y^2+2 a^2 y-2 b^2 y-2 a b^2=0$
x=0 दिए हुए वक्र के समीकरण में रखने पर y=-a
(0,-a)
अतः बिन्दु (0,-a) प्राप्त होता है जो वक्र पर विद्यमान है।फलतः (0,-a) द्विक बिन्दु है।
$\frac{\partial^2 f}{\partial x^2}=2 y^2 \\ \frac{\partial^2 f}{\partial x \partial y}=4 x y \\ \frac{\partial^{2} f}{\partial y^2} =12 y^2+2 x^2+12 a y+2 a^2-2 b^2 \\ \left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,-a)} =2a^{2} \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(0,-a)}=0 \\ \left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,-a)}=12 a^2-12 a^{2}+2 a^2-2 b^2 \\ \Rightarrow \left(\frac{\partial^2 f}{\partial y^2} \right)_{(0,-a)} =2a^{2}-2b^{2}\\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2> \left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right)$ [यदि b>a]

अतः $(0)^2>2 a^2\left(2 a^2-2 b^2\right)$ [यदि b>a]
b>a पर नोड होगा।

$\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2=\left(\frac{\partial^2 f}{\partial x^2}\right) \left(\frac{\partial^2 f}{\partial y^2}\right)$ [यदि b=a]

$\Rightarrow(0)^2=2 a^2\left(2 a^2-2 a^2\right)=0$
अतः b=a पर एक उभयाग्र होगा।
यदि b<a
$\left(\frac{\partial^2 f}{\partial x \partial y}\right)<\left(\frac{\partial^2 f}{\partial x^2}\right) \left(\frac{\partial^2 f}{\partial y^2}\right)$ [यदि b<a]
अतः b<a पर वियुक्त बिन्दु है।
Example:9. $y^3=x^3+a x^2$
Solution: $y^3=x^3+a x^2$
यहाँ $f(x, y)=y^3-x^3-a x^2=0 \\ \frac{\partial f}{\partial x}=-3 x^2-2 a x, \frac{\partial f}{\partial y}=3 y^2$
अब द्विक बिन्दुओं के अस्तित्व के लिए
$\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ -3 x^2-2 a x=0 \Rightarrow -x(3 x+2 a)=0 \\ \Rightarrow x=0,-\frac{2 a}{3}$ तथा $3 y^2=0 \Rightarrow y=0$
अतः $(0,0),\left(-\frac{2 a}{3}, 0\right)$ बिन्दु प्राप्त होते हैं।इनमें (0,0) वक्र पर विद्यमान है।फलतः (0,0) द्विक बिन्दु है।

$\frac{\partial^2 f}{\partial x^2}=-6 x-2 a, \frac{\partial^2 f}{\partial y^2}=6y \\ \left(\frac{\partial^2 f}{\partial x^2}\right)_{(0,0)}=-2 a, \left(\frac{\partial^2 f}{\partial y^2}\right)_{(0,0)}=0 \\ \frac{\partial^2 f}{\partial x \partial y}=0 \\ \Rightarrow\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2= \left( \frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow (0)^2=(-2 a)(0) \Rightarrow 0=0$
अतः मूलबिन्दु (0,0) पर उभयाग्र है।
वक्र के समीकरण में x=P रखने पर तथा उच्चतम घात को नगण्य मानने पर

$y^3=p^3+a p^2 \\ \Rightarrow a p^2+o p-y^3=0$
विविक्तिकर $B^2-4 A C=0^2+4 a y^3$
जो केवल y के चिन्ह पर निर्भर करता है।मूलों का गुणनफल= $-\frac{y^3}{a}$ जो y के धनात्मक होने पर ऋणात्मक है जिससे प्रदर्शित होता है कि मूल विपरीत चिन्हों के हैं अतः प्रथम प्रकार का उभयाग्र है।
Example:10. $y^2=(x-1)(x-2)^2$
Solution: $y^2=(x-1)(x-2)^2$
यहाँ $f(x, y)=y^2-x^3+5 x^2-8 x+4 \\ \frac{\partial f}{\partial x}=-3 x^2+10 x-8 \\ \frac{\partial f}{\partial y}=2 y$
अब द्विक बिन्दुओं के अस्तित्व के लिए
$\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0 \\ -3 x^2+10 x-8=0 \\ \Rightarrow 3 x^2-10 x+8=0 \\ \Rightarrow 3 x^2-6 x-4 x+8=0 \\ \Rightarrow 3 x\left[ (x-2)-4(x-2) \right]=0 \\ =(x-2)(3 x-4)=0$
तथा $2 y=0 \Rightarrow y=0 \\ \Rightarrow x=2, \frac{4}{3}$
अतः $(2,0),\left(\frac{4}{3}, 0\right)$ बिन्दु प्राप्त होते हैं।इनमें (2,0) वक्र पर विद्यमान है।फलतः (2,0) द्विक बिन्दु है।

$\frac{\partial^2 f}{\partial x^2}=-6 x+10, \frac{\partial^2 f}{\partial y^2}=2, \frac{\partial^2 f}{\partial x \partial y}=0 \\ \left(\frac{\partial^2 f}{\partial x^2}\right)_{(2,0)}=-6 \times 2+10=-12+10=-2 \\ \left(\frac{\partial^2 f}{\partial y^2}\right)_{(2,0)}=2,\left(\frac{\partial^2 f}{\partial x \partial y}\right)_{(2,0)}=0 \\ \left(\frac{\partial^2 f}{\partial x \partial y}\right)^2>\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right) \\ \Rightarrow 0^2>(-2)(2) \\ \Rightarrow 0 >-4$
अतः बिन्दु (2,0) पर नोड है।
उपर्युक्त उदाहरणों के द्वारा अवकलन गणित में द्विक बिन्दु (Double Points in Differential Calculus),द्विक बिन्दु (Singular Points or Double Points) को समझ सकते हैं।

3.अवकलन गणित में द्विक बिन्दु पर आधारित सवाल (Questions Based on Double Points in Differential Calculus):

Double Points in Differential Calculus

निम्नलिखित वक्रों पर द्विक बिन्दुओं को निर्धारित कीजिए एवं उनकी प्रकृति को भी निश्चित कीजिएः
(Determine the existence and examine the nature of the double points on the following curves):

(1.) $y^3+3 a x^2+x^3=0$
(2.) $2\left(x^3+y^3\right)-3\left(3 x^2+y^2\right)+12 x=4$
(3.) $x^3-y^2-7 x^2+4 y+15 x-13=0$
उत्तर (Answers):(1.)(0,0) पर प्रथम प्रकार का उभयाग्र (cusp)
(2.)(1,1) पर नोड (node)
(3.)(3,2) पर नोड
उपर्युक्त सवालों को हल करने पर अवकलन गणित में द्विक बिन्दु (Double Points in Differential Calculus),द्विक बिन्दु (Singular Points or Double Points) को ठीक से समझ सकते हैं।

Also Read This Article:-Asymptotes of Polar Curves

4.अवकलन गणित में द्विक बिन्दु (Frequently Asked Questions Related to Double Points in Differential Calculus),द्विक बिन्दु (Singular Points or Double Points) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.नोड की परिभाषा दीजिए। (Define Node):

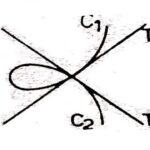
उत्तर:यदि वक्र पर बिन्दु P द्विक बिन्दु हो तथा बिन्दु पर वक्र की दोनों शाखाएँ वास्तविक हो तथा बिन्दु P पर संपाती स्पर्श रेखाएँ नहीं हों तो बिन्दु P को वक्र का नोड कहते हैं जैसा कि चित्र में दर्शाया गया है।

प्रश्न:2.उभयाग्र किसे कहते हैं और कितने प्रकार के होते हैं? (What is Called Cusp and How Many Types are There?):

उत्तर:यदि वक्र पर बिन्दु P द्विक बिन्दु हो तथा P पर वक्र की दोनों शाखाएँ वास्तविक हों तथा बिन्दु P पर संपाती स्पर्श रेखाएँ हों तो बिन्दु P को वक्र का उभयाग्र (cusp) कहते हैं जैसा कि चित्र में बताया गया है।
उभयाग्र के प्रकार (Kinds of Cusp):
(i)एकल उभयाग्र (Single Cusp):यदि वक्र की दो शाखाएँ उभयाग्र (cusp) पर उभयनिष्ठ अभिलम्ब (Common Normal) के एक ही ओर (same side) स्थित हों तो यह एकल उभयाग्र (single cusp) (देखो चित्र) कहलाता है।
(ii)द्विक उभयाग्र (Double cusp):यदि वक्र के उभयाग्र पर दोनों शाखाएँ उभयनिष्ठ अभिलम्ब के दोनों ओर अर्थात् विपरीत ओर (opposite side) स्थित हों तो वह द्विक उभयाग्र (Double cusp) (देखो चित्र) कहलाता है।

प्रश्न:3.उभयाग्र की जाति की परिभाषा दीजिए। (Define Species of Cusp):

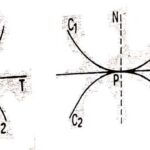
उत्तर:उभयाग्र की जाति (Species of Cusp):एक उभयाग्र (एकल अथवा द्विक) प्रथम अथवा द्वितीय जाति का उभयाग्र कहलाता है, यदि वक्र की शाखाएँ उभयनिष्ठ स्पर्श रेखा के विपरीत दिशा में स्थित हों अथवा एक ही दिशा में स्थित हो।

प्रश्न:4.वियुक्त बिन्दु किसे कहते हैं? (What is Conjugate Point?):

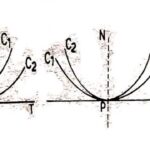
उत्तर:वियुक्त बिन्दु (Conjugate Point):यदि वक्र पर कोई बिन्दु इस प्रकार से हो कि जिससे निकट वक्र का कोई वास्तविक बिन्दु स्थित न हो तो ऐसे बिन्दु को एक विलगित (isolated) या वियुक्त (conjugate) बिन्दु कहते हैं।

प्रश्न:5.द्विक बिन्दु विद्यमान होने का आवश्यक प्रतिबन्ध लिखिए। (Write the Necessary Condition for the Existence of Double Points):

उत्तर:द्विक बिन्दु होने के लिए आवश्यक प्रतिबन्ध (Necessary Condition for the Existence of Double Points):
यदि वक्र का समीकरण f(x,y)=0 तथा P(x,y) इस पर कोई बिन्दु है तो बिन्दु P पर स्पर्श रेखा का झुकाव (slope) होगाः
$\frac{d y}{d x}=-\frac{\frac{\partial f }{\partial x}}{\frac{\partial f }{\partial y}} \\ \Rightarrow \frac{\partial f}{\partial x}+\frac{\partial f}{\partial y} \cdot \frac{d y}{d x}=0 \cdots(1)$
अब हम द्विक बिन्दु की परिभाषा से जानते हैं कि द्विक बिन्दु पर दो स्पर्श रेखाएँ होती है।यदि P एक द्विक बिन्दु है तो (1) से $\frac{d y}{d x}$ के मान प्राप्त होने चाहिए।परन्तु (1) एकघाती व्यंजक है,अतः यह के एक से अधिक मानों के लिए तभी सन्तुष्ट होगा जबकि $\frac{\partial f}{\partial x}=0$ तथा $\frac{\partial f}{\partial y}=0$ हो।
अतः वक्र f(x,y) के बिन्दु P(x,y) के द्विक बिन्दु होने के लिए प्रतिबन्ध निम्न हैः
$\frac{\partial f}{\partial x}=0 , \frac{\partial f}{\partial y}=0$ तथा f=0
अब द्विक बिन्दु पर
$\frac{d y}{d x}=-\frac{\frac{\partial f }{\partial x}}{\frac{\partial f }{\partial y}} \\ =-\frac{\frac{d}{d x}\left(\frac{\partial f}{\partial x}\right)}{\frac{d}{d x} \left(\frac{\partial f}{\partial y}\right)}$ [L-हाॅस्पीटल नियम से]
= $\frac{\left(\frac{\partial^2 f}{\partial x^2}\right)+\frac{\partial^2 f}{\partial x \partial y} \cdot \frac{d y}{d x}}{\frac{\partial f^{2}}{\partial x \partial y}+\frac{\partial^{2} f}{\partial x^2} \cdot \frac{d y}{d x}}$
सरल करने पर
$\frac{\partial^2 f}{\partial y^2}\left(\frac{d y}{d x}\right)^2+2 \frac{\partial^{2} f}{\partial x \partial y}\left(\frac{d y}{d x}\right)+\frac{\partial^2 f}{\partial x^{2}}=0 \cdots(2)$
अब यदि $\frac{\partial^2 f}{\partial x^2}, \frac{\partial^2 f}{\partial x \partial y}$ तथा $\frac{\partial^2 f}{\partial y^2}$ सब एक साथ शून्य न हों तो $\frac{d y}{d x}$ दो के मान ज्ञात कर सकते हैं जो कि वास्तविक एवं पृथक-पृथक,वास्तविक एवं सम्पाती या अधिकल्पित निम्न अनुसार होंगेः
$\left(\frac{\partial^2 f}{\partial x \partial y}\right)^{2}>=<\left(\frac{\partial^2 f}{\partial x^{2}}\right)\left(\frac{\partial^2 f}{\partial y^{2}}\right)$
अतः बिन्दु P नोड (Node), उभयाग्र (Cusp) या वियुक्त बिन्दु (Conjugate) निम्न अनुसार होगाः
$\left(\frac{\partial^2 f}{\partial x \partial y}\right)^{2}>=<\left(\frac{\partial^2 f}{\partial x^{2}}\right)\left(\frac{\partial^2 f}{\partial y^{2}}\right)$
उपर्युक्त प्रश्नों के उत्तर द्वारा अवकलन गणित में द्विक बिन्दु (Double Points in Differential Calculus),द्विक बिन्दु (Singular Points or Double Points) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Double Points in Differential Calculus

अवकलन गणित में द्विक बिन्दु
(Double Points in Differential Calculus)

Double Points in Differential Calculus

About Author

Satyam

About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.