Derivative of implicit functions
1.अस्पष्ट फलनों का अवकलज का परिचय (Introduction to Derivative of implicit functions)-
अस्पष्ट फलनों का अवकलज (Derivative of implicit functions) ज्ञात करने के लिए अवकलज का श्रृंखला नियम,अवकलज का गुणनफल नियम,अवकलज का भागफल नियम का प्रयोग करते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
(1.)परिचय (Introduction)-
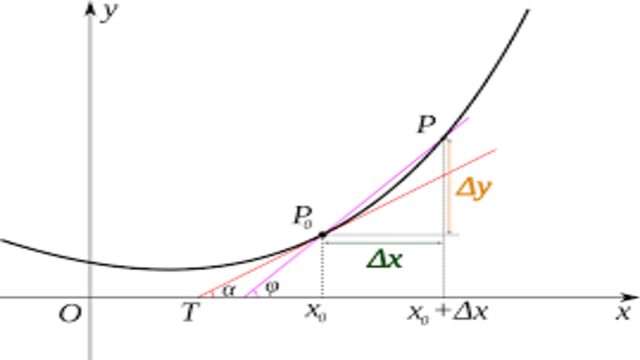
माना कि y=f(x)चर राशि x. का कोई संतत फलन है जहां x स्वतन्त्र तथा y आश्रित चर राशियां हैं। चूंकि y का मान x के मान पर आश्रित है, अतः x के मान में जब कोई परिवर्तन करते हैं तो y के मान में भी परिवर्तन होगा।
जब किसी चर राशि के एक मान से दूसरे निकटतम मान में परिवर्तन होता है तब इन दोनों मानों के अन्तर को ‘वृद्धि ‘ (Increment) कहते हैं। उदाहरणार्थ चर राशि x के दोनों मान x+\delta xऔर x के अन्तर को x में वृद्धि कहते हैं।इस वृद्धि \delta xको से व्यक्त करते हैं।
चूंकि y का मान x के मान पर आश्रित है अतः x के मान में कोई स्वेच्छ (arbitrary) अल्प वृद्धि \delta xकी जाय तो y के मान में भी संगत वृद्धि \delta yहोगी तो भिन्न\frac { \delta y }{ \delta x } के सापेक्ष,y की वृद्धि की औसत दर होगी और यदि\delta x छोटा होता शून्य की ओर अग्रसर हो,तो \delta yभी छोटा होता हुआ शून्य की ओर अग्रसर होगा।
(2.)अवकलज (Derivative)-
माना कि y=f(x) कोई संतत फलन है। माना x में अल्प वृद्धि \delta xकी जाए तो y के मान में संगत वृद्धि \delta yहोगी तो भिन्न \frac { \delta y }{ \delta x } की सीमा जब \delta x\rightarrow 0 अर्थात् \lim _{ sx\rightarrow 0 }{ \frac { \delta y }{ \delta x } } (यदि विद्यमान हो) को y का x के सापेक्ष अवकलज या अवकल गुणांक (Differential Co-efficient) कहते हैं।इसे\frac { dy }{ dx } से व्यक्त करते हैं।
अर्थात् यदिy=f\left( x \right)
तो y+\delta y=f\left( x+\delta x \right) \\ \delta y=f\left( x+\delta x \right) -f\left( x \right) \\ \frac { \delta y }{ \delta x } =\frac { f\left( x+\delta x \right) -f\left( x \right) }{ \delta x } \\ \frac { dy }{ dx } =\lim _{ sx\rightarrow 0 }{ \frac { \delta y }{ \delta x } } \\ \frac { dy }{ dx } =\lim _{ sx\rightarrow 0 }{ \frac { f\left( x+\delta x \right) -f\left( x \right) }{ \delta x } }
Also Read This Article:-Trigonometrical Ratios of Compound Angles
2.अस्पष्ट फलनों का अवकलज (Derivative of implicit functions)-
(1.) कोई फलन जो f\left( { x }_{ 1 },{ x }_{ 2 },{ x }_{ 3 },.........{ x }_{ n },y \right) =0जैसे किसी समीकरण द्वारा निर्धारित हो। यहां यदि y को आश्रित चर माना जाय तो उसे इस समीकरण द्वारा निर्धारित अस्पष्ट फलन कहते हैं, जहां { x }_{ 1 },{ x }_{ 2 },{ x }_{ 3 },.........{ x }_{ n } स्वतन्त्र चर है। उदाहरणार्थ{ y }^{ 3 }+3{ x }^{ 2 }y+x+9=0 में y को x का अस्पष्ट फलन कहते हैं।
(2.)जब किसी समीकरण में x तथा y दोनों चर हों तथा इसमें y को x के ( या x को y के ) फलन के रूप में स्पष्ट पदों में व्यक्त किया जा सके तब y को x के ( या x को y के) स्पष्ट फलन( Explicit Function) कहते हैं। उपर्युक्त में यदि y को x के (या x को y के) फलन के रूप में स्पष्ट पदों में व्यक्त नहीं किया जा सके तो ऐसे फलनों को अस्पष्ट फलन (Implicit function) कहते हैं।
3.अस्पष्ट फलनों का अवकलज के उदाहरण (Examples of Derivative of implicit functions)-
निम्नलिखित फलनों से\frac { dy }{ dx } ज्ञात कीजिए-
Question-1.{ x }^{ 3 }+{ y }^{ 3 }=3axy
Solution-{ x }^{ 3 }+{ y }^{ 3 }=3axy
अवकलन करने पर
{ x }^{ 3 }+{ y }^{ 3 }=3axy\\ { 3x }^{ 2 }+{ 3y }^{ 2 }\frac { dy }{ dx } =3ay+3ax\frac { dy }{ dx } \\ { 3y }^{ 2 }\frac { dy }{ dx } -3ax\frac { dy }{ dx } =3ay-{ 3x }^{ 2 }\\ \frac { dy }{ dx } \left( { y }^{ 2 }-ax \right) =ay-{ x }^{ 2 }\\ \frac { dy }{ dx } =\frac { ay-{ x }^{ 2 } }{ { y }^{ 2 }-ax }
Question-2.sin\left( xy \right) +\frac { x }{ y } ={ x }^{ 2 }-y
Solution-cos\left( xy \right) \left[ y+x\frac { dy }{ dx } \right] +\frac { y.1-x\frac { dy }{ dx } }{ { y }^{ 2 } } =2x-\frac { dy }{ dx } \\ y\quad cos\left( xy \right) +x\quad cos\left( xy \right) \frac { dy }{ dx } +\frac { 1 }{ y } -\frac { x }{ { y }^{ 2 } } \frac { dy }{ dx } =2x-\frac { dy }{ dx } \\ x\quad cos\left( xy \right) \frac { dy }{ dx } -\frac { x }{ { y }^{ 2 } } \frac { dy }{ dx } +\frac { dy }{ dx } =2x-y\quad cos\left( xy \right) -\frac { 1 }{ y } \\ \frac { dy }{ dx } \left[ x\quad cos\left( xy \right) -\frac { x }{ { y }^{ 2 } } +1 \right] =\frac { 2xy-{ y }^{ 2 }\quad cos\left( xy \right) -1 }{ y } \\ \frac { dy }{ dx } \left[ \frac { x{ y }^{ 2 }\quad cos\left( xy \right) -x+{ y }^{ 2 } }{ { y }^{ 2 } } \right] =\frac { 2xy-{ y }^{ 2 }\quad cos\left( xy \right) -1 }{ y } \\ \frac { dy }{ dx } =\frac { y\left[ 2xy-{ y }^{ 2 }\quad cos\left( xy \right) -1 \right] }{ x{ y }^{ 2 }\quad cos\left( xy \right) -x+{ y }^{ 2 } }
इस प्रकार अस्पष्ट फलनों के अवकलज ( Derivative of implicit functions) के उदाहरणों से हम अस्पष्ट फलनों का अवकलज( Derivative of implicit functions) को ठीक से समझ सकते हैं।
Question-3.{ x }^{ y }+{ y }^{ x }={ a }^{ b }
Solution-माना u={ x }^{ y },v={ y }^{ x }\\ \log { u } =y\log { x } ,\quad \log { v } =x\log { y } \\ \frac { 1 }{ u } \frac { du }{ dx } =\frac { y }{ x } +\log { x } \frac { dy }{ dx } \quad ,\quad \frac { 1 }{ v } \frac { dv }{ dx } =\log { y } +\frac { x }{ y } \frac { dy }{ dx } \\ \frac { du }{ dx } =u\left[ \frac { y }{ x } +\log { x } \frac { dy }{ dx } \right] ,\quad \quad \quad \frac { dv }{ dx } =v\left[ \log { y } +\frac { x }{ y } \frac { dy }{ dx } \right] \\ u+v={ a }^{ b }\\ \frac { du }{ dx } +\frac { dv }{ dx } =0\\ u\left[ \frac { y }{ x } +\log { x } \frac { dy }{ dx } \right] +v\left[ \log { y } +\frac { x }{ y } \frac { dy }{ dx } \right] =0\\ { x }^{ y }\left[ \frac { y }{ x } +\log { x } \frac { dy }{ dx } \right] +{ y }^{ x }\left[ \log { y } +\frac { x }{ y } \frac { dy }{ dx } \right] =0\\ { x }^{ y-1 }y+{ x }^{ y }\log { x } \frac { dy }{ dx } +{ y }^{ x }\log { y } +{ y }^{ x-1 }x\frac { dy }{ dx } =0\\ { x }^{ y }\log { x } \frac { dy }{ dx } +{ y }^{ x-1 }x\frac { dy }{ dx } =-\left[ { x }^{ y-1 }y+{ y }^{ x }\log { y } \right] \\ \frac { dy }{ dx } \left[ { x }^{ y }\log { x } +{ y }^{ x-1 }x \right] =-\left[ { x }^{ y-1 }y+{ y }^{ x }\log { y } \right] \\ \frac { dy }{ dx } =\frac { -\left[ { x }^{ y-1 }y+{ y }^{ x }\log { y } \right] }{ \left[ { x }^{ y }\log { x } +{ y }^{ x-1 }x \right] }
Also Read This Article:-Integration by use of standard formula
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |