Definite Integral as limit of sum
1.योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum)-
- योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) को समझने के लिए हमे निश्चिंत समाकल को समझना आवश्यक है।समाकल में निश्चित और अनिश्चित समाकल के पदों का प्रयोग किया जाता है। अंग्रेजी में निश्चित समाकल के लिए Definite Integral तथा अनिश्चित समाकल के लिए Indefinite Integral का प्रयोग किया जाता है।
(1.)समाकल (Integral )-
- समाकलन को अवकलन की विपरीत प्रक्रिया के रूप में जाना जाता है। परन्तु समाकलन गणित की खोज अवकलन गणित से पूर्व हुई थी।समाकलन गणित का प्रयोग समतल क्षेत्रों के क्षेत्रफल ज्ञात करने के लिए ऐसी अनन्त श्रेणी के योग के रूप में हुई जिसका प्रत्येक पद शून्य की और अग्रसर था।बाद में समतलीय वक्रों के क्षेत्रफल, ठोसों का आयतन,गुरुत्व केन्द्र इत्यादि ज्ञात करने हेतु व्यापक विधियों की आवश्यकता के फलस्वरूप इसका विकास हुआ।
(2.)समाकलन और अवकलन गणित में अन्तर (Differerence between Integral calculus and Differential Calculus)-
- अवकलन गणित में हम दिए हुए फलनों के अवकल गुणांक ज्ञात करते हैं जबकि समाकलन गणित में हम वह फलन ज्ञात करते हैं जिसका अवकल गुणांक दिया हुआ होता है।समाकलन अवकलन की प्रतिलोम (Inverse) प्रक्रिया है तथा इसे प्रतिअवकलज (Antiderivative ) या पूर्वग (primitive) भी कहते हैं।
(3.)अनिश्चित समाकल (Indefinite Integral)-
- वह फलन जिसका अवकलज दिया हुआ फलन हो,वह समाकल जिसकी सीमाएं न दी हुई हो जैसे \int { { x }^{ 2 }dx } ,\int { sinxdx } इत्यादि।अनिश्चित समाकल की पहचान यह है कि समाकलन करने के बाद अन्त में अचरांक का प्रयोग करते हैं।
किसी भी फलन का विभिन्न तरीकों अथवा विधियों से समाकलन करने पर हमेशा उनमें एक अचर का ही अन्तर होता है।
इसलिए अनिश्चित समाकलन करने के बाद हमेशा एक अचर अवश्य जोड़ना चाहिए।
समाकलन का अचरांक,चर राशि से स्वतन्त्र होता है।अचरांक के भिन्न-भिन्न मान लेने पर फलन के भिन्न-भिन्न समाकल प्राप्त होते हैं जिनमें केवल अचर पद का ही अन्तर होता है।
(4.)निश्चित समाकल (Definite Integral)-
- वह समाकल जिसकी ऊपरी तथा निम्न दोनों सीमाएं दी हुई हो जैसे-\int _{ 0 }^{ \frac { \pi }{ 4 } }{ tanxdx }
- सीमाओं का ध्यान रखे बिना समाकल निकालने के पश्चात् जो परिणाम प्राप्त होता हैं उसमें चर के स्थान पर ऊपरी सीमा तथा निम्न सीमा का मान रखने पर हमें दो मान प्राप्त होते हैं।पहले परिणाम में से दूसरे परिणाम को घटाकर निश्चित समाकल का मान प्राप्त करते हैं।
- निश्चित समाकल का मान या तो श्रेणी के योगफल की सीमा के रूप में ज्ञात किया जाता है अथवा अन्तराल [a,b] में इसका समाकल (प्रतिअवकलज) F होने पर अंतिम बिन्दुओं पर F के मानों के अन्तर F(b)-F(a) के बराबर होता है।
इस आर्टिकल में योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) का अध्ययन करेंगे। - आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Integration by use of standard formula
2.योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum)-
यदि किसी श्रेणी में पदो की संख्या अनन्त की ओर व प्रत्येक पद शून्य की ओर अग्रसर हो तो निश्चित समाकल एक श्रेणी के योगफल की सीमा के रूप में परिभाषित किया जाता है।
परिभाषा (Definition)-
यदि अन्तराल [a,b] में परिभाषित कोई वास्तविक मानों का सतत फलन f(x) और अन्तराल [a,b] को n बराबर भागों में बिन्दुओं a+h,a+2h,a+3h,………,a+(n-1)h द्वारा (जहां h प्रत्येक भाग की लम्बाई है) विभाजित किया जाता तो
\int _{ a }^{ b }{ f\left( x \right) dx } =_{ h\rightarrow 0 }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) + \\ f\left( a+2h \right) +......... \\ .......+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }
(जहां n\rightarrow \infty तथा nh=b-a)
इस परिभाषा के प्रयोग से निश्चित समाकल के मान ज्ञात करने की विधि को प्रथम सिद्धान्त (ab-initio method) से समाकलन ज्ञात करना कहते हैं।यह व्यंजक योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) की परिभाषा कहलाता है।
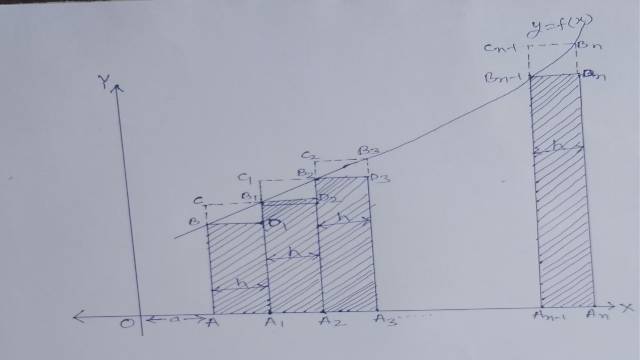
उपपत्ति (Proof)-माना f(x) चित्रानुसार अन्तराल [a,b] को h ऊंचाई के n अन्तरालों में विभाजित करने पर
A{ A }_{ n }=O{ A }_{ n }-O{ A }_{ 1 }\\ \Rightarrow A{ A }_{ 1 }+{ A }_{ 1 }{ A }_{ 2 }+{ A }_{ 2 }{ A }_{ 3 }+.......+{ A }_{ n-1 }{ A }_{ n }=b-a\\ \Rightarrow h+h+h+.........+h\quad (n\quad बार )=b-a\\ \Rightarrow nh=b-a\\ \Rightarrow h=\frac { b-a }{ n }
माना y=f(x) जब x=a,y=f(a)
अतः B के निर्देशांक (a,f(a)) होंगे।
अर्थात् AB=f(a)
इसी प्रकार
{ A }_{ 1 }{ B }_{ 1 }=f\left( a+h \right) ,{ A }_{ 2 }{ B }_{ 2 }=f\left( a+2h \right) ,......,{ A }_{ n }{ B }_{ n }=f\left( a+nh \right)
चित्रानुसार छायांकित आयताकार पट्टिकाओं,जो कि वक्र के नीचे है,के योगफलों का योगफल{ \triangle }_{ 1 } हो तो
[katex]{ \triangle }_{ 1 }=आयतA{ A }_{ 1 }{ D }_{ 1 }B+आयत{ A }_{ 1 }{ A }_{ 2 }{ D }_{ 2 }{ B }_{ 1 }+……..+आयत{ A }_{ n-1 }{ A }_{ n }{ D }_{ n }{ B }_{ n-1 }\\ =AB\times A{ A }_{ 1 }+{ A }_{ 1 }{ B }_{ 1 }\times { A }_{ 1 }{ A }_{ 2 }+………+{ A }_{ n-1 }{ B }_{ n-1 }\times { A }_{ n-1 }{ A }_{ n }\\ =f\left( a \right) \times h+f\left( a+h \right) \times h+f\left( a+2h \right) \times h+………….+f\left( a+\overline { n-1 } h \right) \times h\\ =h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) +f\left( a+2h \right) \\ +………….+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] [/katex]
वक्र y=f(x),x-अक्ष तथा दो कोटियों x=a,x=b से परिबद्ध क्षेत्रफल A{ A }_{ n }{ B }_{ n }BA को \triangle से प्रकट करें तो { \triangle }_{ 1 } का मान से कम \triangle होगा। पुनः माना
{ \triangle }_{ 2 }=आयतA{ A }_{ 1 }{ B }_{ 1 }C+आयत{ A }_{ 1 }{ A }_{ 2 }{ B }_{ 2 }{ C }_{ 1 }+........+आयत{ A }_{ n-1 }{ A }_{ n }{ B }_{ n }{ C }_{ n-1 }\\ ={ A }_{ 1 }{ B }\times A{ A }_{ 1 }+{ A }_{ 2 }{ B }_{ 2 }\times { A }_{ 1 }{ A }_{ 2 }+.........+{ A }_{ n }{ B }_{ n }\times { A }_{ n-1 }{ A }_{ n }\\ =f\left( a+h \right) \times h+f\left( a+2h \right) \times h+.............+f\left( a+nh \right) \times h\\ =h\left[ \begin{matrix} f\left( a+h \right) +f\left( a+2h \right) + \\ .............+f\left( a+nh \right) \end{matrix} \right]
यह क्षेत्रफल \triangle से अधिक होगा,इस प्रकार \triangle का मान { \triangle }_{ 1 } से अधिक व { \triangle }_{ 2 } से कम होगा अर्थात्
{ \triangle }_{ 1 }<\triangle <{ \triangle }_{ 2 }
पुनः{ \triangle }_{ 2 }-\triangle =hf\left( a+nh \right) -hf\left( a \right) \\ =h\left[ f\left( b \right) -f\left( a \right) \right] \quad \left[ \because a+nh=b \right]
स्पष्टत: जब आयताकार पट्टिकाओं की चौड़ाई h अत्यल्प होगी अर्थात् h\rightarrow 0 तो { \triangle }_{ 1 } और { \triangle }_{ 2 } का मान \triangle के अत्यधिक निकट होगा।
अर्थात् _{ h\rightarrow 0 }^{ lim }{ { \triangle }_{ 1 } }=_{ h\rightarrow 0 }^{ lim }{ { \triangle }_{ 2 } }=\triangle
अतः \triangle =\int _{ a }^{ h }{ f\left( x \right) dx } \\ =_{ h\rightarrow 0 }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) +f\left( a+2h \right) \\ +.....+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }
एवं \triangle =\int _{ a }^{ b }{ f\left( x \right) dx } \\ =_{ h\rightarrow 0 }^{ lim }h\left[ \begin{matrix} f\left( a+h \right) +f\left( a+2h \right) + \\ .............+f\left( a+nh \right) \end{matrix} \right]
उपर्युक्त योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) के रूप में निम्न प्रकार लिख सकते है-
(i)\int _{ a }^{ b }{ f\left( x \right) dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) +f\left( a+2h \right) + \\ .............+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }
[जहां h=\frac { b-a }{ n } स्पष्टत: n\rightarrow \infty तो h\rightarrow 0]
(ii)\int _{ a }^{ b }{ f\left( x \right) dx } \\ =_{ n\rightarrow \infty }^{ lim }h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) +f\left( a+2h \right) + \\ ............+f\left( a+nh \right) \end{matrix} \right]
[जहां h=\frac { b-a }{ n } ]
कुछ महत्त्वपूर्ण परिणाम (Some important results)-
(i){ \sum { r } =1+2+3+.......+n=\frac { n\left( n+1 \right) }{ 2 } }
(ii){ \sum { r } }=1+2+3+.......+n=\frac { n\left( n+1 \right) }{ 2 }
(iii)\sum { { r }^{ 3 } } ={ 1 }^{ 3 }+{ 2 }^{ 3 }+{ 3 }^{ 3 }+........+{ n }^{ 3 }={ \left[ \frac { n\left( n+1 \right) }{ 2 } \right] }^{ 2 }
(iv)\sum { \left( 2r-1 \right) } =1+3+5+.....+\left( 2n-1 \right) ={ n }^{ 2 }
(v)a+\left( a+d \right) +\left( a+2d \right) +.....+a+\overline { n-1 } d=\frac { n }{ 2 } \left[ 2a+\left( n-1 \right) d \right]
(vi)a+ar+a{ r }^{ 2 }+........+a{ r }^{ n-1 }=\frac { a\left( { r }^{ n }-1 \right) }{ \left( r-1 \right) } ;r\neq 1
3.योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) पर आधारित सवाल-
योगफल की सीमा के रूप में निश्चित समाकलों (Definite Integral as limit of sum) के प्रथम सिद्धान्त से मान ज्ञात करो
Question-1.\int _{ a }^{ b }{ { x }^{ 2 }dx }
Solution-\int _{ a }^{ b }{ { x }^{ 2 }dx } \\ f\left( x \right) ={ x }^{ 2 }\quad ,h=\frac { b-a }{ n } \quad \Rightarrow nh=b-a
योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) का सूत्र-
\int _{ a }^{ b }{ f\left( x \right) dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) \\ +f\left( a+2h \right) +.... \\ ..+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }\\ \Rightarrow \int _{ a }^{ b }{ { x }^{ 2 }dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) \\ +f\left( a+2h \right) +.... \\ ..+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }.......(1)
f\left( x \right) ={ x }^{ 2 }\\ f\left( a \right) ={ a }^{ 2 },f\left( a+h \right) ={ \left( a+h \right) }^{ 2 },f\left( a+2h \right) ={ \left( a+2h \right) }^{ 2 }\\ f\left( a+\overline { n-1 } h \right) ={ \left[ a+\overline { n-1 } h \right] }^{ 2 }
उपर्युक्त मान समीकरण (1) में रखने पर-
\int _{ a }^{ b }{ { x }^{ 2 }dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} { a }^{ 2 }+{ \left( a+h \right) }^{ 2 } \\ +{ \left( a+2h \right) }^{ 2 }+.. \\ ...+{ \left( a+\overline { n-1 } h \right) }^{ 2 } \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} { a }^{ 2 }+{ a }^{ 2 }+2ah+{ h }^{ 2 }+{ a }^{ 2 } \\ +4ah+{ 4h }^{ 2 }+.......+{ a }^{ 2 } \\ +2a\left( n-1 \right) h+{ \left( n-1 \right) }^{ 2 }{ h }^{ 2 } \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} { a }^{ 2 }+{ a }^{ 2 }+{ a }^{ 2 }+........n+ \\ 2ah+4ah+...+2a\left( n-1 \right) h \\ { +h }^{ 2 }+{ 4h }^{ 2 }{ +....+\left( n-1 \right) }^{ 2 }{ h }^{ 2 } \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} { na }^{ 2 }+ \\ 2ah\left( 1+2+......+\left( n-1 \right) \right) + \\ { h }^{ 2 }\left( { 1 }^{ 2 }+{ 2 }^{ 2 }+..+{ \left( n-1 \right) }^{ 2 } \right) \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} { na }^{ 2 }+2ah\frac { n\left( n-1 \right) }{ 2 } + \\ { h }^{ 2 }\frac { n\left( n-1 \right) \left( 2n-1 \right) }{ 6 } \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ nh\left[ \begin{matrix} { a }^{ 2 }+anh\left( 1-\frac { 1 }{ n } \right) + \\ \frac { { n }^{ 2 }{ h }^{ 2 } }{ 6 } \left( 1-\frac { 1 }{ n } \right) \left( 2-\frac { 1 }{ n } \right) \end{matrix} \right] }\\ =\left( b-a \right) { \left[ { \begin{matrix} { a }^{ 2 }+a\left( b-a \right) \left( 1-0 \right) \\ +\frac { { \left( b-a \right) }^{ 2 } }{ 6 } \left( 1-0 \right) \left( 2-0 \right) \end{matrix} } \right] }\\ =\left( b-a \right) { \left[ { a }^{ 2 }+a\left( b-a \right) +\frac { { \left( b-a \right) }^{ 2 } }{ 3 } \right] }\\ =\frac { \left( b-a \right) \left[ 3{ a }^{ 2 }+3ab-{ 3a }^{ 2 }+{ b }^{ 2 }{ +a }^{ 2 }-2ab \right] }{ 3 } \\ =\frac { 1 }{ 3 } \left( b-a \right) \left[ { a }^{ 2 }+{ b }^{ 2 }+ab \right] \\ =\frac { 1 }{ 3 } \left( { b }^{ 3 }{ - }{ a }^{ 3 } \right)
Question-2.\int _{ a }^{ b }{ { e }^{ -x }dx }
Solution-\int _{ a }^{ b }{ { e }^{ -x }dx } \\ f\left( x \right) ={ e }^{ -x }dx,h=\frac { b-a }{ n } \Rightarrow nh=b-a
योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) का सूत्र-
\int _{ a }^{ b }{ f\left( x \right) dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) \\ +f\left( a+2h \right) +.... \\ ..+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }\\ \int _{ a }^{ b }{ { e }^{ -x }dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) \\ +f\left( a+2h \right) +.... \\ ..+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }.......(1)
f\left( x \right) ={ e }^{ -x }\\ f\left( a \right) ={ e }^{ -a },f\left( a+h \right) ={ { e }^{ -\left( a+h \right) } },f\left( a+2h \right) ={ e }^{ -\left( a+2h \right) }\\ f\left( a+\overline { n-1 } h \right) ={ e }^{ -\left[ a+\left( n-1 \right) h \right] }
उपर्युक्त मान समीकरण (1) में रखने पर-
\int _{ a }^{ b }{ { e }^{ -x }dx } =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} { e }^{ -a }+{ { e }^{ -\left( a+h \right) } }+{ e }^{ -\left( a+2h \right) }+ \\ ...........+{ e }^{ -\left[ a+\left( n-1 \right) h \right] } \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ { \begin{matrix} { e }^{ -a }(1+{ { e }^{ -h } }+{ e }^{ -2h }+.... \\ +{ e }^{ -\left( n-1 \right) h }) \end{matrix} } \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ { e }^{ -a }\left( \frac { { e }^{ -nh }-1 }{ { e }^{ -h }-1 } \right) \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ { e }^{ -a }\left( \frac { { e }^{ -nh }-1 }{ -h } .\frac { -h }{ { e }^{ -h }-1 } \right) \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ nh\left[ { e }^{ -a }\left( n\frac { { e }^{ -nh }-1 }{ -nh } .\frac { -h }{ { e }^{ -h }-1 } \right) \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ nh\left[ { e }^{ -a }\left( \frac { { e }^{ -nh }-1 }{ -nh } .\frac { -h }{ { e }^{ -h }-1 } \right) \right] }\\ ={ \left( b-a \right) \left[ { e }^{ -a }\left( \frac { { e }^{ -\left( b-a \right) }-1 }{ -\left( b-a \right) } .1 \right) \right] }\\ ={ \left[ { -e }^{ -a }\left( { e }^{ -\left( b-a \right) }-1 \right) \right] }\\ ={ \left[ { -e }^{ -a }\left( { e }^{ \left( a-b \right) }-1 \right) \right] }\\ ={ -e }^{ -b }+{ e }^{ -a }\\ ={ e }^{ -a }{ -e }^{ -b }
Question-3.\int _{ 1 }^{ 3 }{ \left( 2{ x }^{ 2 }+5 \right) dx }
Solution-\int _{ 1 }^{ 3 }{ \left( 2{ x }^{ 2 }+5 \right) dx } \\ f\left( x \right) =2{ x }^{ 2 }+5,\\ h=\frac { b-a }{ n } \Rightarrow nh=b-a\\ \Rightarrow nh=3-1\\ \Rightarrow nh=2
योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) का सूत्र-
\int _{ a }^{ b }{ f\left( x \right) dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( a \right) +f\left( a+h \right) \\ +f\left( a+2h \right) +.... \\ ..+f\left( a+\overline { n-1 } h \right) \end{matrix} \right] }\\ \int _{ 1 }^{ 3 }{ \left( 2{ x }^{ 2 }+5 \right) dx } \\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} f\left( 1 \right) +f\left( 1+h \right) \\ +f\left( 1+2h \right) +.... \\ ..+f\left( 1+\overline { n-1 } h \right) \end{matrix} \right] }......(1)
f\left( x \right) =2{ x }^{ 2 }+5\\ f\left( 1 \right) =2{ \left( 1 \right) }^{ 2 }+5=2+5\\ ,f\left( 1+h \right) =2{ \left( 1+h \right) }^{ 2 }+5,f\left( 1+2h \right) =2{ \left( 1+2h \right) }^{ 2 }+5\\ f\left( 1+\overline { n-1 } h \right) =2{ \left( 1+\overline { n-1 } h \right) }^{ 2 }+5
उपर्युक्त मान समीकरण (1) में रखने पर-
=_{ n\rightarrow \infty }^{ lim }{ h }\\ \left[ \begin{matrix} 2+5+2\left( 1+2h+{ h }^{ 2 } \right) +5+ \\ 2\left( 1+4h+{ 4h }^{ 2 } \right) +5+...+2 \\ \left( 1+2\left( n-1 \right) h+{ { \left( n-1 \right) }^{ 2 }h }^{ 2 } \right) +5 \end{matrix} \right] \\ =_{ n\rightarrow \infty }^{ lim }{ { h\left[ \begin{matrix} 7+2+4h+2{ h }^{ 2 }+5+2+8h \\ +{ 8h }^{ 2 }+5+.....+2+ \\ 4\left( n-1 \right) h+2{ { \left( n-1 \right) }^{ 2 }h }^{ 2 }+5 \end{matrix} \right] } }\\ =_{ n\rightarrow \infty }^{ lim }{ { h\left[ \begin{matrix} 7+7+7+7+7.....+n+ \\ 4h+8h+....+4\left( n-1 \right) h+ \\ 2{ h }^{ 2 }+{ 8h }^{ 2 }+...+2{ { \left( n-1 \right) }^{ 2 }h }^{ 2 } \end{matrix} \right] } }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} 7n+ \\ 4h\left( 1+2+3....+\left( n-1 \right) \right) + \\ { 2h }^{ 2 }\left( { 1 }^{ 2 }+{ 2 }^{ 2 }+....+{ \left( n-1 \right) }^{ 2 } \right) \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }{ h\left[ \begin{matrix} 7n+4h\frac { n\left( n-1 \right) }{ 2 } + \\ { 2h }^{ 2 }\frac { n\left( n-1 \right) \left( 2n-1 \right) }{ 6 } \end{matrix} \right] }\\ =_{ n\rightarrow \infty }^{ lim }\\ { nh\left[ \begin{matrix} 7+2nh\left( 1-\frac { 1 }{ n } \right) +</span> <span style="font-size: 14pt;">\\ \frac { { n }^{ 2 }{ h }^{ 2 } }{ 3 } \left( 1-\frac { 1 }{ n } \right) \left( 2-\frac { 1 }{ n } \right) \end{matrix} \right] }\\ =\left( 2 \right) { \left[ \begin{matrix} 7+2\left( 2 \right) \left( 1-0 \right) \\ +\frac { { \left( 2 \right) }^{ 2 } }{ 3 } \left( 1-0 \right) \left( 2-0 \right) \end{matrix} \right] }\\ =2\left[ 7+4+\frac { 4 }{ 3 } \left( 2 \right) \right] \\ =2\left[ 11+\frac { 8 }{ 3 } \right] \\ =2\left( \frac { 33+8 }{ 3 } \right) \\ =2\times \frac { 41 }{ 3 } \\ =\frac { 82 }{ 3 } \\ =27\frac { 1 }{ 3 }
उपर्युक्त सवालों के हल द्वारा योगफल की सीमा के रूप में निश्चित समाकल (Definite Integral as limit of sum) को समझा जा सकता है।
Also Read This Article:-Integration by Parts in Mathematics
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |