1.त्रिभुजों की समरूपता के लिए कसौटियाँ (Criteria for Similarity of Triangles),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10):

त्रिभुजों की समरूपता के लिए कसौटियाँ (Criteria for Similarity of Triangles) अर्थात् दो त्रिभुज समरूप होते हैं यदि उनके संगत कोण बराबर हों अथवा उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती हों) अथवा भुजा-कोण-भुजा समरूपता इत्यादि।
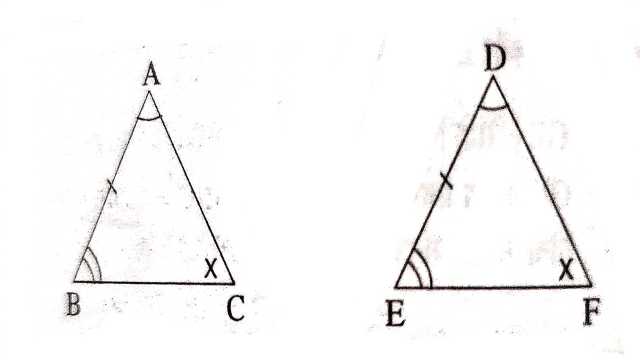
प्रमेय (Theorem):6.3.यदि दो त्रिभुजों में संगत कोण बराबर हों तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसलिए ये त्रिभुज समरूप होते हैं।
दिया है (Given):\triangle ABC \text { तथा } \triangle DEF समान कोणिक हैं अर्थात् \angle A=\angle D, \angle B=\angle E \text { तथा } \angle C=\angle F
सिद्ध करना है (To Prove): \triangle ABC \sim \triangle DEF
उपपत्ति (Proof): \triangle ABC की भुजा AB एवं \triangle DEF की भुजा DE में निम्न तीन स्थितियाँ हैंः
(i)AB=DE (ii)AB<DE (iii)AB>DE
प्रथम स्थिति (Case I):(i)जब AB=DE हो तो

\triangle ABC तथा \triangle DEF में
\angle A=\angle D (दिया है)
\angle B=\angle E (दिया है)
AB=DE (माना)
कोण-भुजा-कोण सर्वांगसमता से

\triangle ABC \cong \triangle DEF
अतः BC=EF, AC=DF, AB=DE

\Rightarrow \frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F} \\ \triangle ABC \sim \triangle DEF
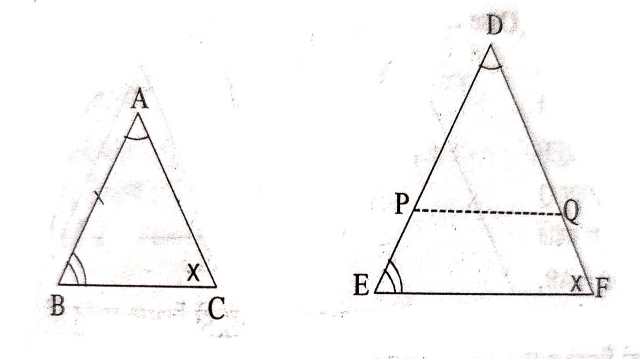
द्वितीय स्थिति (Case II):(ii).जब AB<DE हो
इस स्थिति में हम की भुजाओं DE तथा EF को क्रमशः P तथा Q तक इस प्रकार बढ़ाते हैं कि DP=AB,DQ=AC तथा PQ को मिलाते हैं।

उपपत्ति (Proof): \triangle ABC \text { और } \triangle DPQ में
AB=DP (रचना से)
AC=DQ (रचना से)
\angle A=\angle D(दिया है)
भुजा-कोण-भुजा सर्वांगसमता से
\triangle ABC \cong \triangle DPQ \\ \angle ABC=\angle DPQ \cdots(1) (CPCT से)
तथा \angle ACB=\angle DQP \cdots(2)
\angle ABC=\angle DEF (दिया है)…..(3)
\angle ACB=\angle DQP (दिया है)….(4)
(1),(2),(3) तथा (4) सेः

\angle DPQ=\angle DEF (संगत कोण)…..(5)
तथा \angle DQP=\angle DFE (संगत कोण)…..(6)
संगत कोण बराबर हैं अतः

PQ \| EF
(आधारभूत आनुपातिकता प्रमेय से)

\frac{D P}{D E}=\frac{D Q}{D F} \\ \Rightarrow \frac{A B}{D E}=\frac{A C}{D F} \cdots(7)
[DP=AB तथा DQ=AC ](रचना से)
इसी प्रकार हम सिद्ध कर सकते हैं कि

\frac{A B}{D E}=\frac{B C}{E F} \cdots(8)
(7) तथा (8) सेः

\Rightarrow \frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F} \\ \therefore \triangle ABC \sim \triangle DEF

द्वितीय स्थिति (Case III):(iii).जब AB>DE हो

इस स्थिति में हम \triangle DEF की भुजाओं DE तथा EF को क्रमशः P तथा Q तक इस प्रकार बढ़ाते हैं कि DP=AB,DQ=AC तथा PQ को मिलाते हैं।
उपपत्ति (Proof): \triangle ABC \text { और } \triangle DPQ में
AB=DP (रचना से)
AC=DQ (रचना से)
\angle A=\angle D(दिया है)
भुजा-कोण-भुजा सर्वांगसमता से
\triangle ABC \cong \triangle DPQ
\angle ABC=\angle DPQ (CPCT से)…..(1)
\angle ABC=\angle DEF (दिया है)…….(2)
(1) तथा (2) सेः

\angle DPQ=\angle DEF (संगत कोण)…..(3)
संगत कोण बराबर हैं अतः

PQ \| EF \\ \Rightarrow \frac{DE}{D P}=\frac{D F}{D Q}
(आधारभूत आनुपातिकता प्रमेय से)

[DP=AB तथा DQ=AC ](रचना से)
\Rightarrow\frac{D E}{A B}=\frac{D F}{A C} \\ \Rightarrow \frac{A B}{D E}=\frac{A C}{D F} \cdots(4)
इसी प्रकार हम सिद्ध कर सकते हैं कि

\frac{A B}{D E}=\frac{B C}{E F} \cdots(5)
(4) तथा (5) सेः

\frac{A B}{D E}=\frac{B C}{E F}=\frac{A E}{D F}
संगत भुजाएँ समानुपाती हैं

\Rightarrow \triangle ABC \sim \triangle DEF
उपप्रमेय (Corollary):कोण-कोण समरूपता गुणधर्म
यदि एक त्रिभुज के दो कोण दूसरे त्रिभुज के संगत दो कोणों के समान हों तो त्रिभुज समरूप होते हैं।
दिया है (Given):माना कि दो त्रिभुज \triangle ABC \text { व } \triangle DEF इस प्रकार हैं कि \angle A=\angle D \text { तथा } \angle B=\angle E
सिद्ध करना है (To Prove): \angle C=\angle F
उपपत्ति (Proof): \triangle ABC में

\angle A+\angle B+\angle C=180^{\circ} \cdots(1)
(त्रिभुज के तीनों कोणों का योग 180° होता है)
\triangle DEF में

\angle D+\angle E+\angle F=180^{\circ} \cdots(2)
(त्रिभुज के तीनों कोणों का योग 180° होता है)
समीकरण (1) तथा (2) सेः
\angle A+\angle B+\angle C=\angle D+\angle E+\angle F \\ \Rightarrow \angle C=\angle F [ \because \angle A=\angle D, \angle B=\angle E(दिया है)]
अतः \triangle ABC \text { और } \triangle DEF में
\angle A=\angle D, \angle B=\angle E और \angle C=\angle F \\ \Rightarrow \triangle ABC व \triangle DEF समान कोणिक हैं।

\Rightarrow \triangle ABC \sim \triangle DEF
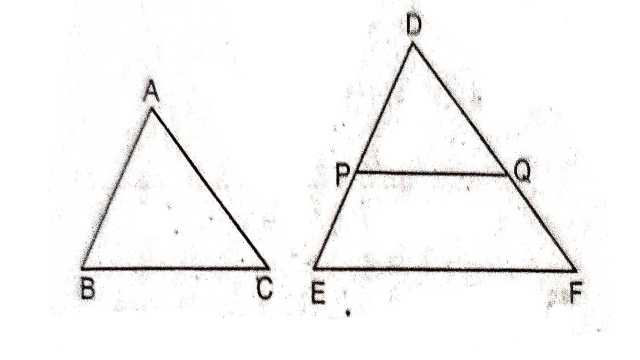
प्रमेय (Theorem):6.4.यदि दो त्रिभुजों में एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती (अर्थात् एक ही अनुपात में) हों तो इनके संगत कोण बराबर होते हैं और इसलिए दोनों त्रिभुज समरूप होते हैं।

दिया है (Given): \triangle ABC एवं \triangle DEF में

\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}
सिद्ध करना है (To Prove): \triangle ABC \sim \triangle DEF
रचना (Construction):DE एवं DF पर बिन्दु P एवं Q लेकर दोनों को मिलाया जहाँ DP=AB एवं DQ=AC हो।
उपपत्ति (Proof): \triangle ABC एवं \triangle DEF में,

\frac{A B}{D E}=\frac{A C}{D F}=\frac{B C}{E F} \ldots(1)
एवं \frac{A B}{D P}=\frac{A C}{D Q} (रचना से)
(1) व (2) सेः

\frac{DP}{DE}=\frac{DQ}{DF}
आधारभूत आनुपातिकता प्रमेय सेः

PQ \| EF \\ \angle DPQ=\angle DEF
एवं \angle DQP=\angle DFE
अतः कोण-कोण-कोण समरूपता गुणधर्म सेः

\triangle DPQ \sim \triangle DEF \cdots(3)
अर्थात् समरूप त्रिभुजों \triangle DPQ एवं \triangle DEF की संगत भुजाएँ समानुपाती होंगी अर्थात्

\frac{D P}{D E}=\frac{P Q}{E F} \\ \Rightarrow \frac{A B}{D E}=\frac{P Q}{E F} \cdots(4)
समीकरण (1) व (4) सेः

\frac{P Q}{E F}=\frac{B C}{E F} \\ \Rightarrow PQ=BC \cdots(5)
अब \triangle ABC एवं  \triangle DPQ में
AB=DP (रचना से)
AC=DQ (रचना से)
BC=PQ [(5) से]
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से

\triangle ABC \cong \triangle DPQ
सर्वांगसम त्रिभुज समरूप भी होते हैं

\triangle ABC \sim \triangle DPQ \cdots(6)
समीकरण (3) व (6) सेः

\triangle ABC \sim \triangle DPQ \sim \triangle DEF \\ \Rightarrow \triangle ABC \sim \triangle DEF
प्रमेय (Theorem):6.5.यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों के अन्तर्गत करने वाली भुजाएँ समानुपाती हों तो दोनों त्रिभुज समरूप होते हैं।

दिया है (Given): \triangle ABC एवं \triangle DEF में
\frac{A B}{D E}=\frac{A C}{D F} एवं \angle A=\angle D
सिद्ध करना है (To Prove): \triangle ABC \sim \triangle DEF
रचना (Construction):की भुजा DE एवं DF पर बिन्दु P और Q लेकर दोनों को मिलाया जहाँ AB=DP एवं AC=DQ हों।
उपपत्ति (Proof): \triangle ABC एवं \triangle DPQ में
AB=DP (रचना से)
AC=DQ (रचना से)
\angle A=\angle D (दिया है)
अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से
\triangle ABC \cong \triangle DPQ \cdots(1) \\ \frac{A B}{D E}=\frac{A C}{D F} (दिया है)
एवं \frac{A B}{D P}=\frac{A C}{D Q} (रचना से)……(3)
समीकरण (2) व (3) सेः

\frac{D P}{D E}=\frac{D Q}{D F}
अतः आधारभूत आनुपातिकता प्रमेय के विलोम से

P Q \| E F \\ \angle DPQ=\angle E \\ \angle DQP=\angle F
अतः कोण-कोण समरूपता से

\triangle DPQ \sim \triangle DEF \cdots(4)
समीकरण (1) व (4) से

\triangle ABC \sim \triangle DPQ \\ \Rightarrow \triangle ABC \sim \triangle DEF
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Tangent to a Circle Class 10

2.त्रिभुजों की समरूपता के लिए कसौटियाँ के साधित उदाहरण (Criteria for Similarity of Triangles Solved Examples):

Example:1.बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौनसे युग्म समरूप हैं।उस समरूपता कसौटी को लिखिए जिसका आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
Example:1(i).

Solution: \triangle ABC \text { तथा } \triangle PQR में
\angle A=\angle P=60^{\circ} (दिया है)
\angle B=\angle Q=80^{\circ}  (दिया है)
\angle C=\angle R=40^{\circ} (दिया है)
AAA समरूपता नियम से

\triangle ABC \sim \triangle PQR
Example:1(ii).

Solution: \triangle ABC \text { तथा } \triangle QRP में

\frac{A B}{Q R}=\frac{2}{4}=\frac{1}{2}, \frac{B C}{P R}=\frac{2.5}{5}=\frac{1}{2}, \frac{A C}{P Q}=\frac{3}{6}=\frac{1}{2}
अतः \frac{A B}{Q R}=\frac{B C}{P R}=\frac{A C}{P Q}=\frac{1}{2}
SSS समरूपता नियम से

\triangle ABC \sim \triangle QRP
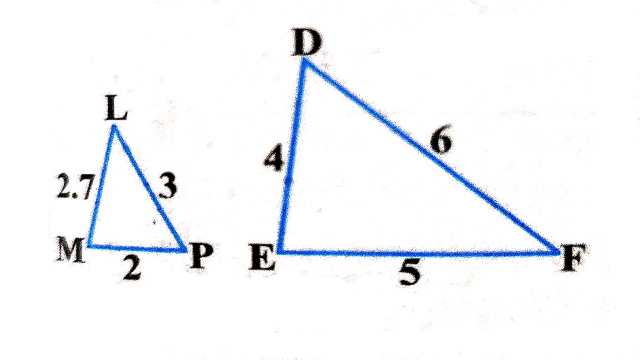
Example:1(iii).

Solution: \triangle LMP तथा \triangle FED में

\frac{M P}{E D}=\frac{2}{4}=\frac{1}{2}, \frac{P L}{D F}=\frac{3}{6}=\frac{1}{2} \\ \frac{L M}{F E}=\frac{2.7}{5}=\frac{27}{50} \\ \frac{M P}{E D}=\frac{P L}{D F} \neq \frac{L M}{F E}

दोनों त्रिभुजों की भुजाएँ समानुपात में नहीं है अतः \triangle LMP \not \sim \triangle FED
Example:1(iv).

Solution: \triangle LMN तथा \triangle RQR में
\frac{L M}{R Q}=\frac{5}{10}=\frac{1}{2}, \angle M=\angle Q=70^{\circ}, \frac{MN}{Q P}=\frac{2.5}{5}=\frac{1}{2} \\ \Rightarrow \frac{L M}{R Q}=\frac{M N}{Q P}=\frac{1}{2} तथा \angle M=\angle Q=70^{\circ}
SAS समरूपता नियम से

\triangle LMN \sim \triangle RQP
Example:1(v).

Solution: \triangle ABC तथा \triangle DFE  में

\frac{A B}{DF}=\frac{2.5}{5}=\frac{1}{2}, \frac{B C}{E F}=\frac{3}{6}=\frac{1}{2}, \angle B \neq \angle F 
अतः \triangle ABC \not \sim \triangle DFE (दोनों त्रिभुज समरूप नहीं हैं)
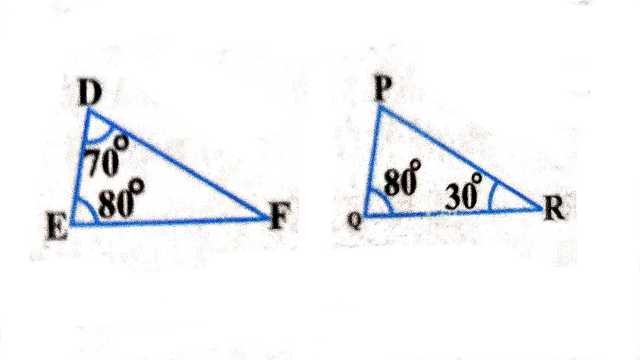
Example:1(vi).

Solution: \triangle DEF में

\angle D=70^{\circ}, \angle E=80^{\circ}, \angle F=? \\ \angle D+\angle E+\angle F=180^{\circ} \\ \Rightarrow 70+80^{\circ}+\angle F=180^{\circ} \\ \Rightarrow \angle F=180^{\circ}-150^{\circ} \\ \Rightarrow \angle F=30^{\circ} \\ \triangle PQR में

\angle Q=80^{\circ}, \angle R=30^{\circ}, \angle P=? \\ \angle P+\angle Q+\angle R=180^{\circ} \\ \Rightarrow \angle P+80^{\circ}+30^{\circ}=180^{\circ} \\ \Rightarrow \angle P=180^{\circ}-110^{\circ} \\ \Rightarrow \angle P=70^{\circ} \\ \triangle DEF  तथा \triangle PQR  में

\angle D=\angle P=70^{\circ} \\ \angle E=\angle Q=80^{\circ} \\ \angle F=\angle R=30^{\circ}
AAA समरूपता नियम से

\triangle DEF \sim \triangle PQR
Example:2.आकृति में \triangle ODC \sim \triangle OBA ,\angle BOC=125^{\circ} और \angle CDO=70^{\circ} है। \angle DOC, \angle DCO और \angle OAB ज्ञात कीजिए।
Solution:

\angle DOC+\angle BOC=180^{\circ}
(रैखिक कोण युग्म से)
\Rightarrow \angle DOC+125^{\circ}=180^{\circ} \\ \Rightarrow \angle DOC= 180^{\circ}-125^{\circ} \\ \Rightarrow \angle DOC=55^{\circ} \\ \triangle DOC में
\angle DOC+\angle CDO+\angle DCO=180^{\circ} \\ \Rightarrow 55^{\circ}+70^{\circ}+\angle DCO=180^{\circ} \\ \Rightarrow \angle DCO=180^{\circ}-125^{\circ} \\ \Rightarrow \angle DCO= 55^{\circ} \\ \triangle ODC \sim \triangle OBA (दिया है)

\angle OAB=\angle OCD \\ \Rightarrow \angle OAB=55^{\circ}
अतः \angle DOC=55^{\circ}, \angle DCO=55^{\circ}, \angle OAB=55^{\circ}
Example:3.समलम्ब ABCD जिसमें AB \| CD है,के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए,दर्शाइए कि \frac{O A}{O C}=\frac{O B}{O D} है।
Solution:दिया है (Given):ABCD एक समलम्ब चतुर्भुज है जिसमें A B \| C D तथा उसके विकर्ण AC और BD बिन्दु O पर काटते हैं।

सिद्ध करना है (To Prove): \frac{O A}{O C}=\frac{O B}{O D}
उपपत्ति (Proof): AB \| CD तथा AC व BD तिर्यक रेखा इनको काटती है अतः
\angle OAB=\angle OCD (एकान्तर कोण)…….(1)
\angle OBA=\angle ODC(एकान्तर कोण)……..(2)

\triangle AOB \text { तथा } \triangle COD में
\angle OAB=\angle OCD [(1) से]
\angle OBA=\angle ODC [(2) से]
\angle AOB=\angle COD (शीर्षाभिमुख कोण)
कोण-कोण-कोण समरूपता से

\triangle AOB \sim \triangle COD \\ \Rightarrow \frac{O A}{O C}=\frac{O B}{O D}
(समरूप त्रिभुजों की भुजाएँ समानुपाती होती हैं)
Example:4.आकृति में, \frac{Q R}{Q S}=\frac{Q T}{P R} तथा \angle 1= \angle 2 है।दर्शाइए कि \triangle PQS \sim \triangle TQR है।
Solution:

दिया है (Given): \frac{Q R}{Q S}=\frac{Q T}{P R} तथा \angle 1=\angle 2
सिद्ध करना है (To Prove): \triangle PQS \sim \triangle TQR
उपपत्ति (Proof): \triangle PQR में
\angle 1=\angle 2 (दिया है)
अतः PQ=PR (त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती है)……(1)
\frac{Q R}{Q S}=\frac{Q T}{P R} (दिया है)
\frac{Q R}{Q S}=\frac{Q T}{P Q} [(1) से]
\Rightarrow \frac{Q S}{Q R}=\frac{P Q}{Q T} (विलोमानुपात से)…….(2)
\triangle PQS तथा \triangle TQR में
\frac{Q S}{Q R}=\frac{P Q}{T Q} [(2) से]
\angle 1=\angle 1 (उभयनिष्ठ है)
SAS समरूपता नियम से

\triangle PQS \sim \triangle TQR
Example:5. \triangle PQR की भुजाओं PR और QR पर क्रमशः बिन्दु S और T इस प्रकार स्थित हैं कि \angle P=\angle RTS है।दर्शाइए कि \triangle RPQ \sim \triangle RTS है।
Solution:

दिया है (Given): \triangle PQR की भुजाओं PR और QR पर क्रमशः बिन्दु S और T इस प्रकार स्थित हैं कि \angle P=\angle RTS
सिद्ध करना है (To Prove): \triangle RPQ \sim \triangle RTS
उपपत्ति (Proof): \triangle RPQ तथा \triangle RTS में
\angle RPQ=\angle RTS (दिया है)
\angle PRQ=\angle TRS (उभयनिष्ठ है)
अतः AA समरूपता नियम से

\triangle RPQ \sim \triangle RTS
Example:6.आकृति में,यदि \triangle ABE \cong \triangle ACD है तो दर्शाइए कि \triangle ADE \sim \triangle ABC है।
Solution:

दिया है (Given): \triangle ABE \cong \triangle ACD
सिद्ध करना है (To Prove): \triangle ADE \sim \triangle ABC
उपपत्ति (Proof): \triangle ABE \cong \triangle ACD
AD=AE (CPCT) …..(1)
तथा AB=AC (CPCT)…. (2)
समीकरण (1) में (2) का भाग देने पर

\frac{A D}{A B}=\frac{A E}{A C} \ldots(3) \\ \triangle ADE तथा \triangle ABC में
\frac{A D}{A B}=\frac{A E}{A C} [(3) से]
\angle A=\angle A (उभयनिष्ठ है)
SAS समरूपता नियम से

\triangle ADE \sim \triangle ABC
Example:7.आकृति में \triangle ABC के शीर्ष लम्ब AD और CE परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।दर्शाइए किः

(1) \triangle AEP \sim \triangle CDP
(ii) \triangle ABD \sim \triangle CBE
(ii) \triangle AEP \sim \triangle ADB
(iv) \triangle PDC \sim \triangle BEC
Solution:

दिया है (Given): \triangle ABC में AD \perp CB व CE \perp AB
सिद्ध करना है (To Prove):(1) \triangle AEP \sim \triangle CDP
(ii) \triangle ABD \sim \triangle CBE
(ii) \triangle AEP \sim \triangle ADB
(iv) \triangle PDC \sim \triangle BEC
उपपत्ति (Proof):(i) \triangle AEP तथा \triangle CDP में
\angle AEP=\angle CDP=90^{\circ} (दिया है)
\angle APE=\angle CPD (शीर्षाभिमुख कोण)
AA समरूपता से

\triangle AEP \sim \triangle CDP
(ii) \triangle ABD तथा \triangle CBE में
\angle ADB=\angle CEB=90^{\circ} (दिया है)
\angle ABD=\angle CBE (उभयनिष्ठ है)
AA समरूपता नियम से

\triangle ABD \sim \triangle CBE
(iii) \triangle AEP तथा \triangle ADB में
\angle AEP=\angle ADB=90^{\circ}(दिया है)
\angle EAP=\angle DAB (उभयनिष्ठ है)
AA समरूपता से

\triangle AEP \sim \triangle ADB
(iv) \triangle PDC तथा \triangle BEC में
\angle PDC=\angle BEC=90^{\circ} (दिया है)
\angle PCD=\angle BCE  (उभयनिष्ठ है)
AA समरूपता से

\triangle PDC \sim \triangle BEC
Example:8.समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है।दर्शाइए कि \triangle ABE \sim \triangle CFB है।
Solution:

दिया है (Given):समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर बिन्दु पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove): \triangle ABE \sim \triangle CFB
उपपत्ति (Proof): \triangle ABE तथा \triangle CFB में
\angle A=\angle C (समान्तर चतुर्भुज के सम्मुख कोण)
\angle AEB=\angle CBF (एकान्तर कोण)
AA समरूपता से

\triangle ABE \sim \triangle CFB
Example:9.आकृति में ABC और AMP दो समकोण त्रिभुज हैं जिनके कोण B और M समकोण हैं सिद्ध कीजिए किः

(i) \triangle ABC \sim \triangle AMP
(ii) \frac{C A}{P A}=\frac{B C}{M P}
Solution:

दिया है (Given): \triangle ABC तया \triangle AMP में \angle B=\angle M=90^{\circ}
सिद्ध करना है (To Prove): (i) \triangle ABC \sim \triangle AMP
(ii) \frac{C A}{P A}=\frac{B C}{M P}
उपपत्ति (Proof):(i)\triangle ABC तथा \triangle AMP में
\angle BAC=\angle MAP (उभयनिष्ठ है)
\angle ABC=\angle AMP=90^{\circ} (दिया है)
AA समरूपता से

\triangle ABC \sim \triangle AMP
(ii) \triangle ABC \sim \triangle AMP (सिद्ध किया है)
\frac{C A}{P A}=\frac{B C}{M P}(समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
उपर्युक्त उदाहरणों द्वारा त्रिभुजों की समरूपता के लिए कसौटियाँ (Criteria for Similarity of Triangles),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) को समझ सकते हैं।

3.त्रिभुजों की समरूपता के लिए कसौटियाँ पर आधारित सवाल (Questions Based on Criteria for Similarity of Triangles):

(1.)यदि दो त्रिभुज समरूप हों तो सिद्ध कीजिए कि संगत भुजाएँ संगत ऊँचाइयों के अनुपात में होंगी।
(2.)यदि एक समकोण त्रिभुज में समकोण बनाने वाले शीर्ष से कर्ण पर डाला जाए तो सिद्ध कीजिए कि इस लम्ब के दोनों ओर बने त्रिभुज परस्पर समरूप होंगे तथा ये दोनों त्रिभुज उस मूल त्रिभुज के भी समरूप होंगे जिसके ये दो भाग हैं।
(3.)दी गई आकृति में \triangle BEP एवं \triangle CDP समकोण त्रिभुज हों तो सिद्ध कीजिए किः BP \times PD=EP \times PC 

उपर्युक्त सवालों को हल करने पर त्रिभुजों की समरूपता के लिए कसौटियाँ (Criteria for Similarity of Triangles),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) को ठीक से समझ सकते हैं।

Also Read This Article:-Tangent to Circle Class 10

4.त्रिभुजों की समरूपता के लिए कसौटियाँ (Frequently Asked Questions Related to Criteria for Similarity of Triangles),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Criteria for Similarity of Triangles

त्रिभुजों की समरूपता के लिए कसौटियाँ
(Criteria for Similarity of Triangles)

Criteria for Similarity of Triangles