Correlation by Method of Least Squares
1.न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Correlation by Method of Least Squares),सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation by Concurrent Deviation Method in Statistics):
न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Correlation by Method of Least Squares) न्यूनतम वर्ग विधि के अनुसार खींची गई सर्वोत्कृष्ट रेखा (Line of best fit) पर आधारित है।न्यूनतम वर्ग रेखा,प्रसामान्य समीकरणों (Normal Equations) की सहायता से खींची जाने वाली एक सर्वोपयुक्त उपयुक्तता रेखा (Estimating line of the best fit) है जिसके लक्षण होते हैं
(i)अवलोकित मूल्यों (y) और उक्त रेखा से संगणित तत्संवादी मूल्यों (y_{c}) का योग शून्य होता है,अर्थात् \Sigma(y-y_{c})=0
(ii)इस रेखा द्वारा संगणित मूल्यों के अवलोकित मूल्यों (y_{c}) के विचलनों के वर्गों का योग,अन्य किसी भी रेखा से निकाले गए विचलनों के वर्गों की तुलना में न्यूनतम होता है।अतः इसे न्यूनतम वर्ग रीति के नाम से संबोधित करते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Spearman Rank Difference Method
2.न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध के उदाहरण (Correlation by Method of Least Squares Examples):
Example:1.निम्नलिखित समंकों से न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध गुणांक ज्ञात कीजिएः
(From the following data,calculate coefficient of correlation by the least squares method):
![]()
Solution:Calculation of Computed Values of Y by Least Squares
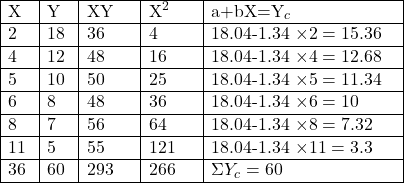
\Sigma X=N a+b \Sigma X \\ 60=6 a+36 b \cdots(1) \\ \Sigma XY \equiv a \Sigma X+b \Sigma X^2 \\ 293=36 a+266 b \cdots(2)
समीकरण (1) को (6) से गुणा करने परः
360=36 a+216 b \cdots(3)
समीकरण (3) में से (2) घटाने परः
67=-50 b \Rightarrow b=\frac{67}{-50}=-1.34
b का मान समीकरण (1) में रखने परः
Computation of S y^{2} and \sigma y^{2 }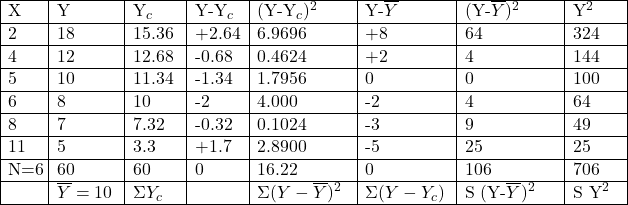
Example:2.निम्न आंकड़ों से न्यूनतम वर्ग विधि द्वारा सहसम्बन्ध गुणांक,निश्चयन गुणांक तथा असहसम्बन्ध गुणांक ज्ञात कीजिएः
(From the following data compute r,the coefficient of determination and coefficient of alienation by method of least squares):
![]()
Solution:Calculation of Computed Values of Y by Least-Squares

\Sigma Y=N a+b \Sigma x \\ 1260=7 a+28 b \cdots(1) \\ \Sigma X Y=a \Sigma x+b \Sigma x^2 \\ 5152=28 a+140 b \cdots(2)
समीकरण (1) को 4 से गुणा करने परः
5040=28 a+112 b \cdots(3)
समीकरण (2) में से (3) घटाने परः
132=28 b \Rightarrow b=\frac{112}{28}=4
b का मान समीकरण (1) में रखने परः
1260=7 a+28 \times 4 \\ \Rightarrow 7 a=1260-112 \Rightarrow a=\frac{1148}{7} \\ \Rightarrow a=164
Computation of S y^{2} and \sigma_{y^{2 }}
S_{y^2}=\frac{\Sigma\left(Y-Y_{c}\right)^2}{N}=\frac{568}{7}=81.1429 \\ \sigma_{y^{2}} =\frac{\Sigma (Y-\bar{Y})^2}{N}=\frac{1016}{7}=145.1429 \\ r=\sqrt{\left[1-\frac{S_{y^2}}{\sigma_y^2}\right]}=\sqrt{1-\frac{81.1429}{145.1429}} \\ =\sqrt{\frac{145.1429-81.1429}{145.1429}} \\ =\sqrt{\frac{64}{145.5264}}=\sqrt{0.440944}\\ =0.66403 \\ r \approx+0.66 (b का मान धनात्मक है अतः सहसम्बन्ध गुणांक धनात्मक होगा)
निश्चयन गुणांक C of D=r^2 \\ =0.66^2=0.4356 \\ \approx+0.44
अनिश्चयन गुणांक k=\sqrt{1-r^2} \\ =\sqrt{1-(0.44)} \\ =\sqrt{0.56} \\ =0.7483 \\ k \approx+0.75
3.सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक के उदाहरण (Coefficient of Correlation by Concurrent Deviation Method in Statistics Examples):
Example:45.निम्नलिखित समंकों से संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक ज्ञात कीजिएः
(Calculate Coefficient of Concurrent deviation from the following data):

Solution:Calculation Table of Coefficient of Correlation by Concurrent Deviation Method
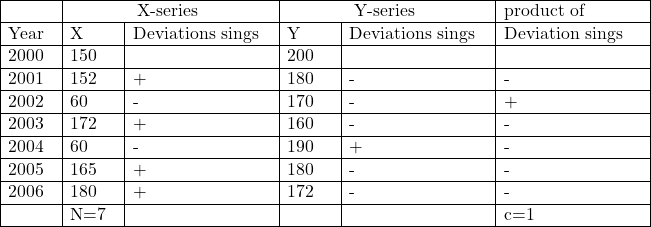
r(c)= \pm \sqrt{ \pm\left(\frac{2 c-N}{N}\right)} \\ = \pm \sqrt{ \pm\left(\frac{2 \times 1-6}{7}\right)} \\ =-\sqrt{-\left ( -\frac{4}{7} \right )} \\ =-\sqrt{\frac{4}{7}}=-\sqrt{0.66667} \\ =-0.81649 \\ \Rightarrow r(c) =-0.8165
Example:46.संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक ज्ञात कीजिए:
(Find out coefficient deviation method from the following data):

Solution:Calculation Table of Coefficient of Correlation by Concurrent Deviation Method
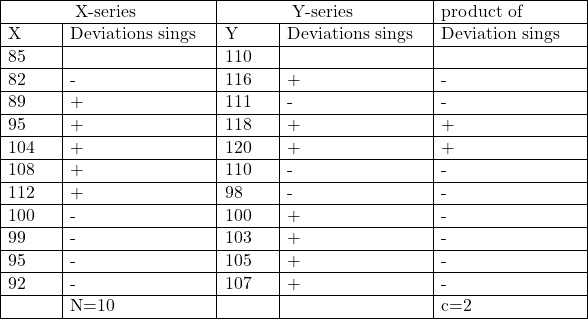
r(c)= \pm \sqrt{ \pm\left(\frac{2 C-N}{N}\right)} \\ = \pm \sqrt{ \pm\left(\frac{2 \times 2-10}{10}\right)} \\ = \pm \sqrt{ \pm\left(\frac{4-10}{10}\right)} \\ =-\sqrt{-\left(-\frac{6}{10}\right)} \\=-\sqrt{\frac{3}{5}}=-\sqrt{0.6} \\ =-0.77459 \\ r(c) \approx-0.77
Example:47.सहसम्बन्ध गुणांक से क्या तात्पर्य है? निम्न आँकड़ों से संगामी विचलन रीति से सहसम्बन्ध गुणांक की गणना करो।
(What is meant by correlation? Calculate the coefficient of concurrent deviations from the following data):

Solution:Calculatuon Table of Coefficient of Correlation by Concurrent Deviation Method
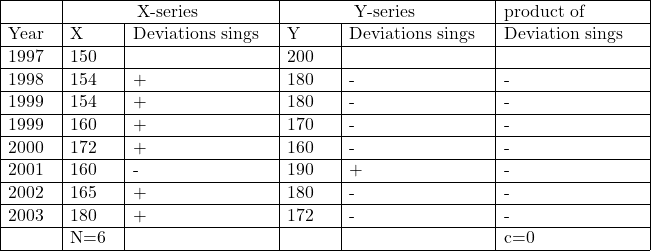
r(c)= \pm \sqrt{ \pm\left(\frac{2 C-N}{N}\right)} \\ = \pm \sqrt{ \pm\left(\frac{2 \times 0-6}{6}\right)} \\ = \pm \sqrt{ \pm\left(-\frac{6}{6}\right)} \\ =-\sqrt{-(-1)} \\ \Rightarrow r(c)=-1
Example:49(i).यदि एक्स तथा वाई के मध्य सह-विचरण की मात्रा 9.6 तथा एक्स व वाई के प्रसरण क्रमशः 16 व 9 हों तो सहसम्बन्ध गुणांक ज्ञात कीजिएः
(If covariance between x and y variable is 9.6 and variance of x and y variables are 16 and 9 respectively.Find coefficient of correlation.)
Solution: corviance =\frac{\Sigma x y}{N}=9.6 \\ \sigma_x^2=16 \Rightarrow \sigma_x=4, \sigma_y^2=9 \Rightarrow \sigma_y=3 \\ r=\frac{\text { Covariance }}{\sigma_x \cdot \sigma_y} \\ =\frac{9.6}{4 \times 3}=\frac{9.6}{12} \Rightarrow r=0.8
Example:49(ii).पति तथा पत्नी की आयु में सहसम्बन्ध के अध्ययन हेतु पति तथा पत्नियों के समग्र में से 104 युग्मों का चयन किया गया।उनका सहसम्बन्ध गुणांक +0.9 पाया गया।समग्र के सहसम्बन्ध गुणांक की सीमाएँ क्या हैं?
(The study the correlation between the ages of husbands and wives a sample of 104 pairs is taken from the universe.It gives the coefficient of correlation between variables to be +0.9.Within what limits it hold true for the universe)
Solution: N=104, r=+0.9
S.E. of r =\frac{1-r^2}{N} \\ =\frac{1-(0.9)^2}{104} \\ =\frac{1-0.81}{104}=\frac{0.19}{104} \\ \Rightarrow S.E. of r =0.001826
Limits it hold =r \pm 3 \text{S.E.} \\ =0.9 \pm 0.001826
0.898174 to 0.901826
उपर्युक्त उदाहरणों के द्वारा न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Correlation by Method of Least Squares),सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation by Concurrent Deviation Method in Statistics) को समझ सकते हैं।
4.सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक की समस्याएं (Coefficient of Correlation by Concurrent Deviation Method in Statistics Problems):
(1.)निम्न आंकड़े एक फैक्ट्री के 11 मजदूरों की आय व खर्चे के सम्बन्ध में दिए गए हैं।संगामी विचलन विधि के द्वारा मालूम कीजिए कि आय और खर्चे में क्या कोई सहसम्बन्ध है?
(The following data relate to the income and expenditure of 11 workers of a factory.Find,by concurrent deviations method,whether there is any correlation between income and expenditure):

(2.)निम्न आँकड़ों से संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक निकालिएः
(Calculate the coefficient of concurrent deviation from the data given below):

Answers:- (1.)r_{c}=+0.89
(2.) r_c=-1
उपर्युक्त सवालों को हल करने पर न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Correlation by Method of Least Squares),सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation by Concurrent Deviation Method in Statistics) को ठीक से समझ सकते हैं।
Also Read This Article:-Coefficient of Correlation
5.न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Frequently Asked Questions Related to Correlation by Method of Least Squares),सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation by Concurrent Deviation Method in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.संगामी रीति से क्या तात्पर्य है? (What Do You Mean by Concurrent Deviation Method?):
उत्तर:कभी-कभी दो श्रेणियों के मध्य सहसंबंध की वास्तविक मात्रा जानने की आवश्यकता नहीं होती बल्कि केवल यह जानने की आवश्यकता है कि सहसंबंध किस दिशा में है अर्थात् धनात्मक है या ऋणात्मक है।ऐसी दशा में यह रीति उपयोगी रहती है।यह रीति बिंदु रेखीय रीति पर आधारित है।बिंदु रेखीय रीति सम्बद्ध समंक श्रेणियों के वक्र एक ही दिशा में साथ-साथ गमन करते हैं या संगामी हैं तो उनमें धनात्मक सहसंबंध होता है।यदि वक्र विपरीत दिशा में गमन करते हैं अर्थात् प्रतिगामी है तो उनमें ऋणात्मक सहसंबंध पाया जाता है।इसी प्रकार संगामी विचलन रीति के अनुसार भी यदि समंक श्रेणियों के अधिकतर विचलन संगामी (concurrent) होते हैं तो उनमें धनात्मक सहसंबंध होता है तथा यदि ये विचलन प्रतिगामी (Divergent) होते हैं तो उनमें ऋणात्मक सहसंबंध होता है।
प्रश्न:2.संगामी विचलन रीति द्वारा सहसम्बन्ध की गणना क्रिया विधि लिखिए। (Write Working Rule of Calculating the Correlation by Concurrent Deviation Method):
उत्तर:(1.)प्रत्येक श्रेणी में अगले पद मूल्य की उससे बिल्कुल पूर्व (previous) के पद मूल्य से तुलना की जाती है।यदि मूल्य पिछले मूल्य से अधिक है तो उसका विचलन (+) होगा यदि मूल्य गत मूल्य से कम है तो उसका विचलन (-) तथा यदि बराबर है तो विचलन (=) होगा।यह ध्यान रखा जाना चाहिए कि इस रीति में विचलन का केवल चिन्ह ही लिखा जाता है,विचलन की मात्रा नहीं।विचलन युग्मों की संख्या श्रेणी में दिए गए पद-युग्मों की संख्या से एक कम होती है।
(2.)X तथा Y श्रेणियों के विचलन चिन्हों के आधार पर संगामी प्रवृत्ति ज्ञात की जाती है।जिन पद-युग्मों में एक साथ वृद्धि,कमी या बराबरी रही है उनके सामने (+) चिन्ह लगाते हैं।ऐसे मदों के योग को संकेताक्षर ‘c’ द्वारा व्यक्त किया जाता है।
(3.)फिर निम्न सूत्र का प्रयोग किया जाता हैः
r_{c}= \pm \sqrt{ \pm \frac{2 C-N}{N}}
सूत्र में प्रयुक्त संकेताक्षरः
r_{c}=coefficient of concurrent deviation
c=Number of concurrent deviation
N=Number of pairs of observation
सूत्र में (\pm) चिन्हों का महत्त्वः
सूत्र में वास्तविक चिन्ह से पहले तथा वर्गमूल के अंदर (\pm) चिन्हों का प्रयोग किया गया है।यदि (2c-N) धनात्मक है तो दोनों स्थानों पर (+) चिन्ह का प्रयोग किया जाएगा।इसके विपरीत यदि (2c-N) ऋणात्मक है तो दोनों स्थानों पर (-) चिन्ह का प्रयोग किया जाएगा।यदि ऐसा न किया जाए तो वर्गमूल चिन्ह के अन्दर की राशि ऋणात्मक ही रहेगी,जिसका वर्गमूल ज्ञात करना सम्भव नहीं होगा।
प्रश्न:3.संग्रामी विचलन रीति की विशेषताएं लिखिए (Write the Characteristics of Concurrent Deviation Method):
उत्तर:(1.)यह रीति सहसंबंध ज्ञात करने की सरलतम रीति है तथा मध्यकालीन उच्चावचनों के संबंध का अध्ययन करने के लिए उपयुक्त है।
(2.)इस रीति में प्रत्येक पद मूल्य के विचलन उससे बिल्कुल पहले वाले पद-मूल्य से तुलना कर प्राप्त किए जाते हैं।
(3.)इस रीति में सहसंबंध की दिशा का ही अध्ययन किया जाता है,मात्रा का नहीं।
प्रश्न:4.संगामी विचलन रीति के दोष लिखिए। (Write the Demerits of Concurrent Deviation Method):
उत्तर:(1.)इस रीति में सहसम्बन्ध की मात्रा का अध्ययन नहीं किया जाता है।
(2.)दीर्घकालीन प्रवृत्ति के संबंध में यह रीति अनुपयुक्त है।
उपर्युक्त दोषों के कारण इस विधि का प्रयोग सीमित क्षेत्र में ही होता है।
प्रश्न:5.न्यूनतम वर्ग विधि द्वारा सहसम्बन्ध की गणना क्रिया विधि लिखिए। (Write the Working Rule of Calculating the Correlation by Method of Least-Squares):
उत्तरःसर्वप्रथम समीकरण y=a+bx में a व b का मान ज्ञात करने हेतु दो सामान्य समीकरणों (Normal Equations) का प्रयोग करते हैं।यह निम्नलिखित हैः
(1.) \Sigma y=N a+b \Sigma x व (2.) \Sigma x y=a \Sigma x+b \Sigma x^2
यहां पर \Sigma y=y श्रेणी के मूल्यों का योग,N=पद युग्मों की संख्या, \Sigma x=x श्रेणी का योग, \Sigma xy=x तथा y के गुणनफलों का योग, \Sigma x^{2}=x श्रेणी के पदों के वर्गों का योग।
(2.)उपर्युक्त दोनों समीकरणों को हल करके ‘a’ तथा ‘b’ के मान ज्ञात करते हैं।
(3.)’a’ व ‘b’ के मानों को उपनति समीकरण (Trend Equation) में प्रतिस्थापित कर देते हैं।
(4.)उपनति समीकरण में x पद के मूल्यों के आधार पर y के विभिन्न मूल्यों की संगणना की जाती है।इस प्रकार ज्ञात मूल्यों का योग y श्रेणी के प्रस्तुत मूल्यों के बराबर होगा।
(5.)y के प्रस्तुत मूल्यों में तत्संबंधित y के संगणित मूल्य घटाकर विचलन प्राप्त करते हैंः d=\left(y-y_c\right)
(6.)इस प्रकार प्राप्त विचलनों के वर्गों का योग कर लेंगे।
(7.)तत्पश्चात उपर्युक्त \Sigma \left(y-y_c\right)^2 लिए गए विचलनों का माध्य ज्ञात करते हैं,अर्थात् \Sigma y^2=\frac{\Sigma (y-y)^2}{N} सर्वोपयुक्त रेखा का प्रसरण (variance) है जिसे अस्पष्टीकृत प्रसरण (unexplained variance) भी कहते हैं।यह माप इस बात का संकेत देता है कि किस सीमा तक y में होने वाले परिवर्तन x के परिवर्तनों से अप्रभावित रहते हैं।
(8.)अन्त में निम्न सूत्र के प्रयोग से सहसम्बन्ध गुणांक ज्ञात हो जायेगाः
r=\sqrt{\left[1-\frac{S_{y^2}}{\sigma_y^2}\right]}
यदि b का चिन्ह ऋणात्मक है तो सहसम्बन्ध भी ऋणात्मक होगा तथा b का मान धनात्मक होने पर r भी धनात्मक होगा।
प्रश्न:6.सहसम्बन्ध में विलम्बन और अग्रगमन से क्या तात्पर्य है? (What Do You Mean by Lag and Lead in Correlation?):
उत्तर:साधारणत: यह देखने में आता है किसी कारण का प्रभाव कुछ समय पश्चात पड़ता है।कारण और प्रभाव के मध्य के समय को विलंबन (Lag) कहते हैं।कारण और प्रभाव में समयान्तर का प्रमुख कारण यह है कि कारण का घटना के होने पर उसका प्रभाव होते-होते समय लगता है।उदाहरणार्थ मुद्रा में प्रसार होने के कुछ समय पश्चात वस्तुओं के मूल्य में वृद्धि होती है।इसी प्रकार मुद्रा संकुचन होने पर वस्तुओं के मूल्य में कमी होते-होते कुछ समय लग जाता है।वैसे मुद्रा प्रसार तथा मूल्यों में वृद्धि के मध्य उच्च कोटि का धनात्मक संबंध ही प्रत्याशित है परंतु कारण और प्रभाव के बीच समयान्तर होने के कारण सहसंबंध उस मात्रा या कोटि का नहीं होगा जैसाकि वास्तव में है।यदि मुद्रा प्रसार व मूल्यों को ग्राफ-पत्र पर अंकित किया जाय तो मुद्रा प्रसार वक्र तथा मूल्य वक्र सहसम्बन्ध की वास्तविक उच्च-कोटि का प्रदर्शन नहीं करेंगे।यह सही है कि दोनों वक्रों की दिशा समान होगी किंतु परिणाम भ्रामक होंगे क्योंकि वास्तविक स्थिति का ज्ञान नहीं हो सकेगा।ऐसी स्थिति में सहसंबंध का अध्ययन करने के लिए कारण से संबंधित समंकों को विलंबित करने की आवश्यकता होगी अर्थात् प्रभाव सम्बन्धी समंकों को कुछ आगे से चलना पड़ेगा।उस क्रिया को विलम्बन (Lag) और अग्रगमन (Lead) कहते हैं।अतः विलम्बन का अर्थ है “कारण से पिछड़ जाना तथा अग्रगमन का अर्थ है कारण का प्रभाव से पूर्व आना।”
उपर्युक्त प्रश्नों के उत्तर द्वारा न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Correlation by Method of Least Squares),सांख्यिकी में संगामी विचलन रीति द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation by Concurrent Deviation Method in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Correlation by Method of Least Squares
न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध
(Correlation by Method of Least Squares)
Correlation by Method of Least Squares
न्यूनतम वर्ग रीति द्वारा सहसम्बन्ध (Correlation by Method of Least Squares) न्यूनतम वर्ग
विधि के अनुसार खींची गई सर्वोत्कृष्ट रेखा (Line of best fit) पर आधारित है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








