1.परिरेखा समाकलन,कन्टूर समाकलन (Contour Integration)-

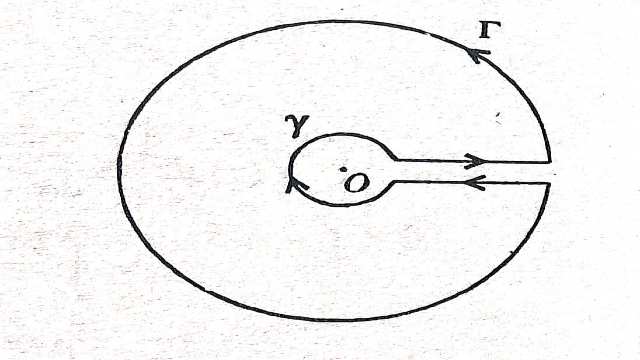
फलनों का परिरेखा समाकलन,कन्टूर समाकलन जिनके अनन्तक वास्तविक अक्ष पर हैं (Contour Integration of function having poles on the Real-axis)-यदि फलन के अनन्तक वास्तविक अक्ष पर स्थित हैं तो पूर्व में वर्णित परिरेखा समाकलन जिनके अनन्तक इकाई त्रिज्या के वृत्त के अन्दर स्थित हैं,से फलन का समाकलन नहीं किया जा सकता है। लेकिन इन अनन्तकों को टालने के लिए,इन अनन्तकों को केन्द्र मानते हुए छोटी त्रिज्या वाले अर्धवृत्तों का निर्माण करते हैं।इस प्रक्रिया को अर्धवृत्तीय परिरेखा का दन्तुरण (indenting) कहते हैं।
इस रूपान्तरित (modified) परिरेखा पर फलन विश्लेषिक रहता है तथा कोशी अवशेष प्रमेय तथा पूर्व आर्टिकल में वर्णित प्रमेयों की सहायता से समाकलन का मूल्यांकन किया जा सकता है।
बहुमानी फलनों जैसे z^{\alpha}(\alpha पूर्णांक नहीं है),\log z आदि का समाकलन भी अर्धवृत्तीय परिरेखा के दन्तुरण विधि द्वारा किया जा सकता है।इसमें शाखा बिन्दु को,उसी बिन्दु पर केन्द्रित उपरि अर्धतल में स्थित छोटी त्रिज्या वाले वृत्त द्वारा टाला जाता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Solve Complex Contour Integration

2.परिरेखा समाकलन के उदाहरण,कन्टूर समाकलन के उदाहरण (Contour Integration Examples),कन्टूर समाकलन साॅल्वड प्रोब्लमस (Contour Integration Solved Problems)-

Example-1.\int_{0}^{\infty} \frac{x^{a-1}}{1+x^{2}} d x=\frac{\pi}{2} \operatorname{cosec}\left(\frac{\pi a}{2}\right),(0<a<2)
Solution–\int_{0}^{\infty} \frac{x^{a-1}}{1+x^{2}} d x=\frac{\pi}{2} \operatorname{cosec}\left(\frac{\pi a}{2}\right)

माना \int_{c} f(z) d z=\int_{c} \frac{z^{a-1}}{1+z^{2}} d z
z^{2}+1=0 \Rightarrow z=\pm i ,f(z) के साधारण अनन्तक हैं और दोनों C के अन्दर स्थित हैं।
z=i पर अवशेष =\lim _{z \rightarrow i}(z-i) f(z) \\ =\lim _{z \rightarrow i}(z-i)\left(\frac{z^{a-1}}{1+z^{2}}\right) \\ =\lim _{z \rightarrow i} \frac{(z-i)z^{a-1}}{(z+i)(z-i)} \\ =\lim _{z \rightarrow i} \frac{z^{a-1}}{(z+i)} \\ =\frac{i^{a-1}}{2 i} \\ =\frac{i^{a-2}}{2} \\ =\frac{1}{2}\left(e^{i \pi / 2}\right)^{a-2} \\ =\frac{1}{2} e^{i(a-2) \pi / 2}
z=-i पर अवशेष=\lim _{z \rightarrow-i}(z+i) f(z) \\ =\lim _{z \rightarrow-i}(z+i) \frac{z^{a-1}}{(z+i)(z-i)} \\ =\lim _{z \rightarrow-i} \frac{z^{a-1}}{(z-i)} \\ =\frac{(-i)^{a-1}}{(-2 i)} \\ =\frac{1}{2}(-i)^{a-2} \\ =\frac{1}{2} e^{(i 3 \pi / 2)^{a-2}} \\ =\frac{1}{2} e^{3 i(a-2) \pi / 2}
अवशेषों का योग =\frac{1}{2} e^{i(a-2) \pi / 2}+\frac{1}{2} e^{3 i(a-2) \pi / 2}\\ =\frac{1}{2}\left[e^\frac {i a \pi}{2} \cdot e^{-i \pi}+e^{ \frac{i 3 a \pi}{2} \cdot e^{-i \pi}}\right]\\ =\frac{1}{2} e^{-i \pi}\left[e^{ \frac{i a \pi}{2}}+e^{ \frac{i 3 a \pi}{2}}\right]\\ =\frac{1}{2} e^{-i \pi}\left[e^{i a \pi}\left(e^{- \frac{i a \pi}{2}}+e^{\frac{i a \pi}{2}}\right)\right] \\ =-\frac{1}{2} e^{i a \pi}\left[e^{-\frac{i a \pi}{2}}+e^{\frac{i a \pi}{2}}\right] \\ =-e^{i a \pi} \cos \left(\frac{a \pi}{2}\right)
अवशेष प्रमेय से-

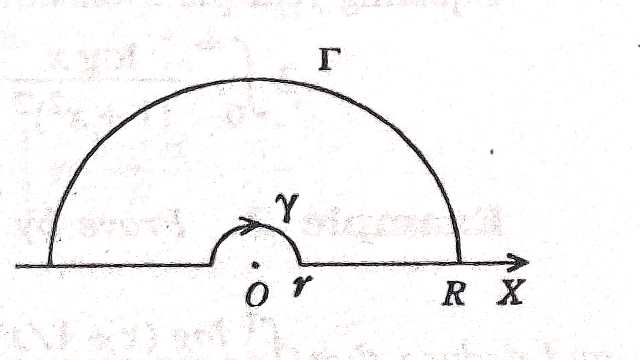
\int_{c} f(z) d z =\int_{\Gamma} f(z) d z+\int_{R}^{\rho} f\left(r e^{2 \pi i}\right) e^{i 2 \pi} dr+\int_{\gamma} f(z) d z+\int_{\rho}^{R} f(x) d x=2 \pi \sum R^{+}.....(1) \\ \left|\int_{\Gamma} f(z) d z\right| \leq \int_{0}^{2 \pi}\left|\frac{R^{a-1} e x p(a-1) i \theta}{R^{2} e^{i 2 \theta}+1} i R e^{i \theta}\right| d \theta \\ \leq \int_{0}^{2 \pi} \frac{R^{a}}{R^{2}-1} d \theta \\ \frac{2 \pi R^{a}}{R^{2}-1} \rightarrow 0 जब R \rightarrow \infty ,a>0
इसी प्रकार \left|\int_{\gamma} f(z) d z\right| \rightarrow 0 जब \rho \rightarrow 0
इस प्रकार \rho \rightarrow 0, R \rightarrow \infty समीकरण (1) से-

\int_{0}^{\infty} f(x) d x+\int_{\infty}^{0} f\left(r e^{i 2 \pi}\right) dr=2 \pi i\left\{-e^{i a \pi} \cdot \cos \left(\frac{a \pi}{2}\right)\right\} \\ \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{2}} d x-\int_{0}^{\infty} \frac{x^{a-1} e^{i(a-1) 2 \pi}}{1+x^{2}} d x=-2 \pi i e^{i a \pi} \cos \frac{a \pi}{2} \\ \Rightarrow \left(1-e^{i 2 a \pi}\right) \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{2}} d x=-2 \pi i e^{i a \pi} \cos \frac{a \pi}{2} \\ \Rightarrow \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{2}} d x =\frac{2 \pi i}{e^{i a \pi}-e^{-i a \pi}} \cos \left(\frac{a \pi}{2}\right) \\ =\frac{\pi}{\sin a \pi} \cdot \cos \left(\frac{a \pi}{2}\right) \\ \Rightarrow \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{2}} d x =\frac{\pi}{2} \operatorname{cosec} \frac{a \pi}{2}
Example-2.\int_{0}^{\infty} \frac{\log x}{\left(1+x^{2}\right)^{2}} d x=-\frac{\pi}{4}
Solution–\int_{0}^{\infty} \frac{\log x}{\left(1+x^{2}\right)^{2}} d x=-\frac{\pi}{4} \\ \int_{c} \frac{\log z}{\left(1+z^{2}\right)^{2}}=\int_{c} f(z) d z
जहां C प्रश्न में दी हुई परिरेखा है।

z^{2}+1=0 \Rightarrow z=\pm i द्विकोटि के अनन्तक हैं।
z=i पर अवशेष=\phi^{\prime}(i) \\ \phi(z) =\frac{\log z}{(z+i)^{2}} \\ \log \phi(z) =\log (\log z)-2 \log (z+i)
अवकलन करने पर-

\frac{\phi^{\prime}(z)}{\phi(z)} =\frac{1}{z \log z}-\frac{2}{z+i} \\ \Rightarrow \phi^{\prime}(z) =\phi(z)\left[\frac{1}{z \log z}-\frac{2}{z+i}\right] \\ \Rightarrow \phi^{\prime}(i) =\frac{\log i}{-4}\left[\frac{1}{i \log i}-\frac{1}{i}\right] \\ =-\frac{(1-\log i)}{4 i} \\ =-\frac{1}{4 i}\left(1-\log e^{i \pi / 2}\right) \\ =-\frac{1}{4 i} \cdot[1-i(\frac{\pi}{2})]
अवशेष प्रमेय से-

{\int_{C} f(z) d z=\int_{r}^{R} f(x) d x+\int_{\Gamma} f(z) d z+\int_{R}^{r} f\left(x e^{i \pi}\right) e^{i \pi} d x}+ \int_{\gamma} f(z) d z=2 \pi i \sum R^{+} \cdots (1) \\ \left|\int_{\Gamma} f(z) d z\right| \leq \int_{0}^{\pi}\left|\frac{\log \left(R e^{i \theta}\right)}{\left(1+R^{2} e^{i 2 \theta}\right)^{2}} R i e^{i \theta}\right| d \theta \\ \leq \int_{0}^{\pi} \frac{\log R+\theta}{\left(R^{2}-1\right)^{2}} d \theta \\ \leq \frac{\left[\pi \log R+\frac{1}{2} \pi^{2}\right] R}{\left(R^{2} -1\right)^{2}} \\ \leq \frac{\left[\pi \log R +\frac{1}{2} \pi^{2}\right] R}{\left(R^{2}-1\right)^{2}} \\ \leq \frac{R^{2}}{\left(R^{2}-1\right)^{2}}\left[\frac{\pi \log R}{R}+\frac{1}{2} \pi^{2} \frac{1}{R}\right] \rightarrow 0

जब R \rightarrow \infty \\ \lim _{R \rightarrow \infty} \frac{\log R}{R}=0
इसी प्रकार | \int_{\gamma} f(z) d z | \leq \int_{0}^{\pi} |f\left(r e^{i \theta}\right) r i e^{i \theta}| d \theta \rightarrow 0
जब r \rightarrow 0 \\ \lim _{r \rightarrow 0} r \log r=\lim_{r \rightarrow 0} \frac{\log r}{\frac{1}{r}}=0
इस प्रकार जब r \rightarrow 0, R \rightarrow \infty समीकरण (1) से-

\int_{0}^{\infty} f(x) d x -\int_{\infty}^{0} f\left(x e^{i \pi}\right) d x=2 \pi i \sum R^{+} \\ \Rightarrow \int_{0}^{\infty} \frac{\log x}{\left(1+x^{2}\right)^{2}} d x+\int_{0}^{\infty} \frac{\log x e^{i \pi}}{\left(1+x^{2} e^{i 2 \pi}\right)^{2}} d x=2 \pi i\left[- \frac{1}{4i} \left(1-\frac{i \pi}{2}\right)\right]\\ =-\frac{\pi}{2}\left(1-i \frac{\pi}{2}\right)
काल्पनिक और वास्तविक भागों की तुलना करने पर-

2 \int_{0}^{\infty} \frac{\log x}{\left(1+x^{2}\right)^{2}} d x=-\frac{\pi}{2} \\ \Rightarrow \int_{0}^{\infty} \frac{\log x}{\left(1+x^{2}\right)^{2}} d x=-\frac{\pi}{4}
Example-3.\int_{0}^{\infty} \sin x^{2} d x=\int_{0}^{\infty} \cos x^{2} d x=\frac{1}{2} \sqrt{\left(\frac{\pi}{2}\right)}

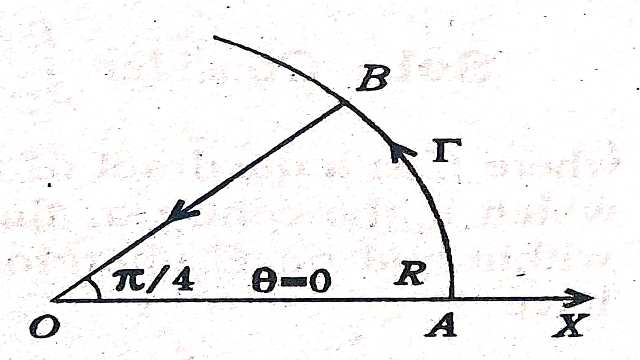
Solution:-\int_{0}^{\infty} \sin x^{2} d x=\int_{0}^{\infty} \cos x^{2} d x=\frac{1}{2} \sqrt{\left(\frac{\pi}{2}\right)} \\ \int_{C} f(z)=\int_{c} e^{-z^{2}} d z

जहां C चित्र में दर्शाए अनुसार परिरेखा है।

अतः कोशी अवशेष प्रमेय से-

\int_{C} f(z) d z=\int_{O A} f(z) d z+\int_{A B} f(z) d z+\int_{B O} f(z) d z=0 \\ \Rightarrow \int_{0}^{R} e^{-x^{2}} d x+\int_{\Gamma} e^{-z^{2}} d z+\int_{R}^{0} \cdot e^{-r^{2}} e^{i \pi / 2} e^{i \pi / 4} dr=0 \cdots (1)
अब \left|\int_{\Gamma} e^{-z^{2}} d z\right| =\left|\int_{0}^{\pi / 4} e^{-R^{2} e^{i 2 \theta}} i R e^{i \theta}\right| d \theta \\ \leq \int_{0}^{\pi / 4} R \exp \left(-R^{2} \cos 2 \theta\right) d \theta \\ \leq \frac{1}{2} \int_{0}^{\pi / 2} R e^{-R^{2} \sin \phi} d \phi [2 \theta=\frac{\pi}{2}-\phi रखने पर ]

\leq \frac{1}{2} \int_{0}^{\pi / 2} R e^{-(2 \phi \pi) R^{2}} d \phi
(जोर्डन असमिका से)
\leq \frac{\pi}{4 R}\left(1-e^{-R^{2}}\right) \rightarrow 0 जब R \rightarrow \infty
अब R \rightarrow \infty ; समीकरण (1) से-

\int_{0}^{\infty} e^{-x^{2}} d x-\int_{0}^{\infty} e^{i r^{2}}\left(\frac{1}{\sqrt{2}}+i \frac{1}{\sqrt{2}}\right) dr=0 \\ \int_{0}^{\infty}\left(\cos x^{2}-i \sin x^{2}\right)\left(\frac{1}{2}+\frac{i}{\sqrt{2}}\right) d x=\int_{0}^{\infty} e^{-x^{2}} d x \\ =\frac{\sqrt{\pi}}{2}
काल्पनिक और वास्तविक भागों की तुलना करने पर-

\int_{0}^{\infty}\left(\cos x^{2}+\sin x^{2}\right) d x=\sqrt{\frac{\pi}{2}}
तथा \int_{0}^{\infty}\left(\cos x^{2}-\sin x^{2}\right) d x=0
दोनों को जोड़ने पर-

\int_{0}^{\infty} \cos x^{2} d x=\frac{1}{2} \sqrt{\left(\frac{\pi}{2}\right)}
यह मान ऊपर किसी एक समीकरण में रखने पर-

\int_{0}^{\infty} \sin x^{2} d x=\frac{1}{2} \sqrt{\left(\frac{\pi}{2}\right)}
अतः \int_{0}^{\infty} \sin x^{2} d x=\int_{0}^{\infty} \cos x^{2} d x=\frac{1}{2} \sqrt{\left(\frac{\pi}{2}\right)}
Example-4. \int_{0}^{\infty} \frac{x \sin x d x}{1+a^{2}-2 a \cos x}=\left\{\begin{array}{l} \frac{\pi}{a} \log (1+a) \text{ यदि  } (i f) \quad 0<a<1 \\ \frac{\pi}{a} \log \frac{(1+a)}{a} \text{ यदि  } (if) \quad a>1 \end{array}\right.
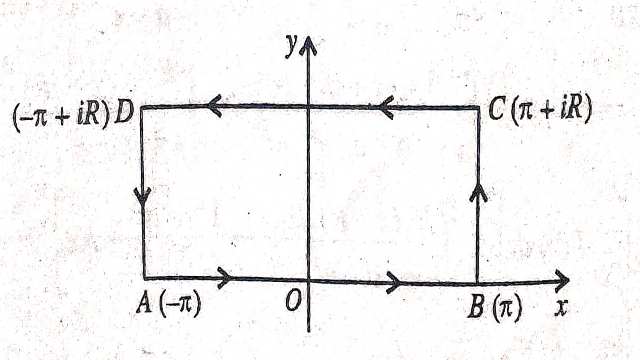
Solution–\int_{0}^{\infty} \frac{x \sin x d x}{1+a^{2}-2 a \cos x}=\left\{\begin{array}{l} \frac{\pi}{a} \log (1+a) \text{ यदि  } (i f) \quad 0<a<1 \\ \frac{\pi}{a} \log \frac{(1+a)}{a} \text{ यदि  } (if) \quad a>1 \end{array}\right. \\ \int_{c} \frac{z}{a-e^{-i z}} d z=\int_{c} f(z) d z
जहां C,एक ABCD आयत है जिसके शीर्ष -\pi, \pi, \pi+i R,-\pi+i R हैं।

f(z) के अनन्तक के लिए-

a-e^{-i z}=0 \Rightarrow e^{-i z}=a \\ \Rightarrow e^{-i z}=e^{\log a} \\ \Rightarrow e^{-i z}=e^{\log a} \cdot e^{2 n \pi i} \\ \Rightarrow e^{-i z}=e^{2 n \pi i+\log a} \\ \Rightarrow -i z =2 n \pi i+\log a \\ \Rightarrow z=-2 n \pi +i \log a
जहां n=0,\pm 1,\pm 2, \ldots
स्थिति-I.जब a>1
f(z) का सरल अनन्तक है z=i \log a जो C के अन्दर है।
z=i \log a पर अवशेष=\lim _{z \rightarrow i \log a} \frac{\phi(z)}{\psi^{\prime}(z)} \\ =\lim _{z \rightarrow i \log a} \frac{z}{i e^{-i z}} \\ =\frac{i \log a}{i e^{\log a}} \\ =\frac{\log a}{a}
कोशी अवशेष प्रमेय से-

\int_{c} f(z) d z =2 \pi i अवशेष (z=i \log a) \\ =2 \pi i \cdot \frac{\log a}{a} \\ =\frac{2 \pi i}{a} \log a \\ \left\{ \int_{A B} + \int_{B C}+\int_{C D}+\int_{D A}\right\} f(z) d z=\frac{2 \pi i}{a} \log a....(1) \\ \int_{A B} f(z) d z =\int_{-\pi}^{\pi} f(x) d x \\ =\int_{- \pi}^{\pi} \frac{x d x}{a-e^{-i x}} \\ =\int_{-\pi}^{0} \frac{x d x}{a-e^{-i x}}+\int_{0}^{\pi} \frac{x d x}{a-e^{-i x}} \\ =\int_{\pi}^{0} \frac{-x(-d x)}{a-e^{i x}}+\int_{0}^{\pi} \frac{x d x}{a-e^{-i x}}
(प्रथम समाकल में x की जगह -x परिवर्तित करके रखने पर)

=\int_{0}^{\pi} x\left[\frac{1}{a-e^{-i x}}-\frac{1}{a-e^{i x}}\right] d x \\ \int_{A B} f(z) d z =\int_{0}^{\pi} \frac{x(-2 i \sin x) d x}{a^{2}+1-2 a \cos x} \cdots(2) \\ \int_{B C} f(z) d z =\int_{0}^{R} f(\pi+i y) i d y=\int_{0}^{R} \frac{(\pi+i y) \cdot i d y}{a-e^{i(n+i y)}} \\ =\int_{0}^{R} \frac{i \pi d y}{a+e^{y}}-\int_{0}^{R} \frac{y d y}{a+e^{y}}[\because e{-i \pi} =-1]
परन्तु \int_{0}^{R} \frac{1}{a+e^{y}} d y =-\frac{1}{a} \int_{0}^{R} \frac{-a e^{-y} d y}{a e^{-y}+1} \\ =-\frac{1}{a}\left[\log \left(1+a e^{-y}\right)\right]_{0}^{R} \\ =\frac{1}{a}\left[\log (1+a)-\log \left(1+\frac{a}{e^{R}}\right)\right] \\ \int_{0}^ {\infty} \frac{d y}{a+e^{y}} =\frac{1}{a} \log (1+a)....(3) \\ \lim _{R \rightarrow \infty} \int_{B C} f(z) d z=\frac{i \pi}{a} \log (1+a)-\int_{0}^{\infty} \frac{x d x}{a+e^{x}} \cdots(4) \\ \int_{C D} f(z) d z=\int_{\pi}^{-\pi} f(x+i R) d x \\ =\int_{\pi}^{-\pi} \frac{(x+i R) d x}{a-e^{-i(x+i R)}} \\ =\int_{\pi}^{-\pi} \frac{(x+i R) d x}{a-e^{-i x} e^{R}} \\ =-\int_{-\pi}^{\pi} \frac{(x+i R) d x}{a-i x \cdot e^{R}} \\ |\int_{CD} f(z) \cdot d z| \leq \int_{-\pi}^{\pi} \frac{(x+R) d x}{a-e^{R}} \\ \leq \frac{1}{a-e^{R}}\left[\frac{x^{2}}{2}+R x\right]_{-\pi}^{\pi}=0
यदि R \rightarrow \infty \\ \lim _{R \rightarrow \infty} \int_{C D} f(z) d z=0 \\ \int_{D A} f(z) d z =\int_{R}^{0} f(-\pi + i y) \cdot i d y \\ =-\int_{R}^{0} \frac{(-\pi+i y) i d y}{a-e^{-i(-\pi-iy)}} \\ =-\int_{0}^{R} \frac{(-i \pi-y) }{a+e^{y}} dy \\ \lim _{R \rightarrow \infty} \int_{DA} f(z) d z =i \pi \int_{0}^{\infty} \frac{d y}{a+e^{y}}+\int_{0}^{\infty} \frac{y d y}{a+e^{y}} \\ =\frac{i \pi}{a} \log (1+a)+\int_{0}^{\infty} \frac{x d x}{a+e^{x}} [(3) से]……..(6)
समीकरण (1) में जब R \rightarrow \infty तो (2),(4),(5) और (6) से-

-2 i \int_{0}^{\pi} \frac{x \sin x d x}{a^{2}+1-2 a \cos x}+\frac{2 \pi i}{a} \log (1+a)=\frac{2 \pi i \log a}{a} \cdots (7) \\ \int_{0}^{\pi} \frac{x \sin x d x}{a^{2}+1-2 a \cos x}=\frac{\pi}{a} \log \left(\frac{1+a}{a}\right) \cdots(8)
स्थिति-II जब 0<a<1

\left\{\int_{A B} + \int_{A C}+\int_{C D}+\int_{D A}\right\} f(z) d z=0

अतः समीकरण (7) से-

-2 i \int_{0}^{\pi} \frac{x \sin x d x}{a^{2}+1-2 a \cos x}+\frac{2 \pi i}{a} \log (1+a)=0 \\ \int_{0}^{\pi} \frac{x \sin x d x}{a^{2}+1-2 a \cos x}=\frac{\pi}{a} \log (1+a)....(9)

(8) तथा (9) से

\int_{0}^{\pi} \frac{x \sin x d x}{1+a^{2}-2 a \cos x}=\left[\begin{array}{l} \frac{\pi}{a} \log (1+a) \cdot (i f) \cdot 0<a<1 \\ \frac{\pi}{a} \log \left(\frac{1+a}{a}\right) (i f) \cdot a>1 \end{array}\right.
Example-5.\int_{-\infty}^{\infty} \frac{e^{a x}}{e^{x}+1} d x=\int_{0}^{\infty} \frac{t^{a-1}}{1+t} d t=\pi \operatorname{cosec} \pi a(0<a<1)
Solution–\int_{-\infty}^{\infty} \frac{e^{a x}}{e^{x}+1} d x=\int_{0}^{\infty} \frac{t^{a-1}}{1+t} d t=\pi cosec \pi a

माना f(z)=\frac{e^{a z}}{e^{z}+1} तथा 0<a<1
अतः f(z) के अनन्तक के लिए

e^{z}+1=0 \Rightarrow e^{z}=-1 \\ \Rightarrow e^{z}=e^{(2 n+1) \pi i} \\ \Rightarrow z=(2 n+1) \pi i
जहां n=0,\pm 1,\pm 2, \ldots
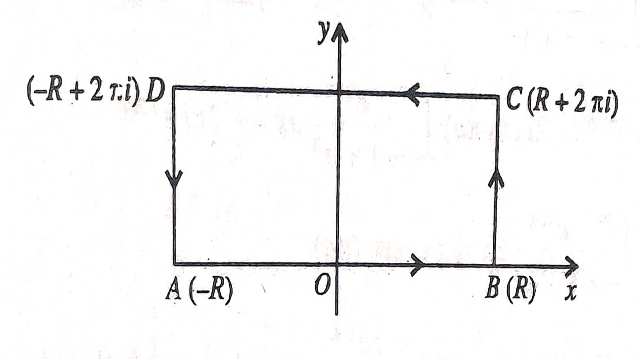
\int_{c} f(z) d z के समाकलन पर विचार करें जहां C,ABCD एक आयत है।
C के अन्दर केवल z=\pi i अनन्तक है-
z=\pi i  पर अवशेष=\lim _{z \rightarrow \pi i} \frac{\phi(z)}{\psi^{\prime}(z)}
[जहां f(z)=\frac{\phi(z)}{\psi(z)}] 

=\lim _{z \rightarrow \pi i} \frac{e^{a z}}{e^{z}} \\ =\frac{e^{i \pi a} }{e^{i \pi}} \\ =-e^{i \pi a}
कोशी अवशेष प्रमेय से-
\int_{c} f(z) d z =2 \pi i अवशेष (z=\pi i पर)

=2 \pi i \left(-e^{i \pi a}\right) \\ \left\{\int_{A B}+\int_{B C}+\int_{C D}+\int_{D A}\right\} f(z) d z=-2 \pi i e^{i \pi a}......(1) \\ \Rightarrow \int_{A B} f(z) d z=\int_{A B} f(x) d x=\int_{-R}^{R} \frac{e^{a x}}{e^{x}+1} d x.....(2) \\ \int_{B C} f(z) d z =\int_{B C} f(R+i y) i d y \\ =\int_{0}^{2 \pi}  \frac{e^{a(R+i y)}}{1+ e^{R+i y}} i d y \\ =\int_{0}^{2 \pi} \frac{e^{a R} \cdot e^{i a y}}{e^{R} \cdot e^{i y}+1} i d y \\ \left|\int_{BC} f(z) d z\right| \leq \frac{e^{a R}}{e^{R}-1} \int_{0}^{2 \pi} d y \\ \left[\because \frac{1}{\left|z_{1}+z_{2}\right|}\right. \left.\leq \frac{1}{\left|z_{1}\right|-\left|z_{2}\right| } \quad, \left|e^{i a y}\right|=1=| i| \right] \\ \leq \frac{2 \pi e^{a R}}{e^{R}-1} \\ \leq 2 \pi \cdot \frac{1}{e^{R(1-a)}-e^{-a R}} \rightarrow 0
जब R \rightarrow \infty   [\because 1-a>0,-a<0]

\therefore \lim _{R \rightarrow \infty} \int_{B C} f(z) d z=0 \quad \cdots \cdot(3)
इसी तरह यह दर्शाया जा सकता है कि

\lim _{R \rightarrow \infty} \int_{D A} f(z) d z=0 \\ \int_{C D} f(z) d z =\int_{R}^{-R} f(x+2 \pi i) d x \\ =\int_{R}^{-R} \frac{e^{a(x+2 \pi i)} d x}{e^{x+2 \pi i}+1} \\ \Rightarrow \int_{C D} f(z) d z=-\int_{-R}^{R} \frac{e^{2 \pi i a} \cdot e^{a x}}{e^{x}+1} d x \cdots(5)
समीकरण (1) में R \rightarrow \infty तथा समीकरण (2),(3),(4) तथा (5) से-

\int_{-\infty}^{\infty} \frac{e^{a x}}{e^{x}+1}\left(1-e^{2 \pi i a}\right) d x=-2 \pi i e^{i \pi a} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{a x}}{e^{x}+1} e^{i \pi a} \left(e^{-i \pi a}-e^{i \pi a}\right) d x=-2 \pi i e^{i \pi a} \\ \Rightarrow e^{i \pi a} (-2 i \sin \pi a) \int_{-\infty}^{\infty} \frac{e^{a x}}{1+e^{x}} d x=-2 \pi i e^{i \pi a} \\ \Rightarrow \int_{-\infty}^{\infty} \frac{e^{a x}}{1+e^{x}}=\pi \operatorname{cosec}(\pi a)
Example-6.\int_{0}^{\infty} \frac{\sinh a x}{\sinh \pi x} d x=\frac{1}{2} \tan (\frac{a}{2}),(-\pi<a<\pi)
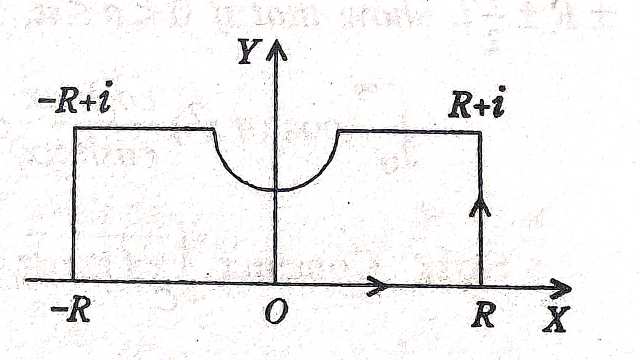
Solution-\int_{c} \frac{\sinh a z}{\sin h \pi z} d z=\int_{c} f(z) d z

जहां C एक आयत है जिसके शीर्ष R,R+i,-R+i,-R तथा अनन्तक z=i  इस पर हैं।अनन्तक के लिए-

\sinh \pi z=0 \Rightarrow e^{\pi z}-e^{-\pi z}=0 \\ \Rightarrow e^{2 \pi z}=1 \Rightarrow e^{2 \pi z}=e^{2 n \pi i} \\ z=n i, n=0,\pm 1,\pm 2, \ldots \ldots
इस प्रकार z=\pm i, \pm 2 i \ldots ,f(z) के साधारण अनन्तक हैं।अतः कोशी अवशेष प्रमेय से-

\int_{c} f(z) d z=\int_{-R}^{R} f(x) d x- \int_{0}^{1} f(R+i y) i d y+\int_{R}^{\rho} f(x+i) d x+ \int_{\gamma} f(z) d z+\int_{-\rho}^{-R} f(x+i) d x+\int_{1}^{0} f(-R+i y)id y=0 \\ \int_{0}^{1} f(R+i y) i d y =\int_{0}^{1} \frac{\sinh a(R+i y) i d y}{\sinh \pi(R+i y)} \\ =\int_{0}^{1} \frac{e^{a R}(\cos a y+i \sin a y)}{e^{\pi R}(\cos \pi y+i \sin \pi y)} i d y \rightarrow 0 जब R \rightarrow \infty \\  \lim _{z \rightarrow i}(z-i) f(z) =\lim _{z \rightarrow i}(z-i) \frac{\sinh a z}{\sinh \pi z} \\ =\frac{\sinh a i}{\pi \cosh \pi i}=\frac{-i}{\pi} \sin a \\ \lim _{\rho \rightarrow 0} \int_{\gamma} f(z) d z =i(0-\pi)\left(-\frac{\sin a}{\pi}\right)=-\sin a
जब R \rightarrow \infty , \rho \rightarrow 0 अतः समीकरण (1) से-

\int_{-\infty}^{\infty} f(x) d x+\int_{\infty}^{0} f(x+i) d x-\sin a+\int_{0}^{-\infty} f(x+i) d x=0 \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\sinh a x}{\sinh \pi x} d x-\int_{-\infty}^{\infty} \frac{\sinh a(x+i)}{\sin \pi (x+i)} d x=\sin a \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\sinh a x+\sinh a(x+i)}{\sinh \pi x}=\sin a[\because \sinh \pi (x+i)=-\sinh \pi x] \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\sinh a x+\sinh ax \cos a+i \cos a x \sin a}{\sinh \pi x} d x=\sin a
वास्तविक और काल्पनिक भागों की तुलना करने पर-

\int_{-\infty}^{\infty} \frac{\sin a x(1+\cos a)}{\sinh \pi x} d x=\sin a \\ \Rightarrow \int_{-\infty}^{\infty} \frac{\sinh a x}{\sinh \pi x} d x=\frac{\sin a}{1+\cos a} \\ \Rightarrow \int_{0}^{\infty} \frac{\sinh a x}{\sinh \pi x} d x=\frac{1}{2} \tan \left(\frac{a}{2}\right)
उपर्युक्त उदाहरणों के द्वारा परिरेखा समाकलन,कन्टूर समाकलन (Contour Integration) को समझ सकते हैं।

3.परिरेखा समाकलन की समस्याएं,कन्टूर समाकलन की समस्याएं (Contour Integration Problems)-

सिद्ध कीजिए कि (Prove that):

(1.) \int_{0}^{\infty} \frac{x}{\sin x} d x=\frac{\pi^{2}}{4} \\ (2) \int_{0}^{\infty} \frac{\log x}{1+x^{2}} d x=0 \\ (3) \int_{0}^{\infty} \frac{\log x}{(x+a)^{2}+b^{2}} d x=\frac{1}{2 b} \log \left(a^{2}+b^{2}\right) \tan^{-1} (\frac{b}{a}) \\ (4) \int_{0}^{\infty} \frac{(\log x)^{2}}{1+x^{2}} d x=\frac{\pi^{3}}{8}
उपर्युक्त सवालों को हल करने पर परिरेखा समाकलन,कन्टूर समाकलन (Contour Integration) को ठीक से समझ सकते हैं।

4.कन्टूर समाकल से क्या मतलब है? (What is meant by contour integral?)-

कन्टूर समाकलन सम्मिश्र समतल में दिए गए कन्टूर के आसपास कन्टूर समाकल के मूल्यों की गणना करने की प्रक्रिया है।होलोमोर्फिक फलनों की वास्तव में आश्चर्यजनक गुणधर्मों के परिणामस्वरूप, कन्टूर के अंदर सम्मिश्र अवशेषों के मूल्यों को संक्षेप में आसानी से इस तरह के समाकल की गणना की जा सकती है।

5.आप सम्मिश्र कन्टूर समाकलन कैसे हल करते हैं? (How do you solve complex contour integration?),कन्टूर समाकल को कैसे हल करें? (how to solve contour integrals?)-

सम्मिश्र विश्लेषण के गणितीय क्षेत्र में, कन्टूर समाकलन सम्मिश्र समाकल में पथों के साथ कुछ इंटीग्रल का मूल्यांकन करने की एक विधि है।कन्टूर इंटीग्रल्स के लिए एक उपयोग वास्तविक लाइन के साथ इंटीग्रल का मूल्यांकन है जो केवल वास्तविक चर विधियों का उपयोग करके आसानी से नहीं पाया जाता है।
कन्टूर समाकल एक शक्तिशाली तकनीक है, जो सम्मिश्र विश्लेषण पर आधारित है, जो हमें कुछ ऐसे इंटीग्रल्स को हल करने की अनुमति देती है जो अन्यथा मुश्किल या हल करना असंभव है।
कन्टूर समाकलन सम्मिश्र समतल में दिए गए कन्टूर के आसपास कन्टूर समाकल के मूल्यों की गणना करने की प्रक्रिया है।

6.आप समाकलन के लिए कन्टूर को कैसे चुनते हैं? (How do you choose contour for integration?)-

एक साधारण कन्टूर के लिए बंद कन्टूर को एक या एक से अधिक अनन्तक से जोड़ना होगा अन्यथा समाकल शून्य है। यदि समतल में एक या एक से अधिक "कटौती" होती है, तो स्थिति अधिक सम्मिश्र है और मामले के आधार पर मामले को संभालने की आवश्यकता है।(एक कट एक फंक्शन द्वारा उत्पन्न होता है जैसे कि वर्गमूल या लघुगणक।)

7.इंजीनियरिंग में कन्टूर समाकलन का अनुप्रयोग (Application of contour integration in engineering)-

कन्टूर समाकलन एन्ट्रापी अध्ययन में प्रकट होता है और अवशेषों के सिद्धांत की रीढ़ है जो बदले में, कुछ अनुचित इंटीग्रल्स का मूल्यांकन करने के लिए कई प्रसिद्ध अनुप्रयोगों का पता लगाता है, और फ्यूरियर, लाप्लास और जेड ट्रांसफॉर्म की गणना करने के लिए एक फोर्टियरी, उन सभी में बुनियादी उपकरण परिचालन कैलकुलस और सिग्नल विश्लेषण।

Also Read This Article:-Argument Principle and Rouche Theorem

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here