Constrained Motions in Dynamics
1.गति विज्ञान में प्रतिबन्धित गति (Constrained Motions in Dynamics),प्रतिबन्धित गति (Constrained Motions):
गति विज्ञान में प्रतिबन्धित गति (Constrained Motions in Dynamics) पर आधारित कुछ सवालों का हल इससे पूर्व आर्टिकल में कर चुके हैं।इस आर्टिकल में कुछ ओर सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Motion in Horizontal Elastic String
2.गति विज्ञान में प्रतिबन्धित गति के साधित उदाहरण (Constrained Motions in Dynamics Solved Examples):
Example:2.कोई कण एक स्थिर गोले के अन्तःतल के साथ गोले के सबसे नीचे के बिन्दु से उतने वेग से प्रक्षिप्त किया जाता है जितना वेग उस कण को उर्ध्वाधर व्यास पर स्वतन्त्र रूप से गिरने पर होगा।सिद्ध कीजिए कि कण गोले को छोड़ देगा तथा तत्पश्चात प्रक्षेप बिन्दु के ऊपर से व्यास के \frac{25}{32} दूरी की ऊँचाई से गुजरेगा।
(A particle is projected,along the inside of a smooth fixed sphere from its lowest point, with a velocity equal to that due to falling freely down the vertical diameter of the sphere.Show that the particle will leave the sphere and afterwards pass vertically over the point of projection at a distance equal to \frac{25}{32} of the diameter.)
Solution:माना कण सबसे नीचे बिन्दु A से प्रक्षिप्त किया जाता है।
प्रक्षेप वेग u=\sqrt{(2 g \cdot 2 a)}=\sqrt{4 a g}
गति का समीकरण
m\left(\frac{d^2 s}{d t^2}\right)=-m g \sin \theta \cdots(1) \\ \Rightarrow m\left(\frac{v^2}{a}\right)=R-m g \cos \theta \cdots(2)
तथा s=a \theta \cdots(3)
(3) का (1) में प्रयोग करने पर:
a\left(\frac{d^2 \theta}{d t^2}\right)=-g \sin \theta
समाकलन करने पर:
v^2=\left(a \frac{d \theta}{d t}\right)^2=2 a g \cos \theta+A
सबसे नीचे के बिन्दु A पर , \theta=0 तथा v=\sqrt{4 a g} \\ \therefore A=4 a g-2 a g=2 a g \\ \therefore V^2=2 a g \cos \theta+2 a g \cdots(4)
(4) का (2) में प्रयोग करने पर:
R=\left(\frac{m}{a}\right)(a g \cos \theta+v^2) \\ \Rightarrow R=\left(\frac{m}{a}\right)(3 a g \cos \theta+2 a g) \cdots(5) जहाँ 2 a g<u^2<5 a g
इसलिए कण गोले को \theta_{1} कोण पर छोड़ देगा
जहाँ \frac{\pi}{2}<\theta_1<\pi
कण गोले को Q बिन्दु पर छोड़ देगा जहाँ \theta=\theta_1
समीकरण (5) से:
R=0=\frac{m}{a}\left(3 a g \cos \theta_1+2 a g\right) \\ \Rightarrow \cos \theta_1=\left(-\frac{2}{3}\right)
यदि Q पर कण की गति है तब (4) से:
V_1^2=2 a g \cos \theta_1+2 a g \\ =2 \operatorname{ag}(\cos \theta+1) \\ =2 a g\left(-\frac{2}{3}+1\right) \\ \Rightarrow v_1^2=\frac{2}{3} a g
यदि \angle BOQ=\alpha तब \alpha=\pi-\theta_1 \\ \therefore \cos \alpha=\cos \left(\pi-\theta_1\right)=-\cos \theta_1=\frac{2}{3}
अतः कण गोले को Q बिन्दु पर \alpha=\cos ^{-1}\left(\frac{2}{3}\right) कोण पर वेग v_1=\sqrt{\left(\frac{2}{3} a g\right)} से छोड़ देगा और तब वह परवलयिक पथ का अनुसरण करेगा
कण के परवलयिक पथ का समीकरण गोले के Q बिन्दु पर QX और QY के सापेक्ष होगी
y=x \tan \alpha-\frac{g x^2}{2 v_1^2 \cos ^2 \alpha} \\ \Rightarrow y=x \cdot \frac{\sqrt{5}}{2}-\frac{g x^2}{2 \times \frac{2}{3} a g \times \frac{4}{9}} \\ \left[\because \cos \alpha=\frac{2}{3}, \sin \alpha= \sqrt{\left(1-\cos ^2 \alpha\right)}=\frac{\sqrt{5}}{3}\right] \\ \tan \alpha=\frac{\sqrt{5}}{2} \\ \Rightarrow y=\frac{\sqrt{5}}{2} x-\frac{27}{16} x^2
यदि कण प्रक्षेप बिन्दु A के ऊपर लम्बवत बिन्दु M से गुजरता है,तब M का x-निर्देशांक
x=Q L=a \sin \alpha=a \sqrt{\left(\frac{5}{3}\right)}
माना M पर y-निर्देशांक है।
बिन्दु M(a \frac{\sqrt{5}}{3}, y) परवलयिक पथ पर पड़ता है अतः (5) से
y_1=\frac{\sqrt{5}}{2} \cdot \frac{\sqrt{5}}{3} a-\frac{27}{16} a \cdot \frac{5 a^2}{9} \\ y_1=\frac{5 a}{6}-\frac{15 a}{16}=-\frac{5 a}{48}
M का y-निर्देशांक ऋणात्मक है अतः M बिन्दु x-अक्ष QX के नीचे है
अभीष्ट ऊँचाई=AM=AO+OL+y
=a+a \cos \alpha+y, \\=a+\frac{2}{3} a-\frac{5 a}{48} \\ =\frac{25 a}{16} \\ =\frac{25}{32} \cdot(2 a)
अतः अभीष्ट ऊँचाई व्यास \frac{25}{32} का होगी।
Example:3.एक कण किसी a अर्द्धव्यास वाले चिकने वृत्त के अन्दर फेंका जाता है।उसकी सबसे नीचे के बिन्दु पर गति u है।सिद्ध कीजिए कि वह वृत्त की सबसे ऊँचे बिन्दु पर पहुँचने से पहले छोड़ देगा और एक परवलय तय करेगा जिसका नाभिलम्ब \frac{2\left(u^2-2 g a\right)^3}{27 g^3 a^2} (यदि 2 g a<u^2<5g a) है।
(A particle is projected along the innerside of s smooth circle of radius a,the velocity at the lowest point being u.Show that if 2ga<u^2<5 g a , the particle will leave the circle before arriving at the heighest point and will describe a parabola of latus rectum \frac{2\left(u^2-2 g a\right)^3}{27 g^3 a^2} .)
Solution:वेग v तथा प्रतिक्रिया R समय t पर दिया जाता है:
v^2=u^2-2 a g+2 a g \cos \theta \cdots(1)
तथा R=\frac{m}{a}\left(u^2-2 a g+3 a g \cos \theta\right) \cdots(2)
Q बिन्दु पर कण वृत्त छोड़ देगा जहाँ \angle AOQ=\theta
तब (2) से:
0=\frac{m}{a}\left(u^2-2 a g+3 a g \cos \theta_1\right) \\ \Rightarrow \cos \theta_1=-\frac{u^2-2ag}{3ag}
जब 2ag<u^2<5 a g,इसलिए ऋणात्मक है और इसका निरपेक्ष मान <1 है।इसलिए \theta_1 वास्तविक है और \frac{1}{2} \pi<\theta_1<\pi
इस प्रकार कण उच्चतम बिन्दु पर वृत्त को छोड़ देगा।यदि Q बिन्दु वेग v_{1} है तब v=v_{1} जब \theta=0 ,समीकरण (1) सेः
v_1^2=u^2-2 a g+2 a g \cos \theta_1 \\ =\left(u^2-2 a g\right)-2 a g\left(\frac{u^2-2 a g}{3 a g}\right) \\ =\left(u^2-2 a g\right)\left(1-\frac{2}{3}\right) \\ =\frac{1}{3}\left(a^2-2 a g\right)
यदि \angle BOQ=\alpha तब \alpha=\pi-\theta_1 \\ \therefore \cos \alpha=\cos \left(\pi-\theta_1\right)=-\cos \theta_1 \\ =\frac{u^2-2 a g}{3 a g}
इस प्रकार कण बिन्दु Q पर वेग से वृत्त को छोड़ देगा और क्षैतिज के साथ कोण बनाएगा तथा यह परवलयिक पथ पर गमन करेगा
परवलय का नाभिलम्ब=\frac{2}{g} v_1^2 \cos ^2 \alpha \\ =\frac{2}{g} \cdot \frac{1}{3}\left(u^2-2 a g\right)\left(\frac{u^2-2 a g}{3 a g}\right)^2 \\ =\frac{2\left(u^2-2 a g\right)^3}{27 a^2 g^3}
Example:6.एक कण 1 मी. लम्बी एक अप्रत्यास्थ डोरी के सिरे से बँधा है।उसे ऐसे प्रारम्भिक क्षैतिज वेग से चलाया जाता है कि डोरी ढीली पड़ जाती है,जब कण निम्नतम बिन्दु से मी. ऊँचा है।सिद्ध करो कि वह \frac{5}{27} मी. ओर ऊँचा जायेगा।
(A particle is hanging from a fixed point by a light inelastic cord 1m long and has started moving with an initial horizontal velocity such that the cord slackens when the particle is above the lowest point.Show that it will rise further through \frac{5}{27} m)
Solution:दिया हुआ है कि निम्नतम बिन्दु A से कण को 2 \sqrt{g} वेग से प्रक्षिप्त किया,तो यदि कण किसी समय t पर P बिन्दु पर है तथा \angle POA=\theta जहाँ O स्थिर बिन्दु है तो ऊर्जा समीकरण से
तथा अभिलम्ब दिशा में समीकरण होगा:
\frac{m v^2}{l}=T-m g \cos \theta \cdots(2)
(1) और (2) में v^2 का मान रखने पर:
T=\frac{m}{l}[4 g-2 g(1-\cos \theta)]+m g \cos \theta \\ =m g(2+3 \cos \theta)
जब डोरी ढीली होगी तब T=0,माना \theta=\alpha,तब T=0
\therefore \quad 2+3 \cos \alpha=0, \Rightarrow \cos \alpha=-\frac{2}{3}
डोरी ढीली होने के समय कण की स्थिर बिन्दु O से ऊँचाई
=1 \cos (\pi-\alpha) \\ =-\cos \alpha=\frac{2}{3}
अतः प्रक्षेप बिन्दु से ऊँचाई=\frac{2}{3}+1=\frac{5}{3} मी.
तथा उस बिन्दु पर वेग
\text{(वेग)}^{2}=V^2=4 g-2 g(1-\cos \alpha) \\ =2 g-2 g \times \frac{2}{3}=\frac{2 g}{3}
वृत्तीय पथ छोड़ने के पश्चात कण की इस बिन्दु से ऊँचाई
\frac{\text{(उर्ध्वाधर वेग)}^2}{2g} \\=\frac{V^2 \sin ^2 \alpha}{2 g} \\ =\frac{\left(\frac{2 g}{3}\right)}{2 g}\left(1-\cos ^2 \alpha\right) \\ =\frac{1}{3}\left(1-\frac{4}{9}\right) \\ =\frac{5}{27}
Example:12.एक भारी कण किसी बिन्दु से भारहीन a लम्बाई की अवितान्य रस्सी द्वारा उर्ध्वाधर दिशा में लटक रहा है।वह \sqrt{(2 g h)} वेग से क्षैतिज दिशा में प्रक्षिप्त किया जाता है।यदि \frac{5}{2}a >h >a सिद्ध कीजिए कि वृत्तीय गति उस समय समाप्त हो जाती है जब वह \frac{1}{3}(a+2 h) ऊँचाई तक पहुँच जाता है।साथ ही यह भी सिद्ध कीजिए कि कण प्रक्षेप बिन्दु से अधिकतम ऊँचाई \frac{(4 a-h)(a+2 b)^2}{27 a^2} तक सम्पूर्ण गति में पहुँच जाता है।
(A heavy particle hangs by an in extensible string of length a form a fixed point and is then projected horizontally with a velocity \sqrt{(2 g h)}.If \frac{5}{2}a >h >a , prove that the circular motion ceases when the particle has reached the height \frac{1}{3}(a+2 h).Prove also that the greatest height ever reached by the particle above the point of projection is \frac{(4 a-h)(a+2 b)^2}{27 a^2})
Solution:माना कि एक m द्रव्यमान का भारी कण a लम्बाई की डोरी जिसका दूसरा सिरा O पर स्थिर है।कण उर्ध्वाधर वेग u=\sqrt{(2 g h)} , A बिन्दु से क्षैतिज से प्रक्षिप्त किया जाता है।यदि किसी समय t पर कण की स्थिति P इस प्रकार है कि \angle AOP=\theta तथा चाप AP=s.
गति का स्पर्श रेखीय तथा अभिलाम्बिक समीकरण है:
m \frac{d^2 s}{d t^2}=-m g \sin \theta \cdots(1)
तथा \frac{m v^2}{a}=T-m g \cos \theta \cdots(2) \\ s=a \theta \cdots(3)
(3) का (1) में प्रयोग करने पर:
a \frac{d^2 \theta}{dt^2}=-g \sin \theta
दोनों पक्षों को 2 a \frac{d \theta}{d t} से गुणा करने तथा समाकलन करने पर:
v^2=\left(a \frac{d \theta}{d t}\right)^2=2 a g \cos \theta+A
प्रारम्भ में बिन्दु A पर, \theta=0 तथा v=u=\sqrt{(2 g h)} \\ \therefore A=2 g h-2 a g \\ \therefore v^2=2 a g \cos \theta+2 g h-2 a g \cdots(4)
समीकरण (2) तथा (4) से:
T=\frac{m}{a}\left(v^2+a g \cos \theta\right) \\ \Rightarrow T=\frac{m}{a}(3 a g \cos \theta+2 g h-2 a g)
यदि कण वृत्तीय पथ Q पर छोड़ देता है
जहाँ \theta=\theta_{1},तब t=0 व \theta=\theta_1 \\ \therefore 0=\frac{m}{a}\left(3 a g \cos \theta_1+2 g h-2 a g\right) \\ \Rightarrow \cos \theta_1=-\frac{2 h-2 a}{3 a}
जब \frac{5}{2}a>h>a अर्थात् 5a>2 h>2 a, इसलिए \cos \theta_1 ऋणात्मक तथा इसका निरपेक्ष मान<1.अतः \theta_1 वास्तविक होगा तथा \frac{1}{2} \pi<\theta_1<\pi
कण Q पर वृत्तीय पथ को छोड़ उच्चतम ऊँचाई पर पहुँचने से पहले
A के ऊपर उच्चतम ऊँचाई Q पर
=AL=AO+OL=a+a \cos (\pi-\theta_{1}) \\ =a-a \cos \theta_1 \\ =a+a \cdot\left(\frac{2 h-2 a}{3 a}\right) \\ =\frac{1}{3}(a+2 h)
कण प्रक्षेप बिन्दु A के ऊपर \frac{1}{3}(a+2 h) ऊँचाई पर वृत्तीय पथ छोड़ देगा।
यदि Q पर कण का वेग हो तो समीकरण (4) से:
V_1^2=2 a g \cos \theta_1+2 g h-2 a g \\=-2 a g \cdot \frac{(2 h-2 a)}{3 a}+2 g(h-a)
यदि \angle LOQ=\alpha तब \alpha=\pi-\theta_1 \\ \therefore \cos \alpha=\cos \left(\pi-\theta_1\right)=-\cos \theta_1 \\ \Rightarrow \cos \alpha=\frac{2(h-a)}{3 a}
कण Q बिन्दु पर वेग V_1=\sqrt{\frac{2}{3} g(h-a)} तथा क्षैतिज के साथ कोण \alpha=\cos ^{-1}\left\{\frac{2(h-a)}{3 a}\right\} के साथ वृत्तीय पथ को छोड़ देगा
Q बिन्दु पर कण की अधिकतम ऊँचाई=H=\frac{v_1^2 \sin ^2 \alpha}{2 g}=\frac{v_1^2}{2 g}\left(1-\cos ^2 \alpha\right) \\ =\frac{1}{3}(h-a)\left[1-\frac{1}{9 a^2}(h-a)^2\right] \\ =\frac{1}{27 a^2}(h-a)\left[9 a^2-4\left(h^2-2 a h+a^2\right)\right] \\ =\frac{(h-a)}{27 a^2}\left[5 a^2+8 a h-4 h^2\right] \\ =\frac{1}{27 a^2}(h-a)(a+2 h)(5 a-2 h)
A के ऊपर कण अधिकतम ऊँचाई पर पहुँचेगा =A L+H=\frac{1}{3}(a+2 h)+\frac{1}{27 a^2}(h-a)(a+2 h) \\ =\frac{1}{274^2} \cdot(a+2 h)\left[9 a^2+(h-a)(5 a-2 h)\right] \\ =\frac{1}{27 a^2}(a+2 h)\left(4 a^2+7 a h-2 h^2\right) \\ \frac{1}{27 a^2}(a+2 h)(a+2 h)(4 a-h) \\ =27 a^2(4 a-h)(a+2 h)^2
Example:13.एक कण किसी स्थिर बिन्दु O से एक डोरी जिसकी लम्बाई a है,लटकाया हुआ है।यदि एक कील O’ पर O के क्षैतिज तल पर O से b (<a) दूरी पर हो तो सिद्ध कीजिए कि कण का इसके निम्नतम बिन्दु पर निम्निष्ट प्रक्षेप वेग \sqrt{\{g(5 a-3 b)\}} होना चाहिए जिससे वह डोरी को ढीले हुए बिना कील का पूरा चक्कर लगा सके।
(A particle is hanging from a fixed point O by means of a light string of length a.There is a small smooth nail at O’ in the same horizontal line with O at a distance b (<a) from O.Show that the minimum velocity with which the particle should be projected from its lowest position in order that it may make a complete revolution round the nail without the string becoming slack is \sqrt{\{g(5 a-3 b)\}})
Solution:माना कि m द्रव्यमान का एक कण OA डोरी जिसकी लम्बाई a से लटकाया हुआ है।माना उसी क्षैतिज रेखा में O’ एक कील है जहाँ OO’=b (<a)।माना कण A बिन्दु से u वेग से प्रक्षेपित किया जाता है।यह केन्द्र O के चारों ओर घूमता है और वृत्त की त्रिज्या a है।माना t समय पर कण की स्थिति P इस प्रकार है कि \angle AOP=\theta तथा चाप AP=s,तब
स्पर्श रेखीय तथा अभिलाम्बिक गति का समीकरण
m\left(\frac{d^2 s}{d t^2}\right)=-m g \sin \theta \cdots(1)
तथा m\left(\frac{v^2}{a}\right)=T-m g \cos \theta \cdots(2) \\ s=a \theta \cdots(3)
समीकरण (3) का (1) में प्रयोग करने पर:
a\left(\frac{d^2 \theta}{d t^2}\right)=-g \sin \theta
दोनों पक्षों को 2 a\left(\frac{d \theta}{d t}\right) गुणा करने और समाकलन करने पर:
v^2=\left[a\left(\frac{d \theta}{d T}\right)\right]^2=2ag \cos \theta+A
प्रारम्भ में A पर \theta=0 ,v=u
\therefore A=u^2-2 a g \\ \therefore v^2=u^2-2 a g+2 a g \cos \theta \cdots(4)
बिन्दु A’ पर ,\theta=\frac{\pi}{2}
यदि A’ पर वेग v_1 है तब समीकरण (4) से:
v_1^2=u^2-2ag \\ \Rightarrow v_1=\sqrt{\left(u^2-2 a g\right)}
अतः O’ पर कील है जहाँ कण वृत्तीय परिक्रमण करता है,केन्द्र O’ तथा त्रिज्या O’A’ (=a-b)
कण का वेग जब बिन्दु निम्नतम से प्रारम्भ होता है
v^2=5 a g-2 a g+2 a g \cos \theta\left[u^2=5 a g\right] \\ =3 a g+2 a g \cos \theta \\ \theta=\frac{\pi}{2} यदि v=v_2 तब v_2=\sqrt{(3 a g)}\left[\cos \frac{\pi}{2} =0\right]
इस प्रकार क्षैतिज व्यास के अन्त में कण का न्यूनतम वेग \sqrt{(3ag)} होगा जब वह वृत्त में एक पूर्ण चक्कर लगाएगा।अतः वृत्त की त्रिज्या=O’A’=a-b होने पर A’ पर कण का वेग \sqrt{[3 g(a-b)]} होना चाहिए।
परन्तु हमने पहले से ही A’ पर वेग v_{1} माना है
अतः v_{1} \geq \sqrt{[3 g(a-b)]} \\ \Rightarrow \sqrt{\left(u^2-2 a g\right)} \geq \sqrt{[3 g(a-b)]} \\ \Rightarrow u^2-2 a g \geq 3 g(a-b) \\ \Rightarrow u^2 \geq g(5 a-3 b) \\ \Rightarrow a \geq \sqrt{[g(5 a-3 b)]}
जो प्रक्षेप पर कण का न्यूनतम वेग है।
उपर्युक्त उदाहरणों के द्वारा गति विज्ञान में प्रतिबन्धित गति (Constrained Motions in Dynamics),प्रतिबन्धित गति (Constrained Motions) को समझ सकते हैं।
3.गति विज्ञान में प्रतिबन्धित गति के सवाल (Constrained Motions in Dynamics Questions):
(1.)एक कण उर्ध्वाधर वृत्त,जिसकी त्रिज्या a है में स्वतन्त्र रूप से चलता है।इसे निम्नतम बिन्दु से ऐसे वेग के साथ प्रक्षेप किया जाता है कि यह उच्चतम बिन्दु पर पहुँचता है।सिद्ध करो कि कण और तार में प्रतिक्रिया समय \sqrt{\left(\frac{a}{g}\right)} \cdot \log (\sqrt{5}+\sqrt{6}) के बाद शून्य है।
(A particle is free to move on a smooth vertical circular wire of radius a.It is projected from the lowest point with velocity just sufficient to carry it to the highest point.Show that the reaction between the particle and the wire is zero after a time \sqrt{\left(\frac{a}{g}\right)} \cdot \log (\sqrt{5}+\sqrt{6}))
(2.)एक कण a लम्बाई की डोरी से बँधा हुआ है,के निम्नतम बिन्दु से ऐसे वेग से फेंका जाता है कि वृत्ताकार पथ को छोड़ने के पश्चात कण वृत्त के निम्नतम बिन्दु से गुजरता है।सिद्ध करो कि कण का प्रक्षेप वेग \sqrt{ \left(\frac{7}{2} a g\right)} होगा:
(A particle tied to a string of length a is projected from its lowest point,so that after leaving the circular path it describes a free path passing the lowest point.Prove that the velocity of projection is \sqrt{ \left(\frac{7}{2} a g\right)}.)
उपर्युक्त सवालों को हल करने पर गति विज्ञान में प्रतिबन्धित गति (Constrained Motions in Dynamics),प्रतिबन्धित गति (Constrained Motions) को ठीक से समझ सकते हैं।
Also Read This Article:- Energy and Work in Dynamics
4.गति विज्ञान में प्रतिबन्धित गति (Frequently Asked Questions Related to Constrained Motions in Dynamics),प्रतिबन्धित गति (Constrained Motions) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रतिबन्धित गति किसे कहते हैं? (What is Constrained Motion?):
उत्तर:किसी कण की वह गति जिसमें कण किसी वक्र या पृष्ठ के सहारे चलने के लिए प्रतिबन्धित (व्यवरूद्ध) गति कहते हैं।जैसे किसी डोरी पर किसी मनके की गति अथवा किसी पृष्ठ या वक्र (गोला,चक्रज इत्यादि) के अन्दर या बाहर किसी कण की गति।
प्रश्न:2.वृत्त तथा परवलय पथ का प्रतिच्छेदन बिन्दु क्या होता है? (What is the Point of Intersection of the Circle and Parabolic Path?):
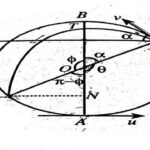
उत्तर:एक कण a त्रिज्या वाले किसी चिकने उर्ध्वाधर वृत्त के सबसे नीचे के बिन्दु से u वेग से फेंका जाता है।यहाँ ।इसकी गति की विवेचना करना:
(A particle is projected from the lowest point of a smooth vertical circle of radius a with velocity u where.To discuss its motion):
यदि कण को निम्नतम बिन्दु से एक ऐसे वेग u,जहाँ 2 a g < u^2<5 a g से प्रक्षेपित किया जाये जो उपर्युक्त प्रकार से कण वृत्त को 90^{\circ}<\theta<180^{\circ} के लिए किसी बिन्दु P पर छोड़ देगा जहाँ R=0 अर्थात् जिसके लिए \cos \theta=\frac{2 a g-a^2}{3 a g}
अब यदि \angle P O B=\alpha तो \alpha=\pi-\theta \\ \therefore \cos \alpha= \cos (\pi-\theta) =-\cos \theta=\frac{4^2-2 a g}{3 a g} \cdots(1)
यदि बिन्दु P पर कण का वेग v हो तो
v^2=u^2-2 a g+2 a g \cos \theta \\ =u^2-2 a g+2 a g \frac{2 a g-u^2}{3 a g} \\ \Rightarrow v^2=\frac{u^2-2 a g}{3}=a g \cos \alpha [(1) से]………(2)
अब यदि P को मूलबिन्दु लें,PX तथा PY से x-अक्ष तथा y-अक्ष लें,तो PX के साथ कोण बनाती है।कण का प्रक्षेप पथ (परवलय पथ) का समीकरण होगा:
y=x \tan \alpha-\frac{1}{2} \frac{2 x^2}{v^2 \cos ^2 \alpha} \\ \Rightarrow y=x \tan \alpha-\frac{1}{2} \frac{x^2}{a^2 \cos ^2 \alpha} [(2) से]
वृत्त तथा परवलय पथ का प्रतिच्छेद बिन्दु (The point of intersection of the circle and the parabolic path):
PX,PY अक्षों के सापेक्ष वृत्त के केन्द्र के निर्देशांक (a \sin \alpha,-a \cos \alpha) हैं।
अतः वृत्त का समीकरण होगा:
(x-a \sin \alpha)^2+(y+a \cos \alpha)^2=a^2 \\ \Rightarrow x^2+y^2-2 a x \sin \alpha+2 a y \cos \alpha=0
अब हम इस समीकरण को हम निम्न प्रकार लिख सकते हैं:
y=x \tan \alpha-\frac{x^2+y^2}{2 a \cos \alpha} \cdots(4)
परवलय तथा वृत्त के समीकरणों [अर्थात् समीकरण (3) तथा (4)] को हल करने पर:
\frac{x^2}{2 a \cos ^3 \alpha}=\frac{x^2+y^2}{2 a \cos \alpha} \\ \Rightarrow x+y^2=x^2 \sec ^2 \alpha \\ \Rightarrow y= \pm x \tan \alpha
अब y=x \tan \alpha समीकरण (4) में रखने पर:
x=0,y=0 अर्थात् बिन्दु P के निर्देशांक (0,0) हैं।
एवं y=-x \tan \alpha समीकरण (4) में रखने पर:
-x \tan \alpha=x \tan \alpha-\frac{x^2}{2 a \cos ^3 \alpha} \\ \Rightarrow x=4 a \cos ^2 \alpha \cdot \sin \alpha= \ \Rightarrow y=-4 a \cos \alpha \sin ^2 \alpha
अतः वृत्त एवं परवलीय पथ का प्रतिच्छेद बिन्दु D है और D के निर्देशांक (4 a \cos ^2 \alpha \cdot \sin \alpha,-4 a \cdot \cos \alpha \sin ^2 \alpha) हैं।
प्रश्न:3.परवलय पथ का नाभिलम्ब कैसे ज्ञात करते हैं? (How to Find Letus Rectum of the Parabolic Path?):
उत्तर:कण के प्रक्षेप-पथ (परवलय) का नाभिलम्ब (L.R.)
=\frac{\text{2(बिन्दु P पर कण के वेग का क्षैतिज घटक)}^2}{g} \\ =\frac{2 v^2 \cos ^2 \alpha}{2} \\ =\frac{2 a g \cos ^3 \alpha}{g} \\ =2 a \cos ^3 \alpha \cdots(3)\\ =2 a\left(\frac{u^2-2 a g}{3 a g}\right)^3 [(1) का मान रखने पर]
=\frac{2\left(a^2-2 a g\right)^{33}}{27 a^2 g^3}
उपर्युक्त प्रश्नों के उत्तर द्वारा गति विज्ञान में प्रतिबन्धित गति (Constrained Motions in Dynamics),प्रतिबन्धित गति (Constrained Motions) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Constrained Motions in Dynamics
गति विज्ञान में प्रतिबन्धित गति
(Constrained Motions in Dynamics)
Constrained Motions in Dynamics
गति विज्ञान में प्रतिबन्धित गति (Constrained Motions in Dynamics) पर आधारित कुछ सवालों
का हल इससे पूर्व आर्टिकल में कर चुके हैं।इस आर्टिकल में कुछ ओर सवालों को हल करके
समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.











