Congruence of triangles in class 9
1.कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of triangles in class 9)-
कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of triangles in class 9) को समझने के लिए हमें सर्वांगसमता का अर्थ,सर्वांगसमता के नियमों तथा त्रिभुजों के अन्य गुणधर्मों को समझना आवश्यक है।
(1.) त्रिभुजों की सर्वांगसमता (Congruence of triangles)-
हम दैनिक जीवन में बहुत सी आकृतियां समान माप तथा आकार की देखते हैं।जैसे-एक ही माप की पुस्तकें,एक ही माप की माचिस तथा फोटोयुक्त डाक टिकट।ऐसी सभी आकृतियां सर्वांगसम (identical) होती है।
यदि इनमें से किन्हीं भी दो सर्वसम आकृतियों का चयन करके एक-दूसरे पर रखेंगे तो वे एक-दूसरे को पूर्णतया ढक लेती है।
त्रिभुजों की सर्वांगसमता (Congruence triangles meaning) का अर्थ है कि वे त्रिभुज जिनका आकार व माप समान हो सर्वांगसम त्रिभुज कहलाते हैं।
(2.)प्रमेय (Theorem):कोण-भुजा-कोण नियम (ASA Rule)-
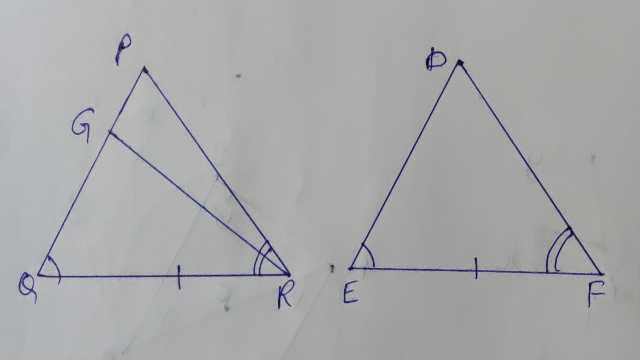
यदि त्रिभुज के कोई दो कोण और उनकी अन्तरित भुजा दूसरे त्रिभुज के दो कोणों और उनकी अन्तरित भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं।
दिया है(Given):PQR एवं DEF दो त्रिभुज हैं,जहां\angle PQR=\angle DEF,\angle PRQ=\angle DFE एवं QR=EF
सिद्ध करना है (To Prove):\\ \triangle PQR\cong \triangle DEF
उपपत्ति (Proof): दोनों त्रिभुजों PQR एवं DEF की भुजा PQ एवं DE की तुलना करने पर-
तीन स्थितियां सम्भव है:
(i) PQ=DE (ii) PQ<DE (iii) PQ>DE
स्थिति-I यदि PQ=DE हो तो
\triangle PQR तथा \triangle DEF में
PQ=DE (माना)
\angle PQR=\angle DEF(दिया है)
RQ=EF (दिया है)
भुजा-कोण-भुजा नियम (SAS)से
\triangle PQR\cong \triangle DEF
स्थिति-II जब PQ<DE हो तो भुजा DE पर एक बिन्दु G इस प्रकार लिया कि PQ=GE एवं GF को मिलाया।
\triangle PQRतथा\triangle DEFमें
PQ=GE (माना)
QR=EF (दिया है)
\angle PQR=\angle GEF(दिया है)[\because \angle GEF=\angle DEF]
भुजा-कोण-भुजा नियम (SAS)से
\triangle PQR\cong \triangle GEF
अतः\angle PRQ=\angle GFE….(1)
एवं\angle PRQ=\angle DEF(दिया है)…(2)
समीकरण (1) एवं (2) से-
\angle GFE=\angle DFEजो तब तक असंभव है जब तक GF,DF के साथ सम्पाती न हो जाए अर्थात्
G एवं D सम्पाती है अतः \therefore PQ=DE
भुजा-कोण-भुजा नियम (SAS)से
\triangle PQR\cong \triangle DEF
स्थिति-III जब AB>DE हो तो चित्र के अनुसार \triangle PQR में भुजा PQ पर एक बिन्दु इस प्रकार लिया कि QG=ED
\triangle GQRतथा \triangle DEF में
GQ=DE (माना)
QR=EE (दिया है)
\angle GQR=\angle DEF (दिया है)[\because \angle PQR=\angle GQR]
भुजा-कोण-भुजा सर्वांगसमता (SAS) से
\triangle GQR\cong \triangle DEF
अतः\angle GRQ=\angle DFE…..(3)
तथा \angle PRQ=\angle DEF(दिया है)…(4)
यह तभी संभव है जबकि G व D संपाती हो।
PQ=DE
अतः भुजा-कोण-भुजा नियम (ASA) से
\triangle PQR\cong \triangle DEF
इसलिए तीनों स्थितियों में
\triangle PQR\cong \triangle DEF
त्रिभुजों के तीनों अन्त: कोणों का योग होता है इसलिए जब त्रिभुज के दो कोण,त्रिभुज दो कोणों के बराबर हों तो त्रिभुजों के तीसरे कोण स्वत: समान हों जाएंगे।इस नियम के आधार पर निम्न उप-प्रमेय सिद्ध करेंगे।
उप-प्रमेय:कोण-कोण-भुजा नियम (AAS)
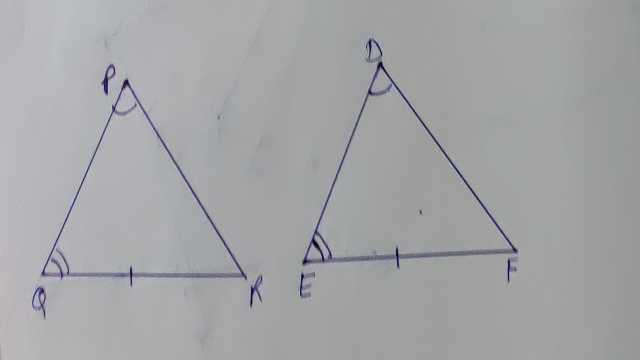
यदि एक त्रिभुज के कोण और एक भुजा दूसरे त्रिभुज के दो संगत कोणों और संगत भुजा के बराबर हों तो त्रिभुज सर्वांगसम होते हैं।
दिया है (Given): \triangle PQR तथा \triangle DEF में \angle Q=\angle E,\angle P=\angle Dएवं भुजा QR=EF
सिद्ध करना है (To Prove):\triangle PQR\cong \triangle DEF
उपपत्ति (Proof):हम जानते हैं कि त्रिभुज के तीनों कोणों का योग होता है, अतः
\angle P+\angle Q+\angle R={ 180 }^{ 0 }\qquad ..................(1)\\ \angle D+\angle E+\angle F={ 180 }^{ 0 }\qquad ..................(2)
समीकरण (1) में \angle Q=\angle E तथा \angle P=\angle D (दिया है) रखने पर-
\angle D+\angle E+\angle R={ 180 }^{ 0 }.........(3)
समीकरण (2) तथा (3) से-
\angle D+\angle E+\angle R=\angle D+\angle E+\angle F\\ \Rightarrow \angle R=\angle F.............(4)\\ \triangle PQR तथा \triangle DEF में
\angle Q=\angle E(दिया है)
QR=EF (दिया है)
\angle R=\angle F[(4) से]
कोण-भुजा-कोण नियम (ASA) से
\triangle PQR\cong \triangle DEF
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।
यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Best tips to get 100 marks in maths
2.कक्षा 9 में त्रिभुजों की सर्वांगसमता उदाहरण (Congruence of triangles in class 9 examples)-
Example-1. चित्र में चतुर्भुज ABCD का विकर्ण AC शीर्ष कोण A एवं C का समद्विभाजन हो तो सिद्ध कीजिए AB=CD एवं CB=CD
Solution-दिया है (Given): चतुर्भुज ABCD में AC ,शीर्ष कोण A व C का समद्विभाजक है अर्थात् \angle BAC=\angle DAC,\angle BCA=\angle DCA
सिद्ध करना है (To Prove):AB=CD एवं CB=CD
उपपत्ति (Proof): \triangle ABC तथा \triangle ADCमें
\angle BAC=\angle DAC(दिया है)
AC=AC (उभयनिष्ठ भुजा है)
\angle BCA=\angle DCA(दिया है)
अतः कोण-भुजा-कोण सर्वांगसमता (ASA) से
\triangle ABC\cong \triangle ADC
अतःAB=CD एवं CB=CD
(सर्वांगसम त्रिभुजों की संगत भुजा बराबर होती है)
Example-2.चित्र में चतुर्भुज ADBC के एवं BC=BD हो तो सिद्ध कीजिए कि \triangle ABC\cong \triangle ABD
Solution- दिया है (Given): चतुर्भुज ADBC में\angle ABC=\angle ABD,BC=BD
सिद्ध करना है (To Prove):\triangle ABD\cong \triangle ABD
उपपत्ति (Proof): \triangle ABC तथा \triangle ABD में
AB=AB (उभयनिष्ठ भुजा है)
\angle ABC=\angle ABD(दिया है)
BC=BD (दिया है)
भुजा-कोण-भुजा सर्वांगसमता (SAS Congruence) से
\triangle ABC\cong \triangle ABD
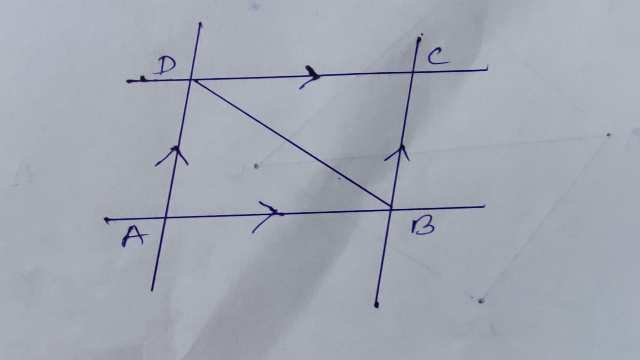
Example-3.चित्र के अनुसारAB\parallel DC एवं AD\parallel BC हो तो सिद्ध कीजिए:\triangle ADB\cong \triangle CBD
Solution- दिया है (Given): AB\parallel DC एवं AD\parallel BC
सिद्ध करना है (To Prove):-\triangle ADB\cong \triangle CBD
उपपत्ति (Proof): AB\parallel DCतथा तिर्यक रेखा BD इनको काटती है
अतः\angle ABD=\angle CDB (एकान्तर कोण)…(1)
इसी प्रकार AD\parallel BC तथा तिर्यक रेखा BD इनको काटती है
\angle ADB=\angle CBD(एकान्तर कोण)….(2)
\triangle ADB तथा\triangle CBD में
\angle ABD=\angle CDB[(1) से]
BD=BD (उभयनिष्ठ भुजा है)
\angle ADB=\angle CBD[(2) से ]
कोण-भुजा-कोण सर्वांगसमता (ASA Congruence) से
\triangle ADB\cong \triangle CBD
Example-4. चित्र में यदि AB\parallel DC एवं E भुजा AC का मध्यबिन्दु हो तो सिद्ध कीजिए कि E ,भुजा BD का मध्यबिन्दु होगा।
Solution- दिया है (Given): AB\parallel DC एवं AE=CE
सिद्ध करना है (To Prove): BE=DE
उपपत्ति (Proof): AB\parallel DCतथा तिर्यक रेखा AC व BD इनको काटती है
अतः \angle BAE=\angle DCE (एकान्तर कोण)….(1)
\angle ABE=\angle CDE (एकान्तर कोण)….(2)
\triangle ABE तथा \triangle CDEमें
\angle BAE=\angle DCE [(1) से]
AE=CE (दिया है)
\angle AEB=\angle CED[शीर्षाभिमुख कोण]
[कोण-भुजा-कोण सर्वांगसमता (ASA Congruence) से]
\triangle ABE\cong \triangle CDE
BE=DE
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
Example-5. चित्र में AD=BC एवं BD=CA हो तो सिद्ध कीजिए कि
(i)\angle ADB=\angle BCA\\ (ii)\angle DAB=\angle CBA
Solution- दिया है (Given):AD=BC एवं BD=CA
सिद्ध करना है (To Prove):(i)\angle ADB=\angle BCA\\ (ii)\angle DAB=\angle CBA
उपपत्ति (Proof):\triangle ADB तथा \triangle BCA में
AD=BC (दिया है)
BD=AC (दिया है)
AB=AB (उभयनिष्ठ भुजा है)
भुजा-भुजा-भुजा गुणधर्म (SSS Congruence) से
\triangle ADB\cong \triangle BCA\\ \angle ADB=\angle BCA\\ \angle DAB=\angle CBA
[सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं]
उपर्युक्त उदाहरणों के द्वारा कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of triangles in class 9) को समझ सकते हैं।
3.सर्वांगसम त्रिभुज की समस्याएं (Congruence triangles Problems)-
(1.)चित्र में AB का मध्यबिन्दु C है, \angle BCD=\angle ACE एवं \angle DAB=\angle EBAहो,तो सिद्ध कीजिए कि:
(i)\triangle DAC\cong \triangle EBC\\ (ii)DA=EB
(2.)चित्र में एक चतुर्भुज ABCD BC=AD एवं \angle ADC=\angle BCD हो,तो सिद्ध कीजिए: (i)AC=BD\\ (ii)\angle ACD=\angle CDB
(3.) चित्र में,AE=EC एवं DE=BE हो तो सिद्ध कीजिए कि:
(i)\triangle AED\cong \triangle CEB\\ (ii)\angle A=\angle C
Congruence of triangles in class 9
उपर्युक्त कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of triangles in class 9) की समस्याओं को हल करने पर सर्वांगसमता ठीक से समझ आ जाएगी।
4.त्रिभुजों की सर्वांगसमता के 4 परीक्षण क्या है?,SSS,SAS,ASA,AAS सर्वांगसमता क्या है? (What are the 4 tests of congruence in a triangle?,What is SSS SAS ASA and AAS congruence?)-
दो त्रिभुजों के सर्वांगसमता होने के पांच तरीके हैं:SSS, SAS, ASA, AAS and HL.
SSS (side, side, side) SSS,side,side,side के लिए प्रयुक्त है और इसका मतलब है कि हमारे पास तीनों भुजाओं के साथ दो त्रिभुज समान हैं।
SAS (side, angle, side)
ASA (angle, side, angle)
AAS (angle, angle, side)
HL (hypotenuse, leg)
5.क्या AAA नियम से त्रिभुज सर्वांगसम हो सकते हैं? (Can triangles be congruent by AAA?)-
AAA का मतलब है कि हमें एक त्रिभुज के सभी तीन कोण दिए गए हैं, लेकिन कोई भुजा नहीं। यह तय करने के लिए पर्याप्त जानकारी नहीं है कि क्या दो त्रिकोण सर्वांगसम हैं!
6.त्रिभुजों की सर्वांगसमता की शर्त (conditions for congruence of triangles)-
सर्वांगसमता का निर्धारण
SSS (side-side-side): यदि दो त्रिभुज की भुजाओं के तीन जोड़े लंबाई में समान हैं,तो त्रिभुज सर्वांगसम हैं।ASA (angle-side-angle): यदि माप में दो त्रिभुज के कोणों के दो जोड़े बराबर हैं, और शामिल भुजाएं लंबाई में बराबर हैं, तो त्रिभुज सर्वांगसम हैं।
7.आपको कैसे पता चलेगा कि त्रिभुज सर्वांगसम हैं? (How do you know if triangles are congruent?)-
सर्वांगसमता का निर्धारण
SSS (side-side-side): यदि दो त्रिभुज की भुजाओं के तीन जोड़े लंबाई में समान हैं,तो त्रिभुज सर्वांगसम हैं।ASA (angle-side-angle): यदि माप में दो त्रिभुज के कोणों के दो जोड़े बराबर हैं,और शामिल भुजा लंबाई में बराबर हैं, तो त्रिभुज सर्वांगसम हैं।
Also Read This Article:-Use of models in mathematics
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | click here | |
| 6. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
