Conditional Probability
1.सप्रतिबन्ध प्रायिकता (Conditional Probability),सप्रतिबन्ध प्रायिकता सूत्र (Conditional Probability Formula):
सप्रतिबन्ध प्रायिकता (Conditional Probability) का अध्ययन करने से पूर्व समसंभाव्य परिणामों की अवस्था में प्रायिकता के अभिगृहीत दृष्टिकोण तथा चिरसम्मत सिद्धान्त का अध्ययन करना आवश्यक है।इस आर्टिकल में किसी घटना की सप्रतिबन्ध प्रायिकता (जब एक घटना घटित हो चुकी हो तथा दूसरी घटित हो रही हो) का अध्ययन करेंगे।सप्रतिबन्ध प्रायिकता की अवधारणा की सहायता से स्वतन्त्र घटनाओं, प्रायिकता के गुणन नियम,प्रतिलोम प्रायिकता ज्ञात करने के लिए बेज प्रमेय के बारे में समझेंगे।अन्त में यादृच्छिक चर तथा इसके प्रायिकता बंटन व किसी प्रायिकता बंटन के माध्य व प्रसरण का अध्ययन करेंगे।
सप्रतिबन्ध प्रायिकता (Conditional Probability):
सप्रतिबन्ध प्रायिकता को समझने के लिए एक ऐसे यादृच्छिक परीक्षण पर विचार करते हैं जिसके परिणाम समसंभाव्य है।दो न्याय्य सिक्कों को उछालने के परीक्षण पर विचार करते हैं जिसका प्रतिदर्श समष्टि निम्न है:
S={HH,HT,TH,TT} जहाँ H=चित्त,T=पट
चूँकि दोनों सिक्के न्याय्य है अतः हम प्रतिदर्श समष्टि के प्रत्येक प्रतिदर्श बिन्दु की प्रायिकता \frac{1}{4} निर्दिष्ट कर सकते हैं।माना A घटना “कम से कम एक चित्त प्रकट होना” को निरूपित करते हैं।
तब A={HT,TH,HH},B={TH,TT}
अतः P(A)=P({HT})+P({TH})+P({HH}) =\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{3}{4}
तथा P(B)=P({TH})+P({TT}) =\frac{1}{4}+\frac{1}{4} \\ =\frac{1}{2}
साथ ही A \cap B=\{T H\}
अतः P(A \cap B)=P(\{T H\})=\frac{1}{4}
अब माना हमें घटना A की प्रायिकता ज्ञात करनी है जबकि घटना B घटित हो चुकी हो।घटना B के घटित होने की जानकारी होने पर यह निश्चित है कि घटना A की प्रायिकता ज्ञात करने के लिए उन प्रतिदर्श बिंदुओं पर विचार नहीं किया जाएगा जिनमें पहले सिक्के पर पट नहीं है।अतः घटना B का वह प्रतिदर्श बिन्दु जो घटना A के भी अनुकूल है;TH है।
B को प्रतिदर्श समष्टि मानते हुए घटना A की प्रायिकता या घटना
A के घटित होने की प्रायिकता जबकि घटना B घटित हो चुकी हो=\frac{1}{2}
घटना A की यह प्रायिकता सप्रतिबंध प्रायिकता कहलाती है तथा इसे P\left(\frac{A}{B}\right) से निरूपित करते हैं।
अर्थात् P\left(\frac{A}{B}\right)=\frac{1}{2}
घटना A की सप्रतिबन्ध प्रायिकता को निम्न प्रकार से ज्ञात किया जा सकता है।
P\left(\frac{A}{B}\right) =\frac{ n(A \cap B) \text{ के अनुकूल प्रतिदर्श बिन्दुओं की संख्या}}{\text{ B के अनुकूल प्रतिदर्श बिन्दुओं की संख्या }} \\ =\frac{n(A \cap B)}{n(B)}
अंश व हर को प्रतिदर्श समष्टि के अवयवों की कुल संख्या से विभाजित करने पर P\left(\frac{A}{B}\right) को निम्न प्रकार से व्यक्त किया जा सकता है: P\left(\frac{A}{B}\right) =\frac{\frac{n(A \cap B)}{n(S)}}{\frac{n(B)}{n(S)}} \\=\frac{P(A \cap B)}{P(B)}
जो केवल तभी वैध है जबकि P(B) \neq 0
सप्रतिबन्ध प्रायिकता परिभाषा (Conditional Probability Definition):यदि किसी यादृच्छिक परीक्षण के प्रतिदर्श समष्टि से सम्बन्धित A तथा B दो घटनाएं हो तो घटना B के घटित होने की जानकारी होने पर घटना A की सप्रतिबन्ध प्रायिकता निम्न सूत्र से ज्ञात की जाती है:
P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)} ; P(B) \neq 0
इसी प्रकार घटना A के घटित होने की जानकारी होने पर घटना B की सप्रतिबन्ध प्रायिकता निम्न सूत्र से ज्ञात की जा सकती है:
P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)} ; P(A) \neq 0
सप्रतिबन्ध प्रायिकता के गुणधर्म (Properties of Conditional Probability):
माना A तथा B किसी प्रतिदर्श समष्टि S की दो घटनाएँ है तब
(i) P\left(\frac{S}{B}\right)=P\left(\frac{B}{B}\right)=1
हम जानते हैं कि P\left(\frac{S}{B}\right)=\frac{P(S \cap B)}{P(B)}=\frac{P(B)}{P(B)}=1
पुनः P\left(\frac{B}{B}\right)=\frac{P(B \cap B)}{P(B)}=\frac{P(B)}{P(B)}=1
अतः P\left(\frac{S}{B}\right)=P\left(\frac{B}{B}\right)=1 \\ \text { (ii) } P\left(\frac{A}{B}\right)=1-P\left(\frac{A}{B}\right)
गुणधर्म (i) से P\left(\frac{S}{B}\right)=1 \\ \Rightarrow P\left(\frac{A \cup \bar {A}}{B}\right)=1[\because S=A \cup \bar{A}] \\ \Rightarrow P\left(\frac{A}{B}\right)+P\left(\frac{\bar {A}}{B}\right)=1
[A तथा \bar {A} परस्पर अपवर्जी घटनाएं हैं]
अतः P\left(\frac{\bar{A}}{B}\right)=1-P\left(\frac{A}{B}\right)
(iii)यदि प्रतिदर्श समष्टि S की A तथा B कोई दो घटनाएं हो तथा B कोई दो घटनाएं हो तथा F एक अन्य घटना इस प्रकार से हो कि
P(F) \neq 0 तब
\text { (a) }P\left(\frac{A \cup B}{F}\right) =P\left(\frac{A}{F}\right)+P\left(\frac{B}{F}\right) -P\left(\frac{A \cap B}{F}\right)
तथा यदि A व B परस्पर अपवर्जी घटनाएं हो तो
\text { (b) } P\left(\frac{A \cup B}{F}\right)=P\left(\frac{A}{F}\right)+P\left(\frac{B}{F}\right)
हम जानते हैं कि
P\left(\frac{A \cup B}{F}\right)=\frac{P[(A \cup B) \cap F]}{P(F)} \\ =\frac{P[A \cap F) \cup(B \cap F)]}{P(F)} \\=\frac{P(A \cap F)+P(B \cap F)-P(A \cap B \cap F)}{P(F)} \\ =\frac{P(A \cap F)}{P(F)}+\frac{P(B \cap F)}{P(F)}-\frac{P[(A \cap B) \cap F]}{P(F)} \\ = P\left(\frac{A}{F}\right)+P\left(\frac{B}{F}\right)-P\left(\frac{A \cap B}{F}\right)
विशेष स्थिति:यदि A तथा B परस्पर अपवर्जी घटनाएं हों तो
P\left(\frac{A \cap B}{F}\right)=0
अतः P\left(\frac{A \cup B}{F}\right)=P\left(\frac{A}{F}\right)+P\left(\frac{B}{F}\right)
अतःआपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Basic Properties of Definite Integrals
2.सप्रतिबन्ध प्रायिकता के उदाहरण (Conditional Probability Examples):
Example:1.यदि P(A)=\frac{7}{13}, P(B)=\frac{9}{13} और P(A \cap B)=\frac{4}{13} हो तो P\left(\frac{A}{B}\right) ज्ञात कीजिए।
Solution:दिया है P(A)=\frac{7}{13}, P(B)=\frac{9}{13} और P(A \cap B)=\frac{4}{13} \\ P\left(\frac{A}{B}\right) =\frac{P(A \cap B)}{P(B)} \\ =\frac{\frac{4}{13}}{\frac{9}{13}} \\ P\left(\frac{A}{B}\right) =\frac{4}{9}
Example:2.यदि P(B)=0.5 और P(A \cap B)=0.32 हो तो P\left(\frac{A}{B}\right) ज्ञात कीजिए।
Solution:दिया है P(B)=0.5 ,P(A \cap B)=0.32 \\ \\ P\left(\frac{A}{B}\right) =\frac{P(A \cap B)}{P(B)} \\ =\frac{0.32}{0.5} \\ =\frac{32 \times 10}{5 \times 100} \\ \Rightarrow P\left(\frac{A}{B}\right)=\frac{16}{25}
Example:3.यदि 2 P(A)=P(B)=\frac{5}{13} और P\left(\frac{A}{B}\right)=\frac{2}{5} हो तो P(A \cup B) ज्ञात कीजिए।
Solution:2 P(A)=\frac{5}{13} \Rightarrow P(A)=\frac{5}{26} \\ P(B)=\frac{5}{13}, P\left(\frac{A}{B}\right)=\frac{2}{5}, P(A \cup B)=? \\ P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)} \\ \Rightarrow \frac{2}{5}=\frac{P(A \cap B)}{\frac{5}{13}} \\ \Rightarrow P(A \cap B)=\frac{2}{5} \times \frac{5}{13} \\ \Rightarrow P(A \cap B)=\frac{2}{13}\\ P(A \cap B)=P(A)+P(B)-P(A \cap B) \\ P(A \cap B) =\frac{5}{26}+\frac{5}{13}-\frac{2}{13} \\ =\frac{5+10-4}{26}=\frac{11}{26} \\ P(A \cap B) =\frac{11}{26}
Example:4.यदि P(A)=0.6,P(B)=0.3 और P(A \cap B)=0.2 हो तो P\left(\frac{A}{B}\right) तथा P\left(\frac{B}{A}\right) ज्ञात कीजिए।
Solution:दिया है P(A)=0.6,P(B)=0.3,P(A \cap B)=0.2\\ P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)} \\ \Rightarrow P\left(\frac{A}{B}\right)=\frac{0.2}{0.3} \\ \Rightarrow P\left(\frac{A}{B}\right)=\frac{2}{3} \\ P\left(\frac{B}{A}\right)= \frac{P(A \cap B)}{P(A)} \\ \Rightarrow P\left(\frac{B}{A}\right)=\frac{0.2}{0.6} \\ \Rightarrow P\left(\frac{B}{A}\right)=\frac{1}{3}
Example:5.यदि P(A)=0.8,P(B)=0.5 और P\left(\frac{B}{A}\right)=0.4 हो तो ज्ञात कीजिए।
\text { (i) } P(A \cap B) \text { (ii) } P\left(\frac{A}{B}\right) \text { (iii) } P(A \cup B)
Solution:(i) P(A \cap B) =P(A) \cdot P\left(\frac{B}{A}\right) \\ =(0.8)(0.4) \\ \Rightarrow P(A \cap B) =0.32 \\ \text { (ii) } P\left(\frac{A}{B}\right) =\frac{P(A \cap B)}{P(B)} \\ =\frac{0.32}{0.5} \\ =\frac{32}{50} \\ =\frac{16}{25}=0.64 \\ \text { (iii) } P(A \cup B) =P(A)+P(B)-P(A \cap B) \\ =0.8+0.5-0.32 \\ =1.3-0.32 \\ \Rightarrow P(A \cup B) =0.98
Example:6.एक परिवार में दो बच्चे हैं।यदि यह ज्ञात हो कि दोनों बच्चों में से कम से कम एक बच्चा लड़का है तो दोनों बच्चों के लड़का होने की प्रायिकता ज्ञात कीजिए।
Solution:दो बच्चे होने की प्रतिदर्श समष्टि S={BB,BG,GB,GG}
A=कम से कम एक बच्चा लड़का होने की घटना=
C=दोनों बच्चों के लड़का होने की घटना
A \cap C={BB}
A={BB,BG,GB}
n(A)=3 ,n(A \cap C)=1\\ P\left(\frac{C}{A}\right)=\frac{P(A \cap C)}{P(A)}\\ =\frac{n(A \cap C)}{n(A)}\\ \Rightarrow P\left(\frac{C}{A}\right)=\frac{1}{3}
Example:7.दो सिक्कों को एक बार उछाला गया है इस प्रयोग से सम्बन्धित घटनाओं A व B को निम्न प्रकार परिभाषित किया गया है तो P(\frac{A}{B}) ज्ञात कीजिए।
(i)A:एक सिक्के पर पट प्रकट होता है;B:एक सिक्के पर चित्त प्रकट होता है।
(ii)A:कोई पट प्रकट नहीं होता;B:कोई चित्त प्रकट नहीं होता।
Solution:दो सिक्कों को उछालने पर प्रतिदर्श समष्टि S={HH,HT,TH,TT}
A=एक सिक्के पर पट प्रकट होना={HT,TH}
B=एक सिक्के पर चित्त प्रकट होना={HT,TH}
A \cap B={HT,TH},\quad n(B)=2 ,\quad n(A \cap B)=2 \\ P(B)=\frac{2}{4}=\frac{1}{2}, \quad P(A \cap B)=\frac{2}{4}=\frac{1}{2} \\ P(\frac{A}{B})=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{2}}{\frac{1}{2}}=1
(ii)A=कोई पट प्रकट नहीं होता={HH}
B=कोई चित्त प्रकट नहीं होता={TT}
A \cap B =\phi ,\quad P(A)=\frac{1}{4}, P(B)=\frac{1}{4}, P(A \cap B)=0 \\ P(\frac{A}{B}) =\frac{P(A \cap B)}{P(B)} \\ =\frac{0}{\frac{1}{4}}=0
Example:8.एक पारिवारिक चित्र में माता,पिता व पुत्र यादृच्छया सीधी रेखा में खड़े हैं।इससे सम्बद्ध घटनाओं A व B को निम्न प्रकार परिभाषित किया गया है तो P(\frac{A}{B}) ज्ञात कीजिए।यदि
A:पुत्र एक सिरे पर खड़ा है,B:पिता मध्य में खड़े हैं
Solution:माना माता (M),पिता (F) तथा पुत्र (S) यादृच्छया खड़े हैं।
माता, पिता और पुत्र के खड़े होने की प्रतिदर्श समष्टि={MFS,MSF,SMF,SFM,FMS,FSM}
A=पुत्र के सिरे पर खड़े होने की घटना ={MFS,SMF,SFM,FMS}
B=पिता के मध्य में खड़े होने की घटना ={MFS,SFM}
P(A \cap B)={MFS,SFM}
P(B)=\frac{2}{6}=\frac{1}{3}, \quad P(A \cap B)=\frac{2}{6}=\frac{1}{3}\\ P(\frac{A}{B})=\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{3}}{\frac{1}{3}}=1
Example:9.एक न्याय्य पासे को उछाला गया है।घटनाओं A={1,3,5},B={2,3} व C={2,3,4,5} के लिए निम्नलिखित ज्ञात कीजिए।
(i)P\left(\frac{A}{B}\right) \text { व } P\left(\frac{B}{A}\right) (ii)P\left(\frac{A}{C}\right) \text { व } P\left(\frac{C}{A}\right) (iii)P\left(\frac{A \cup B}{C}\right) \text { व } P\left(\frac{A \cap B}{C}\right)
Solution:दिया है A={1,3,5},B={2,3} C={2,3,4,5}
एक न्याय्य पासे को उछालने पर प्रतिदर्श समष्टि= {1,2,3,4,5,6}
P(A)=\frac{3}{6}=\frac{1}{2},P(B)=\frac{2}{6}=\frac{1}{3},P(C)=\frac{4}{6}=\frac{2}{3} \\ A \cap B=\left \{ 3 \right \} ,P(A \cap B)=\frac{1}{6} \\ A \cup C=\left \{ 3,5 \right \} \Rightarrow P(A \cap C)=\frac{2}{6}=\frac{1}{3} \\ \text {(i) }P(\frac{A}{B}) =\frac{P(A \cap B)}{P(B)}=\frac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{2} \\ \Rightarrow P\left(\frac{B}{A}\right)=\frac{P(A \cap B)}{P(A)} \\ \Rightarrow P\left(\frac{B}{A}\right)=\frac{\frac{1}{6}}{\frac{1}{2}}=\frac{1}{3} \\ \text {(ii) } P\left(\frac{A}{C}\right) =\frac{P(A \cap C)}{P(C)} \\ =\frac{\frac{1}{3}}{\frac{2}{3}} \\ \Rightarrow P\left(\frac{A}{C}\right) =\frac{1}{2} \\ P\left(\frac{C}{A}\right) =\frac{P(A \cap C)}{P(A)} \\=\frac{\frac{1}{3}}{\frac{1}{2}} \\ P\left(\frac{C}{A}\right) =\frac{2}{3} \\ \text {(iii) } P\left(\frac{A \cup B}{C}\right)=P\left(\frac{A}{C}\right)+ P\left(\frac{B}{C}\right)-P\left(\frac{A \cap B}{C}\right) \\ P\left(\frac{A \cup B}{C}\right)=P\left(\frac{A}{C}\right)+P\left(\frac{B}{C}\right)-P\left(\frac{A \cap B}{C}\right) \\ =\frac{P\left(A \cap C\right)}{P(C)}+\frac{P\left(B \cap C\right)}{P(C)}-\frac{P\left \{ \left(A \cap B\right) \cap C \right \}}{P(C)} \\ =\frac{\frac{1}{3}}{\frac{2}{3}}+\frac{\frac{2}{6}}{\frac{2}{3}}-\frac{\frac{1}{6}}{\frac{2}{3}} \\ =\frac{1}{2}+\frac{1}{2}-\frac{1}{4} \\ =\frac{2+2-1}{4} \\ =\frac{3}{4} \\ \Rightarrow P\left(\frac{A \cup B}{C}\right)=\frac{3}{4} \\ P\left(\frac{A \cap B}{C}\right)=\frac{P\{(A \cap B) \cap C\}}{P(C)} \\ A \cap B=\{3\}, n(A \cap B)=1 \\ P(A \cap B)=\frac{1}{6} \\ (A \cap B) \cap C=\{3\}, n(A \cap B) \cap C\}=1 \\ P\{(A \cap B) \cap C\}=\frac{1}{6} \\ P\left(\frac{A \cap B}{C}\right)=\frac{\frac{1}{6}}{\frac{2}{3}}=\frac{1}{4}
Example:10.यह दिया गया है कि दो पासों को फेंकने पर प्राप्त अंक भिन्न-भिन्न है।दोनों पासों पर प्राप्त अंकों का योग 4 होने की प्रायिकता ज्ञात कीजिए।
Solution:दो पासों को फेंकने पर प्रतिदर्श समष्टि
\begin{array}{lllllll} & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 1 & (1,1) & (1,2) & (1,3) & (1,4)&(1,5)&(1,6) \\ 2 & (2,1) & (2,2) & (2,3) & (2,4)&(2,5)&(2,6) \\ 3 & (3,1) & (3,2) & (3,3) & (3,4)&(3,5)&(3,6) \\ 4 & (4,1) & (4,2) & (4,3) & (4,4)&(4,5)&(4,6) \\ 5 & (5,1) & (5,2) & (5,3) & (5,4)&(5,5)&(5,6) \\ 6 & (6,1) & (6,2) & (6,3) & (6,4)&(6,5)&(6,6) \end{array}
A=दो पासों को फेंकने पर प्राप्त अंक का भिन्न-भिन्न होना
={(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5)}
n(A)=30 \\ P(A)=\frac{30}{36}=\frac{5}{6}
B=दो पासों पर अंकों का योग 4 होने की घटना=\{(1,3),(2,2)(3,1)\} \\ A \cap B=\{(1,3),(3, 1) \\ n(A \cap B)=2, P(A \cap B)=\frac{2}{36}=\frac{1}{18} \\ P\left(\frac{B}{A}\right) =\frac{P(A \cap B)}{P(A)} \\ =\frac{\frac{1}{18}}{\frac{5}{6}} \\ =\frac{1}{18} \times \frac{6}{5} \\ \Rightarrow P\left(\frac{B}{A}\right)=\frac{1}{15}
Example:11.एक बक्से में दस कार्ड 1 से 10 तक अंक लिखकर रखे गए और उन्हें अच्छी तरह मिलाया गया।इस बक्से में से एक कार्ड यादृच्छया निकाला गया।यदि यह ज्ञात हो कि निकाले गए कार्ड पर 3 अंक से अधिक है तो इस अंक के सम होने की क्या प्रायिकता है?
Solution:बक्से में मिलाए गए कार्ड की प्रतिदर्श समष्टि={1,2,3,4,5,6,7,8,9,10}
A=निकाले गए कार्ड पर अंक 3 से अधिक होना= {4,5,6,7,8,9,10}
B=निकाले गए कार्ड पर अंक का सम होना ={4,6,8,10}
n(A)=7, \quad P(A)=\frac{7}{10}, \quad A \cap B=\{4,6,8,10\} \\ P(A \cap B)=\frac{4}{10}=\frac{2}{5} \\ P\left(\frac{B}{A}\right) =\frac{P (A \cap B)}{P(A)} \\ =\frac{\frac{2}{5}}{\frac{7}{10}}=\frac{2}{5} \times \frac{10}{7}=\frac{4}{7} \\ \Rightarrow P\left(\frac{B}{A}\right)=\frac{4}{7}
Example:12.एक विद्यालय में 1000 विद्यार्थी है जिनमें से 430 लड़कियाँ है।यह ज्ञात है कि 430 में से 10% लड़कियाँ कक्षा XII में पढ़ती है।क्या प्रायिकता है कि एक यादृच्छया चुना गया विद्यार्थी कक्षा XII में पढ़ता है यदि यह ज्ञात है कि चुना गया विद्यार्थी लड़की है।
Solution:A=चुना गया विद्यार्थी कक्षा XII में पढ़ता है।
B=चुना गया विद्यार्थी लड़की होना
P(B)= \frac{430}{1000}=\frac{43}{100} \\ P(A \cap B)=\frac{43}{1000} \\ P(\frac{A}{B}) =\frac{P(A \cap B)}{P(B)} \\=\frac{\frac{43}{1000}}{\frac{43}{100}} \\=\frac{43}{1000} \times \frac{100}{43} \\ \Rightarrow P(\frac{A}{B}) =\frac{1}{10}=0.1
Example:13.एक पासे को दो बार उछाला गया है तथा प्रकट हुए अंकों का योग 6 पाया गया।अंक 4 के कम से कम एक बार प्रकट होने की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए।
Solution:A=अंक 4 के कम से कम एक बार प्रकट होना
={(1,4),(4,1),(2,4),(4,2),(3,4),(4,3),(4,4),(5,4),(4,5),(6,4),(4,6)}
B=अंकों का योग 6 होना
={(1,5),(5,1),(2,4),(4,2),(3,3)}
A \cap B=\{(2,4),(4,2)\} \\ n(B)=5, P(B)=\frac{5}{36} \\ n(A \cap B)=\frac{2}{36}=\frac{1}{18} \\ \Rightarrow P(\frac{A}{B})=\frac{P(A \cap B)}{P(B)} \\ =\frac{\frac{1}{18}}{\frac{5}{36}}=\frac{2}{5} \\ \Rightarrow P(\frac{A}{B})=\frac{2}{5}
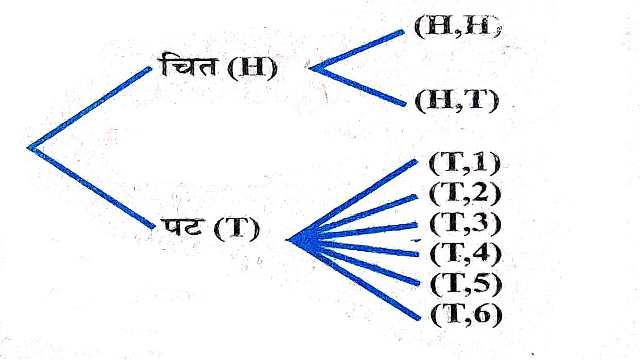
Example:14.एक सिक्के को उछालने के परीक्षण पर विचार कीजिए।यदि सिक्के पर चित्त प्रकट हो तो सिक्के को पुनः उछाले परन्तु सिक्के पर पट प्रकट हो तो एक पासे को फेंके।यदि घटना ‘कम से कम एक पट प्रकट होना’ का घटित होना दिया गया है तो घटना ‘पासे पर 4 से बड़ा अंक प्रकट होना’ की सप्रतिबन्ध प्रायिकता ज्ञात कीजिए।
Solution:परीक्षण का प्रतिदर्श समष्टि है:
S={(H,H),(H,T),(T,1),(T,2),(T,3),(T,4),(T,5),(T,6)}
जहाँ (H,H) दर्शाता है कि दोनों उछाल पर चित्त प्रकट हुआ तथा (T,i) दर्शाता है कि पहली उछाल पट प्रकट हुआ और पासे को फेंकने पर संख्या i प्रकट हुई।
अतः 8 मौलिक घटनाओं (H,H),(H,T),(T,1),(T,2),(T,3),(T,4),(T,5),(T,6) की क्रमशः \frac{1}{4},\frac{1}{4} ,\frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12}, \frac{1}{12} \frac{1}{12} प्रायिकता निर्धारित की जा सकती है।
मान लें F घटना न्यूनतम एक प्रकट होना और E घटना ‘पासे पर 4 से बड़ी संख्या प्रकट होना’ को दर्शाते हैं।
तब F={(H,T),(T,1),(T,2),(T,3),(T,4),(T,5),(T,6)}
E={(T,5),(T,6)}
और E \cap F=\{(T,5),(T,6)\}
अब P(F)=P({(H,T)})+P({(T,1)})+P({(T,2)})+P({(T,3)})+P({(T,4)})+P({(T,5)})+P({(T,6)})
=\frac{1}{4}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{4}
और P(E \cap F)=P(\{T, 5\})+P (\{(T, 6)\})=\frac{1}{12}+\frac{1}{12}=\frac{1}{6}
अतः P(\frac{E}{F})=\frac{P(E \cap F)}{P(F)}=\frac{\frac{1}{6}}{\frac{3}{4}}=\frac{2}{9}
उपर्युक्त उदाहरणों के द्वारा सप्रतिबन्ध प्रायिकता (Conditional Probability),सप्रतिबन्ध प्रायिकता सूत्र (Conditional Probability Formula) को समझ सकते हैं।
3.सप्रतिबन्ध प्रायिकता की समस्याएं (Conditional Probability Problems):
(1.)यदि P(A)=\frac{6}{11} ,P(B)=\frac{5}{11} और P(A \cup B)=\frac{7}{11} हो तो ज्ञात कीजिए।
\text { (i) } P(A \cap B) \text { (ii) } P(\frac{A}{B}) \text { (iii) } P(\frac{B}{A})
(2.)एक प्रशिक्षक के पास 300 सत्य और असत्य प्रकार के आसान प्रश्न,200 सत्य/असत्य प्रकार के कठिन प्रश्न,500 बहुविकल्पीय प्रकार के आसान प्रश्न तथा 400 बहु-विकल्पीय प्रकार के कठिन प्रश्नों का संग्रह है।यदि प्रश्नों के संग्रह में से एक प्रश्न यादृच्छया चुना जाए तो इस प्रश्न के आसान होने की प्रायिकता ज्ञात कीजिए यदि यह ज्ञात है कि यह प्रश्न बहु-विकल्पीय प्रश्न है?
(3.)एक पासे को तीन बार उछाला गया है इस प्रयोग से सम्बन्धित घटनाओं A व B को निम्न प्रकार परिभाषित किया गया है:
A:तीसरी उछाल पर अंक 4 का प्रकट होना,
B:पहली दो उछालों पर क्रमशः 6 तथा 5 प्रकट होना।
उत्तर (Answers):\text { (1) } P(A \cap B)=\frac{4}{11}, P(\frac{A}{B})=\frac{4}{5} ,P(\frac{B}{A})=\frac{2}{3} \\ \text { (2.) } P(\frac{A}{B})=\frac{5}{9} \\ \text { (3) } P(\frac{A}{B})=\frac{1}{6}
उदाहरण के साथ सशर्त संभाव्यता क्या है?
उपर्युक्त सवालों को हल करने पर सप्रतिबन्ध प्रायिकता (Conditional Probability),सप्रतिबन्ध प्रायिकता सूत्र (Conditional Probability Formula) को ठीक से समझ सकते हैं।
Also Read This Article:-Definite Integral
4.सप्रतिबन्ध प्रायिकता (Conditional Probability),सप्रतिबन्ध प्रायिकता सूत्र (Conditional Probability Formula) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.उदाहरण सहित सप्रतिबन्ध प्रायिकता क्या है? (What is conditional probability with example?):
उत्तर:सशर्त प्रायिकता: P(\frac{A}{B}) घटना A के घटित होने की प्रायिकता है,यह देखते हुए कि घटना B घटित होती है।उदाहरण: यह देखते हुए कि आपने एक लाल कार्ड निकाला है,इसकी क्या प्रायिकता है कि यह पत्ता चौकी (P(\frac{\text{Four}}{\text{Red}}))=\frac{2}{26}=\frac{1}{13} है।तो 26 लाल कार्डों में से (एक लाल कार्ड दिया गया),दो चौके हैं इसलिए \frac{2}{26}=\frac{1}{13}
प्रश्न:2.एक सशर्त प्रायिकता कथन क्या है? (What is a conditional probability statement?):
उत्तर:किसी घटना B की सशर्त प्रायिकता वह प्रायिकता है जिसके घटित होने की प्रायिकता यह जानकर कि एक घटना A पहले ही घटित हो चुकी है।इस प्रायिकता को P(\frac{B}{A}) लिखा जाता है,B दिए गए A की प्रायिकता के लिए प्रदर्शन (notation) है।
प्रश्न:3.आप सशर्त संभाव्यता समस्याओं को कैसे हल करते हैं? (How do you solve conditional probability problems?):
उत्तर:किसी घटना की सशर्त प्रायिकता का सूत्र गुणन नियम 2 से निम्नानुसार प्राप्त किया जा सकता है:
गुणन नियम 2 से प्रारंभ करें।
समीकरण के दोनों पक्षों को P(A) से भाग दें।
समीकरण के दाईं ओर P(A)s को रद्द करें।
समीकरण को कम्यूट करें (Commute the equation)।
हमने सशर्त प्रायिकता का सूत्र निकाला है।
प्रश्न:4.संभाव्यता और सशर्त संभाव्यता के बीच अंतर क्या है? (What is the difference between probability and conditional probability?):
उत्तर:P(A∩B) और P(\frac{A}{B}) बहुत निकट से संबंधित हैं।उनका एकमात्र अंतर यह है कि सशर्त प्रायिकता मानती है कि हम पहले से ही कुछ जानते हैं कि B सत्य है।
P(\frac{A}{B}) के लिए,हालांकि,हम 0 और 1 के बीच एक प्रायिकता प्राप्त करेंगे,यदि A घटित नहीं हो सकता है जब B सत्य है और P(B) यदि A हमेशा सत्य है जब B सत्य है।
प्रश्न:5.क्या बेयस प्रमेय सशर्त प्रायिकता है? (Is Bayes theorem conditional probability?):
उत्तर:बेयस प्रमेय (Bayes’ theorem) जिसका नाम 18वीं सदी के ब्रिटिश गणितज्ञ थॉमस बेयस (British Thomas Bayes) के नाम पर रखा गया है,सशर्त प्रायिकता निर्धारित करने के लिए एक गणितीय सूत्र है।सशर्त प्रायिकता पिछले परिणाम (outcome) के आधार पर होने वाले परिणाम की संभावना है।
प्रश्न:6.हमें सशर्त संभाव्यता की आवश्यकता क्यों है? (Why do we need conditional probability?):
उत्तर:अक्सर कुछ ही संभावित वर्ग या परिणाम होते हैं।किसी दिए गए वर्गीकरण के लिए,कोई अलग-अलग सबूत या पैटर्न प्राप्त करने की संभावना को मापने का प्रयास करता है।
बेयस नियम का उपयोग करते हुए,हम इसका उपयोग वांछित प्राप्त करने के लिए करते हैं, वर्गीकरण की सशर्त प्रायिकता को प्रमाण दिया जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सप्रतिबन्ध प्रायिकता (Conditional Probability),सप्रतिबन्ध प्रायिकता सूत्र (Conditional Probability Formula) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
Conditional Probability
सप्रतिबन्ध प्रायिकता (Conditional Probability)
Conditional Probability
सप्रतिबन्ध प्रायिकता (Conditional Probability) का अध्ययन करने से पूर्व समसंभाव्य परिणामों
की अवस्था में प्रायिकता के अभिगृहीत दृष्टिकोण तथा चिरसम्मत सिद्धान्त का अध्ययन करना आवश्यक है।