Concept of Relations and Functions
1.सम्बन्ध और फलन की संकल्पना (Concept of Relations and Functions),सम्बन्ध और फलन कक्षा 11 (Relations and Functions Class 11):
- सम्बन्ध और फलन की संकल्पना (Concept of Relations and Functions) में संबंध और फलन का अर्थ साधरण व्यक्ति के अनुसार कुछ ओर अर्थ होता है जबकि गणित में इसका कुछ अलग अर्थ होता है।
- साधारण अर्थ में फलन किसी व्यक्ति या वस्तु की एक विशेष गतिविधि या उद्देश्य जिसे पूरा करने या निष्पादित करने के लिए किया जाता है।जैसे दिल का कार्य (Function) शरीर के माध्यम से रक्त पम्प (Pump) करना हैं।
- सम्बन्ध का साधारण अर्थ है जिस तरह से दो लोग, समूह या देश एक-दूसरे के प्रति व्यवहार करते हैं या एक-दूसरे के साथ व्यवहार करते हैं।जैसे राजनयिक सम्बन्ध (Diplomatic Relation),अन्तर्राष्ट्रीय सम्बन्ध (International Relation),विदेशी सम्बन्ध (Foreign Relation) इत्यादि।
- साधारण व्यक्ति को ‘संबंध’ शब्द से कोई गणितीय बोध नहीं होता है।वह समझता है कि ‘अमुक उसकी माता है’,’अमुक उसकी बहिन है’,अमुक उसका सहपाठी है’ इत्यादि।ये सभी दो व्यक्तियों में,दो संख्याओं में या समुच्चय के दो अवयवों में सम्बन्ध प्रकट करते हैं।इस प्रकार के संबंधों को द्विचर सम्बन्ध कहते हैं।इनके अलावा अन्य प्रकार के संबंध होते हैं जैसे:’कोई संख्या स्वयं का वर्ग है’,’ कोई स्वयं की दुगनी है’ इत्यादि।सामान्य भाषा में संबंध से हमारा तात्पर्य है:’एक वस्तु का दूसरी से किसी नियम से संबंधित होना’।जैसे परस्पर लंब होना।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Set Theory Functions
2.फलन की संकल्पना की ऐतिहासिक पृष्ठभूमि (Historical Background of Concept of Functions):
- फलन की संकल्पना R. Descartes (सन् 1596-1650 ई.) से प्रारंभ होकर एक लंबे अंतराल में विकसित हुई।Descartes ने सन् 1637 ईस्वी में अपनी पांडुलिपि “Geometric” में शब्द ‘फलन’ का प्रयोग ज्यामितीय वक्रों जैसे अतिपरवलय (Hyperbola),परवलय (Parobola) तथा दीर्घवृत (Ellipse) का अध्ययन करते समय एक चर राशि x के धन पूर्णांक घात x^n के अर्थ में किया था।जेम्स ग्रेगरी (James Gregory) (सन् 1636-1675 ईस्वी) ने अपनी कृति “Vera Circuliet Hyperbolae Quadratura” (सन् 1667 ईस्वी) में फलन को एक ऐसी राशि माना था जो किसी अन्य राशि पर बीजीय अथवा अन्य संक्रियाओं को उत्तरोत्तर प्रयोग करने से प्राप्त होता है।बाद में जी डब्ल्यू लेबनीज (G.W. Leibnitz) (1646-1716 ईस्वी) ने 1673 ईस्वी में लिखित अपनी पांडुलिपि “Methodus angentium inversa seu de functionibus” में शब्द ‘फलन’ को किसी ऐसी राशि के अर्थ में प्रयोग किया जो किसी वक्र के एक बिन्दु से दूसरे बिन्दु तक इस प्रकार परिवर्तित होती रहतीं है जैसे वक्र के बिन्दु, वक्र की प्रवणता,वक्र की स्पर्शी तथा अभिलंब परिवर्तित होते हैं।तथापि अपनी कृति “हिस्टोरिया (Historia)” (1714 ईस्वी) में लेबनीज (Leibnitz) ने फलन को एक चर पर आधारित राशि के रूप में प्रयोग किया था।
- वाक्यांश ‘x का फलन’ प्रयोग में लाने वाले वे सर्वप्रथम व्यक्ति थे।जाॅन बर्नौली (John Bernoulli) (1667-1748 ईस्वी) ने सर्वप्रथम 1718 ईस्वी में संकेतन (Notation) \phi{x} को वाक्यांश ‘x का फलन’ को प्रकट करने के लिए किया था।परंतु फलन को निरूपित करने के लिए प्रतीकों जैसे f,F,\phi{},\psi{}… का व्यापक प्रयोग लियोनहार्ड यूलर (Leonhard Euler) (1707-1784 ईस्वी) द्वारा 1734 ईस्वी में अपनी पांडुलिपि “Analysis Infinitorium” के प्रथम खंड में किया गया था। बाद में Joeph Lousis Lagrange (1736-1813 ईस्वी) ने 1793 में अपनी पांडुलिपि “Theoriedes functions analytiques” प्रकाशित की जिसमें उन्होंने विश्लेषणात्मक (Analytic) फलन के बारे में परिचर्चा की थी तथा संकेतन f(x),F(x),\phi{(x)} आदि का प्रयोग x के भिन्न-भिन्न फलनों के लिए किया था।तदोपरांत Lejeunne Dirichlet (1805-1895 ईस्वी) ने फलन की परिभाषा दी।जिसका प्रयोग उस समय तक होता रहा जब तक वर्तमान काल में फलन की सैद्धांतिक परिभाषा का प्रचलन नहीं हुआ जो जाॅर्ज केन्टर (Georg Cantor) (1845-1918 ईस्वी) द्वारा विकसित समुच्चय सिद्धांत के बाद हुआ।वर्तमान काल में प्रचलित फलन की समुच्चय सैद्धान्तिक परिभाषा Drichlet द्वारा प्रदत्त फलन की परिभाषा का मात्र अमूर्तीकरण (Abstraction) है।
Also Read This Article:continuity of functions of 2 variables
3.संबंध और फलन (Relations and Functions):
- समुच्चय की संकल्पना की भाँति फलन की संकल्पना भी एक लंबे समय के अंतराल में विकसित हुई।जैसा ऊपर वर्णित किया गया है कि आर. डेकार्टेज (R. Descartes) (1596-1650) ने प्रथम बार शब्द फलन का उपयोग किया।जेम्स ग्रेगरी (James Gregory) (1638-1875) ने फलन को अन्य संक्रियाओं से प्राप्त राशि के रूप में परिभाषित किया जो वर्तमान में परिभाषा प्रचलित है उसका विकास जॉर्ज कैंटर (George Cantor) ने किया।’Function’ एक लैटिन शब्द है जिसका अर्थ ‘संक्रिया’ से व्युत्पन्न है।यदि हम एक पूर्णांक x को दुगुना करते हैं तो हम सोचते हैं कि एक समपूर्णांक पाने के लिए संक्रिया की गई है।इसलिए हम फलन को एक नियम के रूप में देखते हैं जिससे कुछ दी हुई संख्याओं से नई संख्याएं उत्पन्न होती है।फलन को निरूपित करने के लिए अनेक पद जैसे प्रतिचित्र,प्रतिचित्रण का प्रयोग करते हैं।हम विभिन्न प्रकार के फलनों यथा एकैकी (one-to-one function or injective function),आच्छादक (onto or surjective),अन्तर्क्षेपी (into),एकैकी अन्तर्क्षेपी (one-one into),बहुएकी आच्छादक (Many one onto),तत्समक फलन और अचर फलन का अध्ययन करते हैं।
- फलन की परिभाषा (Definition of a Function):यदि समुच्चय X का प्रत्येक अवयव (element) किसी नियम f द्वारा समुच्चय Y के एक अद्वितीय (unique) अवयव से संबद्ध होता है नियम f को समुच्चय A से B में एक फलन या प्रतिचित्रण (mapping) कहते हैं:
f:X\rightarrow{Y} - यदि समुच्चय X का अवयव x,समुच्चय Y अवयव y से सम्बद्ध होता है (नियम f द्वारा) तो (x,y) के क्रमित युग्मों (Ordered Pairs) का समुच्चय ही फलन f है।अवयव y को अवयव x का f-प्रतिबिंब (f-image) कहते हैं जिसे निम्न प्रकार दर्शाते हैं:
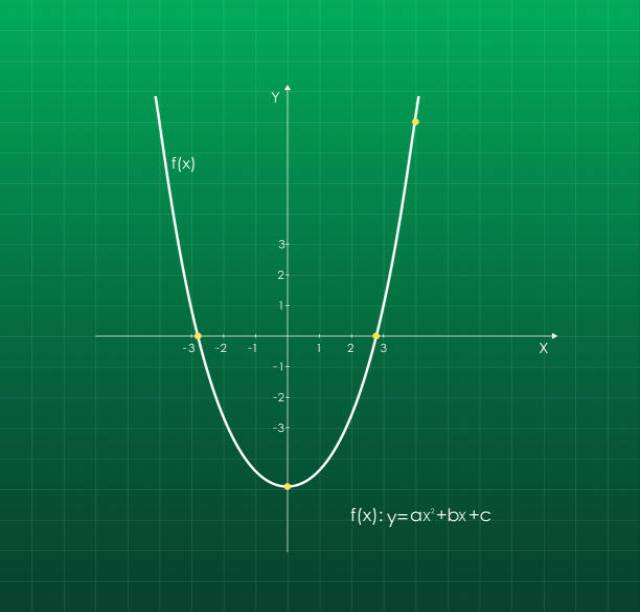
y=f(x) \text{ या }f:x\rightarrow{y} - उदाहरण:y=x अथवा y=2x अथवा y=\frac{x}{2} \text{ अथवा }y=x^2+1 इन समस्त समीकरणों में x का मान निर्धारित करने से y का मान ज्ञात किया जा सकता है।यह भी संभव है कि y स्पष्ट रूप से x के पदों में न दिया गया हो बल्कि x और y का संबंध किसी ज्यामितीय रचना द्वारा व्यक्त किया गया हो जिससे हम फलन का निर्धारण कर सकें।
- ऐसी परिस्थितियों में हम कहते हैं कि y चर x का फलन (function) है।एक चर दूसरे चर पर फलनीय परतन्त्रता ही शायद उच्च गणित के समस्त क्षेत्र की सबसे महत्त्वपूर्ण संकल्पना है।फलन के गुणधर्म:
(1.)x के प्रत्येक मान के लिए y सुनिश्चित है।
(2.)x के प्रत्येक मान के लिए जिसके लिए y निर्धारित है,y का एक और केवल एक ही मान होता है।
(3.)x और y का पारस्परिक सम्बन्ध एक वैश्लेषिक सूत्र द्वारा दिया गया है जिससे x के किसी दिए हुए मान के लिए y का मान प्रत्यक्ष x का मान रखकर निकाला जा सकता है। - उपर्युक्त आर्टिकल में सम्बन्ध और फलन की संकल्पना (Concept of Relations and Functions),सम्बन्ध और फलन कक्षा 11 (Relations and Functions Class 11) के सम्बन्ध में बताया गया है।
4.अजीब मेहनती स्टूडेन्ट (हास्य-व्यंग्य) (Wonderful Laborious Student):
- पिताजी (कर्मठ बेटे से):तुम्हारी गणित की तैयारी कैसी है?
- कर्मठ:पिताजी!बहुत अच्छी तैयारी कर रहा हूं।
- पिताजी:गणित में बहुत कठिन परिश्रम करने की जरूरत होती है।
- कर्मठ:कठिन परिश्रम तो मैं इतना करता हूं कि मैं अपना गणित का गृहकार्य को समाप्त करके अन्य सहपाठियों के गृहकार्य में भी मदद कर देता हूं।
- पिताजी:वो कैसे?
- कर्मठ:गुरुजी जो गणित में गृहकार्य बताते हैं उसके हल पासबुक से नकल करके लिख देता हूं;अपनी गृहकार्य की नोटबुक में भी और सहपाठियों की नोटबुक में भी।
इसके अलावा कक्षा में गुरुजी कोई भी सवाल हल करने के लिए देते हैं।सभी छात्र-छात्राएं सवाल हल करके दे देते हैं परंतु मैं सवाल को अंतिम समय तक हल करने के लिए कठिन परिश्रम करता रहता हूँ। - पिताजी:अंत में सवाल को हल कर पाते हो या नहीं।
कर्मठ:अंत में गुरुजी मेरे पास आकर कहते हैं कि सबने सवाल हल कर दिए हैं पर तुमने अभी तक नहीं किया। - कर्मठ:मैं कोशिश कर रहा हूं।तब गुरुजी कहते हैं कि अब तुम भी कैसे भी हो,किसी भी तरह हो,जैसा भी हो सवाल को हल करके तुरंत दो।
गुरुजी के जाते ही मैं पासबुक निकालकर सवाल का हल नोटबुक में उतार कर गुरुजी को दिखा देता हूं फिर गुरु जी कहते हैं: - गुरुजी:वाह कर्मठ! तुम तो इतने ईमानदार,शालीन और यथा नाम तथा गुण भी हो।तुम्हारे अंदर तो कर्मठता कूट-कूट कर भरी हुई है।
5.सम्बन्ध और फलन की संकल्पना (Concept of Relations and Functions),सम्बन्ध और फलन कक्षा 11 (Relations and Functions Class 11) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.फलनों का वर्गीकरण करो।(Classification the functions):
उत्तर:(i)बीजीय फलन (Algebraic Functions):
जिन फलनों के नियम चर के पदों के योग अंतर,अन्तर, गुणा या घात से मिलकर बनते हैं, बीजीय फलन कहलाते हैं।जैसे: 2x^{3}+7x^{2}+9x+3 [बहुपद फलन (Polynomial)]
(ii)अबीजीय फलन (Non-Algebraic or Transcendental functions):
जो फलन बीजीय नहीं होते उन्हें अबीजीय फलन कहते हैं।जैसे:f(x)=e^{x},f(x)=\log{x},f(x)=\sec{x} इत्यादि।
(iii)सम एवं विषम फलन (Even and Odd Functions):
ऐसे फलन f(x) जिनके लिए f(-x)=f(x)होता है सम फलन कहलाते हैं।जैसे f(x)=x^{2},f(x)=\cos{x} इत्यादि।जिन फलनों f(x) के लिए f(-x)=-f(x) होता है विषम फलन कहलाते हैं।जैसे f(x)=x^{3},f(x)=\sin{x} इत्यादि।
(iv)स्पष्ट एवं स्पष्ट फलन (Explicit and Implicit functions):
यदि x एवं y का ऐसा संबंध है कि एक चर को दूसरे में व्यक्त करना संभव है तो ऐसा फलन स्पष्ट फलन कहलाता है।जैसे:y-2x+3।और यदि संबंध ऐसा है कि एक चर को दूसरे में व्यक्त करना संभव नहीं है ऐसा फलन अस्पष्ट फलन कहलाता है।जैसे:x^{7}y^{2}+y^{9}+x+2y-7=0
(v)आवर्ती फलन (Periodic Functions):
यदि एक फलन f(x) को x के वास्तविक मानों के लिए अंतराल में परिभाषित है तो वह आवर्ती फलन कहलाता है यदि ऐसी वास्तविक संख्या c (शून्य नहीं) विद्यमान है कि f(x+c)=f(x) forevery \quad{x}
प्रश्न:2.बहुएकी फलन किसे कहते हैं?(What is a many one into function called?):
उत्तर:फलन f:X\rightarrow{Y} यदि X के अलग-अलग अवयवों के समुच्चय Y में अलग-अलग प्रतिबिम्ब हो अर्थात्
f(a)=f(b)\Rightarrow{a}=b
एवं f(a)\neq{f(b)}\Rightarrow{a}\neq{b}
यदि फलन एकैकी नहीं है तो वह बहुएकी (Many-one) कहलाता है।
प्रश्न:3.अन्तर्क्षेपी फलन किसे कहते है? (What is the into function called?):
उत्तर:फलन f:X\rightarrow{Y} आच्छादक कहलाता है यदि f(X)=Y अर्थात् f का परिसर एवं सहप्रान्त समान है।स्पष्ट है कि आच्छादक फलन के सहप्रान्त में एक भी अवयव ऐसा नहीं होता जो फलन के प्रान्त के किसी न किसी अवयव का प्रतिबिंब न हो।
यदि f:X\rightarrow{Y} आच्छादक नहीं है तो अन्तर्क्षेपी कहलाता है।अर्थात् अन्तर्क्षेपी फलन के सहप्रान्त में कम से कम एक अवयव ऐसा अवश्य विद्यमान है जो फलन के प्रान्त के किसी अवयव का प्रतिबिंब न हो।
उपर्युक्त प्रश्नों के उत्तर द्वारा सम्बन्ध और फलन की संकल्पना (Concept of Relations and Functions),सम्बन्ध और फलन कक्षा 11 (Relations and Functions Class 11) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Concept of Relations and Functions
सम्बन्ध और फलन की संकल्पना
(Concept of Relations and Functions)
Concept of Relations and Functions
सम्बन्ध और फलन की संकल्पना (Concept of Relations and Functions) में संबंध और फलन का अर्थ
साधरण व्यक्ति के अनुसार कुछ ओर अर्थ होता है जबकि गणित में इसका कुछ अलग अर्थ होता है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
