Coefficient of Correlation
1.सहसम्बन्ध गुणांक (Coefficient of Correlation),वर्गीकृत श्रेणी में कार्ल पियर्सन का सहसम्बन्ध गुणांक का परिकलन (Calculation of Karl Pearson Coefficient of Correlation in Grouped Series):
सहसम्बन्ध गुणांक (Coefficient of Correlation) व्यक्तिगत श्रेणी की भाँति वर्गीकृत श्रेणी में भी कार्ल पियर्सन का सहसम्बन्ध गुणांक ज्ञात किया जा सकता है।वर्गीकृत श्रेणी से सहसम्बन्ध गुणांक ज्ञात करने के लिए सहसम्बन्ध सारणी (Correlation Table) की आवश्यकता होती हैं।सहसम्बन्ध सारणी वर्गीकृत समंक श्रेणियों की एक द्वि-चर आवृत्ति सारणी (Bivariate Frequency Table) है।इसमें दो खण्डित या सतत श्रेणियों की कोष्ठ आवृत्तियाँ (Cell Frequencies) तथा कुल आवृत्तियाँ (Total Frequencies) इस प्रकार प्रस्तुत की जाती हैं कि दोनों में अन्तर्सम्बन्ध स्थापित हो सके।इस सारणी के विभिन्न कोष्ठकों (cells) में X व Y श्रेणियों की उभयनिष्ठ (Common) आवृत्तियाँ लिखी जाती हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-KarlPearson Correlation Coefficient
2.सहसम्बन्ध गुणांक के साधित उदाहरण (Coefficient of Correlation Solved Examples):
Example:29.निम्न सारणी में प्रस्तुत समंकों से आयु तथा बीमित राशि में सहसम्बन्ध गुणांक का परिकलन कीजिएः
(Calculate coefficient of correlation between age and the sum assured from the data given in the following table):

Solution:Calculation Table of Karl Pearson Coefficient of Correlation

![Rendered by QuickLaTeX.com r=\frac{N \times \Sigma f d x d y-\left(\Sigma f d x \times \Sigma f d y\right)}{\sqrt{N \times \Sigma f d^2 x-\left(\Sigma f d x\right)^2} \sqrt{N \times \Sigma f d^{2}y-(\Sigma f dy)^2} } \\ =\frac{100(-40)-(-33 \times 39)}{\sqrt{\left[100 \times 131-(-33)^{2}\right]} \sqrt{\left[100 \times 109-(39)^2\right]}} \\ =\frac{-4000+1287}{\sqrt{(13100-1089)} \sqrt{(10900-1521)}} \\ =\frac{-2713}{109.5947 \times 96.8452} \\=\frac{-2713}{10613.72064} \\ =-0.2556 \\ r \approx-0.26](https://www.satyamcoachingcentre.in/wp-content/ql-cache/quicklatex.com-45611eb2bfa7217d0cd17c4bd4ae919c_l3.png)
Example:30.निम्न सारणी वर्गानुसार 66 विद्यार्थियों के एक बुद्धि परीक्षा में प्राप्तांकों की आवृत्ति वितरण को प्रदर्शित करती है।आयु तथा बुद्धि परीक्षा में सहसम्बन्ध की मात्रा (स्तर) का परिकलन कीजिएः
(The following table gives the frequency according to age groups of marks obtained by 66 students in an intelligence test.Measure the degree of relationship between in age and intelligence test):
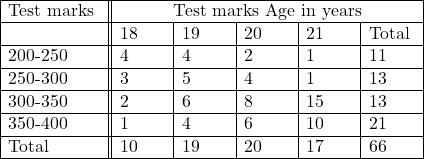
Solution:Calculation Table of Karl Pearson Coefficient of Correlation

![Rendered by QuickLaTeX.com r=\frac{N \times \Sigma f d x d y-\left(\Sigma f d x \times \Sigma f d y\right)}{\sqrt{N \times \Sigma f d^2 x-\left(\Sigma f d x\right)^2} \sqrt{N \times \Sigma f d^{2}y-(\Sigma f dy)^2} } \\ =\frac{66 \times 36-(-22 \times-14)}{\sqrt{\left[66 \times 76-(-22)^2\right]} \sqrt{\left[66 \times 78-(-14)^2\right]}} \\ =\frac{2376-308}{\sqrt{(5016-484)} \sqrt{(5148-196)}} \\ r=\frac{2068}{67.3201 \times 70.3704} \\ =\frac{2068}{4737.342365} \\ =0.436531675 \\ r \approx+0.4365](https://www.satyamcoachingcentre.in/wp-content/ql-cache/quicklatex.com-665b790a225950568388e388f173cc7b_l3.png)
Example:31.निम्न सारणी में 25 परीक्षार्थियों द्वारा अर्थशास्त्र और सांख्यिकी में प्राप्तांक दिए गए हैं।दोनों विषयों के प्राप्तांकों का पारस्परिक सहसम्बन्ध गुणांक परिकलित कीजिएः
(The following table gives the marks obtained by 25 students in Economics and Statistics.Calculate coefficient of correlation between marks obtained in both the subjects):

Solution:Calculation Table of Karl Pearson Coefficient of Correlation

![Rendered by QuickLaTeX.com r=\frac{N \times \Sigma f d x d y-\left(\Sigma f d x \times \Sigma f d y\right)}{\sqrt{N \times \Sigma f d^2 x-\left(\Sigma f d x\right)^2} \sqrt{N \times \Sigma f d^{2}y-(\Sigma f dy)^2} } \\ =25 \times 22-(-18 \times-18) \\ \sqrt{\left[25 \times 38-(-18)^2\right] \sqrt{\left[25 \times 34-(-18)^2\right]}} \\ =\frac{550-324}{\sqrt{(950-324)} \sqrt{(850-324)}} \\ =\frac{226}{\sqrt{626} \sqrt{526}} \\ r=\frac{226}{25.019992 \times 22.934689} \\ =\frac{226}{573 \cdot 8257355} \\ =0.393847 \\ r \approx + 0.394](https://www.satyamcoachingcentre.in/wp-content/ql-cache/quicklatex.com-156b9e9b4ff9e317aa6a305d595e6a4f_l3.png)
Example:32.निम्नलिखित सारणी दो परीक्षाओं में 81 विद्यार्थियों द्वारा 100 में से प्राप्त अंकों को प्रदर्शित करती है।यह बतलाइए कि दोनों परीक्षाओं में प्राप्त अंकों में क्या सहसम्बन्ध है?
(The following table shows the total number of marks obtained out of 100 by 81 students of a certain class in two examinations.Find out whether there is any relationship between the marks obtained in these two examinations.)

Solution:Calculation Table of Karl Pearson Coefficient of Correlation
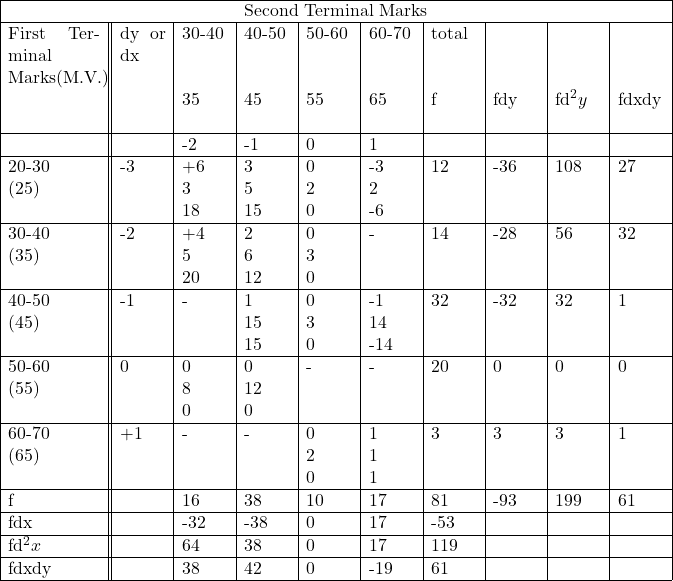
![Rendered by QuickLaTeX.com r=\frac{N \times \Sigma f d x d y-\left(\Sigma f d x \times \Sigma f d y\right)}{\sqrt{N \times \Sigma f d^2 x-\left(\Sigma f d x\right)^2} \sqrt{N \times \Sigma f d^{2}y-(\Sigma f dy)^2} } \\ =\frac{81 \times 61-(-53 \times-93)}{\sqrt{\left[81 \times 119-(-53)^2\right]} \sqrt{\left[81 \times 199-(-93)^2\right]}} \\ =\frac{4941-4929}{\sqrt{(9639-2809) \sqrt{(16119-8649)}}} \\ =\frac{12}{\sqrt{6830} \sqrt{7470}} \\ =\frac{12}{82.6438 \times 86.42916} \\ =\frac{12}{7142.834213} \\ =0.00168005 \\ r \approx+0.00168](https://www.satyamcoachingcentre.in/wp-content/ql-cache/quicklatex.com-cbe79f3fc374c67d7ec60c23909e52a4_l3.png)
Example:33.निम्नलिखित समंकों से कार्ल पियर्सन का सहसम्बन्ध गुणांक ज्ञात कीजिएः
(Calculate Karl Pearson’s Coefficient of Correlation from the following data):

Solution:Calculation Table of Karl Pearson Coefficient of Correlation

![Rendered by QuickLaTeX.com r=\frac{N \times \Sigma f d x d y-\left(\Sigma f d x \times \Sigma f d y\right)}{\sqrt{N \times \Sigma f d^2 x-\left(\Sigma f d x\right)^2} \sqrt{N \times \Sigma f d^{2}y-(\Sigma f dy)^2} } \\ =\frac{15 \times 8-(-1 \times 4)}{\sqrt{\left[15 \times-(-1)^2\right]}\sqrt{\left[15 \times 26-(4)^2\right]}} \\ =\frac{120+4}{\sqrt{(105-1)} \sqrt{390-16}} \\ =\frac{124}{\sqrt{104} \sqrt{374}} \\ =\frac{124}{10.198 \times 19.33907} \\ =\frac{124}{197.2198359} \\ =0.62874 \\ r \approx+0.63](https://www.satyamcoachingcentre.in/wp-content/ql-cache/quicklatex.com-198300a1e28afe8f0994013165dc53cc_l3.png)
Example:34.सांख्यिकी एवं लेखाशास्त्र में विद्यार्थियों द्वारा प्राप्त अंक निम्न कोष्ठकों में प्रस्तुत हैं।प्रथम अंक सांख्यिकी में एवं द्वितीय लेखाशास्त्र मेंः
(14,12),(0,2),(1,5),(7,3),(15,9),(2,8),(12,18),(9,11),(5,3),(17,13),(19,18),(11,7),(10,13),(13,16),(16,14),(6,10),(4,1),(11,14),(8,3),(9,15),(13,11),(14,17),(10,10),(11,7),(15,15)
अंकों का वर्ग विस्तार रखते हुए एक द्वि-चर सारणी बनाइए जिसमें प्रथम वर्गान्तर (0-4) हो,तत्पश्चात सांख्यिकी एवं लेखाशास्त्र में प्राप्तांकों के मध्य सहसम्बन्ध गुणांक की परिगणना कीजिए।
(Taking the class group of each starting with 0-4,prepare a bivariate frequency distribution and thereafter calculate coefficient of correlation on between marks in statistics and accountancy.)

Solution:Bivariate Frequency Distribution Marks in Statistics

Calculation Table of Karl Pearson Coefficient of Correlation
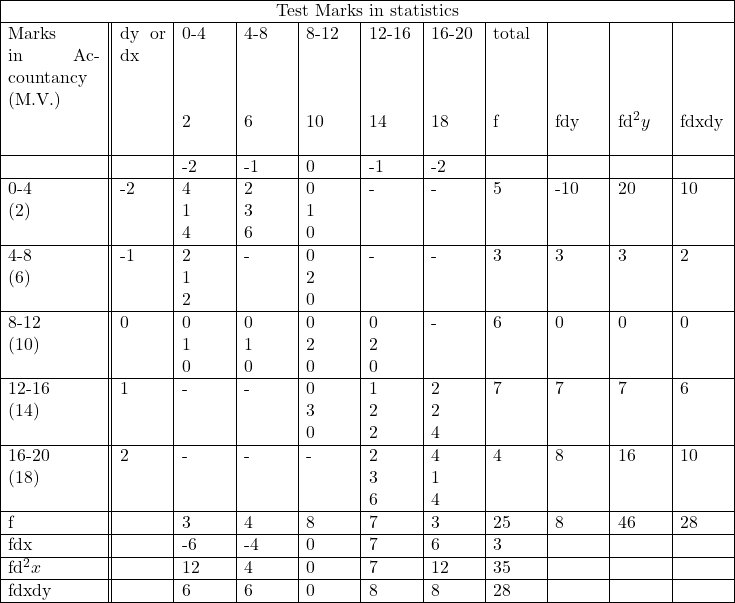
![Rendered by QuickLaTeX.com r=\frac{N \times \Sigma f d x d y-\left(\Sigma f d x \times \Sigma f d y\right)}{\sqrt{N \times \Sigma f d^2 x-\left(\Sigma f d x\right)^2} \sqrt{N \times \Sigma f d^{2}y-(\Sigma f dy)^2} } \\ =\frac{25 \times 28-(3 \times 8)}{\sqrt{\left[25 \times 35-(3)^2\right]} \sqrt{\left[25 \times 46-(8)^2\right]}} \\ =\frac{700-24}{\sqrt{(875-9)}\sqrt{(1150-64)}} \\ =\frac{676}{\sqrt{866 \sqrt{1086}}} \\ =\frac{676}{29.42788 \times 32.95455} \\ =\frac{676}{969.7813657} \\ =0.697064 \\ r \approx+0.6970](https://www.satyamcoachingcentre.in/wp-content/ql-cache/quicklatex.com-298f01f4f36a8e382dab0ff9fbf9ebd8_l3.png)
उपर्युक्त उदाहरणों के द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation),वर्गीकृत श्रेणी में कार्ल पियर्सन का सहसम्बन्ध गुणांक का परिकलन (Calculation of Karl Pearson Coefficient of Correlation in Grouped Series) को समझ सकते हैं।
3.सहसम्बन्ध गुणांक पर आधारित सवाल (Questions Based on Coefficient of Correlation):
(1.)नीचे दिए गए आँकड़ों से कार्ल पियर्सन विधि द्वारा पतियों और पत्नियों की आयु का पारस्परिक सहसम्बन्ध गुणांक ज्ञात कीजिएः
(From the following data,calculate Karl Pearson’s coefficient of correlation between age of husband and wives):

(2.)निम्न सारणी में विद्यार्थियों की ऊँचाई और भार के समंक दिए गए हैं।ऊँचाई और भार में सहसम्बन्ध गुणांक निकालिएः
(The following table gives to figures of height and weight of students.Obtain coefficient of correlation between height and weight):

उत्तर (Answers):(1.)r=+0.79 (2.)r=+0.0944
उपर्युक्त सवालों को हल करने पर सहसम्बन्ध गुणांक (Coefficient of Correlation),वर्गीकृत श्रेणी में कार्ल पियर्सन का सहसम्बन्ध गुणांक का परिकलन (Calculation of Karl Pearson Coefficient of Correlation in Grouped Series) को ठीक से समझ सकते हैं।
Also Read This Article:-KarlPearson Coefficient of Correlation
4.सहसम्बन्ध गुणांक (Frequently Asked Questions Related to Coefficient of Correlation),वर्गीकृत श्रेणी में कार्ल पियर्सन का सहसम्बन्ध गुणांक का परिकलन (Calculation of Karl Pearson Coefficient of Correlation in Grouped Series) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.वर्गीकृत श्रेणी में कार्ल पियर्सन का सहसम्बन्ध गुणांक ज्ञात करने की क्रियाविधि लिखिए। (Write the Working Rule of Karl Pearson’s Coefficient of Correlation in Grouped Series):
उत्तर:(1.)दी हुई द्वि-चर सारणी में चार खाने (Columns) दायीं ओर तथा तीन पंक्तियाँ (Rows) नीचे की ओर बनाई जाती है।दायीं ओर से खाने में प्रथम खाना Y के कल्पित माध्य से ज्ञात किए गए विचलनों (dy) के लिए,द्वितीय व तृतीय खाना fdy तथा fd^{2}y के लिए तथा चतुर्थ खाना fdxdy के लिए बनाया जाता है।इसी प्रकार नीचे की ओर तीन पंक्तियाँ क्रमशः dx,fdx,fd^{2}x व के लिए बनाई जाती है।
(2.)X तथा Y के मध्य-बिन्दुओं (Mid-Values) में से किसी एक मध्य-मूल्य को कल्पित माध्य मानकर विचलन (dx व dy) ज्ञात किए जाते हैं।यदि वर्गान्तर समान हो या मूल्यों में अन्तर समान हो तो उभयनिष्ठ गुणक (Common factor) निकालकर पद-विचलन ज्ञात करना अधिक सरल रहता है।X श्रेणी में पद-विचलन निकालने के लिए X-श्रेणी में वर्ग-विस्तार आपस में समान होने चाहिए।इसी प्रकार Y श्रेणी में पद विचलनों को निकालने के लिए Y-श्रेणी में वर्ग-विस्तार आपस में समान होने चाहिए।X-श्रेणी में यदि 5-5 का तथा Y श्रेणी में यदि 7-7 का या 10-10 का वर्ग विस्तार हो तो भी पद-विचलन रीति का प्रयोग किया जा सकता है।इसी प्रकार किसी एक श्रेणी अर्थात् X या Y में समान वर्ग-विस्तार तथा दूसरे में असमान वर्ग-विस्तार होने पर केवल वर्ग-विस्तार वाली श्रेणी में पद विचलनों का प्रयोग किया जा सकता है।
(3.)दोनों श्रेणियों के विचलनों (dx तथा dy) को सम्बन्धित आवृत्तियों से गुणा करके गुणनफल सम्बन्धित खानों एवं पंक्तियों में लिखे जाते हैं।इन गुणनफलों का योग क्रमशः \Sigma fdy तथा \Sigma fdx होता है।
(4.)fdx को सम्बन्धित dx से गुणा करके इन गुणाओं का योग \Sigma fd^{2}x तथा \Sigma fd^{2}y होता है।
(5.)द्विचर सारणी के जिन-जिन कोष्ठों (cells) में आवृत्तियाँ होती हैं उनके तत्सम्बन्धी dx,dy व f(cell frequency) को आपस में गुणा कर fdxdy ज्ञात कर लिए जाते हैं।यह गुणनफल तृतीय पंक्ति में लिखा जाता है जिसका योग होता है।
(6.)निम्न में से किसी एक सूत्र का प्रयोग किया जाएगाः
प्रथम सूत्रः r=\frac{\Sigma f dx dy \cdot N-\left(\bar{x}-A_x\right)\left(\bar{Y}-A_y\right)}{N \sigma_{x} \sigma_{y}}
सूत्र में प्रयुक्त कोष्ठ आवृत्तियों तथा तत्सम्बन्धी X व Y श्रेणियों के कल्पित माध्य से विचलनों (dx व dy) के गुणनफल के योग से है।अन्य सभी चिन्हों का अर्थ पूर्व-वर्णित सूत्रों के अनुसार ही है।
इस उपर्युक्त सूत्र से अन्य सूत्र ज्ञात किए जा सकते हैं जो निम्न प्रकार हैंः
द्वितीय सूत्रः r=\frac{\Sigma f d x d y-N\left(\frac{\Sigma f d x}{N}\right) \left(\frac{\Sigma f dy}{N} \right)}{N \sqrt{\left[\frac{\Sigma f d^2 x}{N}-\left(\frac{\Sigma f dx}{N}\right)^2\right]} \sqrt{\left[\frac{\Sigma f d^2 y}{N}-\left(\frac{\Sigma f dy}{N}\right)^2\right]}}
तृतीय सूत्रः r=\frac{\Sigma f d x d y-\frac{\Sigma f d x \cdot \Sigma f dy}{N}}{\sqrt{\left[\Sigma f d^2 x-\left(\frac{\Sigma f dx}{N}\right)^{2}\right]\left[\Sigma f d^2 y-\left(\frac{\Sigma f dy}{N}\right)^{2}\right]}}
चतुर्थ सूत्रः r=\frac{N \cdot \Sigma f d x d y-\Sigma f d x \cdot \Sigma f dy}{\sqrt{\left[N \times \Sigma f d^2 x-(\Sigma f dx)^2\right]\left[N \times \Sigma f d^2y-(\Sigma f dy)^2\right]}}
प्रश्न:2.सम्भाव्य विभ्रम की उपयोगिता क्या है? (What is the Utility of Probable Error?):
उत्तर:सम्भाव्य विभम्र के प्रमुखतः निम्न दो उपयोग हैंः
(1.)सीमा निर्धारण (Determination of Limits):सहसंबंध गुणांक की सम्भाव्य विभम्र के माध्यम से दो सीमाएँ (r \pm P.E.)ज्ञात हो जाती है जिनमें अन्य दैव प्रतिदर्शों के निकाले गए या संपूर्ण समग्र के आधार पर निकाले गए सहसंबंध गुणांक के पाए जाने की 50% संभावना होती है।
(2.)सहसंबंध गुणांक का निर्वचन (Interpretation of Coefficient of Correlation):संभाव्य विभ्रम के आधार पर कार्ल पियर्सन के सहसंबंध गुणांक का निर्वाचन निम्न नियमों के अनुसार किया जाता हैः
(i) यदि सहसंबंध गुणांक सम्भाव्य विभम्र से कम है (r<6 P.E.)तो दोनों श्रेणियों में सहसंबंध सार्थक (significant) या अर्थपूर्ण होता है।दूसरे शब्दों में सहसम्बन्ध गुणांक के सम्भाव्य विभम्र के छः गुने से अधिक होने पर यह कहा जा सकता है कि दोनों श्रेणियों में सहसंबंध निश्चित रूप से विद्यमान है।सहसम्बन्ध सम्भाव्य विभम्र के छः गुने से जितना अधिक होगा वह उतना ही अधिक सार्थक या अर्थपूर्ण होगा।यदि सहसंबंध गुणांक सम्भाव्य विभम्र के छः गुने से अधिक नहीं है (r>6 P.E.) तो सहसम्बन्ध अधिक नहीं माना जाता है।
(iii)यदि सहसम्बन्ध गुणांक 0.3 से भी कम है ताकि इसका संभाव्य विभ्रम अपेक्षाकृत कम है तो सहसम्बन्ध की मात्रा नगण्य (Not marked) समझनी चाहिए।
(iv)यदि सहसम्बन्ध गुणांक +0.5 या अधिक है तो सहसम्बन्ध का अस्तित्व लगभग निश्चित समझना चाहिए।
उपर्युक्त नियमों को ध्यान में रखते हुए ही सहसंबंध गुणांक एवं संभाव्य विभ्रम के संबंध का अध्ययन करके यह निष्कर्ष निकालना चाहिए कि सहसंबंध अर्थपूर्ण है अथवा नहीं।
प्रश्न:3.सम्भाव्य विभ्रम की परिसीमाएं क्या हैं? (What are Limitations of Probable Error?):
उत्तर:सम्भाव्य विभ्रम की परिसीमाएं (Limitations of Probable Error):संभाव्य विभ्रम का प्रयोग केवल निम्नलिखित परिस्थितियों में उचित रहता हैः
(1.)जब पद-युग्मों की संख्या पर्याप्त हो
(2.) जब सहसंबंध गुणांक दैव प्रतिचयन के आधार पर चुने गए मूल्य से ज्ञात किया गया है तथा
(3.)श्रेणी सममित अर्थात् प्रसामान्य (symmetrical) हो।
आर्थिक सामाजिक एवं व्यवसायिक क्षेत्रों में अधिकतर उपर्युक्त परिस्थितियां पूरी नहीं होती।इन क्षेत्रों में सम्भाव्य विभम्र का प्रयोग उचित नहीं समझा जाता है।इसके अतिरिक्त सम्भाव्य विभम्र के माध्यम से सहसंबंध गुणांक की 50% उपस्थिति की सम्भावना ही निश्चित होती है,अतः “यह न तो विभ्रम है और न पूर्णरूप से सम्भाव्य ही है।”
प्रश्न:4.प्रमाप विभ्रम ज्ञात करने के सूत्र को समझाइए। (Explain the Formula of Standard Error):
उत्तर:प्रमाप विभ्रम (Standard Error)
चूँकि सम्भाव्य विभ्रम सहसंबंध गुणांक की 50% संभावना की सीमा ही निर्धारित करती है तथा व्यावसायिक एवं सामाजिक क्षेत्रों में इसका प्रयोग उचित नहीं समझा जाता है।आशुनिक सांख्यिकी में सम्भाव्य विभम्र के स्थान पर प्रभाप विभ्रम का प्रयोग उचित समझा जाता है।प्रमाप विभ्रम सम्भाव्य विभ्रम का लगभग \frac{3}{2} होता है।
सूत्रानुसारः r=\frac{1-r^{2}}{N}
प्रतिदर्श (sample) के आधार पर सहसम्बन्ध गुणांक की सम्पूर्ण समग्र के लिए सीमायें निर्धारित करने के लिए निम्न सूत्र का प्रयोग किया जाता हैः
r \pm 3 S.E.of r
यदि प्रतिदर्श छोटा हो तो सम्भाव्य विभम्र तथा प्रमाप विभ्रम की सार्थकता सही जाँच नहीं की जा सकती।बड़े प्रतिदर्श में ही इसका प्रयोग उचित समझा जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सहसम्बन्ध गुणांक (Coefficient of Correlation),वर्गीकृत श्रेणी में कार्ल पियर्सन का सहसम्बन्ध गुणांक का परिकलन (Calculation of Karl Pearson Coefficient of Correlation in Grouped Series) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Coefficient of Correlation
सहसम्बन्ध गुणांक (Coefficient of Correlation)
Coefficient of Correlation
सहसम्बन्ध गुणांक (Coefficient of Correlation) व्यक्तिगत श्रेणी की भाँति वर्गीकृत
श्रेणी में भी कार्ल पियर्सन का सहसम्बन्ध गुणांक ज्ञात किया जा सकता है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








