Circle Class 9
1.वृत्त कक्षा 9 (Circle Class 9),जीवा द्वारा एक बिन्दु पर अन्तरित कोण (Angle Subtended by Chord to a Point):
वृत्त कक्षा 9 (Circle Class 9) के इस आर्टिकल में वृत्त,जीवा द्वारा एक बिन्दु पर अन्तरित कोण तथा तीन बिन्दुओं से जाने वाले वृत्त के बारे में अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Area of Triangles Class 9
2.वृत्त कक्षा 9 पर आधारित उदाहरण (Examples Based on Circle Class 9):
Exercise 10.1
Example:1.खाली स्थान भरिए।
(i)वृत्त का केन्द्र वृत्त के…….. में स्थित है (बहिर्भाग/अभ्यंतर)
(ii)एक बिन्दु,जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो,वृत्त के…….. में स्थित होता है (बहिर्भाग/अभ्यंतर)
(iii)वृत्त की सबसे बड़ी जीवा वृत्त का….. होता है।
(iv)एक चाप……..होता है,जब इसके सिरे एक व्यास के सिरे हों।
(v)वृत्तखण्ड एक चाप तथा…… के बीच का भाग होता है।
(vi)एक वृत्त,जिस तल पर स्थित है,उसे….. भागों में विभाजित करता है।
Solution:(i)अभ्यंतर (ii)बहिर्भाग (iii)व्यास (vi)अर्द्धवृत्त (v)जीवा (vi)तीन
Example:2.लिखिए,सत्य या असत्य
(i)केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखण्ड वृत्त की त्रिज्या होती है।
(ii)एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं।
(iii)यदि एक वृत्त को तीन बराबर भागों में बाँट दिया जाए,तो प्रत्येक भाग दीर्घ चाप होता है।
(iv)वृत्त की जीवा,जिसकी लम्बाई त्रिज्या से दो गुनी हो,वृत्त का व्यास है।
(v)त्रिज्यखण्ड,जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
(vi)वृत्त एक समतल आकृति है।
Solution:(i)सत्य (ii)असत्य (iii)असत्य (iv)सत्य (v)असत्य (vi)सत्य
3.जीवा द्वारा एक बिन्दु पर अन्तरित कोण (Angle Subtended by Chord to a Point):
प्रमेय (Theorem):10.1.वृत्त की बराबर जीवाएँ केन्द्र पर बराबर कोण अन्तरित करती हैं।
दिया है (Given):एक वृत्त,जिसका केन्द्र O है।जीवा AB=जीवा CD
सिद्ध करना है (To Prove):\angle AOB=\angle COD
उपपत्ति (Proof): \triangle OAB और \triangle OCD में
OC=OC (एक ही वृत्त की त्रिज्याएँ)
OB=OD (एक ही वृत्त की त्रिज्याएँ)
AB=CD (दिया है)
SSS सर्वांगसमता गुणधर्म से
\triangle AOB \approx \triangle COD
अतः \angle AOB=\angle COD (CPCT से)
प्रमेय (Theorem):10.2.यदि एक वृत्त की जीवाओं द्वारा केन्द्र पर अन्तरित कोण बराबर हों तो वे जीवाएँ बराबर होती है।
दिया है (Given):एक वृत्त जिसका केन्द्र O है और \angle AOB=\angle COD
सिद्ध करना है (To Prove):AB=CD
उपपत्ति (Proof): \triangle OAB और \triangle OCD में
OA=OA (एक ही वृत्त की त्रिज्याएँ)
\angle AOB=\angle COD (दिया है)
OB=OC (एक ही वृत्त की त्रिज्याएँ)
SAS सर्वांगसमता गुणधर्म से
AB=CD (CPCT से)
\angle OCA =\angle OCB (CPCT से)
परन्तु \angle OCA+\angle OCB=180^{\circ} (रैखिक कोण युग्म से)
\therefore 2 \angle OCA=180^{\circ} \\ \Rightarrow \angle OCA=90^{\circ} \\ \Rightarrow OC \perp AB
Exercise 10.2
Example:1.याद कीजिए कि दो वृत्त सर्वांगसम होते हैं,यदि इनकी त्रिज्याएँ बराबर हों।सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करती है।
Solution:दिया है (Given):दो सर्वांगसम वृत्त जिनके केन्द्र A और B और जीवा PQ=जीवा RS
सिद्ध करना है (To Prove):\angle PAQ=\angle RBS
उपपत्ति (Proof): \triangle APQ और \triangle BRS में
PQ=RS (दिया है)
AP=BR (एक ही वृत्त की त्रिज्याएँ)
AQ=BS (एक ही वृत्त की त्रिज्याएँ)
SSS सर्वांगसमता गुणधर्म से
\triangle APQ \cong \triangle BRS \\ \angle P A Q=\angle RBS (CPCT से)
Example:2.सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करें तो जीवाएँ बराबर होती है।
Solution:दिया है (Given):दो सर्वांगसम वृत्त जिनके केन्द्र A और B हैं।दो जीवाएँ PQ और RS इस प्रकार हैं कि \angle PAQ=\angle RBS
सिद्ध करना है (To Prove):जीवा PQ=जीवा RS
उपपत्ति (Proof): \triangle PAQ और \triangle RBS में
\angle PAQ=\angle RBS (दिया है)
AP=BR (एक ही वृत्त की त्रिज्याएँ)
AQ=BS (एक ही वृत्त की त्रिज्याएँ)
SAS सर्वांगसमता गुणधर्म से
\triangle PAQ \cong \triangle RBS
PQ=RS (CPCT से)
4.केन्द्र से जीवा पर लम्ब (Perpendicular on Chord from Centre):
प्रमेय (Theorem):10.3.एक वृत्त के केन्द्र से एक जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।
Solution:दिया है (Given):एक वृत्त, जिसका केन्द्र O है।AB एक जीवा है और OC \perp AB
सिद्ध करना है (To Prove):AC=BC
रचना (Construction):OA और OB को मिलाया।
उपपत्ति (Proof): \triangle OCA और \triangle OCB में
OA=OB (एक ही वृत्त की त्रिज्याएँ)
OC=OC (उभयनिष्ठ भुजा)
\angle OCA=\angle OCB=90^{\circ} (दिया है)
RHS सर्वांगसमता गुणधर्म से
\triangle OCA \cong \triangle OCB
AB=BC (CPCT से)
प्रमेय (Theorem):10.4.एक वृत्त के केन्द्र से एक जीवा को समद्विभाजित करने के लिए खींची गई रेखा जीवा पर लम्ब होती है।
Solution:दिया है (Given):एक वृत्त जिसका केन्द्र O है।AB एक जीवा है और इसका मध्य-बिन्दु C है।OC को मिलाया गया है।
सिद्ध करना है (To Prove): OC \perp AB
रचना (Construction):OA और OB को मिलाया।
उपपत्ति (Proof): \triangle OCA और \triangle OCB में
OA=OB (एक ही वृत्त की त्रिज्याएँ)
OC=OC (उभयनिष्ठ भुजा)
AC=BC (दिया है)
SSS सर्वांगसमता गुणधर्म से
\triangle OCA \approx \triangle OCB \\ \angle OCA=\angle OCB (CPCT से)
\angle OCA+\angle OCB=180^{\circ} (रैखिक कोण युग्म)
\therefore \angle OCA=180^{\circ} \Rightarrow \angle OCA=90^{\circ}
अतः OC \perp AB
प्रमेय Theorem):10.4.तीन दिए गए असंरेख बिन्दुओं द्वारा होकर जाने वाला एक और एक वृत्त होता है।
Solution:दिया है (Given):तीन असंरेखीय बिन्दु P,Q और R हैं।
सिद्ध करना है (To Prove):P,Q,R से होकर केवल एक अद्वितीय वृत्त खींचा जा सकता है।
रचना (Construction):PQ और QR को मिलाया।PQ और QR के लम्ब समद्विभाजक क्रमशः AL और BM खींचा जो कि परस्पर O पर मिलते हैं।चूँकि P,Q और R असंरेख हैं,इसलिए AL और BM असमान्तर हैं।
माना AL और BM, O पर प्रतिच्छेद करते हैं।OP,OQ और OR को मिलाया।
उपपत्ति (Proof):चूँकि बिन्दु O, लम्ब समद्विभाजकों PQ और QR पर स्थित हैं।
\therefore OP=OQ …..(1)
और OR=OQ ….. (2)
(1) और (2) सेः
OP=OQ=OR=r (माना)
केन्द्र O और त्रिज्या r लेकर एक वृत्त C(O,r) बिन्दुओं P, Q और R से होकर जाता है। इससे सिद्ध होता है P, Q और R से गुजरता हुआ वृत्त है।
प्रश्नावली 10.3
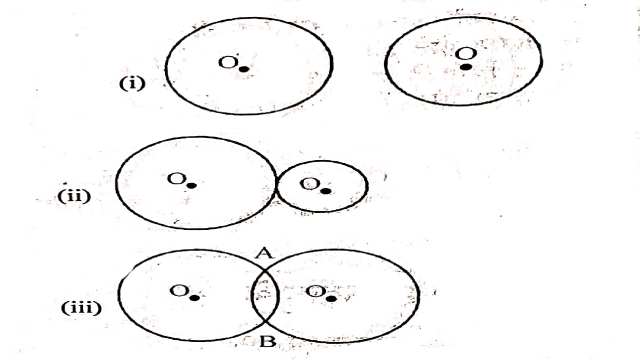
Example:1.वृत्तों के कई जोड़े (युग्म) खींचिए।प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं? उभयनिष्ठ बिन्दुओं की संख्या क्या है?
Solution:
आकृति (i) में, दो वृत्त का कोई उभयनिष्ठ बिन्दु नहीं है।
आकृति (ii) में, दो वृत्त एक दूसरे को स्पर्श करते हैं।
इनका केवल एक उभयनिष्ठ बिन्दु है।
आकृति (iii) में,दो वृत्त एक दूसरे को दो बिन्दुओं पर प्रतिच्छेद करते हैं।
Example:2.मान लीजिए आपको एक वृत्त दिया गया है।एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
Solution:रचना के पद (i)जीवा AB और BC खींची।
(ii)जीवा AB का लम्ब समद्विभाजक ‘l’ खींचा।
(iii)जीवा BC का लम्ब समद्विभाजक ‘m’ खींचा।
(iv)माना l और m का प्रतिच्छेदी बिन्दु O है।
इस प्रकार अभीष्ट केन्द्र O है।
Example:3.यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें,तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
Solution:दिया है (Given):दो वृत्त, जिनके केन्द्र O और O’ हैं, परस्पर बिन्दुओं A तथा B पर प्रतिच्छेद करते हैं।AB उभयनिष्ठ जीवा है।AB का मध्य-बिन्दु M है।
सिद्ध करना है (To Prove):OO’, AB का लम्ब समद्विभाजक है।
उपपत्ति (Proof):हम जानते हैं कि एक जीवा के मध्य बिन्दु और केन्द्र को मिलाने वाला रेखाखण्ड जीवा पर लम्ब होता है।
\therefore \angle OMA=90^{\circ}
और \angle O^{\prime}MA=90^{\circ}
अब \angle OMA+\angle O^{\prime}MA=90^{\circ}+0^{\circ}=180^{\circ}
परन्तु यह रैखिक कोण युग्म हैं इसलिए, OMO’ एक सरल रेखा है।
अतः OO’, AM पर लम्ब समद्विभाजक है।
उपर्युक्त उदाहरणों के द्वारा वृत्त कक्षा 9 (Circle Class 9),जीवा द्वारा एक बिन्दु पर अन्तरित कोण (Angle Subtended by Chord to a Point) को समझ सकते हैं।
5.वृत्त कक्षा 9 की समस्याएँ (Circle Class 9 Problems):
(1.)यदि 16 सेमी लम्बाई की एक जीवा वृत्त के केन्द्र से 6 सेमी की दूरी पर है तो उस वृत्त की त्रिज्या लिखिए।
(2.)दो संकेन्द्रीय वृत्तों जिनका केन्द्र O है, को एक सरल रेखा m, बिन्दुओं A, B, C पर इस प्रकार काटती है कि AD=12 सेमी, BC=8 सेमी है।AB,CD,AC व BD ज्ञात कीजिए।
उत्तर (Answers):(1.) r=10 सेमी (2.)AB=CD=2 सेमी,AC) 10 सेमी, BD=10 सेमी
उपर्युक्त सवालों को हल करने पर वृत्त कक्षा 9 (Circle Class 9),जीवा द्वारा एक बिन्दु पर अन्तरित कोण (Angle Subtended by Chord to a Point) को ठीक से समझ सकते हैं।
Also Read This Article:-Area of Triangles and Parallelograms
6.वृत्त कक्षा 9 (Frequently Asked Questions Related to Circle Class 9),जीवा द्वारा एक बिन्दु पर अन्तरित कोण (Angle Subtended by Chord to a Point) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.वृत्तीय क्षेत्र किसे कहते हैं? (What is Circular Region?):
उत्तर:वृत्त तथा इसका अभ्यंतर मिलकर वृत्तीय क्षेत्र (Circular Region) बनाते हैं।
प्रश्न:2.वृत्त का व्यास किसे कहते हैं? (What is Diameter of a Circle?):
उत्तर:उस जीवा को जो वृत्त के केन्द्र से होकर जाती है, वृत्त का व्यास कहते हैं।त्रिज्या के समान शब्द ‘व्यास’ को भी दो अर्थों में प्रयुक्त किया जाता है अर्थात् एक रेखाखण्ड के रूप में तथा इसकी लम्बाई के रूप में।
प्रश्न:3.लघु वृत्तखण्ड और दीर्घ वृत्तखण्ड किसे कहते हैं? (What are Minor Segment and Major Segment?):
उत्तर:जीवा तथा प्रत्येक चाप के मध्य क्षेत्र को वृत्तीय क्षेत्र का खण्ड कहते हैं।या सरल शब्दों में वृत्तखण्ड कहते हैं।ये दो प्रकार के होते हैं।ये हैं:दीर्घ वृत्तखण्ड (Major Segment) तथा लघु वृत्तखण्ड (Minor Segment)।
उपर्युक्त प्रश्नों के उत्तर द्वारा वृत्त कक्षा 9 (Circle Class 9),जीवा द्वारा एक बिन्दु पर अन्तरित कोण (Angle Subtended by Chord to a Point) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Circle Class 9
वृत्त कक्षा 9 (Circle Class 9)
Circle Class 9
वृत्त कक्षा 9 (Circle Class 9) के इस आर्टिकल में वृत्त,जीवा द्वारा एक बिन्दु पर अन्तरित
कोण तथा तीन बिन्दुओं से जाने वाले वृत्त के बारे में अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.