Cauchy’s Integral Formula
1.कोशी समाकल सूत्र (Cauchy’s Integral Formula),सम्मिश्र विश्लेषण में कोशी समाकल सूत्र (Cauchy Integral Formula in Complex Analysis):
कोशी समाकल सूत्र (Cauchy’s Integral Formula) पर आधारित उदाहरणों के अलावा विश्लेषिक फलनों के अवकलज,मोरेरा प्रमेय (कोशी प्रमेय का विलोम),टेलर एवं लौरां श्रेणी,महत्तम मापांक प्रमेय आदि पर आधारित सवालों को हल करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Complex Integration in ComplexAnalysis
2.कोशी समाकल सूत्र के उदाहरण (Cauchy’s Integral Formula Examples):
Example:1.कोशी समाकल सूत्र से सिद्ध करो कि:
(Using Cauchy’s integral formula,prove that):
Example:1(ii). \int_{|z|=2} \frac{1}{z^4-1} d z=0
Solution: \int_{|z|=2} \frac{1}{z^{4}-1} d z=0 \\ \frac{1}{z^4-1} =\frac{1}{(z+1)(z-1)(z+i)(z-i)} \\ =\frac{A}{z+1}+\frac{B}{z-1}+\frac{C}{z+i}+\frac{D}{z-i} \\ \Rightarrow 1= A(z-1)(z+i)(z-i)+B(z+1)(z+i)(z-i) \\ +C(z+1)(z-1)(z-i)+D(z+1)(z-1)(z+i) \\ \text { put } z=1 \Rightarrow 2(1+i)(1-i) B=1 \Rightarrow B=\frac{1}{4} \\ \text { Put } z=-1 \Rightarrow A(-2)(-1+i)(-1-i)=1 \Rightarrow A=-\frac{1}{4} \\ \text { Put } z=i \Rightarrow D\left(i+1\right)(i-1)(i+1)=1 \Rightarrow D=-\frac{1}{4} i \\ \text { Put } z=-i \Rightarrow C(-i+1)(-i-1)(-2 i)=1 \Rightarrow C=\frac{1}{4} i \\ \int_{|z|=2} \frac{1}{z^4-1} d z=\int_{|z|=2}\left[-\frac{1}{4(z+1)}+\frac{1}{4(z-1)}+\frac{1}{4 i(z+i)}-\frac{1}{4 i(z-i)}\right] dz
वृत्त |z|=2 का केन्द्र (0,0) तथा त्रिज्या 2 है।
जहाँ \int_{|z|=2} \frac{-1}{4(z+1)} d z \text { जहाँ } f(z)=-\frac{1}{4} \\ f(-1)=-\frac{1}{4} \\ \Rightarrow \int_{|z|=2}-\frac{1}{4(z+1)} d z =2 \pi i \cdot f(z)=2 \pi i \left(-\frac{1}{4}\right) \\ =2 \pi i \cdot f(-1) \\ =2 \pi i\left(-\frac{1}{4}\right)=-\frac{1}{2} \pi i \\ \int_{|z|=2} \frac{1}{4(z-1)}=2 \pi i \cdot f(z) \\ =2 \pi i \cdot f(1) \text { जहां } f(2)=\frac{1}{4} \\ =2 \pi i \times \frac{1}{4}=\frac{1}{2} \pi i \\ \int_{|z|=2} \frac{1}{4 i(z+i)} d z =2 \pi i \cdot f(z) \\ =2 \pi i \cdot f(-i) \text { जहां } f(z)=\frac{1}{4 i} \\ =2 \pi i\left(\frac{1}{4 i}\right) =\frac{1}{2} \pi \\ \int_{|z|=2}-\frac{1}{4 i(z-i)} d z=2 \pi i \cdot f(z) \\ =2 \pi i f(i) \text { जहाँ } f(z)=-\frac{1}{4i} \\ =2 \pi i \times -\frac{1}{4i}=-\frac{1}{2} \pi \\ \int_{|z|=2} \frac{1}{z^4-1} d z=-\frac{1}{2} \pi i+\frac{1}{2} \pi i+\frac{1}{2} \pi-\frac{1}{2} \pi \\ \Rightarrow \int_{|z|=2} \frac{1}{z^4-1} d z=0
Example:1(iv). \int_{|z|=5} \frac{\sin 3 z}{z+\frac{\pi}{2}} d z=2 \pi i
Solution: \int_{|z|=5} \frac{\sin 3 z}{z+\frac{\pi}{2}} d z=2 \pi i \\ \text{L.H.S.} \int_{|z|=5} \frac{\sin 3 z}{z+\frac{\pi}{2}} d z
वृत्त का केन्द्र (0,0) तथा त्रिज्या 5 है।
f(z)=\sin 3 z \\ f\left(-\frac{\pi}{2}\right)=\sin 3 \left(-\frac{\pi}{2}\right)=-\sin \frac{3 \pi}{2} \\ =-\sin \left(\pi+\frac{\pi}{2}\right) \\ f\left(-\frac{\pi}{2}\right) =\sin \frac{\pi}{2}=1 \\ \int_{|z|=5} \frac{\sin 3 z}{z+\frac{\pi}{2}} =2 \pi i \cdot f(z) \\ =2 \pi i \cdot f\left(-\frac{\pi}{2}\right) \\ =2 \pi i(1) \\ \Rightarrow \int_{|z|=5} \frac{\sin 3 z}{z+\frac{\pi}{2}} =2 \pi i
Example:1(v). \int_{|z|=5} \frac{e^{-i z}}{z^3} d z=-\pi i
Solution: \int_{|z|=5} \frac{e^{-i z}}{z^3} d z=-\pi i \\ f(z)=e^{-i z} \Rightarrow f^{\prime}(z)=i e^{-i z} \\ f^{\prime \prime}(z)=-e^{-i z} \\ f^{\prime \prime}(0)=-e^{-i(0)}=-e^0=-1 \\ \int_{|z|=5} \frac{e^{-i z}}{z^3} d z =\frac{2 \pi i }{2 !} \cdot f^{\prime \prime}(z)\\ =\frac{2 \pi i }{2} \cdot f^{\prime \prime}(0) \\ = \pi i(-1) \\ \Rightarrow \int_{|z|=5} \frac{e^{-i z}}{z^3} d z=-\pi i
Example:2.मान ज्ञात करो (Evaluate):
Example:2(ii). \frac{1}{2 \pi i} \int_c \frac{e^{z-t}}{\left(z^2+1\right)} d z
जहाँ |z|=3 वृत्त है तथा t>0 (where C is circle |z|=3 and t>0)
Solution: \frac{1}{2 \pi i} \int_c \frac{e^{z-t}}{\left(z^2+1\right)} d z \\ \frac{1}{2 \pi i} \int_c \frac{e^{z t}}{\left(z^2+1\right)} d z=\frac{1}{2 \pi i} \int_c\left[\frac{1}{2 i(z-i)}-\frac{1}{2 i(z+i)]}\right] e^{zt} dz \\ =-\frac{1}{4 \pi}\left[\int_c \frac{1}{z-i} e^{zt} \cdot d z-\int_c \frac{1}{2+i} e^{zt} d z\right] \\ f(z)=e^{z t} \Rightarrow f(i)=e^{i t} \\ f(-i)=e^{-i t} \\ =-\frac{1}{4 \pi}[2 \pi i \cdot f(z)-2 \pi i \cdot f(z)] \\ =-\frac{1}{4 \pi}[2 \pi i \cdot f(i)-2 \pi i \cdot f(-i)] \\ =\frac{-1}{4 \pi}\left[2 \pi i e^{i t}-2 \pi i e^{-i t}\right] \\ =\frac{-2 \pi i}{4 \pi}\left[e^{i t}-e^{-i t}\right] \\ =-i \left[\frac{e^{i t}-e^{-i t}}{2}\right] \\ =\frac{e^{i t}-e^{-i t}}{2 i} \\ =\sin t \\ \Rightarrow \frac{1}{2 \pi i} \int_{c} \frac{e^{z t}}{\left(z^2+1\right)} d z=\sin t
Example:2(iv). \int_c \frac{e^z d z}{(z-1)(z-2)} dz
जहाँ (where) c:|z|=3
Solution: \int_c \frac{e^z d z}{(z-1)(z-2)}
वृत्त का केन्द्र (0,0) तथा त्रिज्या 3 है अतः बिन्दु z=1,2 वृत्त के अन्दर स्थित हैं।अतः f(z) विश्लेषिक है।
\int_c \frac{e^z d z}{(z-1)(z-2)}=\int_c\left[\frac{1}{z-2}-\frac{1}{z-1}\right] e^z d z \\ =\int_c \frac{1}{z-2} e^z d z-\int_c \frac{e^z}{z-1} d z \\ f(z)=e^z \Rightarrow f(z)=e^2 \\ \Rightarrow f(1)=e^1 \\ \int_{c} \frac{e^z d z}{z-2}=2 \pi i \cdot f(z) \\ =2 \pi i \cdot f(2)=2 \pi i e^2 \\ \int_c \frac{e^{z} d z}{z-1}=2 \pi i \cdot f(1)=2 \pi i e \\ \int_c \frac{e^{z} d z}{(z-1)(z-2)}=2 \pi i e^2-2 \pi i e \\ \int_c \frac{e^z d z}{(z-1)(z-2)}=2 \pi i e(e-1)
Example:3.यदि C एक वामावर्त दिशा में खींचा गया संवृत कंटूर है तथा z_{0}, C के अन्दर हो तो प्रदर्शित करो कि
(If C is a closed contour described in the positive sense and is inside C, show that):
\int_c \frac{z^3+2 z}{\left(z-z_0\right)^3} d z=6 \pi i z_0
Solution: \int_c \frac{z^3+2 z}{\left(z-z_0\right)^3} d z=6 \pi i z_0\\ f(z)=z^3+2 z \Rightarrow f^{\prime \prime}(z)=6 z \\ \Rightarrow f^{\prime}\left(z_0\right)=6 z_0 \\ \int_c \frac{z^3+2 z}{\left(z-z_0\right)^3} =\frac{2 \pi i}{2 !} f^{\prime \prime}(z) \\ =\frac{2 \pi i}{2} \times 6 z_0 \\ \Rightarrow \int_c \frac{z^3+2 z}{\left(z-z_0\right)^3} =6 \pi i z_0
Example:4(a).यदि C एक संवृत कंटूर है जिसके अन्दर मूलबिन्दु है तो सिद्ध कीजिए कि:
(If C be a closed contour containing the origin inside it,prove that):
\frac{\alpha^n}{n !}=\frac{1}{2 \pi i} \int_c \frac{e^{\alpha z}}{z^{n+1}} d z
Solution: \frac{\alpha^n}{n !}=\frac{1}{2 \pi i} \int_c \frac{e^{\alpha z}}{z^{n+1}} dz \\ \frac{1}{2 \pi i} \int_c \frac{e^{\alpha z}}{z^{n+1}} d z=\frac{f^n(z)}{n !} \\ f(z)=e^{\alpha z} \Rightarrow f^{\prime}(z)=\alpha e^{\alpha z} \\ f^{\prime \prime}(z)=\alpha^2 e^{\alpha z}, f^{\prime \prime \prime}(z)=\alpha^3 e^{\alpha z} \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots\\ f^{n-1}(z)=\alpha^{n-1} e^{\alpha z} \\ f^n(z)=\alpha^n e^{\alpha z} \\ f^n(0)=\alpha^n e^{\alpha(0)}=\alpha^n \\ \therefore \frac{1}{2 \pi i} \cdot \int_{c} \frac{e^{\alpha z}}{z^{n+1}} d z=\frac{\alpha^n}{n!}
Example:4(b).मान ज्ञात कीजिए (Evaluate):
\int_c \frac{e^{2 z}}{(z+1)^n} d z
जहाँ C वृत्त |z|=2 है तथा n एक धनात्मक पूर्णांक है (where C is the circle and n is a positive integer).
Solution: \int_c \frac{e^{2 z}}{(z+1)^n} d z=\frac{f^{n-1}(z)}{(n-1) !} \cdot 2 \pi i
वृत्त C का केन्द्र (0,0) तथा त्रिज्या 2 है अतः बिन्दु (-1) वृत्त के अन्दर स्थित है।फलतः f(z) विश्लेषिक है।
Example:5.मान ज्ञात करो (Evaluate):
\frac{1}{2 \pi i} \int_{c} \frac{\cos \pi z}{\left(z^2-1\right)} d z
जहाँ C एक वर्ग है जिसके शीर्ष हैं (where C is a square with the vertices at):
Example:5(i). 2 \pm i,-2 \pm i
Solution: \frac{1}{2 \pi i} \int_C \frac{\cos \pi z}{z^2-1} d z \\ =\frac{1}{2 \pi i} \int_c\left\{\frac{1}{2(z-1)}-\frac{1}{2(z+1)} \right] \cos \pi z dz \\ =\frac{1}{4 \pi i} \int_{c} \frac{1}{(z-1)} \cos \pi z d z-\frac{1}{4 \pi i} \int_{c} \frac{1}{z+1} \cos \pi z d z
C एक वर्ग है अतः इसके 2 \pm i,-2 \pm i आठों शीर्ष f(z) के बाहर है अतः उक्त बिन्दुओं पर विश्लेषिक नहीं है।फलतः कोशी समाकल सूत्र से:
\frac{1}{2 \pi i} \int_c \frac{\cos \pi z}{z^{2}-1} d z=\frac{1}{4 \pi i} \int \frac{\cos \pi z}{z-1} dz - \frac{1}{4 \pi i} \int_c \frac{\cos \pi}{z+1} dz=0 \\ \Rightarrow \frac{1}{2 \pi i} \int_c \frac{\cos \pi z}{z^{2}-1} d z
Example:5(ii).-i,2-i,2+i,i
Solution:वर्ग के चारों शीर्ष में सिर्फ -i,f(z) के प्रथम भाग के अन्दर है अतः इस पर विश्लेषिक है।
\frac{1}{4 \pi i} \int_c \frac{\cos \pi z}{z-1} d z=\frac{1}{4 \pi i} 2 \pi i \cdot f(z) \\ =\frac{1}{4 \pi i} 2 \pi i \cdot f(1) \text { जहाँ } f(z)=\cos \pi z \\ =\frac{1}{4 \pi i} 2 \pi i \cos (\pi) \\ =\frac{1}{2}(-1)=-\frac{1}{2} \\ \frac{1}{4 \pi i} \int_c \frac{\cos \pi z}{z+1} d z=0 (कोशी समाकल प्रमेय से)
\therefore \frac{1}{2 \pi i} \int_c \frac{\cos \pi z}{z^2-1} d z=-\frac{1}{2}
Example:13.यदि |f(z)| का \left|z-z_0\right|=r<R पर अधिकतम मान M(r) हो तथा a_n=\frac{f^n\left(z_0\right)}{n !} हो तो प्रदर्शित करिए कि |a_n| \leq \frac{M(r)}{r^n} तथा इससे ल्यूवेल प्रमेय का निगमन कीजिए।
(If |f(z)| has a maximum value M(r) on \left|z-z_0\right|=r<R and if a_n=\frac{f^n\left(z_0\right)}{n !} then show that |a_n| \leq \frac{M(r)}{r^n} and from it deduce Liouville’s theorem.)
Solution:चूँकि f(z),z के सभी परिमित मानों के लिए विश्लेषिक है,अतः f(z) का टेलर प्रमेय की सहायता से प्रसार करने पर:
f(z)=\overset{\infty}{\underset{n=0}{\sum}} a_n\left(z-z_0\right)^n \cdots(1) जहाँ a_n=\frac{f^n\left(z_0\right)}{n !}=\frac{1}{2 \pi i} \int_C \frac{f(z)}{\left(z-z_0\right)^{n+1}} dz
C एक वृत \left|z-z_0\right|=r है।
अब \left|a_n\right| \leq \frac{1}{2 \pi} \int_c \frac{f(z)}{\left(z-z_0\right)^{n+1}}|d z| \\ \leq \frac{M}{2 \pi r^{n+1}} \int_0^{2 \pi}|d z|=\frac{M}{2 \pi r^{n+1}} \cdot 2 \pi r \\ \therefore \left|a_n\right| \leq \frac{M}{r^n} \quad [n=1,2,\cdots ] \cdots(2)
यह असमिका r के प्रत्येक मान के लिए सत्य है चाहे वह कितना ही बड़ा क्यों न हो?
अतः (2) में r \rightarrow \infty लेने परः
a_n=0 \forall n>0 फलतः (1) से f(z)=a_{0} जो कि अचर है यही ल्यूवेल प्रमेय है।
Example:15.निम्नलिखित प्रमेय को स्थापित कीजिए एवं नाम बताइए:
यदि फलन f(z), वृत्त C जिसका केन्द्र तथा त्रिज्या r है, के अन्दर प्रत्येक बिन्दु पर विश्लेषिक है तो C के अन्दर स्थित प्रत्येक बिन्दु पर
(Establish the and name the following theorem:
If a function f(z) is analytic at all points within a circle C with centre and radius r, then at each point z within C)
f(z)=\overset{\infty}{\underset{n=0}{\sum}} a_n\left(z-z_0\right)^n, a_n=\frac{f^n\left(z_0\right)}{n !}, \forall n=0,1,2, \ldots
क्या उपर्युक्त प्रमेय,वास्तविक फलनों के लिए भी होती है?
(Does this theorem exists for function of real variables?)
Solution:टेलर प्रमेय इससे पूर्व लेख में स्थापित की जा चुकी है।अतः उसमें स्थापना देखें।टेलर प्रमेय वास्तविक फलनों के लिए भी होती है।
Example:16.सम्मिश्र फलनों के लिए लौरां प्रमेय का कथन कीजिए।क्या यह प्रमेय वास्तविक फलनों के लिए भी होती है?
(Give statement of Laurent theorem for function of complex variables. Does this theorem exists for functions of real variables?)
Solution:लौरां प्रमेय का कथन तथा स्थापन इससे पूर्व लेख में किया जा चुका है।अतः वहाँ देखें। यह प्रमेय वास्तविक फलनों के लिए नहीं होती है।
Example:17.फलन f(z)=\frac{1}{(z+1)(z+3)} को क्षेत्र 0<|z+1|<2 में (z+1) की घातों में व्यक्त कीजिए एवं इस प्रकार से प्राप्त श्रेणी का नाम बताइए।
(Expand the function f(z)=\frac{1}{(z+1)(z+3)} in powers of z+1 valid in the region 0<|z+1|<2 and name the series thus obtained)
Solution: f(z)=\frac{1}{(z+1)(z+3)} \\ =\frac{1}{2(z+1)}-\frac{1}{2(z+3)} \\ =\frac{1}{2(z+1)}-\frac{1}{2} \frac{1}{(2+z+1)} \\ =\frac{1}{2(z+1)}-\frac{1}{2} \frac{1}{\left(1+\frac{z+1}{2}\right)} \\ =\frac{1}{2(z+1)}-\frac{1}{4}\left(1+\frac{z+1}{2}\right)^{-1} \\ =\frac{1}{2(z+1)}-\frac{1}{4}\left[1-\frac{z+1}{2}+ \left(\frac{z+1}{2}\right)^2-\left(\frac{z+1}{2}\right)^3+ \cdots \cdots \right] \\ \Rightarrow f(z) =\frac{1}{2(z+1)}-\frac{1}{4} \overset{\infty}{\underset{n=0}{\sum}} (-1)^n\left(\frac{z+1}{2}\right)^n
यह लौरां श्रेणी है।
Example:18.क्या कोशी समाकल सूत्र की सहायता से समाकल \int_c \frac{d z}{z}, c:|z|=1 वृत्त है, का मान ज्ञात किया जा सकता है?
(Can we evaluate the intevral \int_c \frac{d z}{z},C is the circle |z|=1 by using Cauchy’s integral formula?)
Solution:हाँ,कोशी समाकल सूत्र से मान ज्ञात किया जा सकता है।
f\left(z_0\right) =\frac{1}{2 \pi i} \int_c \frac{f(z)}{z-z_0} d z से:
\int_c \frac{d z}{z} =2 \pi i \cdot f\left(z_0\right) \\ \Rightarrow \int_c \frac{d z}{z} =2 \pi i \cdot f(0) \quad[f(z)=1] \\ \int_c \frac{d z}{z}=2 \pi i
उपर्युक्त उदाहरणों के द्वारा कोशी समाकल सूत्र (Cauchy Integral Formula),सम्मिश्र विश्लेषण में कोशी समाकल सूत्र (Cauchy’s Integral Formula in Complex Analysis) को समझ सकते हैं।
3.कोशी समाकल सूत्र के सवाल (Cauchy’s Integral Formula Questions):
(1.)मान ज्ञात करो (Evaluate):
\int_c \frac{z^2-4}{z\left(z^2+9\right)} जहाँ C वृत्त |z|=1 है (where C is the circle |z|=1)
(2.)मान ज्ञात करो (Evaluate):
\int_c \frac{z-1}{(z+1)^2(z-2)} d z जहाँ C,|z-i|=2 है (where C: |z-i|=2)
(3.)मान ज्ञात करो (Evaluate):
\int_C \frac{z-3}{z^2+2 z+5} d z जहाँ C वृत्त है (where C is circle)
(a)|z|=1 (b)|z+1-i|=2
उत्तर (Answers): (1.)-\frac{8 \pi i}{9}
(2.) -\frac{2 \pi i}{9}
(3)(a) 0 3(b) \pi(-2+i)
उपर्युक्त सवालों को हल करने पर कोशी समाकल सूत्र (Cauchy Integral Formula),सम्मिश्र विश्लेषण में कोशी समाकल सूत्र (Cauchy Integral Formula in Complex Analysis) को ठीक से समझ सकते हैं।
Also Read This Article:-Bilinear Transformation
4.कोशी समाकल सूत्र (Frequently Asked Questions Related to Cauchy’s Integral Formula),सम्मिश्र विश्लेषण में कोशी समाकल सूत्र (Cauchy Integral Formula in Complex Analysis) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.सम्मिश्र विश्लेषण में मोरेरा प्रमेय को स्थापित करो। (Establish Morera Theorem in Complex Analysis):
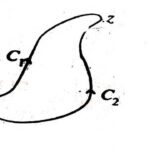
उत्तर:प्रमेय (Theorem):माना एकशः सम्बद्ध प्रदेश G में f(z) विश्लेषिक होगा।
(Let f(z) be a continuous function in a simply connected domain G.if along every simple closed contour.Then f(z) is analytic in G.)
उपपत्ति (Proof):माना कि G में एक स्थिर बिन्दु तथा z एक चर बिन्दु है तथा एवं z को मिलाने वाले दो चापकलनीय वक्र C_{1} एवं C_{2} हैं जो पूर्णतः G में ही हैं।यदि C_{1} एवं C_{2} को मिलाकर बना वक्र C हो तो
\int_c f(z) d z=-\int_{C_1} f(z) d z+\int_{C_2} f(z) d z \\ \therefore 0=-\int_{C_{1}} f(z) d z+\int_{C_2} f(z) d z \\ \therefore \int_{C_{1}} f(z) d z=\int_{C_2} f(z) d z
इसलिए हम कह सकते हैं कि G में तथा z को मिलाने वाले प्रत्येक वक्र के अनुदिश f(z) का समाकलन समान होगा।अतः समाकल का चर \xi लेने पर
F(z)=\int_{z_0}^Z f(\xi) d \xi \ldots(1)
समीकरण (1) में समाकल के लिए प्रयुक्त संकेत उचित है क्योंकि समाकल पथ स्वतन्त्र है तथा यह केवल Z_{0} एवं z पर निर्भर करता है।
माना कि z के समीप G में z+h कोई बिन्दु है तो
F(z+h)=\int_{z_0}^{z+h} f(\xi) d \xi \\ \therefore F(z+h)-F(z)=\int_{z_0}^{z+h} f(\xi) d \xi+\int_z^{z_0} f(\xi) d \xi \\ =\int_{z_0}^{z+h} f(\xi) d \xi
अब चूँकि z तथा z+h को मिलाने वाले पथ से उपर्युक्त समाकल स्वतन्त्र है यदि पथ G में रहे।अतः हम z तथा z+h को मिलाने वाले पथ को एक सरल रेखाखण्ड ले लेते हैं तथा को इतना छोटा लेते हैं ताकि यह सरल रेखाखण्ड पर पूर्णतः G में ही रहे।
अतः \frac{F(z+h)-F(z)}{h}-f(z)=\frac{1}{h} \int_z^{z+h} f(\xi) d \xi-\frac{f(z)}{h} \int_z^{z+h} d \xi \\ =\frac{1}{h} \int_z^{z+h}[f(\xi)-f(z)] d \xi
चूँकि f(\xi) बिन्दु z पर संतत है अतः एक दिए हुए धनात्मक संख्या \varepsilon के लिए एक \delta >0 विद्यमान है कि
|f(\xi)-f(z)|<\varepsilon \cdots(2)
जबकि |\xi-z|< \delta
अब हम h का इस प्रकार चयन करें कि |h|<\delta तो असमिका (2),z तथा z+h को मिलाने वाली रेखाखण्ड के प्रत्येक बिन्दु \xi के लिए सन्तुष्ट होगी अतः
\left|\frac{F(z+h)-F(z)}{h}-f(z)\right| \leq \frac{1}{|h|} \int_z^{z+h}|f(\xi)-f(z)||d \xi| \\ <\frac{\varepsilon}{|h|} \int_z^{z+h}|d \xi|=\frac{\xi}{|h|} \cdot|h| \\ <\varepsilon \cdots(3)
चूँकि \varepsilon स्वेच्छ है अतः (3) से:
\underset{h \rightarrow 0}{\lim} \frac{F(z+h)-f(z)}{h}=f(z) \\ \therefore f^{\prime}(z)=f(z)
अतः F'(z) विद्यमान होगा तथा F'(z)=f(z) फलन F(z),G में विश्लेषिक फलन है।हम जानते हैं कि प्रत्येक विश्लेषिक फलन का अवकलज भी विश्लेषिक फलन होता है।अतः F'(z)=f(z),G में एक विश्लेषिक है।
प्रश्न:2.सम्मिश्र विश्लेषण में कोशी असमिका क्या है? (What is Cauchy’s Inequality?):
उत्तर:प्रमेय (Theorem):माना कि वृत्त C:|z-z_{0}|=r के अन्दर तथा ऊपर f(z) एक विश्लेषिक फलन है।यदि |f(z)| \leq M(r) (या M(R)=\underset{z \in C}{\text{max}} |f(z)|) हो तो
(Let f(z) be analytic inside and on the circle C:|z-z_{0}|=r. If |f(z)| \leq M(r) (or M(R)=\underset{z \in C}{\text{max}} |f(z)| then))
\left|f^n\left(z_0\right)\right| \leq \frac{M(r) n !}{r^n},(n=0,1,2, \ldots)
उपपत्ति (Proof):विश्लेषिक फलन के लिए कोशी समाकल सूत्र से बिन्दु z=z_{0} के लिए
f^n\left(z_0\right)=\frac{n !}{2 \pi i} \int_c \frac{f(z) d z}{\left(z-z_0\right)^{n+1}}
अतः \left|f^n\left(z_0\right)\right| \leq \frac{n !}{| 2 \pi i|} \int_c \frac{|f(z)|}{\left|z-z_0\right|^{n+1}}|d z| \\ \leq \frac{n ! M(r)}{2 \pi} \int \frac{|d z|}{\left|z-z_0\right|^{n+1}} \\ \leq \frac{n ! M(r)}{2 \pi r^{n+1}} \cdot 2 \pi r=\frac{n ! M(r)}{r^n} \\ \therefore\left|f^n\left(z_0\right)\right| \leq \frac{n! M(r)}{r^n}
प्रश्न:3.सम्मिश्र विश्लेषण में प्वासो का समाकल सूत्र स्थापित कीजिए। (Establish Poission Integral Formula in Complex Analysis):
उत्तर:प्रमेय (Theorem):यदि डिस्क C: |z| \leq R के अन्तर्विष्ट करने वाले क्षेत्र में f(z) विश्लेषिक है तो Z=r e^{i \theta}, r<R के लिए
(If f(z) is analytic in a region containing the disc C: |z| \leq R, Then for Z=r e^{i \theta}, r<R, we have)
f\left(r e^{i \theta}\right)=\frac{1}{2 \pi} \int_0^{2 \pi} \frac{R^2-r^2}{R^2-2 r R \cos (\theta-\phi)+r^2} f\left( R e^{i \phi}\right) d \phi
उपपत्ति (Proof):चूँकि फलन f(z) डिस्क C: |z| \leq R के अन्दर तथा ऊपर के प्रत्येक बिन्दु पर विश्लेषिक फलन है इसलिए यदि डिस्क के अन्दर कोई बिन्दु z_{0} हो तो कोशी समाकल सूत्र से
f\left(z_0\right)=\frac{1}{2 \pi i} \int_c \frac{f(z) d z}{z-z_0} \cdots(1)
वृत्त |z|=R के सापेक्ष z_{0} का प्रतिलोम बिन्दु होगा जो कि वृत्त के बाहर स्थित होगा।इसलिए फलन \frac{f(z)}{z-\left(\frac{R^2}{\overline{z_{0}}}\right)} वृत्त C के अन्दर एवं ऊपर विश्लेषिक फलन होगा अतः कोशी प्रमेय से:
0=\frac{1}{2 \pi i} \int_{c} \frac{f(z) dz}{z-\left(\frac{R^2}{\overline{z_{0}}}\right)} \cdots(2)
(1) एवं (2) से:
f\left(z_0\right)=\frac{1}{2 \pi i} \int_c\left[\frac{1}{z-z_0}-\frac{1}{z-\left(\frac{R^2}{\overline{z_{0}}}\right)}\right] f(z) d z \\ =\frac{1}{2 \pi i} \int_{c} \frac{R^2-z_0 \overline{z_0}}{\left(z-z_0\right)\left(R^2-z \bar{z}_0\right)} f(z) d z
अब z_0=r e^{i \theta} और z=R e^{i \phi} लेने पर,
f\left(r e^{i \theta}\right)=\frac{1}{2 \pi i} \int_0^{2 \pi} \frac{\left(R^2-r^2 \right) f(R e^{i \phi}) i R e^{i \phi}}{\left(R e^{i \phi}-r e^{i \theta}\right)\left(R^2-r R e^{i(\phi-\theta)}\right)} d \phi\\ =\frac{1}{2 \pi} \int_0^{2 \pi} \frac{\left(R^2-r^2\right) \cdot f\left(R e^{i \phi}\right)}{R^2-2 R r \cos (\theta-\phi)+r^2} d \phi
टिप्पणी:प्वासो समाकल सूत्र में
f\left(r e^{i \theta}\right)=u(r, \theta)+i v(r, \theta)
और f\left(R e^{i \phi}\right)=u(R, \phi)+i v(R, \phi)
लेने पर तथा वास्तविक एवं काल्पनिक भागों की तुलना करने पर हमें निम्न सम्बन्ध प्राप्त होंगे:
u(r,\theta)=\frac{1}{2 \pi} \int_0^{2 \pi} \frac{\left(R^2-r^2\right) u(R,\phi) d \phi}{R^2-2 R r \cos (\theta-\phi)+r^2} \cdots(3)
और V(r,\theta)=\frac{1}{2 \pi} \int_0^{2 \pi} \frac{\left(R^2-r^2\right) V(R,\phi)}{R^2-2 R r \cos (\theta-\phi)+r^{2}} d \phi \cdots(4)
सूत्र (3) एवं (4) किसी वृत्त के अन्तःस्थ बिन्दु पर फलन के वास्तविक एवं काल्पनिक भाग को वृत्त की परिसीमा एवं काल्पनिक भागों के मानों के रूप में व्यक्त करते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा कोशी समाकल सूत्र (Cauchy’s Integral Formula),सम्मिश्र विश्लेषण में कोशी समाकल सूत्र (Cauchy Integral Formula in Complex Analysis) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Cauchy’s Integral Formula
कोशी समाकल सूत्र
(Cauchy’s Integral Formula)
Cauchy’s Integral Formula
कोशी समाकल सूत्र (Cauchy’s Integral Formula) पर आधारित उदाहरणों के अलावा
विश्लेषिक फलनों के अवकलज,मोरेरा प्रमेय (कोशी प्रमेय का विलोम),टेलर एवं
लौरां श्रेणी,महत्तम मापांक प्रमेय आदि पर आधारित सवालों को हल करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.