JEE MAINS Maths Archive

Quadratic Equation
May 27, 2021
No Comments
1.द्विघात समीकरण (Quadratic Equation),द्विघात समीकरण करना (Quadratic Equations to Solve): द्विघात समीकरण (Quadratic Equation) का हल गुणनखण्ड विधि,पूर्णवर्ग विधि तथा श्रीधराचार्य द्वारा दी गई व्यापक विधि से हल ज्ञात किया जाता है।इस आर्टिकल में विविक्तिकर के अपरिमेय संख्याएं अर्थात् सम्मिश्र संख्या होने की स्थिति में हल ज्ञात करने के बारे में बताया गया है।यहां हम

Inverse Trigonometric Functions
May 15, 2021
No Comments
1.प्रतिलोम त्रिकोणमितीय फलन (Inverse Trigonometric Functions),प्रतिलोम वृत्तीय फलन (Inverse Circular Functions)- प्रतिलोम त्रिकोणमितीय फलन (Inverse Trigonometric Functions):हम जानते हैं कि किसी फलन f का प्रतिलोम फलन ज्ञात करने के लिए फलन f ज्ञात होना आवश्यक है।अतः फलन f ज्ञात करने के लिए f का एकैकी-आच्छादक होना आवश्यक है।त्रिकोणमितीय फलनों के अध्ययन से स्पष्ट है कि
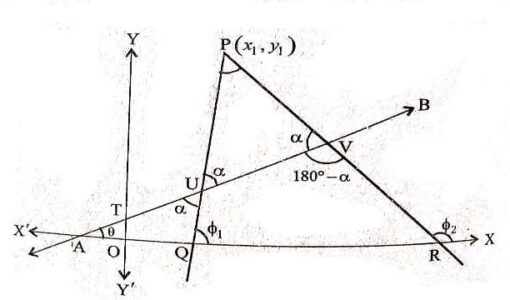
Equation of Line Passing Through Point
May 13, 2021
No Comments
1.दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line)- इस आर्टिकल में दिए हुए बिन्दु से गुजरने

Derivative of Logarithmic Functions
May 3, 2021
No Comments
1.लघुगुणकीय फलनों के अवकलज (Derivative of Logarithmic Functions),लघुगुणकीय अवकलन (Logarithmic Differentiation)- प्रारम्भिक फलन y=f(x) के लघुगुणकीय अवकलन को लघुगुणकीय फलनों के अवकलज (Derivative of Logarithmic Functions) कहा जाता है।यह अवकलन विधि चर-घातांकीय फलनों को प्रभावी ढ़ंग से ज्ञात करने में सहायक है।जब फलन चर-घातांकीय रूप में हो तब ऐसे फलन का अवकलन ज्ञात करने के

Line Passing Through Two Points Equation
April 29, 2021
No Comments
1.दो बिंदुओं से गुजरने वाली रेखा की समीकरण (Line Passing Through Two Points Equation),एक बिन्दु से गुजरने वाली रेखा का समीकरण (Straight Line Passing Through One Point Equation)- दो बिंदुओं से गुजरने वाली रेखा की समीकरण (Line Passing Through Two Points Equation) ज्ञात करने से पूर्व सरल रेखा के व्यापक समीकरण का मानक रूपों में

Tangents and Normals
April 17, 2021
No Comments
1.स्पर्श रेखाएं और अभिलम्ब (Tangents and Normals)- स्पर्श रेखाएं और अभिलम्ब में स्पर्शरेखा(Tangents and Normals) वह सरल रेखा है जो किसी दिए गए बिंदु पर वक्र को स्पर्श करती है। अभिलम्ब ऐसी सरल रेखा है जो स्पर्शरेखा के लंबवत है।यहां हम अवकलन के प्रयोग से किसु दिए गए वक्र के किसी बिन्दु पर स्पर्शरेखा तथा

Equation of Straight Lines
April 15, 2021
No Comments
1.सरल रेखा का समीकरण (Equation of Straight Lines)- सरल रेखा का समीकरण (Equation of Straight Lines) में (1.) सरल रेखा (Straight Line)-सरल रेखा एक चर बिंदु का बिंदुपथ है जिस पर किन्हीं दो बिंदुओं को सीधे मिलाने पर बिंदुपथ के अन्य सभी बिंदु भी इस पर स्थित हो।(2.)सरल रेखा का समीकरण (Equation of Straight Lines)-एक

Differentiation
April 3, 2021
No Comments
1.अवकलन (Differentiation),कक्षा 12 में अवकलन (Differentiation class 12)- अवकलन (Differentiation) की कई विधियों के द्वारा हम समझ चुके हैं।इस आर्टिकल में कुछ उदाहरणों के अवकलन को ओर समझेंगे। इसमें अवकलज का श्रृंखला नियम,दो फलनों के गुणनफल का अवकलज तथा दो फलनों के भागफल का अवकलज के द्वारा अवकलन ज्ञात करना सीखेंगे।आपको यह जानकारी रोचक व

Differentiability
March 20, 2021
No Comments
1.अवकलनीयता (Differentiability),अवकलनीयता तथा सांतत्यता (Differentiability and Continuity)- अवकलनीयता (Differentiability) को हम एक विशेष सीमा प्रक्रिया के प्रयोग से ज्ञात करने की विधि का अध्ययन करेंगे।यदि वक्र का समीकरण y=f(x) है तब फलन f(x) इस वक्र के किसी बिन्दु x=a पर अवकलनीय कहलाता है यदि वक्र के इस बिन्दु पर स्पर्श रेखा खींची जा सके।यदि बिन्दु

Sum of Series by Difference Method
March 18, 2021
No Comments
1.अन्तर विधि से श्रेणी का योगफल (Sum of Series by Difference Method)- अन्तर विधि से श्रेणी का योगफल (Sum of Series by Difference Method) गुणोत्तर श्रेढ़ी के पद युग्मों के अंतर वाली श्रेणी में प्रयोग किया जाता है अर्थात् यदि किसी श्रेणी में क्रमागत युग्मों का अंतर गुणोत्तर श्रेढ़ी में हो ऐसी श्रेणी का योगफल









