Differential Calculus Archive

Total Differential Co-efficient
August 24, 2020
No Comments
1.सम्पूर्ण अवकल गुणांक का परिचय (Introduction to Total Differential Co-efficient)- (1.) f(x,y) का सम्पूर्ण अवकलज ज्ञात करें (x y)find the total derivative of f(x y)- सम्पूर्ण अवकल गुणांक (Total Differential Co-efficient) में दो चर x एवं y फलन माना z=f(x,y) है। अब यदि x एवं y किसी अन्य चर t पर निर्भर करते हों तो

Radius of curvature for polar equation
July 16, 2020
No Comments
1.ध्रुवी समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for polar equation)- ध्रुवी समीकरण के लिए वक्रता त्रिज्या (Radius of curvature for polar equation) ज्ञात करने के लिए वक्रता त्रिज्या का ज्ञान होना आवश्यक है।वक्र के किसी बिन्दु पर खींचे गए वृत्त की त्रिज्या को वक्रता त्रिज्या कहते हैं।इससे पूर्व प्राचलिक वक्रों की वक्रता त्रिज्या

Euler theorem of homogeneous function
July 6, 2020
No Comments
1.समघात पर आयलर प्रमेय (Euler theorem of homogeneous function)- समघात फलन पर आयलर प्रमेय (Euler theorem of homogeneous function) को कुछ सवालों के हल द्वारा समझेंगे।समघात फलन का अर्थ होता है कि दो या दो से अधिक चरों के फलन में प्रत्येक पद के चरों की घातों का योग सदैव समान रहता है।समघात फलन पर

Euler theorem of homogeneous functions
June 19, 2020
No Comments
1.समघात फलनों पर आयलर प्रमेय का परिचय (Introduction to Euler theorem of homogeneous functions)- समघात फलनों पर आयलर प्रमेय (Euler theorem of homogeneous functions) का अध्ययन करने से पहले हमें समघात फलन को जानना आवश्यक है।समघात फलन (Homogeneous functions)-(1.)दो या दो से अधिक चरों का फलन f,एक ऐसा व्यंजक हो कि इसके प्रत्येक पद में
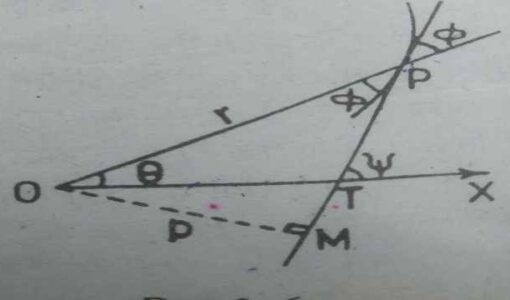
Perpendicular length pole on tangent
May 13, 2020
No Comments
1.स्पर्श रेखा पर ध्रुव से लम्ब की लम्बाई का परिचय (Introduction to Perpendicular length pole on tangent)- स्पर्श रेखा पर ध्रुव से लम्ब की लम्बाई(Perpendicular length pole on tangent) ज्ञात करने के लिए इसमें प्रयुक्त होने वाली शब्दावली ध्रुव,ध्रुवान्तर रेखा,प्रारम्भिक रेखा का ज्ञान होना आवश्यक है।आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों

coordinates of centre of curvature
May 11, 2020
No Comments
1.वक्रता केन्द्र के निर्देशांक का परिचय (Introduction to coordinates of centre of curvature): वक्रता केन्द्र के निर्देशांक(coordinates of centre of curvature) को समझने के लिए वक्रता केन्द्र को समझना आवश्यक है।जब तक हमें किसी थ्योरी की बेसिक बातों की जानकारी नहीं होती है तब तक वह थ्योरी समझ में नहीं आती है।वक्रता केन्द्र ( centre
Radius curvature for parametric curves
May 7, 2020
No Comments
1.प्राचलिक वक्रों की वक्रता त्रिज्या का परिचय (Introduction to Radius curvature for parametric curves)- प्राचलिक वक्रों की वक्रता त्रिज्या (Radius curvature for parametric curves) ज्ञात करने के लिए सर्वप्रथम हमें प्राचल,प्राचलिक समीकरण,प्राचलिक वक्र तथा वक्रता त्रिज्या को समझना होगा।आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को
Homogeneous function question with solution
May 29, 2019
No Comments
सजातीय फ़ंक्शन प्रश्न के समाधान के साथ (Homogeneous Function Question with Solution): समघात फलन (Homogeneous Function): सजातीय फ़ंक्शन प्रश्न के समाधान के साथ (Homogeneous Function Question with Solution):यदि किसी फ़ंक्शन में होने वाला प्रत्येक शब्द उसी डिग्री का है, तो n कहते हैं, तो फ़ंक्शन को nth डिग्री का एक सजातीय फ़ंक्शन कहा जाता है।

convergence of series
May 27, 2019
No Comments
श्रेणी का अभिसरण का परिचय (Introduction to Convergence of Series): श्रेणी का अभिसरण का (Convergence of Series):एक अनुक्रम अभिसारी (Covergent) कहलाता है यदि इसकी सीमा परिमित (finite) हो अर्थात यदि की सीमा परिमित हो तो अनुक्रम , को अभिसृत होता है तथा इसे निम्न प्रकार लिखा जाता है. आपको यह जानकारी रोचक व ज्ञानवर्धक लगे

Partial Differentiation
March 30, 2019
2 Comments
आंशिक अवकलन का परिचय (Introduction to Partial Differentiation)(Differential Calculus): आंशिक अवकलन (Differentiation):जब दो स्वतंत्र चरों मेँ से जब एक के सापेक्ष अवकलन किया जाता है तो दूसरे चर को अचर मान लिया जाता है इसी प्रकार जब दूसरे चर के सापेक्ष अवकलन किया जाता है तो पहले चर को अचर मान लिया जाता है और









