9th Mathematics Archive
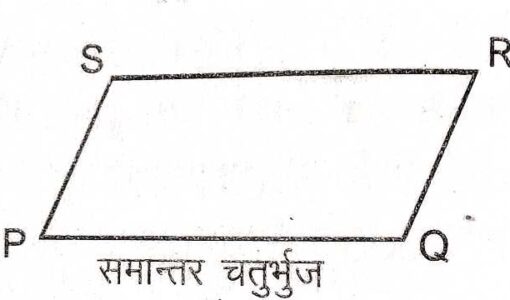
Properties of Parallelogram
March 28, 2021
No Comments
1.समान्तर चतुर्भुज के गुणधर्म (Properties of Parallelogram)- समान्तर चतुर्भुज के गुणधर्मो (Properties of Parallelogram) का अध्ययन करने के लिए हमें कुछ परिभाषाओं का अध्ययन करना होगा।(1.)चतुर्भुज (Quadrilateral):चार भुजाओं से घिरी हुई आकृति को चतुर्भुज कहते हैं।एक चतुर्भुज में चार भुजाएं,चार कोण एवम् चार शीर्ष होते हैं।जैसा कि चित्र में चतुर्भुज PQRS में PQ,QR,RS तथा SP

Inequalities of triangle class 9
March 14, 2021
No Comments
1.त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9)- त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9) में हम अध्ययन करेंगे कि त्रिभुज की भुजाओं के माप बदलने पर उसके कोणों के माप भी बदल जाते हैं और यदि त्रिभुज के कोणों के माप बदलें तो भुजाओं के माप भी बदल जाते

Lines and Angles for Class 9
February 26, 2021
No Comments
1.कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9), रेखाएं और कोण कक्षा 9 (Lines and Angles Class 9)- कक्षा 9 के लिए रेखाएं और कोण (Lines and Angles for Class 9) में कोण के प्रकार,एक बिन्दु पर बननेवाले कोण,दो रेखाओं के साथ तिर्यक रेखा द्वारा बनाए गए कोणों का अध्ययन

Congruence of Triangles
February 14, 2021
No Comments
1.त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules)- त्रिभुजों की सर्वांगसमता (Congruence of Triangles),सर्वांगसम त्रिभुजों के नियम (Congruent Triangles Rules) में एक त्रिभुज के तीनों कोण से दूसरे त्रिभुज के तीनों कोण बराबर होने पर दोनों त्रिभुजों का सर्वांगसम होना आवश्यक नहीं है।(1.)भुजा-भुजा-भुजा सर्वांगसमता नियम (SSS Property Rule)-यदि एक त्रिभुज की

Properties of Triangles class 9
January 29, 2021
No Comments
1.त्रिभुजों के गुणधर्म कक्षा 9 (Properties of Triangles class 9)- त्रिभुजों के गुणधर्म कक्षा 9 (Properties of Triangles class 9) में त्रिभुज की सर्वांगसमता का प्रयोग करके समद्विबाहु त्रिभुज सम्बन्धित प्रमेयों एवं त्रिभुज की सर्वांगसमता की शेष प्रमेयों को सिद्ध करने के लिए करेंगे।(1.)समद्विबाहु त्रिभुज (Isoscecles Triangle)-एक त्रिभुज समद्विबाहु त्रिभुज कहलाता है यदि इसकी दो

Surface Area of Cube and Cuboid
January 17, 2021
No Comments
1.घन और घनाभ का पृष्ठीय क्षेत्रफल (Surface Area of Cube and Cuboid)- घन और घनाभ का पृष्ठीय क्षेत्रफल (Surface Area of Cube and Cuboid) में ठोस आकृतियां जैसे ईंट,माचिस,चाक का डिब्बा,सन्दूक,कमरा,पुस्तक इत्यादि का ज्ञात करना सीखेंगे। इन सभी वस्तुओं का आकार और आयतन निश्चित होता है।ये सभी आकृतियां त्रिविमीय ठोस आकृतियां हैं अर्थात् इनकी लम्बाई,चौड़ाई

Trigonometric Ratios of Acute Angle
December 12, 2020
No Comments
1.न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle)- न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) समकोण त्रिभुज के लिए ज्ञात करना सीखेंगे। समकोण त्रिभुज जिसका एक कोण समकोण है। समकोण के सम्मुख भुजा को कर्ण कहते हैं।किसी समकोण त्रिभुज के अन्य दो कोणों के सन्दर्भ में किसी कोण को बनाने

Method of elimination by equating coefficients
December 2, 2020
No Comments
1.गुणांकों को समान बनाकर विलोपन विधि (Method of elimination by equating coefficients)- गुणांकों को समान बनाकर विलोपन विधि (Method of elimination by equating coefficients) से युगपत समीकरणों का बीजीय हल ज्ञात किया जाता है।युगपत समीकरण दो चरों वाले रैखिक समीकरणों के जोड़े का एक निकाय है। दोनों चरों के वे मान जो दोनों समीकरणों को

Algebraic identities
November 20, 2020
No Comments
1.बीजीय सर्वसमिकाओं का परिचय (Introduction to Algebraic identities),कक्षा 9 के लिए बीजीय सर्वसमिकाएं (Algebraic Identities for class 9)- बीजीय सर्वसमिकाएं (Algebraic identities),कक्षा 9 के लिए बीजीय सर्वसमिकाएं (Algebraic Identities for class 9) ऐसी बीजीय समीकरण होती है जो चर के वास्तविक मानों के लिए सत्य होती है।इस आर्टिकल में उन सर्वसमिकाओं का अध्ययन करेंगे जो

Cross multiplication method
November 6, 2020
No Comments
1.वज्र गुणन विधि (Cross multiplication method,cross multiplication method class 10)- वज्र गुणन विधि (Cross multiplication method,cross multiplication method class 10) से युगपत समीकरणों को हल करने के लिए इसका व्यापक विधि के रूप में प्रयोग किया जाता है।युगपत समीकरणों को हल करने की विधि नीचे स्पष्ट की गई है-(1.)वज्र गुणन विधि सूत्र (Cross multiplication method









