11th Mathematics Archive

Equation of Straight Line
June 10, 2021
No Comments
1.सरल रेखा का समीकरण (Equation of Straight Line),दो बिन्दुओं से गुजरने वाली रेखा का समीकरण (Equation of Straight Line Passing Through Two Points): सरल रेखा का समीकरण (Equation of Straight Line):एक सरल रेखा का झुकाव रूप समीकरण y = mx + c है, जहाँ m ढाल है और y = c वह मान है जहाँ

Quadratic Equation
May 27, 2021
No Comments
1.द्विघात समीकरण (Quadratic Equation),द्विघात समीकरण करना (Quadratic Equations to Solve): द्विघात समीकरण (Quadratic Equation) का हल गुणनखण्ड विधि,पूर्णवर्ग विधि तथा श्रीधराचार्य द्वारा दी गई व्यापक विधि से हल ज्ञात किया जाता है।इस आर्टिकल में विविक्तिकर के अपरिमेय संख्याएं अर्थात् सम्मिश्र संख्या होने की स्थिति में हल ज्ञात करने के बारे में बताया गया है।यहां हम
Equation of Line Passing Through Point
May 13, 2021
No Comments
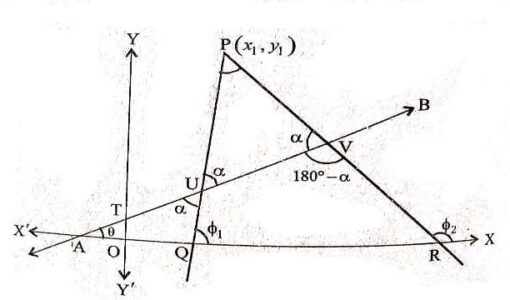
1.दिए हुए बिन्दु से गुजरने वाली रेखा की समीकरण (Equation of Line Passing Through Point),दिए हुए बिन्दु से गुजरने वाली एवं दी हुई सरल रेखा से निर्धारित कोण बनाने वाली रेखा का समीकरण (Equation of line passing through given point and making certain angle with given line)- इस आर्टिकल में दिए हुए बिन्दु से गुजरने

Line Passing Through Two Points Equation
April 29, 2021
No Comments
1.दो बिंदुओं से गुजरने वाली रेखा की समीकरण (Line Passing Through Two Points Equation),एक बिन्दु से गुजरने वाली रेखा का समीकरण (Straight Line Passing Through One Point Equation)- दो बिंदुओं से गुजरने वाली रेखा की समीकरण (Line Passing Through Two Points Equation) ज्ञात करने से पूर्व सरल रेखा के व्यापक समीकरण का मानक रूपों में

Equation of Straight Lines
April 15, 2021
No Comments
1.सरल रेखा का समीकरण (Equation of Straight Lines)- सरल रेखा का समीकरण (Equation of Straight Lines) में (1.) सरल रेखा (Straight Line)-सरल रेखा एक चर बिंदु का बिंदुपथ है जिस पर किन्हीं दो बिंदुओं को सीधे मिलाने पर बिंदुपथ के अन्य सभी बिंदु भी इस पर स्थित हो।(2.)सरल रेखा का समीकरण (Equation of Straight Lines)-एक

Sum of First n Natural Numbers
April 1, 2021
No Comments
1.प्रथम n प्राकृत संख्याओं का योगफल (Sum of First n Natural Numbers)- प्रथम n प्राकृत संख्याओं का योगफल (Sum of First n Natural Numbers),प्रथम n प्राकृत संख्याओं के वर्गों का योगफल,प्रथम n प्राकृत संख्याओं के घनों का योगफल के सूत्रों की स्थापना तथा कुछ उदाहरणों के द्वारा योगफल ज्ञात करेंगे।(1.)प्रथम n प्राकृत संख्याओं का योगफल

Sum of Series by Difference Method
March 18, 2021
No Comments
1.अन्तर विधि से श्रेणी का योगफल (Sum of Series by Difference Method)- अन्तर विधि से श्रेणी का योगफल (Sum of Series by Difference Method) गुणोत्तर श्रेढ़ी के पद युग्मों के अंतर वाली श्रेणी में प्रयोग किया जाता है अर्थात् यदि किसी श्रेणी में क्रमागत युग्मों का अंतर गुणोत्तर श्रेढ़ी में हो ऐसी श्रेणी का योगफल

Sum of Terms of Geometric Progression
March 4, 2021
No Comments
1.गुणोत्तर श्रेढ़ी के पदों का योगफल (Sum of Terms of Geometric Progression),अनन्त गुणोत्तर श्रेढ़ी का योगफल के लिए सूत्र (Formula for Sum of Infinite Geometric Series)- गुणोत्तर श्रेढ़ी के पदों का योगफल (Sum of Terms of Geometric Progression) से तात्पर्य है कि गुणोत्तर श्रेढ़ी के प्रथम n पदों का योगफल ज्ञात करना।माना कि किसी गुणोत्तर

Limit of a Function
February 18, 2021
No Comments
1.फलन की सीमा (Limit of a Function),फंक्शन की सीमा की परिभाषा (Limit of a Function Definition)- फलन की सीमा (Limit of a Function) ज्ञात करने की कई विधियां हैं। इनमें मुख्य रूप से प्रतिस्थापन विधि (Substitution Method),व्यंजक सरलीकरण विधि (Expressions Simplification Method),परिमेयकरण या द्विपरिमेयकरण विधि (Rationalization or Birationalization Method),प्रसार विधि (Expressions Method), सरलीकरण विधि (Simplification

Existence of Limit
February 4, 2021
No Comments
1.सीमा का अस्तित्व (Existence of Limit)- सीमा का अस्तित्व (Existence of Limit)-एक नियमित बहुभुज जो एक वृत्त के अन्तर्गत है,के क्षेत्रफल पर विचार करने पर हम देखते हैं कि(i) बहुभुज की भुजाओं की संख्या कितनी भी हो उसका क्षेत्रफल वृत्त के क्षेत्रफल से अधिक नहीं होता है।(ii) जैसे-जैसे बहुभुज की भुजाओं की संख्या बढ़ाते जाते









