Binomial Theorem Class 11
1.द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11),कक्षा 11 में द्विपद प्रमेय (Binomial Theorem in Class 11):
द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11) द्वारा अधिक घात वाली संख्याओं की गणना,क्रमिक गुणनफल की अधिक जटिल प्रक्रिया को दूर किया जा सकता है।इस आर्टिकल में केवल धन पूर्णांकों के लिए द्विपद प्रमेय का अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Combinations Class 11
2.द्विपद प्रमेय कक्षा 11 के साधित उदाहरण (Binomial Theorem Class 11 Solved Examples):
प्रश्न 1 से 5 तक प्रत्येक व्यंजक का प्रसार कीजिए:
Example:1. (1-2 x)^5
Solution: (1-2 x)^5 \\ (1-x)^n={}^n C_0-{}^n C_1 x+{}^n C_2 x^2-{}^n C_3 x^3+\ldots \ldots+(-1)^n {}^n C_n x^n सूत्र से:
={}^5 C_0-{}^5 C_1(2 x)+{}^5 C_2 \cdot(2 x)^2-{}^5 C_3 (2 x)^3+{}^5 C_4 (2 x)^4-{}^5 C_5 (2 x)^5 \\ =1-10 x+40 x^2-80 x^3+80 x^4-32 x^5
Example:2. \left(\frac{2}{x}-\frac{x}{2}\right)^5
Solution: \left(\frac{2}{x}-\frac{x}{2}\right)^5 \\ (x-y)^n={}^n C_0 x^x-{}^n C_1 x^{n-1} y+{}^n C_2 x^{n-2} y^2+\ldots \ldots + (-1)^n {}^n C_n y^n सूत्र से:
={}^5 C_0 \left(\frac{2}{x}\right)^5-{}^5 C_1 \left(\frac{2}{x}\right)^4\left(\frac{x}{2}\right)+{}^5 C_2 \left(\frac{2}{x}\right)^3\left(\frac{x}{2}\right)^2 -{}^5 C_3 \left(\frac{2}{x}\right)^2\left(\frac{x}{2}\right)^3+ {}^5 C_4 \left(\frac{2}{x}\right)\left(\frac{x}{2}\right)^4 -{}^5 C_5 \left(\frac{x}{2}\right)^5 \\ =\frac{32}{x^5}-\frac{80}{x^4} \cdot \frac{x}{2}+\frac{80}{x^3} \times \frac{x^2}{4}-\frac{40}{x^2} \times \frac{x^3}{8} +\frac{10}{x} \times \frac{x^4}{16}-\frac{x^5}{32} \\ =\frac{32}{x^5}-\frac{40}{x^3}+\frac{20 x}{x}-5 x+\frac{5}{8} x^3-\frac{x^5}{32}
Example:3. (2 x-3)^6
Solution: (2 x-3)^6 \\ (x-y)^n={}^n C_0 x^n-{}^n C_1 x^{n-1} y+{}^n C_2 x^{n-2} y^2+\ldots \ldots + (-1)^n {}^n C_n y^n सूत्र से:
={}^6 C_0 (2 x)^6-{}^6 C_1 (2 x)^5(3)+{}^6 C_2 (2 x)^4(3)^2-{}^6 C_3 (2 x)^3(3)^3+{}^6 C_4 (2 x)^2(3)^4-{}^6 C_5 (2x) (3)^5+{}^6 C_6 (3)^6 \\ =64 x^6-6 \times 32 x^5 \times 3+15 \times 16 x^4 \times 9 -20 \times 8 x^3 \times 27+15 \times 4 x^2 \times 81-6 \\ \times 2 x \times 243+729 \\ =64 x^6-576 x^5+2160 x^4-4320 x^3 +4860 x^2-2916 x+729
Example:4. \left(\frac{x}{3}+\frac{1}{x}\right)^5
Solution: \left(\frac{x}{3}+\frac{1}{x}\right)^5 \\ (a+b)^n={}^n C_0 a^n-{}^n C_1 a^{n-1} b+{}^n C_2 a^{n-2} b^2+\ldots \ldots +{}^n C_{n-1}a b^{n-1}+{}^n C_n b^n सूत्र से:
={}^5 C_0\left(\frac{x}{3}\right)^5+{}^5 C_1 \left(\frac{x}{3}\right)^4\left(\frac{1}{x}\right)+{}^5 C_2 \left(\frac{x}{3}\right)^3\left(\frac{1}{x}\right)^2 +{}^5 C_3 \left(\frac{x}{3}\right)^2\left(\frac{1}{x}\right)^3 +{}^5 C_4 \left(\frac{x}{3}\right)\left(\frac{2}{x}\right)^4+{}^5 C_5 \left(\frac{1}{x}\right)^5 \\ =\frac{x^5}{243}+5 \times \frac{x^4}{81} \times \frac{1}{x}+10 \times \frac{x^3}{27} \times \frac{1}{x^2} +10 \times \frac{x^2}{9} \times \frac{1}{x^3}+5 \times \frac{x}{3} \times \frac{1}{x^4}+\frac{1}{x^5} \\=\frac{x^5}{243}+\frac{5}{81} x^3+\frac{10}{27} x+\frac{10}{9 x}+\frac{5}{3} \cdot \frac{1}{x^3}+\frac{1}{x^5}
Example:5 \left(x+\frac{1}{x}\right)^6
Solution: \left(x+\frac{1}{x}\right)^6 \\ (a+b)^n={}^n C_0 a^n-{}^n C_1 a^{n-1} b+{}^n C_2 a^{n-2} b^2+\ldots \ldots +{}^n C_{n-1}a b^{n-1}+{}^n C_n b^n[/katex] सूत्र से:
={}^6 C_0 x^6+ {}^6 C_1 (x)^5\left(\frac{1}{x}\right)+{}^6 C_2 x^4\left(\frac{1}{x^2}\right)+{}^6 C_3\left(x^3\right)\left(\frac{1}{x^3}\right)+{}^6 C_4 \left(x^2\right)\left(\frac{1}{x^4}\right)+{}^6 C_5 (x)\left(\frac{1}{x^5}\right)+{}^6 C_6 \left(\frac{1}{x^6}\right) \\ =x^6+6 x^4+15 x^2+20+\frac{15}{x^2}+\frac{6}{x^4}+\frac{1}{x^6}
द्विपद प्रमेय का प्रयोग करके निम्नलिखित का मान ज्ञात कीजिए:
Example:6. (96)^3
Solution: (96)^3 \\ =(100-4)^3 ={}^3 C_0(100)^3-{}^3 C_1(100)^2(4)+{}^3 C_2(100)(4)^2-{}^3 C_3(4)^3 \\=1000000-120000+4800-64 \\=884736
Example:7. (102)^5
Solution: (102)^5 \\ =(100+2)^5 \\ ={}^5 C_0(100)^5+{}^5 C_1(100)^4(2)+{}^5 C_2(100)^3 (2)^2+{}^5 C_3(100)^2(2)^3+{}^5 C_4(100)(2)^4 +{}^5 C_5\left(2^5\right) \\ =10000000000+1000000000+ 4000000+ 800000+8000+32 \\ =11040808032
Example:8. (101)^4
Solution: (101)^4 \\ =(100+1)^4 \\ ={}^4 C_0(100)^4+{}^4 C_1(100)^3(1)+{}^4 C_2(100)^2(1)^2+{}^4 C_3(100)(1)^3+{}^4 C_4(1)^4 \\ =100000000+4000000+60000+400+1 \\ =104060401
Example:9. (99)^5
Solution: (99)^5 \\ =(100-1)^5 \\ ={}^5 C_0(100)^5-{}^5 C_1(100)^4(1)+{}^5 C_2(100)^3(1)^2 -{}^5 C_3(100)^2(1)^3+{}^5 C_4(100)(1)^4-{}^5 C_5(1)^5 \\ =10000000000-500000000+10000000 -100000+500-1 \\ =9509900499
Example:10.द्विपद प्रमेय का प्रयोग करते हुए बताइए कौनसी संख्या बड़ी है (1.1)^{10000} या 1000.
Solution:1.1 को दो पदों में व्यक्त करके द्विपद प्रमेय के पहले कुछ पदों को लिखकर हम पाते हैं
(1.1)^{10000}=(1+0.1)^{10000} \\ =10000 C_0 + 10000 C_{1} (0.1)+अन्य धनात्मक पद
=1+1000 (0.1)+अन्य धनात्मक पद
=1+1000+अन्य धनात्मक पद
=1001+अन्य धनात्मक पद
1000
अतः (1.1)^{10000}>1000
Example:11. (a+b)^4-(a-b)^4 का विस्तार कीजिए।इसका प्रयोग करके (\sqrt{3}+ \sqrt{2})^{4} -(\sqrt{3}-\sqrt{2})^{4} का मान ज्ञात कीजिए।
Solution: (a+b)^4-(a-b)^4 \\ (a+b)^4={}^4 C_0 a^4+{}^4 C_1 a^3 b+{}^4 C_2 a^2 b^2+{}^4 C_3 a b^3+{}^4 C_4 b^4 \\ \Rightarrow (a+b)^4= a^4+4 a^3 b+6 a^2 b^2+4 a b^3+b^4 \\ (a-b)^4= {}^4 C_0 a^4-{}^4 C_1 a^3 b+{}^4 C_2 a^2 b^2-{}^4 C_3 a b^3 +{}^4 C_4 b^4 \\ \Rightarrow (a-b)^4=a^4-4 a^3 b+6 a^2 b^2-4 a b^3+b^4
अतः (a+b)^4-(a-b)^4=a^4+4 a^3 b+6 a^2 b^2+4 a^3+b^4-\left(a^4-4 a^3 b+6 a^2 b^2-4 a b^3+b^4\right) \\ =a^4+4 a^3 b+6 a^2 b^2+4 a b^3+b^4-a^4-6 a^2 b^2+4 a b^3-b^4 \\ =8 a^3 b+8 a b^3 \\ \Rightarrow (a+b)^4-(a-b)^4=8 a b\left(a^2+b^2\right)
उपर्युक्त में a=\sqrt{3}, b=\sqrt{2} रखने परः
(\sqrt{3}+\sqrt{2})^4-(\sqrt{3}-\sqrt{2})^4 =8 \times \sqrt{3} \times \sqrt{2}\left[(\sqrt{3})^2+(\sqrt{2})^2\right] \\=8 \sqrt{6}(3+2) \\ =40 \sqrt{6} \\ \Rightarrow(\sqrt{3}+\sqrt{2})^4-(\sqrt{3}-\sqrt{2})^4=40 \sqrt{6}
Example:12. (x+1)^6+(x-1)^6 का मान ज्ञात कीजिए।इसका प्रयोग करके या अन्यथा (\sqrt{2}+1)^6+(\sqrt{2}-1)^6 का मान ज्ञात कीजिए।
Solution: (x+1)^6={}^6 C_0 x^6+{}^6 C_1 x^5(1)+{}^6 C_2 x^1(1)^2+{}^6 C_3 x^3 (1)^3+{}^6 C_4 x^2 (1)^4 +{}^6 C_5 x^2(1)^5+{}^6 C_6(1)^6 \\ =x^6+6 x^5+15 x^4+20 x^3+15 x^2+6 x+1
इसी प्रकार (x-1)^6=x^6-6 x^5+15 x^4-20 x^3+15 x^2-6 x+1
अतः (x+1)^6+(x-1)^6=x^6+6 x^5+15 x^4+20 x^3+15 x^2+6 x+1+x^6-6 x^5+15 x^4-20 x^3+15 x^2-6 x+1 \\ \Rightarrow (x+1)^6+(x-1)^6=2 x^6+30 x^4+30 x^2+2 \\ \Rightarrow (x+1)^6+(x-1)^6= 2\left(x^6+15 x^4+15 x^2+1\right)
उपर्युक्त x=\sqrt{2} में रखने परः
(\sqrt{2}+1)^6+(\sqrt{2}-1)^6 =2\left[(\sqrt{2})^6+15(\sqrt{2})^4+15(\sqrt{2})^2+1\right] \\ =2(8+60 +30+1) \\ =2 \times 99 \\ \Rightarrow(\sqrt{2}+1)^6+(\sqrt{2}-1)^6 =198
Example:13.दिखाइए कि 9^{n+1}-8 n-9,64 से विभाज्य है जहाँ n एक पूर्णांक है।
Solution:दो संख्याओं a और b के लिए यदि हम संख्याएँ q और r प्राप्त कर सके ताकि a=bq+r तो हम कह सकते हैं कि a को b से भाग देने पर q भजनफल तथा r शेषफल प्राप्त होता है।इसी प्रकार यह दर्शाने के लिए कि 9^{n+1}-8 n-9 ,64 से विभाज्य है।हमें सिद्ध करना है:
9^{n+1}-8 n-9=64k जहाँ k एक प्राकृत संख्या है।
हम जानते हैं: (1+a)^n={}^n C_0+{}^n C_1 a+{}^n C_2 a^2+\ldots \ldots+{}^n C_n a^n
n=n+1,a=8 के लिए हमें प्राप्त होता है:
(1+8)^{n+1}={}^{n+1} C_0+{}^{n+1} C_1 8+{}^{n+1} C_2(8)^2+{}^{n+1} C_3 (8)^3+\ldots+{}^{n+1} C_{n+1} 8^{n+1} \\ \Rightarrow 9^{n+1}= n+1+8(n+1)+64 n+{}^1 C_2+n+{}^1 C_3(512)+\ldots+8^{n+1} \\ \Rightarrow 9^{n+1}=9 n+9+64\left[{}^{n+1} C_2+8 \cdot {}^{n+1} C_3+\cdots+8^{n-1}\right] \\ \Rightarrow 9^{n+1}-9 n-9=64 k जहाँ k={}^{n+1} C_2+8 \cdot {}^{n+1} C_3+\cdots+8^{n-1}
यह दर्शाता है कि 9^{n+1}-8 n-9,64 से विभाज्य है।
Example:14.सिद्ध कीजिए कि \underset{r=0}{\overset{n}{\Sigma}}=3^r \cdot {}^n C_r=4^n
Solution: \underset{r=0}{\overset{n}{\Sigma}}=3^r \cdot {}^n C_r=4^n \\ (a+b)^n={}^n C_0 a^n-{}^n C_1 a^{n-1} b+{}^n C_2 a^{n-2} b^2+\ldots \ldots +{}^n C_{n-1}a b^{n-1}+{}^n C_n b^n
a=3,b=1 रखने परः
\Rightarrow(3+1)^n={}^n C_0 3^n+{}^n C_1 3^{n-1}+{}^n C_2 3^{n-2}+\cdots+{}^n C_{n-1} 3^{n-1}+{}^n C_n \\ \Rightarrow 4^n=\underset{r=0}{\overset{n}{\Sigma}} 3^r {}^n C_r
उपर्युक्त उदाहरणों के द्वारा द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11),कक्षा 11 में द्विपद प्रमेय (Binomial Theorem in Class 11) को समझ सकते हैं।
3.द्विपद प्रमेय किसी धन पूर्णांक n के लिए (Binomial Theorem for Any Positive Integer n):
उपपत्ति (Proof):इस प्रमेय की उपपत्ति गणितीय आगमन सिद्धान्त द्वारा प्राप्त की जाती है।
मान लीजिए कथन P(n) निम्नलिखित है:
P(n):(a+b)^n={}^n C_0 a^n-{}^n C_1 a^{n-1} b+{}^n C_2 a^{n-2} b^2+\ldots \ldots +{}^n C_{n-1}a b^{n-1}+{}^n C_n b^n
n=1 लेने परः
P(1):(a+b)^{1}={}^1 C_0 a^{\prime}+{}^1 C_1 b^{1}=a+b
अतः P(1) सत्य है।
मान लीजिए कि P(k), किसी धन पूर्णांक k के लिए सत्य है। अर्थात्
(a+b)^k={}^k C_0+{}^k C_1 a^{k-1} b+{}^k C_2 a^{k-2} b^2+\ldots+{}^k C_k b^k \ldots(1)
हम सिद्ध करेंगे कि P(k+1) भी सत्य है अर्थात्
(a+b)^{k+1}={}^{k+1} C_0 a^{k+1}+{}^{k+1} C_1 a^k b+{}^{k+1} C_2 a^{k+1} b^2 +\ldots \ldots+{}^{k+1} C_{k+1} b^{k+1}
अब, (a+b)^{k+1}=(a+b)(a+b)^k \\ =(a+b)\left({}^k C_0 a^k+{}^k C_1 a^{k-1} b+{}^k C_2 a^{k-2} b^2+\ldots+{}^k C_{k-1} a b^{k-1}+{}^k C_k b^k\right)[(1)से ]
={}^k C_0 a^{k+1}+{}^k C_1 a^k b+{}^k C_2 a^{k-1} b^2+ \ldots+{}^k C_{k-1} a^2 b^{k-1}+{}^k C_k a b^k+{}^k C_0 a^k b+{}^k C_1 a^{k-1} b^2+{}^k C_2 a^{k-2} b^2+\ldots+{}^k C_{k-1} a b^k+{}^k C_k a^k b^{k+1} [वास्तविक गुणा द्वारा]
={}^k C_0 a^{k+1}+\left({}^k C_1+{}^k C_2\right) a^k b+\left({}^k C_2+{}^k C_1\right) a^{k-1} b^{2}+\ldots \ldots+\left({}^k C_k+{}^k C_{k-1}\right) a b^k+{}^k C_k b^{k+1}(समान पदों के समूह बनाकर)
{}^{k+1} C_0 a^{k+1}+{}^{k+1} C_1 a^{k} b+{}^{k+1} C_2 a^{k-1} b^2+\ldots \ldots+{}^{k+1} C_k a b^k+{}^{k+1} C_{k+1} b^{k+1}
({}^{k+1} C_0=1, {}^k C_r+{}^k C_{r-1}={}^{k+1} C_r \text { और } {}^k C_k=1={}^{k+1} C_{k+1} का प्रयोग करके)
इससे सिद्ध होता है कि यदि P(k) भी सत्य है तो P(k+1) सत्य है।इसलिए,गणितीय आगमन सिद्धान्त द्वारा,प्रत्येक धन पूर्णांक n के लिए P(n) सत्य है।
4.द्विपद के प्रसार की कुछ विशिष्ट स्थितियाँ (Some Special Cases of Binomial Theorem):
(i) (a+b)^x में a=x तथा b=-y लेकर हम पाते हैं
(x-y)^n=[x+(-y)]^n \\ ={}^n C_0 x^n+{}^n C_1 x^{n-1}(-y)+{}^n C_2 x^{n-2}(-y)^2 +{}^n C_3 x^{n-3}(-y)^3+\ldots \ldots+ {}^n C_n (-y)^n \\ \Rightarrow (x-y)^n={}^n C_0 x^n-{}^n C_1 x^{n-1} y+{}^n C_2 x^{n-2} y^2+\ldots \ldots+(-1)^n \cdot {}^n C_n y^n
(ii)a=1 तथा b=x लेकर हम पाते हैं कि
(1+x)^n={}^n C_0 \cdot(1)^n+{}^n C_1 (1)^{n-1} x+{}^n C_2 (1)^{n-2} x^2+\cdots+{}^n C_n x^n \\ \Rightarrow (1+x)^n={}^n C_0+{}^n C_1x+{}^n C_2 x^2+{}^n C_3 x^3+\ldots \ldots+{}^n C_n x^n
(iii)a=1 तथा b=-x लेकर हम पाते हैं
(1-x)^n={}^n C_0-{}^n C_1 x+{}^n C_2 x^2- \ldots \ldots+(-1)^n {}^n C_n x^n
विशेषतः x=1 के लिए हम पाते हैं,
5.द्विपद प्रमेय कक्षा 11 पर आधारित सवाल (Questions Based on Binomial Theorem Class 11):
(1.)द्विपद प्रमेय से (2 x+3 y)^5 का प्रसार कीजिए।
(2.) \left(1+\sqrt{5}\right)^5+\left(1-\sqrt{5}\right)^5 का मान ज्ञात कीजिए।
उत्तर (Answers): (1.) 32 x^5+240 x^4 y+720 x^3 y^2+1080 x^2 y^3+810 x y^4+243 y^5 (2.)352
उपर्युक्त सवालों को हल करने पर द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11),कक्षा 11 में द्विपद प्रमेय (Binomial Theorem in Class 11) को ठीक से समझ सकते हैं।
Also Read This Article:- Permutations and Combinations Class 11
6.द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11),कक्षा 11 में द्विपद प्रमेय (Binomial Theorem in Class 11) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.पास्कल त्रिभुज किसे कहते हैं? (What is Pascal Triangle?):
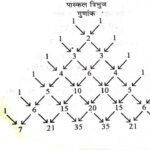
उत्तर:व्यंजक के प्रसार की जानकारी प्राचीन हिन्दु गणितज्ञों को थी।तीसरी शताब्दी ईस्वी पूर्व पिंगल ने गुणांकों के विन्यास का एक आरेख रूप प्रदान किया था,जिसे मेरूप्रस्त्र कहते थे।सोलहवीं शताब्दी में वामवेली ने भी (a+b)^n, n \leq 7 के तक के प्रसार के गुणांक ज्ञात किये थे।10 घात तक के गुणांकों की जानकारी भी सत्रहवीं शताब्दी के प्रारम्भ में आत्रेद ने दी थी।
इसके बाद फ्रांसीसी गणितज्ञ बी पास्कल (Blaise Pascal) ने द्विपद प्रसार के गुणांकों को ज्ञात करने के लिए एक त्रिभुज का निर्माण किया जिसको पास्कल त्रिभुज कहते हैं,जो निम्नलिखित प्रकार का है:
पास्कल त्रिभुज में प्रत्येक पंक्ति के प्रारम्भ और अन्त में 1 है।प्रारम्भ और अन्त में समान दूरी पर स्थित संख्याएँ बराबर है।किसी भी पंक्ति की कोई भी संख्या उससे ऊपर वाली पंक्ति की उन दो संख्याओं को जोड़ने से प्राप्त होती है,जो संख्या के बायें और दायें स्थित है।
प्रश्न:2.द्विपद प्रमेय की मुख्य बातें लिखिए। (Write the Main Points of Binomial Theorem):
उत्तर:(1.) {}^n C_0 a^n-{}^n C_1 a^{n-1} b+{}^n C_2 a^{n-2} b^2+\ldots \ldots +{}^n C_{n-1}a b^{n-1}+{}^n C_n b^n जहाँ b^0=1=a^{n-n} का संकेतन \underset{k=0}{\overset{n}{\Sigma}} {}^n C_k a^{n-k} b^k है।
अतः इस प्रमेय को इस प्रकार लिख सकते हैं।
(a+b)^n=\underset{k=0}{\overset{n}{\Sigma}} {}^n C_k a^{n-k} b^k
(2.)द्विपद प्रमेय में आनेवाले गुणांक को द्विपद गुणांक कहते हैं।
(3.) (a+b)^n के प्रसार में पदों की संख्या n+1 अर्थात् घातांक से 1 अधिक है।
(4.)प्रसार के उत्तरोत्तर पदों में,a की घातें एक क्रम से घट रही हैं।यह पहले पद में n, दूसरे पद में (n-1) और फिर इसी प्रकार अंतिम पद में शून्य है।ठीक उसी प्रकार b की घातें एक के क्रम से बढ़ रही हैं,पहले पद में शून्य से शुरू होकर,दूसरे पद में 1 और फिर इसी प्रकार अन्तिम पद में n पर समाप्त होती हैं।
(5.)(a+b)^n,के प्रसार में,a तथा b की घातों का योग,पहले पद में n+0=n,दूसरे पद में (n-1)+1=n और इसी प्रकार अन्तिम पद में 0+n=n है।अतः यह देखा जा सकता है कि प्रसार के प्रत्येक पद में a तथा b की घातों का योग n है।
प्रश्न:3.सी पी स्टेनमेट्ज के अनुसार गणित की परिभाषा दीजिए। (Define Mathematics According to C P STEINMETZ):
उत्तर:गणित एक सबसे सटीक विज्ञान है और इसके निष्कर्ष पूर्ण प्रमाणों में सक्षम हैं।-सी पी स्टीनमेट्ज़
(Mathematics is a most exact science and its conclusions are capable of absolute proofs.-C P STEINMETZ)
उपर्युक्त प्रश्नों के उत्तर द्वारा द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11),कक्षा 11 में द्विपद प्रमेय (Binomial Theorem in Class 11) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Binomial Theorem Class 11
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Binomial Theorem Class 11
द्विपद प्रमेय कक्षा 11
(Binomial Theorem Class 11)
Binomial Theorem Class 11
द्विपद प्रमेय कक्षा 11 (Binomial Theorem Class 11) द्वारा अधिक घात वाली संख्याओं
की गणना,क्रमिक गुणनफल की अधिक जटिल प्रक्रिया को दूर किया जा सकता है।








