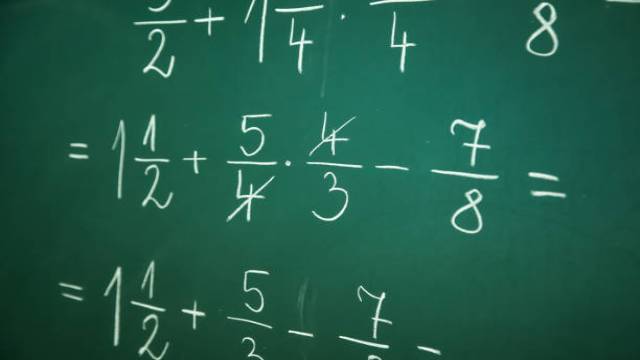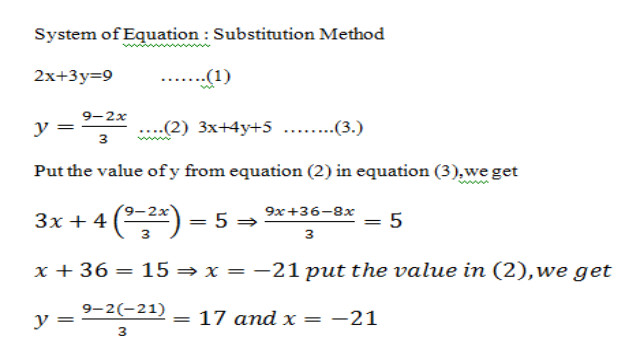Beginners Guide to Systems of Equations
समीकरणों के सिस्टम के लिए शुरुआती गाइड का परिचय (Introduction to Beginners Guide to Systems of Equations),Beginner’s Guide to Systems of Equations
- समीकरणों के सिस्टम के लिए शुरुआती गाइड (Beginners Guide to Systems of Equations) के द्वारा इस आर्टिकल में समीकरणों को हल करने की विधियों के बारे में बताया गया है.सामान्यत: रैखिक समीकर्णों को हल करने की पाँच विधियाँ क्रमश: विस्थापन विधि (Substitution Method),विलोपन विधि (Elimination Method),व्रजगुणन विधि (Cross Multiplication Method),ग्राफीय विधि (Graphical Method),तुलना विधि (Comparison Method) इत्यादि है.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Mathematics makes you moral
1.समीकरणों के सिस्टम के लिए शुरुआती गाइड (Beginners Guide to Systems of Equations):
- ओह, बुनियादी बातों। वे दुर्घटना से उन्हें मौलिक नहीं कहते हैं। और सबसे मौलिक बीजगणित अवधारणाओं में से एक सिस्टम ऑफ़ इक्वेशन हैं। तो अगर उन सभी के एक्स और वाई आपकी आँखों को पार कर रहे हैं, तो डरें नहीं। यह त्वरित मार्गदर्शिका आपको कुछ ही समय में सीधा कर देगी।
Also Read This Article:The man who invented modern probability
समीकरणों की समझ प्रणाली (Understanding Systems of Equations):
- इससे पहले कि आप उन अनजान लोगों के लिए सीखना सीखें, यह जानना महत्वपूर्ण है कि इन समाधानों का वास्तव में क्या मतलब है।
समीकरणों की एक प्रणाली क्या है? (What is a System of Equations?):
- समीकरणों की एक प्रणाली वास्तव में यह क्या कहती है। यह एक प्रणाली है, जिसका अर्थ है 2 या अधिक, समीकरण। जब आप पहली बार समीकरण समस्याओं का सामना करते हैं तो आप 2 रैखिक समीकरणों वाली समस्याओं को हल करेंगे। इसका मतलब है कि आपके समीकरणों में अधिकांश x- चर, y- चर और निरंतर मूल्य शामिल होंगे।
- आखिरकार (शायद बीजगणित 2, पूर्वकाल या रैखिक बीजगणित में) आप और अधिक जटिल प्रणालियों का सामना करेंगे। इनमें उच्च-क्रम के कार्य शामिल हो सकते हैं, जैसे कि क्वाडराटिक्स, सिस्टम में दो से अधिक समीकरण, या x, y और z चर वाले समीकरण (ये समीकरण 3D अंतरिक्ष में विमानों का प्रतिनिधित्व करते हैं)।
- लेकिन कोई फर्क नहीं पड़ता कि आपका सिस्टम कितना जटिल है, आपका समाधान हमेशा एक ही अवधारणा का प्रतिनिधित्व करता है: चौराहा। उदाहरण के लिए, दो रैखिक समीकरणों की एक प्रणाली का समाधान, सबसे सामान्य प्रकार की प्रणाली, दो पंक्तियों के बीच का चौराहा बिंदु है।
संभावित समाधान (Potential Solutions):
- जैसा कि आप पहले से ही महसूस कर सकते हैं, सभी लाइनें बिल्कुल एक बिंदु में प्रतिच्छेद नहीं करेंगी। परिभाषा के अनुसार समानांतर रेखाएं कभी भी प्रतिच्छेद नहीं करेंगी, इसलिए उनके पास कोई समाधान नहीं है। आप ऐसे समीकरणों का सामना भी कर सकते हैं जो अलग-अलग दिखते हैं, लेकिन जब कम हो जाते हैं तो समान समीकरण होते हैं। इस मामले में, आपके पास असीम रूप से कई समाधान होंगे।
Also Read This Article:System of linear equations
2.रेखांकन विधि (The Graphing Method):
- एक सिस्टम के चौराहे को खोजने का सबसे आसान और सबसे दृश्य तरीका समान समन्वय वाले विमान पर समीकरणों को रेखांकन करके है।
- रेखीय समीकरणों की एक प्रणाली को कैसे रेखांकन के साथ-साथ “कोई समाधान नहीं” और “असीम रूप से कई समाधान” के उदाहरणों को देखने के लिए नीचे दिए गए मेरे ट्यूटोरियल को देखें।
3.प्रतिस्थापन विधि (The Substitution Method):
- बेशक, समीकरणों की प्रणाली को हल करने के लिए रेखांकन सबसे कुशल तरीका नहीं है। इसीलिए हमारे बीजगणित शस्त्रागार में कुछ और तरीके हैं।
- पहला है प्रतिस्थापन विधि। इस विधि में, आप अपने एक समीकरण में एक चर को अलग करते हैं और उस रिश्ते को दूसरे समीकरण में प्लग करते हैं। यह आपको केवल एक चर के साथ एक समीकरण प्रदान करेगा, जिसका अर्थ है कि आप चर के लिए हल कर सकते हैं। एक बार जब आप एक चर का मूल्य जान लेते हैं, तो आप दूसरे चर का मूल्य आसानी से वापस हल करके पा सकते हैं।
- सबस्टीट्यूशन मेथड का उपयोग करके सिस्टम को कैसे हल करें, इस बारे में अधिक जानकारी के लिए, ऊपर ट्यूटोरियल को देखें।
3.उन्मूलन विधि (The Elimination Method):
- यदि प्रतिस्थापन विधि आपके कप चाय के साथ नहीं है, तो आपके पास अपने निपटान में एक अंतिम विधि है: उन्मूलन विधि।
- इस विधि में, आप दोनों समीकरणों को एक साथ जोड़कर एक चर को रणनीतिक रूप से समाप्त कर देंगे। ऐसा करने के लिए, किसी चर को समाप्त करने के लिए आपको अक्सर एक या दोनों समीकरणों को एक मूल्य से गुणा करना होगा। एक बार जब आप समीकरण जोड़ लेते हैं और एक चर को समाप्त कर देते हैं, तो आपको उस समीकरण के साथ छोड़ दिया जाएगा जिसमें केवल एक प्रकार का चर है। जो आसान है क्योंकि आप उस चर के लिए हल कर सकते हैं। एक बार जब आप एक चर के लिए हल करते हैं तो आप दूसरे चर के मूल्य को खोजने के लिए मूल समीकरणों में से एक में परिणाम कर सकते हैं।वास्तव में यह कैसे काम करता है, के माध्यम से टहलने के लिए, एक प्रणाली को हल करने के लिए उन्मूलन विधि का उपयोग करने पर मेरे ऊपर उदाहरण को देखें।
और यह आपका समीकरणों के सिस्टम से परिचय है। समीकरणों के अधिक उन्नत सिस्टम को हल करने के तरीके के बारे में अधिक जानकारी के लिए, जिसमें बैक-सॉल्विंग और मैट्रिसेस का उपयोग करके तीन समीकरणों के सिस्टम को कैसे हल किया जाए. - उपर्युकत आर्टिकल में समीकरणों के सिस्टम के लिए शुरुआती गाइड (Beginners Guide to Systems of Equations) के बारे में बताया गया है.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |