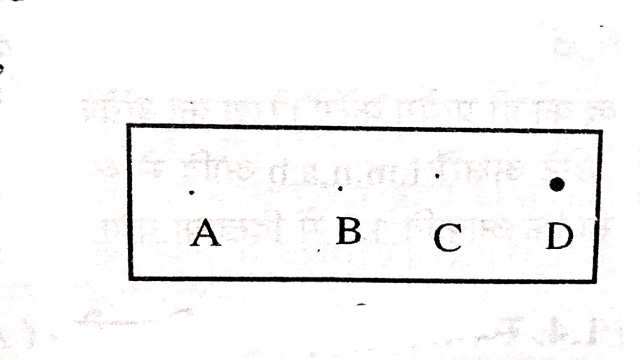Basic Concepts of Geometry Class 9
1.ज्यामिति की मौलिक संकल्पनाएँ कक्षा 9 (Basic Concepts of Geometry Class 9),ज्यामिति की मौलिक संकल्पनाएँ (Basic Concepts of Geometry):
- ज्यामिति की मौलिक संकल्पनाएँ कक्षा 9 (Basic Concepts of Geometry Class 9) में शब्द ‘ज्यामिति’ यूनानी भाषा के दो शब्दों ‘जियो’ (geo) और ‘मेट्रन’ (metrein) से बना है।’जियो’ का अर्थ ‘भूमि’ और ‘मेट्रन’ का अर्थ है ‘मापना’।हिंदी में इसे ज्यामिति या भूमिति कहते हैं। प्राचीनकाल में सभ्यता के विकास के साथ-साथ भूमि क्षेत्रों के मापन की आवश्यकता हुई तब गणित की इस शाखा का विकास हुआ।गणित की इस शाखा के अंतर्गत बिंदुओं,रेखाओं,रैखिक आकृतियों,तलों और ठोस पिण्डों के आकार,विस्तार और गुणों का अध्ययन किया जाता है।
- गणित के इतिहास एवं शास्त्रों से ज्ञात होता है कि मिस्र निवासियों ने सर्वप्रथम ज्यामिति का अध्ययन किया था जिसमें क्षेत्रमिति की समस्याएं प्रमुख थी।इसके पश्चात बेबीलोन निवासियों ने भी विभिन्न रैखिक आकृतियों का क्षेत्रफल ज्ञात करने की समस्याओं का अध्ययन किया।बेबीलोन निवासियों के पुराने गणित शास्त्र में ‘रिहण्ड पेपिरस’ (Rhind papyrus,1050 ईसा पूर्व) में क्षेत्रफल ज्ञात करने संबंधी सूत्र मिलते हैं।प्राचीन भारत (2500 ईसा पूर्व से 1750 ईसा पूर्व) में पनपी सभ्यता के अवशेषों से पता चलता है कि उन्हें ज्यामिति का काफी ज्ञान था।भारतीय लोग ज्यामिति का उपयोग सड़क और मकान बनाने में किया करते थे।वैदिक काल (800 ईसा पूर्व से 500 ईसा पूर्व तक) में,वैदिक पूजार्थ निर्मित वेदियों और अग्नि कुण्डों के निर्माण में प्रयुक्त सुल्व सूत्रों (sulba sutras) का उल्लेख मिलता है।’सुल्व’ यानि रस्सी (एक लंबाई का माप) और सुल्व सूत्र यानि रस्सी द्वारा मापने का सूत्र।
- ‘बौद्धायन सुल्व सूत्र’ (800 ईसा पूर्व) में पाइथागोरस प्रमेय का स्पष्ट वर्णन मिलता है।ज्यामिति का यह ज्ञान मिश्र निवासियों से यूनानियों तक पहुंचा।’मिलेटस’ नामक नगर के एक व्यापारी थेल्स (Thales of Miletus) (640 ईसा पूर्व से 546 ईसा पूर्व तक) ने ज्यामिति के प्रति रुचि दिखाई।इस धनी व्यापारी ने ज्यामिति का अध्ययन कर इसका ज्ञान अपने शिष्यों को दिया।पाइथागोरस (Pythagoras) (580 ईसा पूर्व से 500 ईसा पूर्व तक) थेल्स के प्रसिद्ध शिष्य थे।पाइथागोरस ने ज्यामिति के बहुत से महत्त्वपूर्ण तथ्यों को सिद्ध किया।
- भारत के गणितज्ञों आर्यभट (476 ईस्वी),ब्रह्मगुप्त (जन्म 598 ईस्वी) और भास्कर-II (जन्म 1114 ईस्वी) का उल्लेख ज्यामिति के कार्यक्षेत्र में मिलता है।आर्यभट (Aryabhatt) ने समद्विबाहु त्रिभुज का क्षेत्रफल एवं पिरैमिड का आयतन ज्ञात करना बताया।ब्रह्मगुप्त (Brahmagupta) ने चक्रीय चतुर्भुज का क्षेत्रफल,उसकी भुजाओं और अर्द्ध परिमाप के रूप में ज्ञात किया।भास्कर-II ने पाइथागोरस प्रमेय की उत्पत्ति विच्छेदन विधि द्वारा दी।
- आज हम समतल ज्यामिति का जिस रूप में अध्ययन कर रहे हैं,उसे लगभग दो हजार तीन सौ वर्ष पूर्व यूनान के गणितज्ञ यूक्लिड (Euclid) (300 ईसा पूर्व) ने गहन अध्ययन कर उसके तथ्यों को निगमनिक तर्क द्वारा सिद्ध करते हुए,क्रमबद्ध रूप से व्यवस्थित कर अपने विशाल कार्य को ‘एलिमेंटस'(Elements) नामक ग्रंथ में प्रकाशित किया।इस ग्रंथ के तेरह खण्ड हैं।यूक्लिड को ज्यामिति का पिता कहा जाता है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Non Euclidean Geometry
2.ज्यामिति के अध्ययन का महत्त्व (Importance of Study of Geometry):
- इससे पूर्व भी हम एक समतल में ज्यामितीय आकृतियों को बनाकर विभिन्न तथ्यों की जानकारी प्राप्त कर चुके हैंः
- (i)त्रिभुज के तीनों कोणों का योग 180 डिग्री के बराबर होता है।
- (ii)दो समांतर रेखाओं को एक तिर्यक रेखा काटे तो संगत कोण बराबर होते हैं।
- इस प्रकार केवल आकृति बनाकर रेखाखंड या कोण मापकर तथ्यों की जाँच करना व उन्हें याद करना कठिन कार्य लगता है।इस कार्य को सरल बनाने के लिए ज्यामितिविदों ने कुछ आधारभूत तथ्यों को सत्य मानकर,अन्य तथ्यों को उनसे तर्क द्वारा सिद्ध किया।इस प्रकार विद्यार्थियों में तर्क आधारित सोच विकसित कर परिणामों को खोजने एवं निष्कर्ष ज्ञात करने के लिए ज्यामिति अध्ययन उपयोगी है।ज्यामिति अध्ययन का प्रायोगिक महत्त्व हमारे परिवेश में दृष्टिगोचर होता ही है इसके अलावा विभिन्न विषयों में इसकी उपयोगिता है।
3.बिंदु,रेखा और समतल (Point Line and Plane):
- रेखागणित में तीन मौलिक कल्पनाएं हैंःबिन्दु,रेखा और समतल।इन्हें ठीक-ठीक परिभाषित करना संभव नहीं है।किंतु उदाहरणों की सहायता से इन संकल्पनाओं को हम समझ सकते हैं।किसी चिकनी दीवार की सतह,चिकने ब्लैक बोर्ड की सतह,कागज के पन्ने की सतह और कमरे का चिकना फर्श ज्यामिति के ‘समतल’ (plane) के मिलते जुलते उदाहरण हैं।इन उपर्युक्त सतहों की सीमाएं होती हैं परंतु ज्यामिति का ‘समतल’ दिशाओं में अनंत तक फैला हुआ होता है।समतल लंबाई और चौड़ाई में फैला हुआ होता है इसकी मोटाई नहीं होती है।
- यदि हम कागज के एक पन्ने पर पेन्सिल की बारीक नोंक द्वारा एक ‘सूक्ष्म चिन्ह’ लगावें तो यह रेखागणित के एक बिंदु (point) से काफी मिलता-जुलता होगा।रेखागणित का बिंदु समतल में एक स्थिति बताने के लिए एक सूक्ष्म चिन्ह है जिसका कोई आकार नहीं होता,ऐसा माना जाता है।अतः पेंसिल की नोंक जितनी अधिक बारीक होगी उसके द्वारा लगाया गया चिन्ह भी उतना ही रेखागणित के बिंदु की कल्पना के निकट होगा।बिंदु को अंग्रेजी वर्णमाला के बड़े अक्षरों A,B,C,P,Q,R आदि से व्यक्त करते हैं।
- आकृति में अंकित चिन्ह A,B एवं C रेखागणित के बिंदु माने जाते हैं किंतु D नहीं।D का आकार बड़ा होने के कारण इसे एक संख्या कहा जाता है।
- यदि आप एक बारीक नोंक वाली पेन्सिल लेकर,नोंक को एक स्केल (scale) या पैमाने के सहारे-सहारे कागज के एक तल पर चलाएं।इस प्रकार की आकृति बनेगी तो वह ज्यामिति की एक ‘सरल रेखा’ (straight line) का मिलता-जुलता उदाहरण होगा।आपने दैनिक जीवन में दो समतलों के मिलने पर बनी कोरों को देखा होगा।ये कोरे भी ज्यामिति की सरल रेखा के मिलते जुलते उदाहरण हैं।दो दीवारों के मिलने से बनी कोर को ऊपर आसमान में एवं नीचे जमीन में,जितना चाहे बढ़ाया जा सकता है।इसी प्रकार कागज के पन्ने पर पेंसिल की बारीक नोंक से खींची गई सरल रेखा को जितना चाहें दोनों ओर बढ़ाया जा सकता है।अतः ज्यामिति की सरल रेखा दोनों ओर लंबाई में अनन्त तक बढ़ी हुई मानी जाती है।इसकी चौड़ाई और मोटाई नहीं होती है।इस लेख में सरल रेखा के स्थान पर हम रेखा शब्द का ही प्रयोग करेंगे।
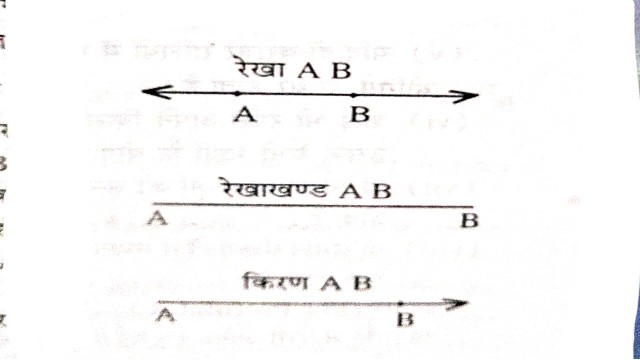
- एक रेखा पर स्थित कोई बिन्दु A तथा B हैं तो उसे रेखा \overleftrightarrow{AB} द्वारा व्यक्त किया जाता है।यदि रेखा दोनों ओर बिंदुओं A और B से सीमित हो तो रेखाखंड AB या \overline{AB} कहा जाता है।रेखाखण्ड की एक निश्चित लंबाई होती है।अतः \overline{AB}=\overline{BA} होता है।यदि रेखा एक तरफ A से सीमित हो और दूसरी तरफ बिन्दु B की ओर बढ़ी हुई हो तो उसे किरण AB या \overrightarrow{AB} कहा जाता है।
- कल्पना कीजिए कि एक सरल रेखा,रेखाखंड अथवा किरण पर कितने बिन्दु स्थित हो सकते हैं?आपका उत्तर होगा अनगिनत।
- अतः ज्यामिति की एक सरल रेखा,किरण या रेखाखण्ड को उन अनन्त बिन्दुओं के समुच्चय के रूप में माना जा सकता है जो कि एक सीध में व्यवस्थित हो।
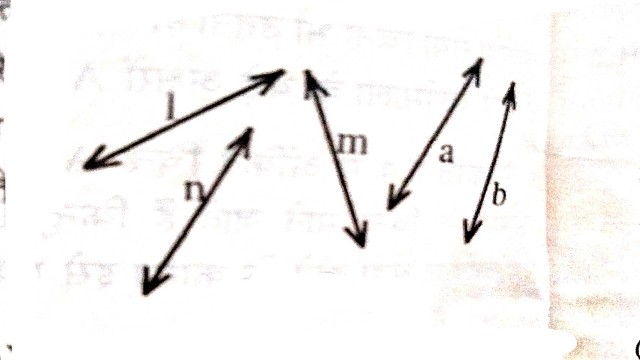
- इस लेख में जब तक कोई विशेष स्थिति न हो हम रेखा,किरण और रेखाखंड के लिए रेखा शब्द का ही प्रयोग करेंगे।रेखा को अंग्रेजी वर्णमाला के छोटे अक्षरों l,m,n,a,b आदि से व्यक्त करते हैं जैसा की आकृति में दिखाया गया है।
4.स्वयंसिद्ध और अभीगृहीत (Axioms and Postulates):
- स्वयंसिद्ध (Axioms):गणित में हम देखते हैं कि अनेक तथ्य इतने सरल एवं स्पष्ट होते हैं कि इन्हें अनुभव के आधार पर सत्य मान सकते हैं।अतः वह सरल और स्पष्ट सिद्धांत जिनकी सत्यता सिद्ध करने की आवश्यकता नहीं होती और जिनको बिना सिद्ध किए ही हम सत्य मान लेते हैं,स्वयंसिद्ध कहलाते हैं।नीचे कुछ स्वयंसिद्ध दिए गए हैंः
- (i)एक कथन या तो सत्य होता है या असत्य।
- (ii)एक राशि,दूसरी राशि के बराबर,बड़ी अथवा छोटी होती है।
- (iii)वे राशियाँ जो एक ही राशि के समान हों,परस्पर समान होती हैं।
- (iv)यदि समान राशियों को,दो समान राशियों में जोड़ा जाए तो योगफल समान होता है।
- (v)यदि दो बराबर राशियों में से दो बराबर राशियां घटाई जाए तो उनका अंतर भी बराबर होता है।
- (vi)कोई भी राशि अपने किसी भाग से कम नहीं होती अर्थात् संपूर्ण राशि उसके सभी भागों के योग के तुल्य होती है।
- (vii)दो समान संख्याओं को समान संख्या से गुणा करने पर गुणनफल समान प्राप्त होता है।
- (viii)दो समान संख्याओं समान (अशून्य) संख्या का भाग देने पर भागफल समान प्राप्त होता है।
अभीगृहीत (Postulates):ज्यामिति में अनेक रचनाएँ देखने को मिलती है जिन्हें बिना प्रमाण के सम्भव मान ली जाती हैं और इनके आधार पर अन्य ज्यामितीय रचनाओं या तथ्यों को सिद्ध किया जाता है।ऐसी अनेक रचनाएँ जिन्हें बिना प्रमाण के प्रारंभिक तौर पर सत्य स्वीकार कर लिया जाता है,अभीगृहीत कहलाते हैं।कुछ अभीगृहीत निम्नानुसार हैंः
(1.)बिंदु और रेखाएं संबंधी अभीगृहीत (Postulates Related to Points and Lines): - (i)एक रेखा पर अनंत बिंदु होते हैं।
- (ii)एक रेखाखंड को अपनी इच्छानुसार कितनी ही लंबाई तक बढ़ाया जा सकता है।
- (iii)एक दिए गए बिंदु से अनंत रेखाएं खींची जा सकती हैं।
- (iv)दो बिंदुओं से गुजरती हुई एक और केवल एक ही सरल रेखा खींची जा सकती हैं।
- (v)दो बिंदुओं के बीच का न्यूनतम मार्ग उन बिंदुओं को मिलाने वाला रेखाखंड होता है।
(2.)समांतर रेखाएं संबंधी अभीगृहीत (Postulates Related to Parallel Lines): - (i)एक दी गई रेखा के समांतर,किसी बाह्य बिंदु से एक और केवल एक ही रेखा खींची जा सकती है।
- (ii)जब दो समांतर रेखाओं को एक तिर्यक रेखा काटे तो संगत कोण बराबर होते हैं।
(3.)कोण संबंधित अभीगृहीत (Postulates Related to Angles): - (i)सभी समकोण बराबर होते हैं।
- (ii)समान पूरक कोण वाले कोण आपस में बराबर होते हैं।
- (iii)समान सम्पूरक वाले कोण आपस में बराबर होते हैं।
(4.)विविध अभीगृहीत (Various Postulates): - (i)एक रेखाखंड को एक और केवल एक ही बिंदु पर समद्विभाजित किया जा सकता है।
- (ii)एक कोण को एक और केवल एक ही रेखा द्वारा समद्विभाजित किया जा सकता है।
- (iii)एक दी गई आकृति को दूसरे स्थान पर बिना रूप तथा आकार बदले रखा जा सकता है या बनाया जा सकता है।
- (iv)जब दो रेखाखंड समान हों तो उनके अंत्य बिंदुओं को एक दूसरे से ठीक-ठीक मिलाया जा सकता है।अर्थात् एक रेखाखंड दूसरे को ठीक-ठीक ढक लेगा।
- (v)यदि दो कोण समान हों तो उनके शीर्ष व कोण को ठीक-ठीक मिलाया जा सकता है।
Also Read This Article:Euclid Geometry Class 9
5.आगमनिक और निगमनिक तर्क (Inductive and Deductive Reasoning):
- गणित में विभिन्न नियम,प्रायोगिक तौर पर विभिन्न उदाहरणों से सामान्य निष्कर्ष निकालकर स्थापित किए जाते हैं,इस प्रकार स्थापित नियमों को आगमन विधि द्वारा स्थापित कहा जाता है।ऐसे निष्कर्षों में हमेशा यह शंका बनी रहती है कि क्या ये निष्कर्ष सभी स्थितियों में सत्य हैं अथवा नहीं।अतः एक नियम को सिद्ध करने के लिए एक विशेष प्रकार की तर्क विधि जिसमें क्रमशः चरणबद्ध तरीके से कथन का प्रमाण देते हुए कि “यह सही है अतः वह सही है” का उपयोग कर गणितीय निष्कर्ष की सत्यता सिद्ध की जाती है।
- इस प्रकार की तर्क विधि निगमनिक तर्क विधि कहलाती है।निगमनिक तर्क विधि में निम्न प्रक्रिया अपनाते हैंः
- (i)स्वीकार किए गए कथनो से प्रारंभ करना।(स्वयंसिद्ध या अभीगृहीत)
- (ii)शर्ते निर्धारित करना।
- (iii)तार्किक कारणों का उपयोग करना।
- (iv)निष्कर्ष ज्ञात करना।
6.प्रमेय और निर्मेय (Theorems and Problems):
- समतल ज्यामिति अध्ययन को दो भागों में बांटा गया हैः
- (i)सैद्धान्तिक ज्यामिति
- (ii)क्रियात्मक ज्यामिति
- सैद्धान्तिक ज्यामितिःसैद्धान्तिक ज्यामिति में कथन की सत्यता को क्रमागत तर्कों से सिद्ध किया जाता है।
क्रियात्मक ज्यामितिःक्रियात्मक ज्यामिति में ज्यामितीय आकृतियों की रचनाएं की जाती है।
गणित के विद्वान प्रत्येक ज्यामितीय विचार को चाहे वह सैद्धांतिक हो या क्रियात्मक,साध्य (Propositions) कहते हैं।साध्य दो प्रकार के होते हैंः(i)प्रमेय (Theorem) (ii)निर्मेय (Problem) - प्रमेय (Theorem):निगमनिक तर्क विधि द्वारा सत्यापित निष्कर्षों को प्रमेय कहा जाता है।
निर्मेय (Problem):ज्यामितीय नियमों का उपयोग कर की गई ज्यामितीय रचना को निर्मेय कहते हैं।
7.ज्यामिति के आगमन की विधि (Method of Study of Geometry):
- प्रमेय तथा निर्मेय का अध्ययन आगमनिक,निगमनिक तथा वैश्लेषिक (Analytic) विधि से किया जाता है।इस विधि में प्रत्येक प्रमेय को क्रमागत पदों में लिखा जाता है,प्रत्येक कथन की सत्यता के लिए आवश्यक प्रमाण दिए जाते हैं।ज्यामिति में किसी प्रमेय को सिद्ध करने के लिए निम्नलिखित चरणों का उपयोग किया जाता हैः
- (i)सर्वप्रथम प्रमेय लिखते हैं जो कि एक सामान्य कथन के रूप में होता है।इस कथन का एक भाग परिकल्पना और दूसरा भाग निष्कर्ष होता है।
- (ii)परिकल्पना के अनुसार आकृति बनाई जाती है।
- (iii)”दिया हुआ है” (Given) शीर्षक के अंतर्गत प्रमेय की परिकल्पना को आकृति द्वारा स्पष्ट करके लिखा जाता है।
- (iv)”सिद्ध करना है” (To Prove) शीर्षक के अंतर्गत शीर्षक के अन्तर्गत,प्रमेय के निष्कर्ष को जो कि हमें सिद्ध करना होता है,आकृति के अनुसार लिखा जाता है।
- (v)”रचना” (Construction) शीर्षक के अंतर्गत प्रमेय को सिद्ध करने हेतु आवश्यक रचना करनी हो तो उसे आकृतिनुसार स्पष्टतया लिखा जाता है।
- (vi)”उपपत्ति” (Proof) शीर्षक के अंतर्गत क्रमशः कथन और कारण स्पष्ट करते हुए प्रमेय को चरणबद्ध तरीके से सिद्ध किया जाता है।अंत में जब प्रमेय सिद्ध हो जाता है तो Q.E.D. (Quod erat demon strandum) या इतिसिद्धम अंकित किया जाता है,जिसका अर्थ है कि सिद्ध किया जा चुका है।
8.समांतर एवं प्रतिच्छेदी रेखाएं (Parallel and Intersecting Lines):
- समांतर रेखाएंःयदि एक समतल में दो रेखाएं खींची जाएं और वे इस प्रकार से हों कि उन्हें आगे या पीछे कितना ही बढ़ाने पर भी वे आपस में कहीं न मिले तो ऐसी रेखाएं समांतर रेखाएं कही जाती है।
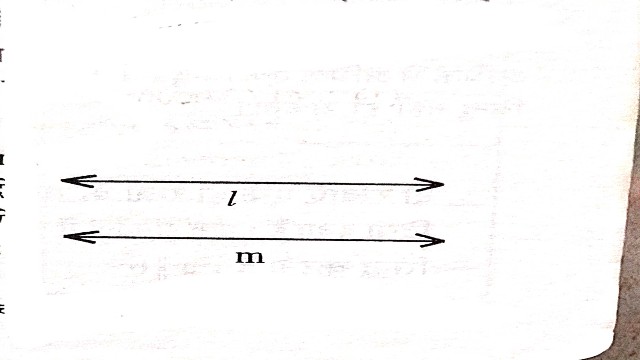
- यदि एक रेखा को अनंत बिंदुओं का समुच्चय मानें तो यह कहा जा सकता है कि दो रेखाओं में कोई उभयनिष्ठ बिन्दु नहीं होता।आकृति में l और m दो समान्तर रेखाएं हैं।
- प्रतिच्छेदी रेखाएँःयदि समतल में खींची गई दो रेखाएँ इस प्रकार हों कि वे आपस में समांतर नहीं हैं तो उन्हें प्रतिच्छेदी रेखाएं कहा जाता है।
- क्या प्रतिच्छेदी रेखाओं में एक ही उभयनिष्ठ बिन्दु होता है या अधिक? इसकी जानकारी निम्न प्रमेय से मिलती है,इस प्रमेय के अनुसार दो प्रतिच्छेदी रेखाओं में एक से अधिक उभयनिष्ठ बिन्दु नहीं हो सकते।
- अतः हम कह सकते हैं कि प्रतिच्छेदी रेखाएँ एक ही बिन्दु पर प्रतिच्छेद करती हैं और इस उभयनिष्ठ बिन्दु को प्रतिच्छेद बिन्दु कहते हैं।आकृति में रेखाएँ a और b प्रतिच्छेदी रेखाएँ हैं।बिन्दु ‘O’ प्रतिच्छेद बिन्दु है।
- उपर्युक्त आर्टिकल में ज्यामिति की मौलिक संकल्पनाएँ कक्षा 9 (Basic Concepts of Geometry Class 9),ज्यामिति की मौलिक संकल्पनाएँ (Basic Concepts of Geometry) के बारे में बताया गया है।
9.छात्र के दाढ़ी मूछ में ब्रेक (हास्य-व्यंग्य) (Student’s Beard and Moustache) (Humour-Satire):
- एक विद्यार्थी मोटरसाइकिल पर सवार होकर,शहर की बड़ी-बड़ी इमारतों को देखते हुए सामने से एक महिला से टकरा गया।
- महिलाःअरे तेरे इतनी बड़ी-बड़ी मूँछ और दाढ़ी आ गई है और गाड़ी देखकर नहीं चला सकता,जो तूने मेरे टक्कर मार दी।
- छात्रःआंटी जी,क्या मेरे मूंछ और दाढ़ी में ब्रेक लग रहे हैं जो गाड़ी को रोक देते।
10.ज्यामिति की मौलिक संकल्पनाएँ कक्षा 9 (Frequently Asked Questions Related to Basic Concepts of Geometry Class 9),ज्यामिति की मौलिक संकल्पनाएँ (Basic Concepts of Geometry) से संबंधित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.उपप्रमेय से क्या तात्पर्य है? (What Do You Mean by Corollaries?):
उत्तर:कभी-कभी जब किसी प्रमेय को सिद्ध कर लेते हैं तो उससे कुछ ऐसे परिणाम निकल आते हैं जिन्हें आसानी से समझा जा सकता है।ऐसे परिणामों को उपप्रमेय (Corollaries) कहते हैं।
प्रश्न:2.प्रमेय का विलोम से क्या तात्पर्य है? (What Do You Mean by the Converse of a Theorem?):
उत्तर:यदि दो प्रमेय इस प्रकार हैं कि प्रत्येक की परिकल्पना दूसरे का परिमाण है तो वे एक दूसरे का विलोम (converse) कहलाते हैं।यह आवश्यक नहीं है कि प्रत्येक प्रमेय का विलोम प्रमेय हो।
प्रश्न:3.कोण किसे कहते है? (What is Angle?):
उत्तर:कोई भी दो किरण जिनका बिंदु एक ही हो कोण बनाती है।
प्रश्न:3.कोण किसे कहते है? (What is Angle?):
उत्तर:कोई भी दो किरण जिनका बिंदु एक ही हो कोण बनाती है।
- उपर्युक्त प्रश्नों के उत्तर द्वारा ज्यामिति की मौलिक संकल्पनाएँ कक्षा 9 (Basic Concepts of Geometry Class 9),ज्यामिति की मौलिक संकल्पनाएँ (Basic Concepts of Geometry) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.