Assignment Problems in Optimization

Q: प्रश्न:3.नियतन समस्या का गणितीय गठन लिखिए। (Write Mathematical Formulation of Assignment Problem):

उत्तर:यदि (if) x_{ij}=X_{i j}, Z=\underset{i=1}{\overset{n}{\sum}} \underset{j=1}{\overset{n}{\sum}} c_{i j}, x_{i j} को प्रत्येक x_{i j} के लिए न्यूनतम (minimize) करता है,तथा साथ ही \underset{i=1}{\overset{n}{\sum}} x_{ij}=1=\underset{j=1}{\overset{n}{\sum}} x_{ij} तथा x_{i j} \geq 0 तब x_{ij}=X_{i j} , Z^{\prime}=\underset{i=1}{\overset{n}{\sum}} \underset{j=1}{\overset{n}{\sum}} c^{\prime}_{i j}, x_{i j} को भी न्यूनतम करता है। जहाँ C^{\prime}_{i j}=c_{i j} \pm a_i \pm b_j, i, j=1,2, \ldots n एवं a_{i} तथा b_{j} अचर हैं। उपर्युक्त प्रश्नों के उत्तर द्वारा इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।

Mathematics Satyam September 3, 2024 Linear Programming No Comments

Contents hide

1 1.इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems):

1.1 2.इष्टतमीकरण में नियतन समस्याएं पर आधारित उदाहरण (Illustrations Based on Assignment Problems in Optimization):

1.2 3.इष्टतमीकरण में नियतन समस्याएं पर आधारित सवाल (Questions Based on Assignment Problems in Optimization):

1.2.1 4.इष्टतमीकरण में नियतन समस्याएं (Frequently Asked Questions Related to Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.निर्दिष्ट कलन विधि के मुख्य पद लिखिए। (Write Down the Main Steps of a Assignment Algorithm):

1.2.3 प्रश्न:2.शून्य निर्दिष्टीकरण से आपका क्या आशय है? (What Do You Mean by Zero Assignment?):

1.2.4 प्रश्न:3.नियतन समस्या का गणितीय गठन लिखिए। (Write Mathematical Formulation of Assignment Problem):

1.2.4.1 Assignment Problems in Optimization

2 इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization)

2.1 Assignment Problems in Optimization

1.इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems):

Assignment Problems in Optimization

इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization) के इस आर्टिकल में हम विशेष प्रकार की समस्याओं पर आधारित सवालों को हल करेंगे जिन्हें नियतन तथा अधिन्यासन समस्यायें कहते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:- Assignment Problems

2.इष्टतमीकरण में नियतन समस्याएं पर आधारित उदाहरण (Illustrations Based on Assignment Problems in Optimization):

Illustration:6.निम्न नियतन समस्या हल कीजिए:
(Solve the following assignment problem):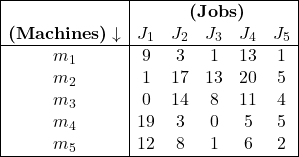
$\begin{array}{|c|ccccc|} \hline & \multicolumn{5}{|c|}{\textbf{कार्य (Jobs)}} \\ \textbf{मशीन(Machines)} \downarrow & J_1 & J_2 & J_3 & J_4 & J_5 \\ \hline m_1 & 9 & 3 & 1 & 13 & 1 \\ m_2 & 1 & 17 & 13 & 20 & 5 \\ m_3 & 0 & 14 & 8 & 11 & 4 \\ m_4 & 19 & 3 & 0 & 5 & 5 \\ m_5 & 12 & 8 & 1 & 6 & 2 \\ \hline \end{array}$
Solution:पद (step):I.प्रत्येक पंक्ति के न्यूनतम अवयव को उसी पंक्ति के प्रत्येक अवयव में से घटाने पर पंक्ति समानयन निम्न मैट्रिक्स प्राप्त होती है:
सारणी 1

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 8 & 2 & 1 & 12 & 0 \\ m_2 & 0 & 16 & 12 & 19 & 4 \\ m_3 & 0 & 14 & 8 & 11 & 4 \\ m_4 & 19 & 3 & 0 & 5 & 5 \\ m_5 & 11 & 7 & 0 & 5 & 1 \\ \cline{2-6} \end{array}$
पद (step):II.सारणी के प्रत्येक स्तम्भ के न्यूनतम अवयव को उसी स्तम्भ के प्रत्येक अवयव में से घटाने पर स्तम्भ समानयन निम्न मैट्रिक्स प्राप्त होती है:
सारणी 2

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 8 & 0 & 0 & 7 & 0 \\ m_2 & 0 & 14 & 12 & 14 & 4 \\ m_3 & 0 & 12 & 8 & 6 & 4 \\ m_4 & 19 & 1 & 0 & 0 & 5 \\ m_5 & 11 & 5 & 0 & 0 & 1\\ \cline{2-6} \end{array}$
पद (step):III.शून्य नियतन (निर्दिष्टीकरण) प्रथम पंक्ति से अवलोकन प्रारम्भ करते हुए उन पंक्तियों को चुनते हैं जिनमें एक और केवल एक शून्य हो।यहाँ दूसरी पंक्ति ऐसी है।इस पंक्ति के शून्य को $(\square)$ से अंकित करते हैं तथा इस शून्य से होकर जाने वाले स्तम्भ की अन्य सभी शून्यों को काट (×) देते हैं।पुनः प्रथम स्तम्भ से अवलोकन प्रारम्भ करते हुए उन स्तम्भों को चुनते हैं जिनमें अचिन्हित एक और केवल एक शून्य हो।यहाँ ऐसा स्तम्भ द्वितीय है इस स्तम्भ की शून्य को वर्ग $(\square)$ से अंकित करते हैं और इस शून्य से होकर जानेवाली पंक्ति की अन्य शून्य को काट (×) देते हैं।इस प्रकार सारणी में यह नियतन निम्नानुसार है:
सारणी 3

$\begin{array}{cccccc} & \quad \quad J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \hline m_1 & 8 & \fbox{0} & \xcancel{0} & 7 & \xcancel{0} \\ m_2 & \fbox{0} & 14 & 12 & 14 & 4 \\ m_3 & \xcancel{0} & 12 & 8 & 6 & 4 \\ m_4 & 19 & 1 & 0 & 0 & 5 \\ m_5 & 11 & 5 & 0 & 0 & 1\\ \hline \end{array}$
पद (step):IV.अब समस्त शून्यों को कम से कम एक बार रेखाओं से ढकने के लिए न्यूनतम संख्या में रेखाएँ खींचते हैं जिसकी विधि निम्न प्रकार है:
सारणी 4

$\begin{array}{c|ccccc|c} & (6)& & (4) & (5) & & \\ & J_1 & J_2 & J_3 & J_4 & J_5 & \\ \cline{2-6} m_1 & 8 \cdots & \fbox{0} \cdots & \xcancel{0} \cdots & 7 \cdots & \xcancel{0} \cdots & \\ & \vdots & & \vdots & \vdots & & \\ m_2 & \fbox{0} & 14 & 12 & 14 & 4 & (7)\\ & \vdots & & \vdots & \vdots & & \\ m_3 & \xcancel{0} & 12 & 8 & 6 & 4 & (1)\\ & \vdots & & \vdots & \vdots & & \\ m_4 & 19 & 1 & 0 & 0 & 5 & (2) \\ & \vdots & & \vdots & \vdots & & \\ m_5 & 11 & 5 & 0 & 0 & 1 & (3)\\ \cline{2-6} \end{array}$
(i)सारणी 3 को पुनः बनाइये।
(ii)पंक्ति 3,4,5 को चिन्हित $(\checkmark)$ कीजिए क्योंकि इसमें नियतन नहीं है।
(iii)पंक्ति 3,4 व 5 के स्तम्भ 1,3 तथा 4 में शून्य हैं इसलिए स्तम्भ 1,3 तथा 4 को चिन्हित $(\checkmark)$ कीजिए।
(iv)चिन्हित $(\checkmark)$ स्तम्भ 1 की पंक्ति 2 में वर्ग $(\square)$ अंकित है,को चिन्हित $(\checkmark)$ कीजिए।
पद (step):V.अब हम सभी चिन्हित स्तम्भों 1,3 तथा 4 से रेखाएँ खींचते हैं।फिर अचिन्हित पंक्ति 1 जिनमें शून्य है परन्तु उससे कोई रेखा नहीं गुजरती पर रेखा खींचते हैं।अब क्योंकि कोई ऐसी शून्य शेष नहीं है जिस पर रेखा नहीं गुजरती।
मैट्रिक्स का क्रम 5×5 है परन्तु रेखाओं की संख्या 4 है इसलिए इससे इष्टतम हल प्राप्त नहीं हो सकता।
पद (step):VI.अब उन सभी अवयवों जो रेखाओं से ढके नहीं है का न्यूनतम अवयव 1 है।इस अवयव (अर्थात् 1) को उन सभी बिना ढके अवयवों में से घटाने तथा रेखाओं के प्रतिच्छेदन वाले अवयव में जोड़ने पर सारणी 5 प्राप्त होती है।अब स्टेप III के अनुसार शून्य निर्दिष्टीकरण कीजिए।
सारणी 5

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \hline m_1 & 9 & 0 & 1 & 8 & 0 \\ m_2 & \fbox{0} & 13 & 12 & 14 & 3 \\ m_3 & 0 & 11 & 8 & 6 & 3 \\ m_4 & 19 & 0 & 0 & 0 & 4 \\ m_5 & 11 & 4 & 0 & 0 & 0 \\ \hline \end{array}$
पद (step):VII.अब पुनः समस्त शून्यों को कम से कम एक बार ढकने के लिए न्यूनतम संख्या में रेखाएँ खींचते हैं।
सारणी 6

$\begin{tabular}{llllll} \quad & J_1 & \quad J_2 & \quad J_3 & \quad J_4 & \quad J_5 \end{tabular} \\ \begin{tabular}{c|ccccc|} \cline{2-6} m_1 & 9 \cdots & 0 \cdots & 1 \cdots & 8 \cdots & 0 \\ & \vdots & & & & \\ m_2 & \fbox{0} & 13 & 12 & 14 & 3 \\ & \vdots & & & & \\ m_3 & \xcancel{0} & 11 & 8 & 6 & 3 \\ & \vdots & & & & \\ m_4 & 19 \cdots & 0 \cdots & 0 \cdots & 0 \cdots & 4 \\ & \vdots & & & & \\ m_5 & 11 \cdots & 4 \cdots & 0 \cdots & 0 \cdots & 0 \\ \cline{2-6} \end{tabular}$
मैट्रिक्स का क्रम 5×5 है परन्तु रेखाओं की संख्या 4 है इसलिए इष्टतम हल प्राप्त नहीं हो सकता
पद (step):VIII.अब उन सभी अवयवों को जो रेखाओं से ढके नहीं हैं,का न्यूनतम अवयव 3 है।इस अवयव (अर्थात् 3) को उन सभी बिना ढके अवयवों में से घटाने तथा रेखाओं के प्रतिच्छेदन वाले अवयव में जोड़ने पर सारणी 7 प्राप्त होती है।
सारणी 7

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 12 & 0 & 1 & 8 & 0 \\ m_2 & 0 & 10 & 9 & 11 & 0 \\ m_3 & 0 & 8 & 5 & 3 & 0 \\ m_4 & 22 & 0 & 0 & 0 & 4 \\ m_5 & 14 & 4 & 0 & 0 & 0 \\ \cline{2-6} \end{array}$
पद (step):IX.सारणी 7 में शून्य निर्दिष्टीकरण निम्न चार प्रकार से कर सकते हैं (trial and error विधि से)।इसलिए इस समस्या के निम्न चार इष्टतम नियतन होंगे:
सारणी 8

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 12 & \fbox{0} & 1 & 8 & 8 \\ m_2 & \fbox{0} & 10 & 9 & 11 & 8 \\ m_3 & 2 & 8 & 5 & 3 & \fbox{0} \\ m_4 & 22 & 0 & \fbox{0} & 8 & 4 \\ m_5 &14 & 4 & 8 & \fbox{0} & 2 \\ \cline{2-6} \end{array}$
सारणी 9

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 12 & \fbox{0} & 1 & 8 & 0 \\ m_2 & \fbox{0} & 10 & 9 & 11 & 0 \\ m_3 & 0 & 8 & 5 & 3 & \fbox{0} \\ m_4 & 22 & 0 & 0 & \fbox{0} & 4 \\ m_5 &14 & 4 & \fbox{0} & 0 & 0 \\ \cline{2-6} \end{array}$
सारणी 10

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 12 & \fbox{0} & 1 & 8 & 0 \\ m_2 & 0 & 10 & 9 & 11 & \fbox{0} \\ m_3 & \fbox{0} & 8 & 5 & 3 & 0 \\ m_4 & 22 & 0 & \fbox{0} & 0 & 4 \\ m_5 &14 & 4 & 0 & \fbox{0} & 0 \\ \cline{2-6} \end{array}$
सारणी 11

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \cline{2-6} m_1 & 12 & \fbox{0} & 1 & 8 & 0 \\ m_2 & 0 & 10 & 9 & 11 & \fbox{0} \\ m_3 & \fbox{0} & 8 & 5 & 3 & 0 \\ m_4 & 22 & 0 & 0 & \fbox{0} & 4 \\ m_5 &14 & 4 & \fbox{0} & 0 & 0 \\ \cline{2-6} \end{array}$
अतः सारणी 8,9,10 और 11 से निम्न इष्टतम हल प्राप्त होते हैं:

(i) $m_1 \rightarrow J_2, m_2 \rightarrow J_1, m_3 \rightarrow J_5, m_4 \rightarrow J_3, m_5 \rightarrow J_4$
(ii) $m_1 \rightarrow J_2, m_2 \rightarrow J_1, m_3 \rightarrow J_5, m_4 \rightarrow J_4, m_5 \rightarrow J_3$
(iii) $m_1 \rightarrow J_2, m_2 \rightarrow J_5, m_3 \rightarrow J_1, m_4 \rightarrow J_3, m_5 \rightarrow J_4$
(iv) $m_1 \rightarrow J_2, m_2 \rightarrow J_5, m_3 \rightarrow J_1, m_4 \rightarrow J_4, m_5 \rightarrow J_3$
कुल समय=3+1+4+0+6=14

Assignment Problems in Optimization

Illustration:7.एक कम्पनी के पास 5 कार्य हैं एवं 5 मशीनें हैं।सम्बन्धित लागत मैट्रिक्स निम्न प्रकार है:
(A company has 5 jobs and 5 machines.The relevant matrix is given below):
$\begin{array}{|c|ccccc|} \hline & \multicolumn{5}{|c|}{\text{कार्य (Jobs)}} \\ \text{मशीन(Machines)} \downarrow & J_1 & J_2 & J_3 & J_4 & J_5 \\ \hline M_1 & 10 & 4 & 5 & 3 & 1 \\ M_2 & 13 & 11 & 9 & 12 & 10 \\ M_3 & 12 & 3 & 10 & 1 & 9 \\ M_4 & 9 & 1 & 11 & 4 & 8 \\ M_5 & 8 & 6 & 7 & 3 & 10 \\ \hline \end{array}$
समस्या को न्यूनतम लागत के लिए हल कीजिए।
(Solve the problem for least cost.)
Solution:पद (step):I.प्रत्येक पंक्ति के न्यूनतम अवयव को उसी पंक्ति के प्रत्येक अवयव में से घटाने पर पंक्ति समानयन निम्न मैट्रिक्स प्राप्त होती है:
सारणी 1

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5 \\ \cline{2-6} M_1 & 9 & 3 & 4 & 2 & 0 \\ M_2 & 4 & 2 & 0 & 3 & 1 \\ M_3 & 11 & 2 & 9 & 0 & 8 \\ M_4 & 8 & 0 & 10 & 3 & 7 \\ M_5 & 5 & 3 & 4 & 0 & 7 \\ \cline{2-6} \end{array}$
पद (step):II.सारणी के प्रत्येक स्तम्भ के न्यूनतम अवयव को उसी स्तम्भ के प्रत्येक अवयव में से घटाने पर स्तम्भ समानयन निम्न मैट्रिक्स प्राप्त होती है:
सारणी 2

$\begin{array}{cccccc} & J_1 & J_2 & J_3 & J_4 & J_5\\ \cline{2-6} M_1 & 5 & 3 & 4 & 2 & 0 \\ M_2 & 0 & 2 & 0 & 3 & 1 \\ M_3 & 7 & 2 & 9 & 0 & 8 \\ M_4 & 4 & 0 & 10 & 3 & 7 \\ M_5 & 1 & 3 & 4 & 0 & 7 \\ \cline{2-6} \end{array}$
पद (step):III.शून्य नियतन (निर्दिष्टीकरण) प्रथम पंक्ति से अवलोकन प्रारम्भ करते हुए उन पंक्तियों को चुनते हैं जिनमें एक और केवल एक शून्य हो।यहाँ पहली,तीसरी तथा चौथी तीन पंक्तियाँ ऐसी है कि प्रत्येक में एक शून्य है।इन पंक्तियों की शून्यों को वर्ग $(\square)$ से अंकित करते हैं तथा इन शून्यों से गुजरने वाले स्तम्भ की अन्य सभी शून्यों को काट (×) देते हैं।पुनः प्रथम स्तम्भ से अवलोकन प्रारम्भ करते हुए उन स्तम्भों को चुनते हैं जिनमें अचिन्हित न तो अंकित हैं और न कटी (×) है,एक और केवल एक शून्य स्तम्भों को चुनते हैं।इन स्तम्भों की शून्य को वर्ग $(\square)$ से अंकित करते हैं और इन शून्यों से गुजरने वाली पंक्ति की अन्य शून्य को काट (×) देते हैं।यहाँ ऐसा स्तम्भ प्रथम है।इस प्रकार सारणी 3 में यह नियतन निम्नानुसार है:
सारणी 3

$\begin{array}{cccccc} \quad \quad & J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \hline M_1 & 5 & 3 & 4 & 2 & \fbox{0} \\ M_2 & \fbox{0} & 2 & \xcancel{0} & 3 & 1 \\ M_3 & 7 & 2 & 9 & \fbox{0} & 8 \\ M_4 & 4 & \fbox{0} & 10 & 3 & 7 \\ M_5 & 1 & 3 & 4 & \xcancel{0} & 7 \\ \hline \end{array}$
पद (step):IV.अब समस्त शून्यों को कम से कम एक बार रेखाओं से ढकने के लिए न्यूनतम संख्या में रेखाएँ खींचते हैं जिसकी विधि निम्न प्रकार है:
सारणी 4

$\begin{array}{lllllll} & & & & \quad (2) & & \\ \quad & J_1 & \quad J_2 & \quad J_3 & \quad J_4 & \quad J_5 & \end{array} \\ \begin{array}{|c|ccccc|c} \hline M_1 & 5 \cdots & 3 \cdots & 4 \cdots & 2 \cdots & \fbox{0} & \\ & & & & & \vdots\\ M_2 & \fbox{0} \cdots & 2 \cdots & \xcancel{0} \cdots & 3 \cdots & 1 \cdots & \\ & & & & & \vdots & \\ M_3 & 7 & 2 & 9 & \fbox{0} & 8 & (3)\\ & & & & & \vdots & \\ M_4 & 4 \cdots & \fbox{0} \cdots & 10 \cdots & 3 \cdots & 7 \cdots & \\ & & & & & \vdots & \\ M_5 & 1 & 3 & 4 & \xcancel{0} & 7 & (1) \\ \hline \end{array}$
(i)सारणी 3 को पुनः बनाइये।
(ii)पंक्ति 5 को चिन्हित $(\checkmark)$ कीजिए क्योंकि इसमें नियतन नहीं है।
(iii)पंक्ति 5 के स्तम्भ 4 में शून्य हैं इसलिए स्तम्भ 4 को चिन्हित $(\checkmark)$ कीजिए।
(iv)चिन्हित $(\checkmark)$ स्तम्भ 4 की पंक्ति 3 में वर्ग $(\square)$ अंकित है,को चिन्हित $(\checkmark)$ कीजिए।
पद (step):V.अब हम सभी चिन्हित स्तम्भों से रेखाएँ खींचते हैं।फिर अचिन्हित पंक्तियों 1,2 तथा 4 जिनमें शून्य है परन्तु उनसे कोई रेखा नहीं गुजरती पर रेखा खींचते हैं।अब क्योंकि कोई ऐसी शून्य शेष नहीं है जिस पर रेखा नहीं गुजरती।
मैट्रिक्स का क्रम 5×5 है परन्तु रेखाओं की संख्या 4 है इसलिए इससे इष्टतम हल प्राप्त नहीं हो सकता।
पद (step):VI.अब उन सभी अवयवों जो रेखाओं से ढके नहीं है का न्यूनतम अवयव 1 है।इस अवयव (अर्थात् 1) को उन सभी बिना ढके अवयवों में से घटाने तथा रेखाओं के प्रतिच्छेदन वाले अवयव में जोड़ने पर सारणी 5 प्राप्त होती है।अब स्टेप III के अनुसार शून्य निर्दिष्टीकरण कीजिए।
सारणी 5

$\begin{array}{cccccc} & \quad \quad J_1 & J_2 & J_3 & J_4 & J_5 \end{array} \\ \begin{array}{c|ccccc|} \hline M_1 & 5 & 3 & 4 & 3 & \fbox{0} \\ M_2 & \xcancel{0} & 2 & \fbox{0} & 4 & 1 \\ M_3 & 6 & 1 & 8 & \fbox{0} & 8 \\ M_4 & 4 & \fbox{0} & 10 & 4 & 7 \\ M_5 & \fbox{0} & 2 & 3 & \xcancel{0} & 6 \\ \hline \end{array}$
सारणी 5 में प्रत्येक पंक्ति तथा प्रत्येक स्तम्भ में एक नियतन है इसलिए इससे निम्न प्रकार इष्टतम हल प्राप्त होता है।

$M_1 \rightarrow J_5, M_2 \rightarrow J_3, M_3 \rightarrow J_4, M_4 \rightarrow J_2, M_5 \rightarrow J_1$
न्यूनतम लागत (Min. Cost)=1+9+1+1+8=20
Illustration:8.पाँच मशीनों पर पाँच कार्य (प्रत्येक को एक-एक कार्य) निर्दिष्ट करने हैं जिनकी सम्बद्ध लागत मैट्रिक्स निम्न है।न्यूनतम निर्दिष्टीकरण समस्या को हल कीजिए:
(There are five machines and the associated cost matrix is as follows. Solve the following assignment problem):
$\begin{array}{|c|ccccc|} \hline & \multicolumn{5}{|c|}{\text{कार्य (Jobs)}} \\ \text{मशीन(Machines)} \downarrow & I & II & III & IV & V \\ \hline A & 11 & 17 & 8 & 16 & 20 \\ B & 9 & 7 & 12 & 6 & 15 \\ C & 13 & 16 & 15 & 12 & 16 \\ D & 21 & 24 & 17 & 28 & 26 \\ E & 14 & 10 & 12 & 11 & 15 \\ \hline \end{array}$
Solution:पद (step):I.प्रत्येक पंक्ति के न्यूनतम अवयव को उसी पंक्ति के प्रत्येक अवयव में से घटाने पर पंक्ति समानयन निम्न मैट्रिक्स प्राप्त होती है:
सारणी 1

$\begin{array}{c|ccccc|} & I & II & III & IV & V \\ \cline{2-6} A & 3 & 9 & 0 & 8 & 12 \\ B & 3 & 1 & 6 & 0 & 9 \\ C & 1 & 4 & 3 & 0 & 4 \\ D & 4 & 7 & 0 & 11 & 9 \\ E & 4 & 0 & 2 & 1 & 5 \\ \cline{2-6} \end{array}$
पद (step):II.सारणी के प्रत्येक स्तम्भ के न्यूनतम अवयव को उसी स्तम्भ के प्रत्येक अवयव में से घटाने पर स्तम्भ समानयन निम्न मैट्रिक्स प्राप्त होती है:
सारणी 2

$\begin{array}{c|ccccc|} & I & II & III & IV & V \\ \cline{2-6} A & 2 & 9 & 0 & 8 & 8 \\ B & 2 & 1 & 6 & 0 & 5 \\ C & 0 & 4 & 3 & 0 & 0 \\ D & 3 & 7 & 0 & 11 & 5 \\ E & 3 & 0 & 2 & 1 & 1 \\ \cline{2-6} \end{array}$
पद (step):III.शून्य नियतन (निर्दिष्टीकरण) प्रथम पंक्ति से अवलोकन प्रारम्भ करते हुए उन पंक्तियों को चुनते हैं जिनमें एक और केवल एक शून्य हो।यहाँ पहली,दूसरी तथा पाँचवीं पंक्तियाँ ऐसी है कि प्रत्येक में केवल एक शून्य है।इन पंक्तियों के शून्यों को वर्ग $(\square)$ से अंकित करते हैं तथा इन शून्यों से गुजरने वाले स्तम्भ की अन्य सभी शून्यों को काट (×) देते हैं।पुनः प्रथम स्तम्भ से अवलोकन प्रारम्भ करते हुए उन स्तम्भों को चुनते हैं जिनमें अचिन्हित न तो अंकित है और न कटी (×) है,एक और केवल एक शून्य वाले स्तम्भों को चुनते हैं। इन स्तम्भों की शून्य को वर्ग $(\square)$ से अंकित करते हैं और इन शून्यों से गुजरने वाली पंक्ति की अन्य शून्यों को काट (×) देते हैं।यहाँ ऐसा स्तम्भ प्रथम है।इस प्रकार सारणी में यह नियतन निम्नानुसार है:
सारणी 3

$\begin{array}{c|ccccc|} & I & II & III & IV & V \\ \hline A & 2 & 9 & \fbox{0} & 8 & 8 \\ B & 2 & 1 & 6 & \fbox{0} & 5 \\ C & \fbox{0} & 4 & 3 & \xcancel{0} & \xcancel{0} \\ D & 3 & 7 & \xcancel{0} & 11 & 5 \\ E & 3 & \fbox{0} & 2 & 1 & 1 \\ \hline \end{array}$
पद (step):IV.अब समस्त शून्यों को कम से कम एक बार रेखाओं से ढकने के लिए न्यूनतम संख्या में रेखाएँ खींचते हैं जिसकी विधि निम्न प्रकार है:
सारणी 4

$\begin{array}{c|ccccc|c} & I & II & III & IV & V & \\ \hline A & 2 & 9 & \fbox{0} & 8 & 8 & (3) \\ & & & \vdots & & & \\ B & 2 \cdots & 1 \cdots & 6 \cdots & \fbox{0} \cdots & 5 \cdots & \\ & & & \vdots & & & \\ C & \fbox{0} \cdots & 4 \cdots & 3 \cdots & \xcancel{0} \cdots & \xcancel{0} \cdots & \\ & & & \vdots & & & \\ D & 3 & 7 & \xcancel{0} & 11 & 5 & (1)\\ & & & \vdots & & & \\ E & 3 \cdots & \fbox{0} \cdots & 2 \cdots & 1 \cdots & 1 \cdots & \\ \hline \end{array}$
(i)सारणी 3 को पुनः बनाइये।
(ii)पंक्ति 4 को चिन्हित $(\checkmark)$ कीजिए क्योंकि इसमें नियतन नहीं है।
(iii)पंक्ति 4 के स्तम्भ 3 में शून्य हैं इसलिए स्तम्भ 3 को चिन्हित $(\checkmark)$ कीजिए।
(iv)चिन्हित $(\checkmark)$ स्तम्भ 3 की पंक्ति 1 में वर्ग $(\square)$ अंकित है,को चिन्हित $(\checkmark)$ कीजिए।
पद (step):V.अब हम सभी चिन्हित स्तम्भों से रेखाएँ खींचते हैं।फिर अचिन्हित पंक्ति 2,3 तथा 5 जिनमें शून्य हैं परन्तु उनसे कोई रेखा नहीं गुजरती,पर रेखा खींचते हैं।अब क्योंकि कोई भी शून्य शेष नहीं है जिस पर रेखा नहीं गुजरती।
मैट्रिक्स का क्रम 5×5 है परन्तु रेखाओं की संख्या 4 है इसलिए इससे इष्टतम हल प्राप्त नहीं हो सकता।
पद (step):VI.अब उन सभी अवयवों जो रेखाओं से ढके नहीं है का न्यूनतम अवयव 2 है।इस अवयव (अर्थात् 2) को उन सभी बिना ढके अवयवों में से घटाने तथा रेखाओं के प्रतिच्छेदन वाले अवयव में जोड़ने पर सारणी 5 प्राप्त होती है।अब स्टेप III के अनुसार शून्य निर्दिष्टीकरण कीजिए।
सारणी 5

$\begin{array}{c|ccccc|} & I & II & III & IV & V \\ \hline A & \fbox{0} & 7 & \xcancel{0} & 6 & 6 \\ B & 2 & 1 & 6 & \fbox{0} & 5 \\ C & \xcancel{0} & 4 & 5 & \xcancel{0} & \fbox{0} \\ D & 1 & 5 & \fbox{0} & 9 & 3 \\ E & 3 & \fbox{0} & 4 & 1 & 1 \\ \hline \end{array}$
सारणी 5 में प्रत्येक पंक्ति तथा प्रत्येक स्तम्भ में नियतन है।अर्थात् पूर्ण शून्य निर्दिष्टीकरण निम्न अनुसार प्राप्त होता है।

$A \to I, B \to IV, C \to V , D \to III, E \to II$
प्रमेय अनुसार यह नियतन मूल मैट्रिक्स का इष्टतम हल होगा।अतः समस्या का इष्टतम हल निम्न प्रकार है:
$\begin{array}{ll} \text{इष्टतम नियतन} & \text{न्यूनतम} \\ A-I & 11 \\ B-I V & 6 \\ C-V & 16 \\ D-III & 17 \\ E-II & 10 \\ \hline \text { Total } & 60 \end{array}$
उपर्युक्त उदाहरणों के द्वारा इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems) को समझ सकते हैं।

3.इष्टतमीकरण में नियतन समस्याएं पर आधारित सवाल (Questions Based on Assignment Problems in Optimization):

Assignment Problems in Optimization

(1.)निम्न नियतन समस्या को हल कीजिए:
(Solve the following assignment problem):

$\begin{array}{|c|c|c|c|c|} \hline \overset{\text{Man} \to }{\text{Job} \downarrow} & A & B & C & D \\ \hline I & 10 & 12 & 19 & 11 \\ \hline II & 5 & 10 & 7 & 8 \\ \hline III & 12 & 14 & 13 & 11 \\ \hline IV & 8 & 15 & 11 & 9 \\ \hline \end{array}$
(2.)न्यूनतम नियतन समस्या को हल करो जिसकी प्रभाविता आव्यूह (मैट्रिक्स) है:
(Solve the minimal assignment problem whose effectiveness matrix is):

$\begin{array}{l|l|l|l|l|} \cline{2-5} & I & II & III & IV \\ \cline{2-5} A & 2 & 3 & 4 & 5 \\ \cline{2-5} B & 4 & 5 & 6 & 7 \\ \cline{2-5} C & 7 & 8 & 9 & 8 \\ \cline{2-5} D & 3 & 5 & 8 & 4 \\ \cline{2-5} \end{array}$
उत्तर (Answers):(1.) $I \rightarrow B, II \rightarrow c, III \rightarrow D, IV \rightarrow A$
न्यूनतम लागत=12+7+11+8=38
(2) (i) $A \rightarrow I, B \rightarrow II, C \rightarrow III, D \rightarrow IV$
(ii) $A \rightarrow II, B \rightarrow I, C \rightarrow III, D \rightarrow IV$
न्यूनतम लागत प्रथम स्थिति=2+5+9+4=20,
न्यूनतम लागत द्वितीय स्थिति=3+4+9+4=20
उपर्युक्त सवालों को हल करने पर इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems) को ठीक से समझ सकते हैं।

Also Read This Article:- Theory of Simplex Method in LPP

4.इष्टतमीकरण में नियतन समस्याएं (Frequently Asked Questions Related to Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.निर्दिष्ट कलन विधि के मुख्य पद लिखिए। (Write Down the Main Steps of a Assignment Algorithm):

उत्तर:(I.)सर्वप्रथम लागत मैट्रिक्स की प्रत्येक पंक्ति के न्यूनतम अवयव को उसके संगत पंक्ति के प्रत्येक अवयव में से घटाकर पंक्ति समानीत (संकुचित) मैट्रिक्स (row reduced matrix) प्राप्त कीजिए।
(II.)पंक्ति समानीत (संकुचित) मैट्रिक्स के प्रत्येक स्तम्भ के न्यूनतम अवयव को उसके संगत स्तम्भ के प्रत्येक अवयव में से घटाकर दूसरी स्तम्भ समानीत (संकुचित) मैट्रिक्स (column reduced matrix) प्राप्त कीजिए।
(III.)शून्य नियतन (या निर्दिष्टीकरण)

प्रश्न:2.शून्य निर्दिष्टीकरण से आपका क्या आशय है? (What Do You Mean by Zero Assignment?):

उत्तर:(a)पद (step II) से प्राप्त मैट्रिक्स की प्रथम पंक्ति से प्रारम्भ करते हुए इनका अवलोकन इस प्रकार करिए कि उन पंक्तियों को चुनिये जिनमें एक और केवल एक शून्य है।इस शून्य को एक वर्ग $(\square)$ से अंकित करिए चूँकि एक नियतन उस अवयव पर करना है।इसके पश्चात इस अंकित शून्य के स्तम्भ में यदि कोई और शून्य हो तो उस शून्य को काट (×) दीजिए।जिससे उन्हें अन्य प्रकार से नियतन नहीं किया जाए।
(b)पुनः प्रथम स्तम्भ से प्रारम्भ करते हुए इनका अवलोकन इस प्रकार करिए कि उन स्तम्भों को चुनिये जिनमें एक और केवल एक अचिन्हित (unmarked) शून्य है।इस शून्य को एक वर्ग $(\square)$ से अंकित करिए चूँकि एक नियतन इस अवयव पर करना है अब इस शून्य की पंक्ति में यदि कोई और शून्य हो तो उस शून्य को काट (×) दीजिए जिससे उन्हें अन्य प्रकार से नियतन नहीं किया जाए।
(c)उपर्युक्त (a) तथा (b) प्रक्रिया की पुनरावृत्ति तब तक करते रहिए जब तक कि निम्न दो स्थितियों में से एक स्थिति प्राप्त न हो जाए।
(i)मैट्रिक्स की शून्य अवयव या तो वर्ग $(\square)$ से अंकित हो या काट (×) दिया जाए।
या (ii)प्रत्येक पंक्ति या स्तम्भ में शेष अचिन्हित कम से कम दो शून्य हों।
अब (i)स्थिति में अधिकतम नियतन हो गया है और स्थिति (ii) में कुछ और शून्यों का नियतन trial and error विधि से करते हैं जो इस प्रकार है।स्वेच्छा से एक अचिन्हित शून्य को वर्ग $(\square)$ से अंकित करिए और इस शून्य वाली पंक्ति तथा स्तम्भ में शेष शून्यों को काट (×) दीजिए।इस विधि की पुनरावृत्ति तब तक करिए जब तक कि मैट्रिक्स में कोई भी अचिन्हित शून्य नहीं रहे।

प्रश्न:3.नियतन समस्या का गणितीय गठन लिखिए। (Write Mathematical Formulation of Assignment Problem):

उत्तर:यदि (if) $x_{ij}=X_{i j}, Z=\underset{i=1}{\overset{n}{\sum}} \underset{j=1}{\overset{n}{\sum}} c_{i j}, x_{i j}$ को प्रत्येक $x_{i j}$ के लिए न्यूनतम (minimize) करता है,तथा साथ ही $\underset{i=1}{\overset{n}{\sum}} x_{ij}=1=\underset{j=1}{\overset{n}{\sum}} x_{ij}$ तथा $x_{i j} \geq 0$
तब $x_{ij}=X_{i j} , Z^{\prime}=\underset{i=1}{\overset{n}{\sum}} \underset{j=1}{\overset{n}{\sum}} c^{\prime}_{i j}, x_{i j}$ को भी न्यूनतम करता है।
जहाँ $C^{\prime}_{i j}=c_{i j} \pm a_i \pm b_j, i, j=1,2, \ldots n$ एवं $a_{i}$ तथा $b_{j}$ अचर हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा इष्टतमीकरण में नियतन समस्याएं (Assignment Problems in Optimization),नियतन समस्याएं (Assignment Problems) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Assignment Problems in Optimization

इष्टतमीकरण में नियतन समस्याएं
(Assignment Problems in Optimization)