Areas of Similar Triangles Class 10
1.समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Areas of Similar Triangles Class 10),समरूप त्रिभुजों के क्षेत्रफल (Areas of Similar Triangles):
समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Areas of Similar Triangles Class 10) में क्षेत्रफल को वर्ग मात्रकों (Square Units) में मापा जाता है।क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होगा।यह वास्तव में सत्य है और इसे हम अगली प्रमेय में सिद्ध करेंगे।
प्रमेय (Theorem):6.6.दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
दिया है (Given): \triangle ABC \sim \triangle PQR
सिद्ध करना है (To Prove): \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(PQR)}=\left(\frac{A B}{P Q}\right)^2=\left(\frac{B C}{Q R}\right)^2=\left(\frac{C A}{R P}\right)^2
रचना (Construction): \triangle ABC तथा \triangle PQR में क्रमशः AM \perp BC एवं PN \perp QR खींचा।
उपपत्ति (Proof): \operatorname{ar}(A B C)=\frac{1}{2} B C \times A M
तथा \operatorname{ar}(P Q R)=\frac{1}{2} QR \times PN
अतः \frac{\operatorname{ar}(A B C)}{\operatorname{ar}(P Q R)}=\frac{\frac{1}{2} \times B C \times A M}{\frac{1}{2} \times Q R \times P N} \\ \Rightarrow \frac{\operatorname{ar}(A B C)}{\operatorname{ar}(P Q R)}=\frac{B C}{Q R} \times \frac{A M}{P N} \cdots(1)
अब \triangle ABM और \triangle PQN में
\angle B=\angle Q \cdot\left(\because \triangle ABC \sim \triangle PQR \text{है} \right)
और \angle M=\angle N=90^{\circ}
अतः AA समरूपता गुणधर्म से
\triangle ABM \sim \triangle PQN \\ \therefore \frac{A M}{P N}=\frac{A B}{P Q} \cdots(2)
साथ ही \triangle ABC \sim \triangle PQR(दिया है)
इसलिए \frac{A B}{P Q}=\frac{B C}{Q R}=\frac{C A}{R P} \cdots(3)
(समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
अतः \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(PQR)} =\frac{AB}{PQ} \times \frac{AM}{PN} [(1) और (3) से]
= \frac{AB}{PQ} \times \frac{AB}{P Q} [(2) से]
= \left(\frac{A B}{P Q}\right)^2 \\\Rightarrow \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(PQR)}=\left(\frac{AB}{PQ}\right)^2=\left(\frac{BC}{QR}\right)^2=\left(\frac{CA}{RP}\right)^2 [(3) के प्रयोग से]
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Criteria for Similarity of Triangles
2.समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 के साधित उदाहरण (Areas of Similar Triangles Class 10 Solved Examples):
Example:1.मान लीजिए \triangle ABC \sim \triangle DEF है और इनके क्षेत्रफल क्रमशः 64 वर्गसेमी और 121 वर्गसेमी हैं।यदि EF=15.4 cm हो तो BC ज्ञात कीजिए।
Solution:\frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DEF)} =\frac{BC^2}{EF^2} \\ \Rightarrow \frac{64}{121} =\frac{B C^2}{(15.4)^2} \\ \Rightarrow B C^2 =(15.4)^2 \times\left(\frac{64}{(121}\right) \\ \Rightarrow B C =15.4 \sqrt{\left(\frac{64}{121}\right)} \\ =15.4 \times \frac{8}{11} \\ =1.4 \times 8 \\ \Rightarrow B C =11.2 सेमी
Example:2.एक समलम्ब ABCD जिसमें है,के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।यदि AB=2CD हो तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
Solution:समलम्ब चतुर्भुज ABCD में AB \| CD तथा AB=2CD
\triangle AOB और \triangle COD में
\angle 1=\angle 2 (एकान्तर कोण)
\angle 3=\angle 4 (एकान्तर कोण)
\angle 5=\angle 6 (शीर्षाभिमुख कोण)
AAA समरूपता गुणधर्म से
\triangle AOB \sim \triangle COD \\ \frac{\operatorname{ar}(A O B)}{\operatorname{ar}(COD)} =\frac{A B^2}{C D^2} \\ \Rightarrow \frac{\operatorname{ar}(A O B)}{\operatorname{ar}(COD)} =\frac{(2 C D)^2}{C D^2} \quad[\because AB=2 CD] \\ =\frac{4 C D^2}{C D^2} \\ =\frac{4}{1}
अतः का क्षेत्रफल:का क्षेत्रफल=4:1
Example:3.आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं।यदि AD,BC पर प्रतिच्छेद करे तो दर्शाइए कि \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DBC)}=\frac{AO}{DO} है।
Solution:दिया है (Given):तथा एक ही आधार BC पर स्थित दो त्रिभुज हैं।AD,BC को O पर प्रतिच्छेद करता है।
सिद्ध करना है (To Prove): \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DBC)}=\frac{AO}{DO}
रचना (Construction):शीर्ष A से BC \perp AE तथा शीर्ष D से DF \perp BC खींचा।
उपपत्ति (Proof):समकोण \triangle AEO तथा \triangle DFO में
\angle AEO=\angle DFO=90^{\circ} (रचना से)
\angle AOE=\angle DOF (शीर्षाभिमुख कोण)
AA समरूपता गुणधर्म से
\triangle AEO \sim \triangle DFO \\ \frac{AE}{DF}=\frac{AO}{DO} \cdots(1) \\ \triangle ABC का क्षेत्रफल=\frac{1}{2} \times BC \times AE \\ \triangle DBC का क्षेत्रफल=\frac{1}{2} \times B C \times DF \\ \frac{\operatorname{ar}(A B C)}{\operatorname{ar}(D B C)}=\frac{\frac{1}{2} \times BC \times A E}{\frac{1}{2} \times B C \times D F} \\ =\frac{A E}{D F} \\ \Rightarrow \frac{\operatorname{ar}(A B C)}{\operatorname{ar}(D B C)}=\frac{D E}{D F} \cdots(2)
(1) व (2) सेः
\frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DBC)}=\frac{AO}{DO}
Example:4.यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
Solution:दिया है (Given): \triangle ABC \sim \triangle DEF और \triangle ABC का क्षेत्रफल=\triangle DEF का क्षेत्रफल
सिद्ध करना है (To Prove): \triangle ABC \cong \triangle DEF
उपपत्ति (Proof): \triangle ABC \sim \triangle DEF
अतः \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DEF)}=\left(\frac{AB}{DE}\right)^2= \left(\frac{BC}{EF} \right)^2=\left(\frac{AC}{DF}\right)^2 \cdots(1)
(समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी भुजाओं के वर्गों के अनुपात के बराबर होता है)
ar(ABC)=ar(DEF) (दिया है)…. (2)
(1) व (2) सेः
\frac{\operatorname{ar}(DEF)}{\operatorname{ar}(DEF)}=\left(\frac{AB}{DE}\right)^2=\left(\frac{B C}{E F}\right)^2=\left(\frac{A C}{D F}\right)^2 \\ \Rightarrow 1=\left(\frac{A B}{D E}\right)^2=\left(\frac{B C}{E F}\right)^2=\left(\frac{A C}{D F}\right)^2 \\ \Rightarrow AB=DE, B C=E F, A C=DF
अब \triangle ABC तथा \triangle DEF में
AB=DE (सिद्ध किया है)
BC=EF (सिद्ध किया है)
AC=DF (सिद्ध किया है)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से
\triangle ABC \cong \triangle DEF
Example:5.एक त्रिभुज ABC की भुजाओं AB,BC और CA के मध्य-बिन्दु क्रमशः D,E और F हैं।\triangle DEF और \triangle ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
Solution:दिया है (Given): \triangle ABC की भुजाओं AB,BC और CA के मध्य-बिन्दु क्रमशः D,E,F हैं जिनको मिलाने से बनता है।
अतः DF=\frac{1}{2} BC तथा DF \| BC \cdots(1) \\ DE=\frac{1}{2} AC तथा DE \| AC \cdots(2) \\ EF=\frac{1}{2} AB तथा EF \| AB \cdots(3)
चतुर्भुज BEFD में
BE=DF तथा BE \| DF [(1) से]
BD=EF तथा BD \| EF [(3) से]
अतः BEFD समान्तर चतुर्भुज है।
अतः \angle B=\angle DFE \cdots(4)
इसी प्रकार DECF व ADEF समान्तर चतुर्भुज हैंः
अतः \angle A=\angle DEF,\angle C=\angle EDF \cdots(5) \\ \triangle ABC व \triangle DEF में
\angle A=\angle DEF [(5) से]
\angle B=\angle DFE[(4) से]
\angle C=\angle EDF [(5) से]
AAA समरूपता गुणधर्म से
\triangle ABC \sim \triangle DEF \\ \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DEF)} =\left(\frac{B C}{D F}\right)^2 \\=\left(\frac{2}{1}\right)^2 [(1) से]
\Rightarrow ar(DEF):ar(ABC)=1:4
Example:6.सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
Solution:दिया है (Given): \triangle ABC \sim \triangle DEF तथा AX और DY क्रमशः भुजाओं BC और EF की माध्यिकाएँ हैं।
सिद्ध करना है (To Prove): \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DEF)}=\frac{AX^2}{DY^2}
उपपत्ति (Proof): \triangle ABC \sim \triangle DEF (दिया है)
\Rightarrow \frac{AB}{DE}=\frac{BC}{DF}=\frac{AC}{DF} \\ \Rightarrow \frac{AB}{DE}=\frac{2 BX}{2 EY}=\frac{AC}{DF} [AX तथा DY माध्यिकाएँ हैं तथा BC=2BX,EF=2EY]
\Rightarrow \frac{AB}{DE}=\frac{BX}{EY}=\frac{AC}{DF} \cdots(1) \\ \triangle ABX और \triangle DEY में
\angle B=\angle E \quad(\because \triangle ABC \sim \triangle DEF) \\ \frac{A B}{D E}=\frac{BX}{EY} (सिद्ध किया है)
SAS समरूपता गुणधर्म से
\triangle ABX \sim \triangle DEY \\ \frac{AB}{DE}=\frac{AX}{DY} \cdots(2) \\ \frac{\operatorname{ar}(ABC)}{\operatorname{ar(DEF})}=\frac{AB^2}{DE^2} \cdots(3)
(2) व (3) से
\frac{\operatorname{ar}(ABC)}{\operatorname{ar}(DEF)}=\frac{AX^2}{DY^2}
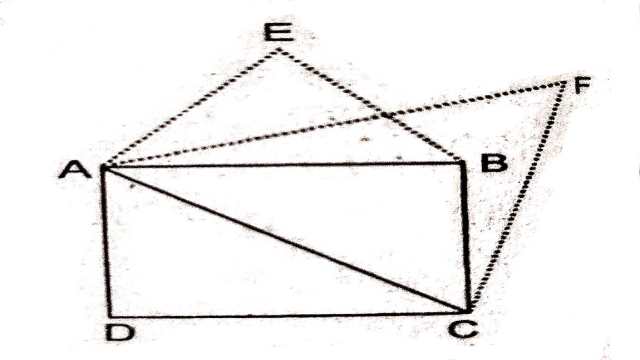
Example:7.सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
Solution:दिया है (Given):ABCD एक वर्ग है जिसकी एक भुजा AB तथा विकर्ण AC पर क्रमशः समबाहु \triangle ABE तथा \triangle ACE बनाए गए हैं।
सिद्ध करना है (To Prove): \triangle ABC का क्षेत्रफल=\frac{1}{2} \triangle ACF का क्षेत्रफल
उपपत्ति (Proof):समकोण \triangle ABC में
AC^2 =AB^2+BC^2 \\ =AB^2+AB^2(\because AB=BC) \\ =2 AB^2 \\ \Rightarrow AC=\sqrt{2} AB \cdots(1)
अब AB पर बने समबाहु \triangle ABE का क्षेत्रफल =\frac{\sqrt{3}}{4} AB^2 \cdots(2)
तथा विकर्ण AC पर बने समबाहु का क्षेत्रफल
=\frac{\sqrt{3}}{4}(AC)^2 \\ =\frac{\sqrt{3}}{4}(\sqrt{2} AB)^2 [(1) से]
=\frac{\sqrt{3}}{2}(AB)^2 \cdots(3) \\ \frac{\operatorname{ar}(ABE)}{\operatorname{ar}(ACF)}= \frac{\frac{\sqrt{3}}{4}(AB)^2}{\frac{\sqrt{3}}{2}(AB)^2} \\ =\frac{1}{2}
अतः \operatorname{ar}(ABE)=\frac{1}{2} \operatorname{ar}(ACF)
सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए
Example:8.ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है।त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात हैः
(A)2:1 (B)1:2 (C)4:1 (D)1:4
Solution:BD=\frac{1}{2} BC \\ \frac{\operatorname{ar}(ABC)}{\operatorname{ar}(BDE)} =\frac{B C^2}{B D^2} \\ \operatorname{ar(BDE)} =\frac{B C^2}{\left(\frac{1}{2} B C\right)^2} \\ =\frac{4}{1} \\ \Rightarrow \operatorname{ar}(ABC) : \operatorname{ar}(BDE)=4 : 1
सही विकल्प (C) है।
Example:9.दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं।इन त्रिभुजों के क्षेत्रफलों का अनुपात हैः
(A)2:3 (B)4:9 (C)1:16 (D)16:81
Solution:दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात=संगत भुजाओं के वर्गों का अनुपात
=(4x)^2: (9 x)^2 \\ =16 x^2 : 81 x^2 \\ =16 : 81
सही विकल्प (D) है।
उपर्युक्त उदाहरणों के द्वारा समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Areas of Similar Triangles Class 10),समरूप त्रिभुजों के क्षेत्रफल (Areas of Similar Triangles) को समझ सकते हैं।
3.समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 पर आधारित सवाल (Questions Based on Areas of Similar Triangles Class 10):
(1.)दो समरूप \triangle ABC और \triangle PQR हैं जिनके क्षेत्रफ़ल क्रमशः 100 वर्गसेमी तथा 144 वर्गसेमी है।और \triangle ABC की ऊँचाई 6 सेमी है तो \triangle PQR की ऊँचाई क्या होगी?
(2.)आकृति में AB और AC पर क्रमशः D एवं E इस प्रकार हैं कि DE \| BC एवं AD:DB=1:2 हो तो समलम्ब चतुर्भुज BDEC एवं \triangle ADE के क्षेत्रफलों में अनुपात ज्ञात कीजिए।
उत्तर (Answers):7.2 सेमी (2.)8:1
उपर्युक्त सवालों को हल करने पर समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Areas of Similar Triangles Class 10),समरूप त्रिभुजों के क्षेत्रफल (Areas of Similar Triangles) को ठीक से समझ सकते हैं।
Also Read This Article:–Similarity of Triangles Class 10
4.समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Frequently Asked Questions Related to Areas of Similar Triangles Class 10),समरूप त्रिभुजों के क्षेत्रफल (Areas of Similar Triangles) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.समरूप त्रिभुजों के क्षेत्रफलों का अनुपात किसके बराबर होता है? (The Ratio of Areas of Similar Triangles is Equal to):
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपातः
(1.)उनकी कोई भी दो संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।
(2.)उनकी संगत ऊँचाईयों के वर्गों के अनुपात के बराबर होता है।
(3.)उनकी संगत माध्यिकाओं के वर्गों के अनुपात के बराबर होता है।
(4.)उनके संगत कोणों के अर्द्धक रेखाखण्डों के वर्गों के अनुपात के बराबर होता है।
प्रश्न:2.गणितज्ञ थेल्स का समरूपता के लिए क्या योगदान है? (What is the Contribution of the Mathematician Thales to Similarity?):
उत्तर:थेल्स (लगभग 600 ईस्वी पूर्व) जिन्होंने यूनान में ज्यामिति के अध्ययन की शुरुआत की, ने समरूप त्रिभुजों से सम्बद्ध एक महत्त्वपूर्ण तथ्य, “समरूप त्रिभुजों में सदैव दो संगत भुजाओं की लम्बाईयों का अनुपात समान होता है” को सिद्ध किया था।इतिहासकारों के कथनानुसार थेल्स ने मिस्र में एक पिरैमिड की छाया की लम्बाई ज्ञात करके उस पिरैमिड की ऊँचाई ज्ञात की थी।
प्रश्न:3.समरूप त्रिभुजों के मुख्य बिन्दु लिखिए। (Write Down the HIGHLIGHTS of the Similar Triangles):
उत्तरः(1.)दो आकृतियां जिनके आकार (shape) समान हों,परन्तु आवश्यक रूप से आमाप (size) समान न हों,समरूप आकृतियां कहलाती हैं।
(2.)सभी सर्वांगसम आकृतियां समरूप होती हैं परन्तु इसका विलोम सत्य नहीं है।
(3.)भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं यदि
(i)उनके संगत कोण बराबर हों।
(ii)उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) हों।
(4.)यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए,एक रेखा खींची जाए तो ये अन्य भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
(5.)यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे तो यह रेखा तीसरी भुजा के समान्तर होती है।
(6.)यदि दो त्रिभुजों में संगत कोण बराबर हों तो उनकी संगत भुजाएँ एक ही अनुपात में होती हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (AAA समरूपता कसौटी)।
(7.)यदि दो त्रिभुजों में एक त्रिभुज के कोण क्रमशः दूसरे त्रिभुज के दो कोणों के बराबर हों तो उनके संगत कोण बराबर होते हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (AA समरूपता कसौटी)।
(8.)यदि दो त्रिभुजों में,संगत भुजाएँ एक ही अनुपात में हों तो उनके संगत कोण बराबर होते हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं (SSS समरूपता कसौटी)।
(9.)यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ एक ही अनुपात में हों तो दोनों त्रिभुज समरूप होते हैं (SAS समरूपता कसौटी)।
(10.)दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
(11.)यदि समकोण त्रिभुज के समकोण वाले शीर्ष से उसके कर्ण पर लम्ब डाला जाए तो लम्ब के दोनों ओर बनने वाले त्रिभुज सम्पूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
(12.)एक समकोण त्रिभुज में, कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
(13.)यदि एक त्रिभुज में किसी एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Areas of Similar Triangles Class 10),समरूप त्रिभुजों के क्षेत्रफल (Areas of Similar Triangles) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Areas of Similar Triangles Class 10
समरूप त्रिभुजों के क्षेत्रफल कक्षा 10
(Areas of Similar Triangles Class 10)
Areas of Similar Triangles Class 10
समरूप त्रिभुजों के क्षेत्रफल कक्षा 10 (Areas of Similar Triangles Class 10) में क्षेत्रफल को वर्ग
मात्रकों (Square Units) में मापा जाता है।क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.