Areas of Sector and Segment of Circle
1.त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Areas of Sector and Segment of Circle),त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल कक्षा 10 (Areas of Sector and Segment of a Circle Class 10):
त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Areas of Sector and Segment of Circle) में एक वृत्तीय क्षेत्र का वह भाग जो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो,उस वृत्त का एक त्रिज्यखण्ड कहलाता है तथा वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो वृत्तखण्ड कहलाता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Areas Related to Circles Class 10
2.त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल पर आधारित उदाहरण (Examples Based on Areas of Sector and Segment of Circle):
(जब तक अन्यथा न कहा जाए \pi=\frac{22}{7} का प्रयोग कीजिए।)
Example:1.6 cm त्रिज्या वाले एक वृत्त के त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है।
Solution:वृत्त की त्रिज्या (r)=6 सेमी
त्रिज्यखण्ड का कोण=60°
लघु त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{22}{7} \times \frac{6 \times 6 \times 60}{360}=\frac{132}{7} वर्ग सेमी
Example:2.एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 सेमी है।
Solution:वृत्त की परिधि 2 \pi r=22 \\ \Rightarrow 2 \times \frac{22}{7} \times r=22 \\ \Rightarrow r=\frac{22 \times 7}{2 \times 22} \\ \Rightarrow r=3.5 सेमी
वृत्त के चतुर्थांश (त्रिज्यखण्ड) का कोण \theta=90°
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{22}{7} \times \frac{35 \times 35 \times 90}{360} \\ =\frac{134.75}{14} \\ =9.625 वर्ग सेमी
Example:3.एक घड़ी की मिनट की सुई जिसकी लम्बाई 14 cm है।इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
Solution:त्रिज्यखण्ड की त्रिज्या (r)=14 cm
मिनट की सुई 1 मिनट में कोण बनाती है=6°
मिनट की सुई 5 मिनट में कोण बनाती है=6×5=30°
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{22}{7} \times \frac{14 \times 14 \times 30}{360}=\frac{154}{3} वर्गसेमी
Example:4.10 सेमी त्रिज्यावाले एक वृत्त की कोई जीवा केन्द्र पर एक समकोण अन्तरित करती है।निम्नलिखित के क्षेत्रफल ज्ञात कीजिएः
(i)संगत लघु वृत्तखण्ड (ii)संगत दीर्घ त्रिज्यखण्ड ( \pi=3.14 का प्रयोग कीजिए)।
Solution:(i)वृत्त की त्रिज्या (r)=10 सेमी
त्रिज्यखण्ड का कोण=90°
संगत लघु वृत्तखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360}-\frac{1}{2} r^2 \sin \theta \\ =\frac{3.14 \times 10 \times 10 \times 90}{360}-\frac{1}{2} \times 10 \times 10 \times \sin 90^{\circ} \\ =\frac{3.14 \times 100}{4}-50 \\ =\frac{314}{4}-50 \\ =78.5-50 \\ =28.5 वर्गसेमी
(ii)लघु त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{3.14 \times 10 \times 10 \times 90}{360}=78.5 वर्गसेमी
वृत्त का क्षेत्रफल= \pi r^{2} \\ =3.14 \times 10 \times 10 =314 वर्गसेमी
दीर्घ त्रिज्यखण्ड का क्षेत्रफल=वृत्त का क्षेत्रफल-लघु त्रिज्यखण्ड का क्षेत्रफल
=314-78.5
=235.5 वर्गसेमी
Example:5.त्रिज्या 21 cm वाले वृत्त का एक चाप केन्द्र पर 60° कोण अन्तरित करता है।ज्ञात कीजिएः
(i)चाप की लम्बाई (ii)चाप द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल (iii)संगत जीवा द्वारा बनाए गए वृत्तखण्ड का क्षेत्रफल
Solution:(i)वृत्त की त्रिज्या (r)=21 सेमी
चाप द्वारा केन्द्र पर अन्तरित कोण=60°
चाप की लम्बाई(L)= \frac{\pi r \theta}{180^{\circ}} \\ =\frac{22}{7} \times \frac{21 \times 60^{\circ}}{180^{\circ}} \\ =\frac{27720}{1260} \\ =22 सेमी
(ii)त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360^{\circ}} \\ = \frac{22}{7} \times \frac{21 \times 21 \times 60}{360} \\ = \frac{582120}{2520} \\ = 231 वर्गसेमी
(iii)वृत्तखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360^{\circ}}-\frac{1}{2} r^2 \sin \theta \\ = \frac{22}{7} \times \frac{21 \times 21 \times 66^{\circ}}{360^{\circ}}-\frac{1}{2} \times 21 \times 21 \times \sin 60^{\circ} \\ = \frac{582120}{250}-\frac{441}{2} \times \frac{\sqrt{3}}{2} \\ = \left(231-\frac{441 \sqrt{3}}{4}\right) वर्गसेमी
Example:6.15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केन्द्र पर 60° का कोण अन्तरित करती है।संगत लघु और दीर्घ वृत्तखण्डों के क्षेत्रफल ज्ञात कीजिए।(\pi=3.14 और \sqrt{3}=1.73 का प्रयोग कीजिए।)
Solution:वृत्त की त्रिज्या(r)=15 सेमी
जीवा द्वारा केन्द्र पर अन्तरित कोण=60°
लघु वृत्तखण्ड का क्षेत्रफल =\frac{\pi r^2 \theta}{360}-\frac{1}{2} r^2 \sin \theta \\ =\frac{3.14 \times 15 \times 15 \times 60}{360}-\frac{1}{2} \times 15 \times 15 \times \sin 60^{\circ} \\ =1.57 \times 5 \times 15-\frac{225}{2} \times \frac{13}{2} \\ =117.75-\frac{225}{4} \times 1.73 \\ =117.75-\frac{389.25}{4} \\ =117.75-97.3125 \\ =20.4375 वर्ग सेमी
वृत्त का क्षेत्रफल=\pi r^2 \\ =3.14 \times 15 \times 15 \\ =706.5 वर्ग सेमी
दीर्घ वृत्तखण्ड का क्षेत्रफल=706.5-20.4375
=686.0625 वर्गसेमी
Example:7.त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केन्द्र पर 120° का कोण अन्तरित करती है।संगत वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।(\pi=3.14 और \sqrt{3}=1.73 का प्रयोग कीजिए।)
Solution:वृत्त की त्रिज्या=12cm
वृत्त की जीवा का केन्द्र पर अन्तरित कोण=120°
लघु वृत्तखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360}-r^2 \sin \frac{\theta}{2} \cos \frac{\theta}{2} \\ =\frac{3.14 \times 12 \times 12 \times 120}{360}-12 \times 12 \times \sin 60^{\circ} \cos 60^{\circ} \\ =3.14 \times 48-144 \times \frac{\sqrt{3}}{2} \times \frac{1}{2} \\ =150.72-144 \times \frac{1.73}{2} \times \frac{1}{2} \\ =150.72-\frac{249.12}{4} \\ =150.72-62.28 \\ =88.44 वर्ग सेमी
Example:8.15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लम्बी रस्सी से बाँध दिया गया है (देखिए आकृति)।ज्ञात कीजिए
(i)मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii)चरे जा सकने वाले क्षेत्रफल में वृद्धि
यदि घोड़े को 5 m लम्बी रस्सी के स्थान पर 10 m लम्बी रस्सी से बाँध दिया जाए।(\pi =3.14 का प्रयोग कीजिए।)
Solution:(i)वृत्त की त्रिज्या (रस्सी की लम्बाई)=5 m
त्रिज्यखण्ड का कोण \theta=90°
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{3.14 \times 5 \times 5 \times 90}{360} \\ =\frac{7065}{360}=19.625 \mathrm{~m}^2
(ii)वृत्त की त्रिज्या (रस्सी की लम्बाई) हो=10 m
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{3.14 \times 10 \times 10 \times 90}{360} \\ =\frac{28260}{360}=78.5 \mathrm{~m}^2
क्षेत्रफल में वृद्धि=78.5-19.625
=58.875 वर्गमीटर
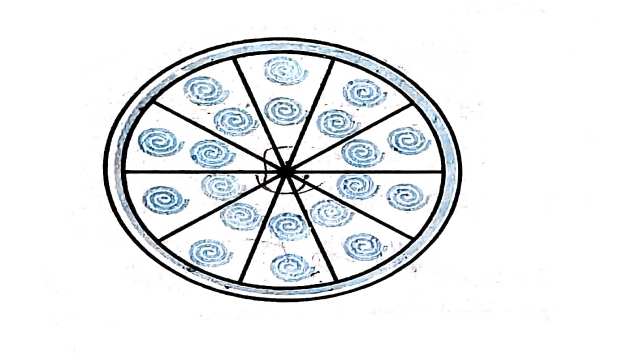
Example:9.एक वृत्ताकार ब्रूच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 35mm है।तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखण्डों में विभाजित करता है जैसा कि आकृति में दर्शाया गया है।तो ज्ञात कीजिएः
(i)कुल वांछित चाँदी के तार की लम्बाई
(ii)ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल
Solution:(i)वृत्ताकार ब्रूच की त्रिज्या=\frac{35}{2} mm
5 व्यासों की लम्बाई=35×5=175 mm
चाँदी के ब्रूच की परिधि=2 \pi r \\ =2 \times \frac{22}{7} \times \frac{35}{2}=110 \mathrm{~mm}
चाँदी के तार की कुल लम्बाई=175+110=285
(ii)वृत्ताकार ब्रूच के त्रिज्यखण्ड का कोण=\frac{360}{10}=36^{\circ}
त्रिज्यखण्ड का क्षेत्रफल =\frac{\pi r^{2} \theta}{360} \\ =\frac{22}{7} \times \frac{35}{2} \times \frac{35}{2} \times \frac{36^{\circ}}{360^{\circ}}
=96.25 वर्गमिमी
अतः ब्रूच के प्रत्येक त्रिज्यखण्ड का क्षेत्रफल= 96.25 वर्गसेमी
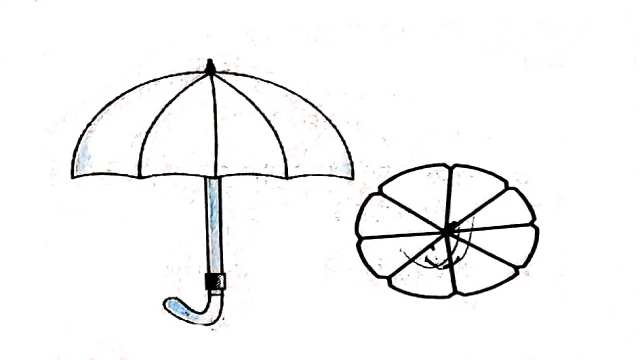
Example:10.एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं (देखिए आकृति)।छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए,इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
Solution:वृत्ताकार छतरी की त्रिज्या=45 cm
त्रिज्यखण्ड का कोण (\theta)=\frac{360^{\circ}}{8}=45^{\circ}
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360^{\circ}} \\ =\frac{22}{7} \times \frac{45 \times 45 \times 45^{\circ}}{360^{\circ}} \\ =\frac{22275}{28} वर्गसेमी
अतः दो क्रमागत तानों के बीच क्षेत्रफल=\frac{22275}{28}
Example:11.किसी कार के दो वाइपर (wipers) हैं,परस्पर कभी आच्छादित नहीं होते हैं।प्रत्येक वाइपर की पत्ती की लम्बाई 25cm है और 115° के कोण तक घूमकर सफाई कर सकता है।पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है,वह ज्ञात कीजिए।
Solution:वाइपर की पत्ती की त्रिज्या (r)=25 cm
त्रिज्यखण्ड का कोण (\theta)=115°
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{22}{7} \times \frac{25 \times 25 \times 15^6}{360} \\ =\frac{158125}{252}
दो वाइपरों के द्वारा साफ किया गया क्षेत्रफल=\frac{2 \times 158125}{252} \\ =\frac{158125}{126} वर्गसेमी
Example:12.जहाजों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए,एक लाइट हाउस (light house) 80° कोण वाले एक त्रिज्यखण्ड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है।समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाजों को चेतावनी दी जा सके।(\pi=3.14 का प्रयोग कीजिए।)
Solution:त्रिज्या (r)=16.5 km
त्रिज्यखण्ड का कोण (\theta)=80°
त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360} \\ =\frac{3.14 \times 16.5 \times 16.5 \times 80}{360} \\ =\frac{68389.2}{360}=189.57 \mathrm{~km}^2
अतः समुद्र के उस भाग का क्षेत्रफल जिसमें जहाजों को चेतावनी दी जा सके=189.97 वर्गकिलोमीटर
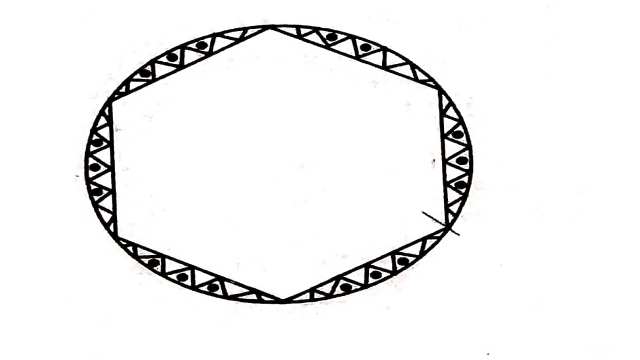
Example:13.एक गोल मेजपोश पर छः समान डिजाइन बने हुए हैं जैसा कि आकृति में दर्शाया गया है।यदि मेजपोश की त्रिज्या 28 cm है तो 0.35 रुपए प्रति सेन्टीमीटर की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए।( \sqrt{3}=1.7 का प्रयोग कीजिए)
Solution:मेजपोश पर वृत्त की त्रिज्या=28 cm
मेजपोश पर बने वृत्तखण्ड की जीवा द्वारा वृत्त के केन्द्र पर अन्तरित कोण=\frac{360^{\circ}}{6}=60°
वृत्तखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360}-\frac{r^2}{2} \sin \theta \\ =\frac{22}{7} \times \frac{28 \times 28 \times 60}{360}-\frac{28 \times 28}{2} \sin 60^{\circ} \\ =\frac{11 \times 4 \times 28}{3}-14 \times 28 \times \frac{\sqrt{3}}{2} \\ =\frac{1232}{3}-196 \times 1.7 \\ =\frac{1232}{3}-333.2 \\ =\frac{1232-999.6}{3} \\ =\frac{232.4}{3} वर्गसेमी
छः वृत्तखण्डों का क्षेत्रफल=\frac{232.4}{3} \times 6
=464.8 वर्गसेमी
डिजाइनों की बनाने की लागत=464.8×0.35
=162.68 रुपए
Example:14.निम्नलिखित में सही उत्तर चुनिएः
त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल जिसका कोण p° है,निम्नलिखित हैः
(A) \frac{p}{180^{\circ}} \times 2 \pi R
(B) \frac{P}{180^{\circ}} \times \pi R^2
(C) \frac{p}{360^{\circ}} \times 2 \pi R
(D) \frac{P}{720^{\circ}} \times 2 \pi R^2
Solution:त्रिज्यखण्ड का क्षेत्रफल=\frac{p^{\circ}}{360^{\circ}} \times \pi R^2 \\ =\frac{p^{\circ}}{720^{\circ}} \times 2 \pi R^2
अतः सही विकल्प (D) है।
उपर्युक्त उदाहरणों के द्वारा त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Areas of Sector and Segment of Circle),त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल कक्षा 10 (Areas of Sector and Segment of a Circle Class 10) को समझ सकते हैं।
3.त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल के सवाल (Areas of Sector and Segment of Circle Questions):
(1.)एक घड़ी की घण्टे की सुई 5 सेमी लम्बी है।70 मिनट में इस सुई द्वारा बनाए गए त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
(2.)10 सेमी त्रिज्या के वृत्त में एक जीवा द्वारा केन्द्र पर अन्तरित कोण 40° है, तो इस जीवा द्वारा बने लघु वृत्तखण्ड और दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।( \pi=3.14 लीजिए)
(3.)एक घड़ी की मिनट की सुई द्वारा 10 मिनट में बनाए गए त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए (\pi=\frac{22}{7} लीजिए)।
उत्तर (Answers):(1.)7.6388 वर्गसेमी (2.)1.166 सेमी,312.8834 वर्गसेमी (3.)57.75 वर्गसेमी
उपर्युक्त सवालों को हल करने पर त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Areas of Sector and Segment of Circle),त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल कक्षा 10 (Areas of Sector and Segment of a Circle Class 10) को ठीक से समझ सकते हैं।
4.वृत्त के त्रिज्यखण्ड का क्षेत्रफल (Area of a Sector of a Circle):
किसी भी वृत्त की दो त्रिज्याओं और एक चाप से घिरे हुए क्षेत्र को वृत्त का त्रिज्यखण्ड (sector) कहते हैं।
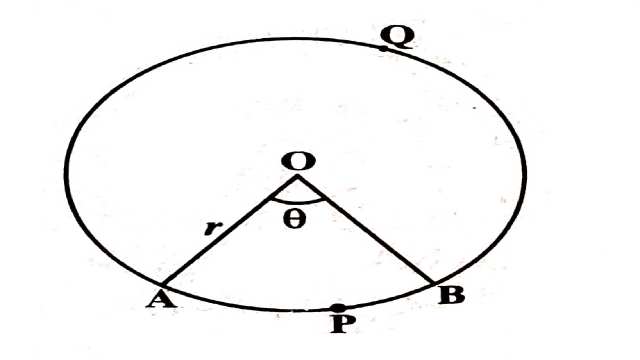
चित्र में वृत्त का एक त्रिज्यखण्ड AOB है।माना कि \angle AOB=\theta है और \theta <180°।जब कोण \theta का मान बढ़ता है तो चाप AB की लम्बाई भी उसी अनुपात में बढ़ती है।जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है तो चाप की लम्बाई=अर्द्धवृत्त के चाप की लम्बाई=\pi r
\because केन्द्र पर 180° कोण अन्तरित करने वाले चाप की लम्बाई=\pi r
\therefore केन्द्र पर \theta कोण अन्तरित करने वाले चाप की लम्बाई=\frac{\pi r \theta}{180}
इसी प्रकार जब चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है तो उसके संगत त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2}{2}
\therefore वृत्त के केन्द्र पर कोण अन्तरित करने पर बने त्रिज्यखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{2 \times 180}=\frac{\pi r^2 \theta}{360}
यदि r त्रिज्या के वृत्त के कोण \theta के त्रिज्यखण्ड के चाप की लम्बाई L और क्षेत्रफल A है तो
L=\frac{\pi r \theta}{180}=2 \pi r \times \frac{\theta}{360} \cdots(1)
और A=\frac{\pi r^2 \theta}{360}= \frac{\pi r^2 \theta}{360^{\circ}} \cdots(2)
समीकरण (1) और (2) से प्राप्त कर सकते हैंः
A=\frac{1}{2}Lr (यहाँ कोण को डिग्री में लेते हैं)
5.वृत्तखण्ड का क्षेत्रफल (Area of Segment of a Circle):
वृत्त की प्रत्येक जीवा वृत्त को दो भागों में विभाजित करती है।इससे बने प्रत्येक भाग को वृत्तखण्ड कहते हैं।छोटे भाग को लघु वृत्तखण्ड तथा बड़े भाग को दीर्घ वृत्तखण्ड कहते हैं।
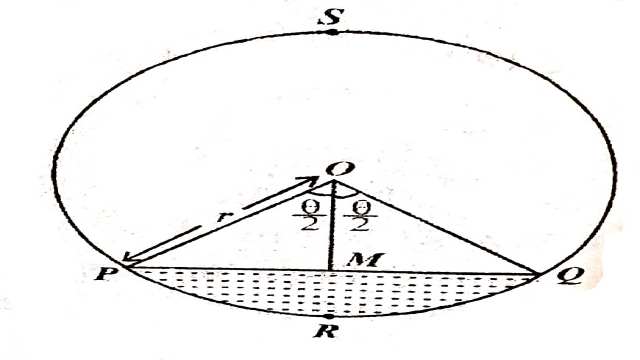
चित्र में वृत्त का केन्द्र O है और इसकी त्रिज्या r है।जीवा PQ वृत्त को दो भागों में विभाजित करती है।हमें लघु वृत्तखण्ड PRQ का क्षेत्रफल ज्ञात करना है।
माना \angle POQ=\theta \Rightarrow \angle POM=\angle QOM= \frac{\theta}{2}
त्रिज्यखण्ड OPRQ का क्षेत्रफल=लघु वृत्तखण्ड PRQ का क्षेत्रफल+ \triangle POQ का क्षेत्रफल
लघु वृत्तखण्ड PRQ का क्षेत्रफल=त्रिज्यखण्ड OPRQ का क्षेत्रफल- \triangle POQ का क्षेत्रफल
=\frac{\pi r^2 \theta}{360}-\frac{1}{2} PQ \times QM \\=\frac{\pi r^2 \theta}{360} -\frac{1}{2} \times r \sin \frac{\theta}{2} \times r \cos \frac{\theta}{2} \\ \left[\because PM=r \sin \frac{\theta}{2}, OM=r \cos \frac{\theta}{2}\right] \\ =\frac{\pi r^2 \theta}{360^{\circ}}-r^2 \sin \frac{\theta}{2} \cos \frac{\theta}{2} \\ =\frac{\pi r^2 \theta}{360^{\circ}}-\frac{r^2}{2} \sin \theta\left[\sin \theta=2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}\right]
यदि हम दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात करना चाहें तो वृत्त के क्षेत्रफल में से लघु वृत्तखण्ड का क्षेत्रफल घटाकर ज्ञात कर सकते हैं।
अतः दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल=वृत्त का क्षेत्रफल-लघु वृत्तखण्ड PRQ का क्षेत्रफल
=\pi r^2-\left[\frac{\pi r^2 \theta}{360}-\frac{r^2}{2} \sin \theta\right]
दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल=\pi r^2-\frac{r^2}{2}\left[\frac{\pi \theta}{180}-\sin \theta\right]
Also Read This Article:-Properties of Triangles Class 10
6.त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Frequently Asked Questions Related to Areas of Sector and Segment of Circle),त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल कक्षा 10 (Areas of Sector and Segment of a Circle Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिज्यखण्ड को चित्र द्वारा समझाओ। (Explain the Sector with the Help of a Diagram):

उत्तर:आकृति में छायांकित भाग OAPB केन्द्र O वाले वृत्त का एक त्रिज्यखण्ड है।इस त्रिज्यखण्ड का कोण कहलाता है।ध्यान दीजिए कि इसी आकृति में अछायांकित भाग OAQB भी वृत्त का त्रिज्यखण्ड है।स्पष्ट कारणों से OAPB एक लघु त्रिज्यखण्ड (minor sector) कहलाता है तथा OAQB एक दीर्घ त्रिज्यखण्ड (major sector) कहलाता है।इस दीर्घ त्रिज्यखण्ड का कोण 360-\angle AOB है।
प्रश्न:2.वृत्तखण्ड को चित्र द्वारा समझाओ। (Explain the Segment with the Help of a Diagram):

उत्तर:अब आकृति को देखिए,जिसमें AB केन्द्र O वाले वृत्त की एक जीवा है।अतः छायांकित भाग APB एक वृत्तखण्ड है।आप यह भी देख सकते हैं कि अछायांकित भाग AQB भी जीवा AB द्वारा निर्मित एक अन्य वृत्तखण्ड है।स्पष्ट कारणों से,APB लघु वृत्तखण्ड कहलाता है तथा AQB दीर्घ वृत्तखण्ड कहलाता है।
प्रश्न:3.त्रिज्यखण्ड और वृत्तखण्ड के सूत्र लिखिए। (Write the Formula of Sector and Segment):
उत्तर:(1.)लघु त्रिज्यखण्ड के चाप की लम्बाई (L)=\frac{\pi r \theta}{180}
(2.)लघु त्रिज्यखण्ड का क्षेत्रफल (A)=\frac{\pi r^2 \theta}{360}
(3.)लघु त्रिज्यखण्ड का क्षेत्रफल (A)=\frac{1}{2} L r
(4.)घड़ी की मिनट की सुई 1 मिनट में 6° के कोण से घूमती है।
(5.)घड़ी की घण्टे की सुई 1 मिनट में \frac{1}{2}^{\circ} के कोण से घूमती है।
(6.)लघु वृत्तखण्ड का क्षेत्रफल=\frac{\pi r^2 \theta}{360}-\frac{r^2}{2} \sin \theta
(7.)दीर्घ वृत्तखण्ड का क्षेत्रफल=\pi r^2-\frac{r^2}{2}\left(\frac{\pi \theta}{180^{\circ}}- \sin \theta \right)
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Areas of Sector and Segment of Circle),त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल कक्षा 10 (Areas of Sector and Segment of a Circle Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Areas of Sector and Segment of Circle
त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल
(Areas of Sector and Segment of Circle)
Areas of Sector and Segment of Circle

त्रिज्यखण्ड और वृत्तखण्ड के क्षेत्रफल (Areas of Sector and Segment of Circle) में एक
वृत्तीय क्षेत्र का वह भाग जो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो,उस वृत्त का
एक त्रिज्यखण्ड कहलाता है
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.