Area of Triangles and Parallelograms
1.त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Area of Triangles and Parallelograms),त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Triangles and Parallelograms Class 9):
त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Area of Triangles and Parallelograms) के इस आर्टिकल में ऐसे त्रिभुजों एवं समान्तर चतुर्भुजों के क्षेत्रफल ज्ञात करना सीखेंगे जो एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हों।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Area of Parallelograms Class 9
2.त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल के साधित उदाहरण (Area of Triangles and Parallelograms Solved Examples):
Example:1.समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं।दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD और आयत ABEF जो कि एक ही आधार AB पर स्थित हैं और ar(ABCD)=ar(ABEF)
सिद्ध करना है (To Prove):समान्तर चतुर्भुज ABCD का परिमाप>आयत ABEF का परिमाप
अर्थात्
AB+BC+CD+DA>AB+BE+EF+AF
उपपत्ति (Proof): \triangle AFD में, \angle A=90^{\circ}
\therefore DA>FA …. (1)
और \triangle BCE में \angle CEB=90^{\circ}
BC>BE ….. (2)
तथा AB=EF (आयत की सम्मुख भुजाएँ)
CD=AB (समान्तर चतुर्भुज की सम्मुख भुजाएँ)… (4)
(1),(2),(3) और (4) सेः
DA+BC+AB+CD>FA+BE+EF+FA
\Rightarrow AB+BC+CD+DA>AB+BE+EF+FA
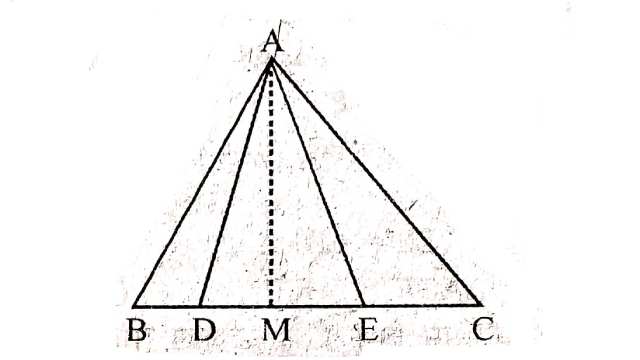
Example:2.आकृति में भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं कि BD=DE=EC है।दर्शाइए कि ar(ABD)=ar(ADE)=ar(AEC) है।
क्या आप उस प्रश्न का उत्तर दे सकते हैं जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है”?
[टिप्पणी:ध्यान दीजिए कि BD=DE=EC लेने से \triangle ABC तीन त्रिभुजों ABD,ADE और AEC में विभाजित हो जाता है जिनके क्षेत्रफल बराबर हैं।इसी प्रकार,BC को n बराबर भागों में विभाजित करके और इस भुजा को विभाजित करने वाले बिन्दुओं को सम्मुख शीर्ष A से मिलाकर आप इस त्रिभुज को बराबर क्षेत्रफलों वाले n त्रिभुजों में विभाजित कर सकते हैं।
Solution:दिया है (Given):में, D और E भुजा BC पर दो बिन्दु इस प्रकार हैं कि BD=DE=EC
सिद्ध करना है (To Prove):ar(ABD)=ar(ADC)=ar(AEC)
रचना (Construction): AM \perp BC खींचा।
उपपत्ति (Proof): \operatorname{ar}(ABD)=\frac{1}{2} \times BD \times AM \\ \operatorname{ar}(ADE)=\frac{1}{2} \times DE \times AM
और \operatorname{ar}(AEC)=\frac{1}{2} \times EC \times AM
चूँकि BD=DE=EC (दिया है)
अतःar(ABD)=ar(ADC)=ar(AEC)
Example:3.आकृति में ABCD,DCFE और ABFE समान्तर चतुर्भुज है।दर्शाइए कि ar(ADE)=ar(BCF) है।
Solution:दिया है (Given):ABCD,DCFE और ABFE तीन समान्तर चतुर्भुज हैं।
सिद्ध करना है (To Prove):ar(ADE)=ar(BCF)
उपपत्ति (Proof): \triangle ADE और \triangle BCF में
AB=BF (स.च. की सम्मुख भुजाएँ)
AD=BC (स.च. की सम्मुख भुजाएँ)
DE=CF (स.च. की सम्मुख भुजाएँ)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से
\triangle ADE \cong \triangle BCF
अतः ar(ADE)=ar(BCF)
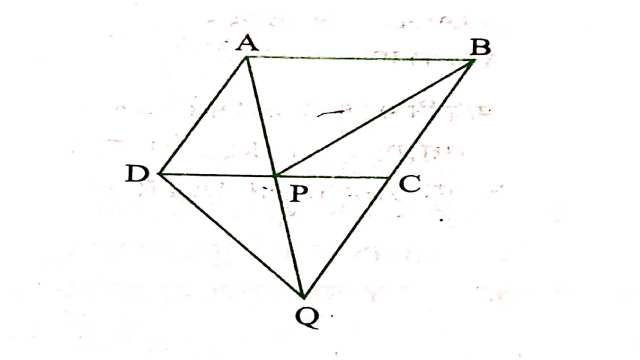
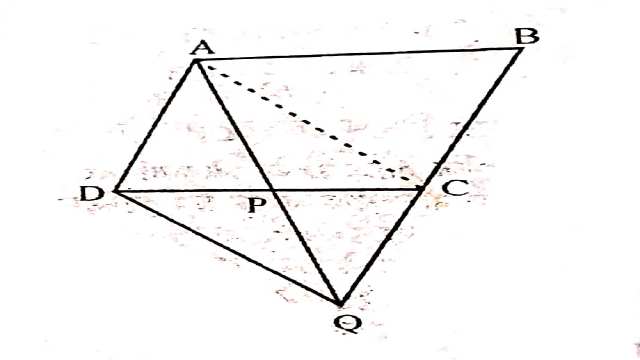
Example:4.आकृति,ABCD एक समान्तर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD=CQ है।यदि AQ भुजा DC को P पर प्रतिच्छेद करती है,तो दर्शाइए कि ar(BPC)=ar(DPQ) है।
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है।BC को Q तक बढ़ाया गया है कि AD=CQ। AQ,DC को P पर प्रतिच्छेद करता है।
सिद्ध करना है (To Prove):ar(BPC)=ar(DPQ)
रचना (Construction):A और C को मिलाया।
उपपत्ति (Proof):AD=CQ
और AD \| CQ
\therefore ADQC एक समान्तर चतुर्भुज है।
\therefore ar(DPQ)=ar(APC) … (1)
(चूँकि समान्तर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले चार त्रिभुजों में बाँटते हैं)
\triangle APC तथा \triangle BPC एक ही आधार PC तथा समान समान्तर भुजाओं AB व DC के बीच स्थित हैं अतः
ar(APC)=ar(BPC) … (2)
(1) व (2) सेः
ar(BPC)=ar(DPQ)
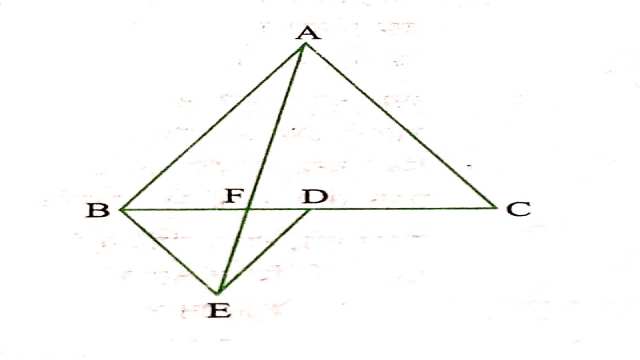
Example:5.आकृति में, ABC और BDE दो समद्विबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है।यदि AE भुजा BC को F पर प्रतिच्छेद करती है,तो दर्शाइए कि
(i) \operatorname{ar}(BDE)=\frac{1}{4} \operatorname{ar}(ABC)
(ii) \operatorname{ar}(BDE)=\frac{1}{2} \operatorname{ar}(BAE)
(iii)ar(ABC)=2ar(BEC)
(iv)ar(BFE)=ar(AFD)
(v)ar(BFE)=2ar(FED)
(vi) \operatorname{ar}(F E D)=\frac{1}{8} \operatorname{ar}(AFC)
Solution:दिया है (Given):दो समबाहु त्रिभुज \triangle ABC और \triangle BDE हैं और BC का मध्य-बिन्दु D है।AE,BC को F पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove):(i) \operatorname{ar}(BDE)=\frac{1}{4} \operatorname{ar}(ABC)
(ii) \operatorname{ar}(BDE)=\frac{1}{2} \operatorname{ar}(BAE)
(iii)ar(ABC)=2ar(BEC)
(iv)ar(BFE)=ar(AFD)
(v)ar(BFE)=2ar(FED)
(vi) \operatorname{ar}(F E D)=\frac{1}{8} \operatorname{ar}(AFC)
रचना (Construction):E और C तथा A और D को मिलाया।
उपपत्ति (Proof):(i)माना \triangle ABD की भुजा BD=x
\therefore \operatorname{ar}(BDE)=\frac{\sqrt{3}}{4} x^2
अब \triangle ABC की भुजा=2x
\operatorname{ar}(ABC) =\left(\frac{\sqrt{3}}{4}\right)(2 x)^2 \\ =\frac{\sqrt{3}}{4} \times 4x^2 \\ \therefore \operatorname{ar}(BDE) =\frac{1}{4} \operatorname{ar}(ABC)
(ii) \angle ACB=\angle EBC=60^{\circ}
परन्तु ये एकान्तर कोण हैं।
\because BE \| AC
अब \triangle BEC और \triangle BAE समान आधार BE और समान समान्तर रेखाओं AC और BE के बीच स्थित हैं।
ar(BEC)=ar(BAE) …. (1)
पुनः में D,BC का मध्य-बिन्दु है।
\therefore \operatorname{ar}(B D E)=\frac{1}{2} \operatorname{ar}(BEC) \cdots(2)
(1) और (2) सेः
\therefore \operatorname{ar}(B D E)=\frac{1}{2} \operatorname{ar}(BAE)
(iii) \triangle BCE में DE माध्यिका है।त्रिभुज की माध्यिका त्रिभुज को समान क्षेत्रफल वाले त्रिभुजों में बाँटती हैं।
\therefore ar(BDE)=ar(CDE)
ar(BEC)=2ar(BED) … (1)
परन्तु \operatorname{ar}(BDE)=\frac{1}{4} \operatorname{ar}(ABC) \cdots(2)
(1) और (2) सेः
\operatorname{ar}(BEC)=\frac{1}{2} \operatorname{ar}(ABC)
(iv) \angle BDE=\angle DBA=60^{\circ}
परन्तु ये एकान्तर कोण युग्म है।
\therefore AB \| DE
अब \triangle ADE और \triangle BED समान आधार ED पर स्थित हैं और समान समान्तर रेखाओं AB और DE के बीच स्थित है।
\therefore ar(ADE)=ar(BED)
दोनों पक्षों में ar(FED) घटाने परः
ar(ADE)-ar(FED)=ar(BED)-ar(FED)
\Rightarrow ar(AFD)=ar(BFE)
(v)ar(BFE)=ar(AFD)…..(1)
\operatorname{ar}(AFD)=\frac{1}{2} \times FD \times AD \cdots(2)
तथा \operatorname{ar}(BFE)=\frac{1}{2} \times BF \times \frac{1}{2} AD \cdots(3)
(1),(2) व (3) सेः
\frac{1}{4} B F \times AD=\frac{1}{2} FD \times AD \\ \Rightarrow BF=2 FD
(3) में रखने परः
\operatorname{ar}(BFE) =\frac{1}{2} \times 2 FD \times \frac{1}{2} AD \\ =\frac{1}{2} \times F D \times A D \cdots(4)
अब ar(FED) =\frac{1}{2} \times FD \times \frac{1}{2} AD \\ =\frac{1}{4} \times F D \times A D \cdots(5)
(4) व (5) सेः
ar(BFE)=2ar(FED)
(vi)2FD=BF
BD=x \Rightarrow B F=\frac{2}{3} x, F D=\frac{x}{3} \\ \operatorname{ar}(F E D) =\frac{1}{2} \times F D \times \frac{1}{2} A D \\=\frac{1}{2} \times \frac{x}{3} \times \frac{1}{2} A D=\frac{1}{12} A D \cdots(1) \\ \operatorname{ar}(A F C) =\frac{1}{2} \times F C \times A D \\ =\frac{1}{2} \times \frac{4x}{3} \times AD =\frac{2 x}{3} A D \\=\frac{8 x}{12} A D \cdots(2)
(1) व (2) सेः
\operatorname{ar}(FED)=\frac{1}{8} \operatorname{arc}(AFC)
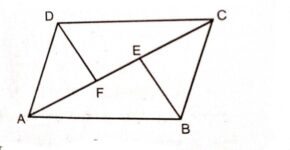
Example:6.चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं।दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है।
Solution:दिया है (Given):एक चतुर्भुज ABCD जिसमें विकर्ण AC और BD परस्पर P पर मिलते हैं।
सिद्ध करना है (To Prove):ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
उपपत्ति (Proof): \operatorname{ar}(APB)=\frac{1}{2} \times BP \times AN \cdots(1)
और \operatorname{ar}(APD)=\frac{1}{2} \times PD \times AN \cdots(2)
तथा \operatorname{ar}(C P D)=\frac{1}{2} \times PD \times CM \cdots(3)
और \operatorname{ar}(BPC)=\frac{1}{2} \times BP \times CM \cdots(4)
(1) में (2) का भाग देने परः
\frac{\operatorname{ar}(APB)}{\operatorname{ar}(APD)}=\frac{\frac{1}{2} \times RP \times AN}{\frac{1}{2} \times PD \times AN}=\frac{B P}{P D} \cdots(5)
(4) में (3) का भाग देने परः
\frac{\operatorname{ar}(B P C)}{\operatorname{ar}(C P D)}=\frac{\frac{1}{2} \times B P \times C M}{\frac{1}{2} \times P D \times C M}=\frac{B P}{P D} \cdots(6)
(5) व (6) सेः
\frac{\operatorname{ar}(APB)}{\operatorname{ar}(APD)}=\frac{\operatorname{ar}(BPC)}{\operatorname{ar(CPD)}}
ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
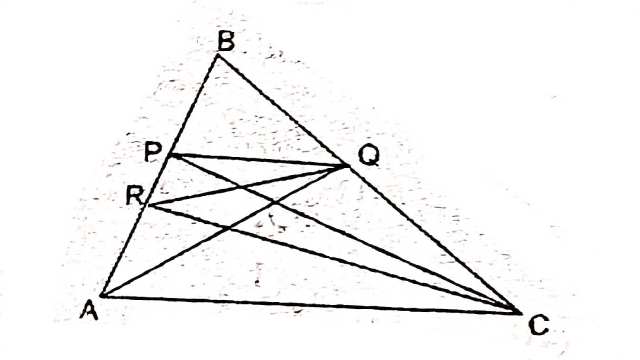
Example:7.P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु हैं तथा R रेखाखण्ड AP का मध्य-बिन्दु है।दर्शाइए कि
(i) \operatorname{ar}(PRQ)=\frac{1}{2} \operatorname{ar}(ARC)
(ii) \operatorname{ar}(RQC)=\frac{3}{8} \operatorname{ar}(ABC)
(iii) \operatorname{ar}(PBQ)=\operatorname{ar}(ARC)
Solution:दिया है (Given): \triangle ABC में भुजाओं AB और BC के मध्य-बिन्दु क्रमशः P और Q हैं।AP का मध्य-बिन्दु R है।
सिद्ध करना है (To prove):(i) \operatorname{ar}(PRQ)=\frac{1}{2} \operatorname{ar}(ARC)
(ii) \operatorname{ar}(RQC)=\frac{3}{8} \operatorname{ar}(ABC)
(iii) \operatorname{ar}(PBQ)=\operatorname{ar}(ARC)
रचना (Construction):AQ और PC को मिलाया।
उपपत्ति (Proof):(i) \operatorname{ar}(PQR)=\frac{1}{2} \operatorname{ar}(APQ)
[\because QR, \triangle APQ की माध्यिका है और यह त्रिभुज को समान क्षेत्रफल वाले त्रिभुजों में बाँटती है।]
=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(ABQ)
[\because QP,\triangle ABQ की माध्यिका है]
=\frac{1}{4} \times \frac{1}{2} \operatorname{ar}(A B C)
[\because AQ, \triangle ABC की माध्यिका है।]
\operatorname{ar}(PQR)=\frac{1}{8} \operatorname{ar}(ABC) \cdots(1)
पुनः \operatorname{ar}(A R C)=\frac{1}{2} \operatorname{ar}(A P C)
[\because CR, \triangle APC की माध्यिका है।]
=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(A B C)
[\because CP, \triangle ABC की माध्यिका है।]
\operatorname{ar}(A R C)=\frac{1}{4} \operatorname{ar}(A B C) \cdots(2)
समीकरण (1) व (2) सेः
\operatorname{ar}(PQR) =\frac{1}{8} \operatorname{ar}(A B C) \\ =\frac{1}{2} \times \frac{1}{4} \operatorname{ar}(ABQ) \\ \Rightarrow \operatorname{ar}(PQR) =\frac{1}{2} \operatorname{ar}(ARC)
(ii)ar(RQC)=ar(RQA)+ar(AQC)-ar(ARC) … (3)
अब (\triangle RQA)=\frac{1}{2} \operatorname{ar}(PQA)
[\because RQ, \triangle PQA की माध्यिका है।]
=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(AQB)
[\because PQ, \triangle AQB की माध्यिका है।]
=\frac{1}{4} \operatorname{ar}(A Q B) \\ =\frac{1}{4} \times \frac{1}{2} \operatorname{ar}(ABC)
[\because AQ, \triangle ABC की माध्यिका है।]
\operatorname{ar}(\triangle RQA)=\frac{1}{8} \operatorname{ar}(ABC) \cdots(4) \\ \operatorname{ar}(AQC)=\frac{1}{2} \operatorname{ar}(ABC) \cdots(5)
[ \because AQ, \triangle ABC की माध्यिका है।]
\operatorname{ar}(ARC)=\frac{1}{2} \operatorname{ar}(APC)
[ \because CR, \triangle APC की माध्यिका है।]
=\frac{1}{2} \times \frac{1}{2} ar(ABC)
[ \because CP, \triangle ABC की माध्यिका है।]
\operatorname{ar}(ARC)=\frac{1}{4} \operatorname{ar}(ABC) \cdots(6)
(3),(4),(5) व (6) सेः
\operatorname{ar}(RQC)=\frac{1}{8} \operatorname{ar}(A B C)+\frac{1}{2} \operatorname{ar}(A B C)-\frac{1}{4} \operatorname{ar}(A B C) \\ =\left(\frac{1}{8}+\frac{1}{2}-\frac{1}{4}\right) \operatorname{ar}(A B C) \\ \Rightarrow \operatorname{ar}(RQC)=\frac{3}{8} \operatorname{ar}(ABC)
(iii) \operatorname{ar}(PBQ)=\frac{1}{2} \operatorname{ar}(ABQ)
[PQ, \triangle ABQ की माध्यिका है।]
=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(ABC)
[\because AQ, \triangle ABC की माध्यिका है।]
\operatorname{ar}(ABQ) =\frac{1}{4} \operatorname{ar}(ABC) \\ \Rightarrow ar(PBQ)=ar(ARC) [समीकरण (6) से]
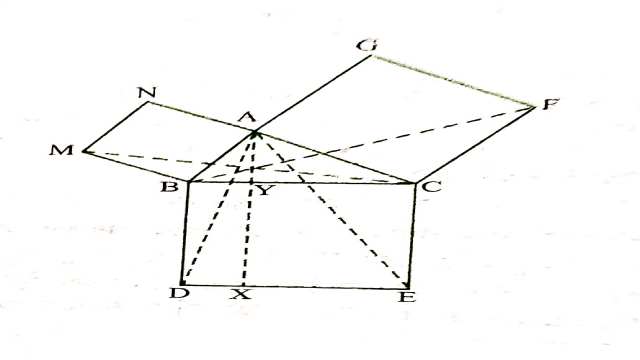
Example:8.आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है।BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं।रेखाखण्ड AX \perp DE भुजा BC को बिन्दु Y पर मिलता है।दर्शाइए किः
(i) \triangle MBC \cong \triangle(ABD)
(ii)ar(BYXD)=2ar(MBC)
(iii)ar(BYXD)=ar(ABMN)
(iv) \triangle FCB \cong \triangle ACE
(v)ar(CYXE)=2ar(FCB)
(vi)ar(CYXE)=ar(ACFG)
(vii)ar(BCED)=ar(ABMN)+ar(ACFG)
Solution:दिया है (Given): \triangle ABC में \angle A=90^{\circ} और वर्ग BCED, ACFG व ABMN क्रमशः भुजाओं BC,CA और AB पर बने हैं। AX \perp DE जो कि BC को Y पर काटती है।
सिद्ध करना है (To Prove):(i) \triangle MBC \cong \triangle(ABD)
(ii)ar(BYXD)=2ar(MBC)
(iii)ar(BYXD)=ar(ABMN)
(iv) \triangle FCB \cong \triangle ACE
(v)ar(CYXE)=2ar(FCB)
(vi)ar(CYXE)=ar(ACFG)
(vii)ar(BCED)=ar(ABMN)+ar(ACFG)
उपपत्ति (Proof):(i) \triangle MBC और \triangle ABD में
MB=AB (एक ही वर्ग की भुजाएँ)
BC=BD (एक ही वर्ग की भुजाएँ)
\angle MBC=\angle ABD [ \because \angle MBC=90^{\circ}+\angle ABC और \angle ABD=90^{\circ}+\angle ABC ]
SAS सर्वांगसमता गुणधर्म से
\triangle MBC \cong \triangle ABD
(ii)ar(MBC)=2ar(ABD) … (1)
(सर्वांगसम त्रिभुजों के क्षेत्रफल समान होते हैं)
अब आयत BYXD और \triangle ABD एक ही आधार और एक ही समान्तर रेखाओं के बीच हैं।
ar(BYXD)=2ar(ABD) … (2)
(1) व (2) सेः
ar(BYXD)=2ar(MBC) … (3)
(iii)पुनः वर्ग ABMN और \triangle MBC एक ही आधार और एक ही समान्तर रेखाओं के बीच हैं।
2ar(MBC)=2ar(ABMN) …. (4)
(3) और (4) सेः
ar(BYXD)=ar(ABMN)
(iv) \triangle FCB और \triangle ACE में
BC=CE (एक ही वर्ग की भुजाएँ)
CF=AC (एक ही वर्ग की भुजाएँ)
\angle BCF=\angle ACE \left[\because \angle BCF=\angle ACE=90^{\circ}+\angle ACB \right]
SAS सर्वांगसमता गुणधर्म सेः
\triangle FCB \cong \triangle ACE
(v)ar(FCB)=ar(ACE)…. (5)
[सर्वांगसम त्रिभुजों के क्षेत्रफल समान होते हैं।]
\triangle ACE और आयत CYXE एक ही आधार CE पर और एक ही समान्तर रेखाओं AX और CE के बीच स्थित हैं।
\therefore ar(CYXE)=2ar(ACE) … (6)
(5) व (6) सेः
ar(CYXE)=2ar(FCB) …. (7)
(vi) \triangle BCF और वर्ग ACFG एक ही आधार CF और एक ही समान्तर रेखाओं CF और BG के बीच स्थित हैं।
\therefore ar(ACFG)=2ar(BCF) … (8)
(5),(6),(7) और (8) सेः
ar(CYXE)=ar(ACFG) …..(9)
(vii)(7),(8) और (9) को जोड़ने परः
ar(BXYD)+ar(CYXE)=ar(ABMN)+ar(ACFG)
\Rightarrow ar(BCED)=ar(ABMN)+ar(ACFG)
उपर्युक्त उदाहरणों के द्वारा त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Area of Triangles and Parallelograms),त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Triangles and Parallelograms Class 9) को समझ सकते हैं।
3.त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल के सवाल (Area of Triangles and Parallelograms Questions):
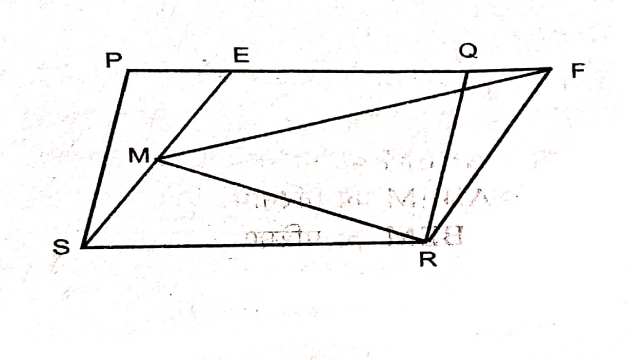
(1.)यदि चित्र मे PQRS और EFRS दो समान्तर चतुर्भुज हैं तो \operatorname{ar}(MFR)=\frac{1}{2} \operatorname{ar}(PQRS) सिद्ध करो।
(2.)यदि चित्र में PSDA एक समान्तर चतुर्भुज है।PS बिन्दु Q और R इस प्रकार लिए गए हैं कि PQ=QR=RS है तथा PA \| QB \| RC है।सिद्ध कीजिए कि ar(\triangle PQE)=ar(\triangle CFD) है।
उपर्युक्त सवालों को हल करने पर त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Area of Triangles and Parallelograms),त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Triangles and Parallelograms Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Area of Triangles Class 9
4.त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Frequently Asked Questions Related to Area of Triangles and Parallelograms),त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Triangles and Parallelograms Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 की महत्त्वपूर्ण बातें लिखिए। (Area of Triangles and Parallelograms Class 9 Write Down the Important Points):
उत्तर:(1.)एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (किसी मात्रक में) एक संख्या होती है।
(2.)दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं परन्तु इसका विलोम आवश्यक रूप से सत्य नहीं है।
(3.)यदि एक आकृति T द्वारा निर्मित कोई तलीय क्षेत्र किन्हीं दो आकृतियों P और Q द्वारा निर्मित अनातिव्यापी तलीय क्षेत्रों से मिलकर बना है तो ar(T)=ar(P)+ar(Q) है,जहाँ ar(X) आकृति X का क्षेत्रफल व्यक्त करता है।
(4.)दो आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित कही जाती है,यदि उनमें एक उभयनिष्ठ आधार (एक भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (का शीर्ष) उस आधार के समान्तर किसी रेखा पर स्थित हों।
(5.)एक ही आधार (या बराबर आधारों) वाले और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
(6.)समान्तर चतुर्भुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब का गुणनफल होता है।
(7.)एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले समान्तर चतुर्भुज एक ही समान्तर रेखाओं के बीच स्थित होते हैं।
(8.)यदि एक त्रिभुज और एक समान्तर चतुर्भुज एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हों तो त्रिभुज का क्षेत्रफल समान्तर चतुर्भुज के क्षेत्रफल का आधा होता है।
(9.)एक ही आधार (या बराबर आधारों) वाले और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
(10.)त्रिभुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब के गुणनफल का आधा होता है।
(11.)एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले दो त्रिभुज एक ही समान्तर रेखाओं के बीच स्थित होते हैं।
(12.)त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
प्रश्न:2.आयताकार प्रदेश का क्षेत्रफल अभीगृहीत क्या है? (What is Area of a Rectangular Region Axiom?):
उत्तर:यदि AB=a मी, AD=b मी तो, ar(आयताकार प्रदेश ABCD)=ab वर्गमीटर।आगे जहाँ भी बहुभुज प्रदेश के क्षेत्र का प्रयोग किया जाएगा वहाँ यही समझा जाएगा कि वह क्षेत्रफल उपर्युक्त अभीगृहीत के अनुसार है।
प्रश्न:3.समलम्ब चतुर्भुज और समान्तर चतुर्भुज किसे कहते हैं? (What are a Trapezium and a Parallelogram?):
उत्तर:उस चतुर्भुज को समलम्ब चतुर्भुज (Trapezium) कहते हैं जिसकी सम्मुख भुजाओं का एक युग्म परस्पर समान्तर हो।
उस चतुर्भुज को समान्तर चतुर्भुज (Parallelogram) कहते हैं जिसकी सम्मुख भुजाओं का प्रत्येक युग्म परस्पर समान्तर हो।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Area of Triangles and Parallelograms),त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Triangles and Parallelograms Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Area of Triangles and Parallelograms
त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल
(Area of Triangles and Parallelograms)
Area of Triangles and Parallelograms
त्रिभुजों और समान्तर चतुर्भुजों के क्षेत्रफल (Area of Triangles and Parallelograms) के
इस आर्टिकल में ऐसे त्रिभुजों एवं समान्तर चतुर्भुजों के क्षेत्रफल ज्ञात करना सीखेंगे जो
एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हों।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.