Area of Parallelograms and Triangles
1.समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Area of Parallelograms and Triangles),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms and Triangles Class 9):
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Area of Parallelograms and Triangles) के इस आर्टिकल में विभिन्न आकृतियों जैसे आयत,वर्ग,समान्तर चतुर्भुज,त्रिभुज इत्यादि आकृतियों के क्षेत्रफलों के बीच सम्बन्ध का उस प्रतिबन्ध के अन्तर्गत अध्ययन करके जब ये एक ही आधार पर स्थित हों और एक ही समान्तर रेखाओं के बीच में हों,क्षेत्रफलों को ज्ञात करने वाले सूत्रों को अधिक प्रबल बनाने का प्रयत्न किया जाएगा।यह अध्ययन त्रिभुजों की समरूपता के कुछ परिणामों को समझने में बहुत उपयोगी रहेगा।
दो आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित कही जाती हैं यदि उनका एक उभयनिष्ठ आधार (भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (या का शीर्ष) उस आधार के समान्तर किसी रेखा पर स्थित हों।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Quadrilaterals Class 9
2.समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल के उदाहरण (Area of Parallelograms and Triangles Examples):
Example:1.निम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हैं?ऐसी स्थिति में,उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
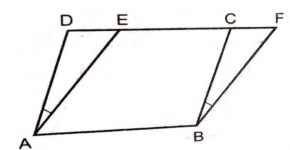
Example:1(i).
Solution: \triangle PCD और समलम्ब चतुर्भुज ABCD
उभयनिष्ठ आधार: DC
समान्तर रेखाएँ: AB \parallel DC
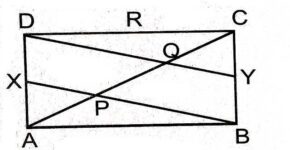
Example:1(ii).
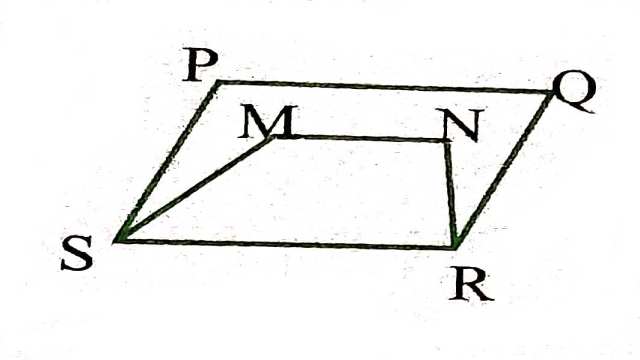
Solution:आकृतियाँ PQRS व SRNM एक ही समान्तर रेखाओं के बीच स्थित नहीं है।
Example:1(iii).
Solution: \triangle QRT और चतुर्भुज RQTS
उभयनिष्ठ आधार:QR
समान्तर रेखाएँ: PS \parallel QR
Example:1(iv).
Solution: \triangle PQR और समान्तर चतुर्भुज ABCD एक ही आधार पर स्थित नहीं है।
Example:1(v).
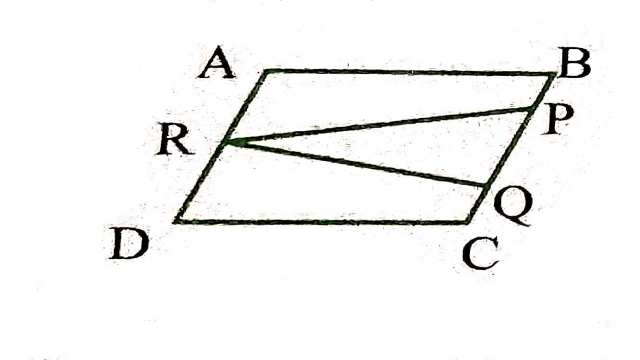
Solution:चतुर्भुज ABCD और चतुर्भुज ADQP उभयनिष्ठ आधार:AD
समान्तर रेखाएँ: AD \parallel BQ
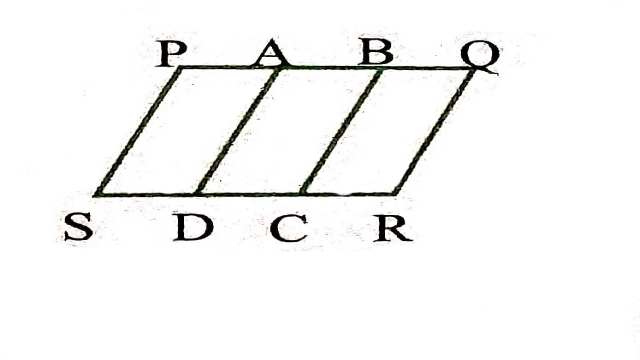
Example:1(vi).
Solution:आकृतियाँ एक ही आधार पर स्थित नहीं हैं।
उपर्युक्त उदाहरणों के द्वारा समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Area of Parallelograms and Triangle),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms and Triangle Class 9) को समझ सकते हैं।
3.समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल की समस्याएं (Area of Parallelograms and Triangles Problems):
(1.)एक ही आधार एवं एक ही समान्तर रेखा युग्म के मध्य निम्न आकृतियाँ अपनी अभ्यास पुस्तिका में बनाइए
(i)एक अधिक कोण त्रिभुज और एक समलम्ब चतुर्भुज
(ii)एक समान्तर चतुर्भुज और एक समद्विबाहु त्रिभुज
(iii)एक वर्ग और एक समान्तर चतुर्भुज
(iv)एक आयत और एक समचतुर्भुज
(v)एक समचतुर्भुज और एक समान्तर चतुर्भुज
उपर्युक्त सवालों को हल करने पर समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Area of Parallelograms and Triangle),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms and Triangle Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Mid-Point Theorem Class 9
4.समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Frequently Asked Questions Related to Area of Parallelograms and Triangles),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms and Triangles Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.संगत तलीय क्षेत्र किसे कहते हैं? (What is the Corresponding Planner Region?):
उत्तर:एक सरल बन्द आकृति (simple closed figure) द्वारा तल का घेरा हुआ भाग उस आकृति का संगत तलीय क्षेत्र (planner region) कहलाता है।इस तलीय क्षेत्र का परिणाम (magnitude) या माप (measure) उस आकृति का क्षेत्रफल (area) कहलाता है।इस परिमाण या माप को सदैव एक संख्या [किसी मात्रक (unit) में] की सहायता से व्यक्त किया जाता है।जैसेः5 वर्ग सेमी,8 वर्गमीटर, 3 हेक्टेयर इत्यादि।
प्रश्न:2.क्या सर्वांगसम आकृतियों का क्षेत्रफल समान होता है? (Do Congruent Figures Have the Same Area?):
उत्तर:दो आकृतियाँ A और B सर्वांगसम हैं तो उनके क्षेत्रफल अवश्य ही बराबर (समान) होने चाहिए।
सर्वांगसम आकृतियों की अवधारणा से आप परिचित हैं कि दो आकृतियाँ सर्वांगसम कही जाती हैं यदि उनके आकार (shape) और माप (size) समान हों।
प्रश्न:3.क्या समान क्षेत्रफल वाली आकृतियाँ सर्वांगसम होती हैं? (Are Figures with the Same Area All the Congruent?):
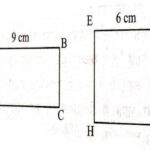
उत्तर:बराबर क्षेत्रफलों वाली दो आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
उदाहरणार्थ आयतों ABCD और EFGH के क्षेत्रफल 9×4 वर्गसेमी और 6×6 वर्गसेमी बराबर हैं परन्तु स्पष्टतः ये सर्वांगसम नहीं हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Area of Parallelograms and Triangle),समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms and Triangles Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Area of Parallelograms and Triangles
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
(Area of Parallelograms and Triangles)
Area of Parallelograms and Triangles
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Area of Parallelograms and Triangles) के इस
आर्टिकल में विभिन्न आकृतियों जैसे आयत,वर्ग,समान्तर चतुर्भुज,त्रिभुज इत्यादि आकृतियों के
क्षेत्रफलों के बीच सम्बन्ध का
About Author
Satyam
Lekhak Ke Baare Mein (About the Author) **Satyam Narain Kumawat** **Website Name:Satyam Mathematics** *Owner:satyamcoachingcentre.in* *Sthan:Manoharpur,Jaipur (Rajasthan)* **Teaching Mathematics aur Anya Anubhav** ***Shiksha:**B.sc.,B.Ed.,(M.sc. star Ke Mathematics Ko Padhane ka Anubhav),B.com.,M.com. Ke vishayon Ko Padhane ka Anubhav,Philosophy,Psychology,Religious,sanskriti Mein Gahri Ruchi aur Adhyayan ***Anubhav:**phichale 23 varshon se M.sc.,M.com.,Angreji aur Vigyan Vishayon Mein Shikshaka Ka Lamba Anubhav ***Visheshagyata:*Maths,Adhyatma (spiritual),Yog vishayon ka vistrit Gyan* ****In Brief:I have read about M.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 23 years teaching experience upto M.sc. ,M.com.,English and science.
