Area of Closed Curve in Integrals
1.समाकल में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integrals),समाकल गणित में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integral Calculus):
- समाकल में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integrals) ज्ञात करने के लिए प्राचल समीकरणों का प्रयोग करेंगे।हालांकि प्राचलिक समीकरणों को कार्तीय निर्देशांकों में परिवर्तित करके क्षेत्रफल ज्ञात किया जा सकता है।
- बन्द वक्र का क्षेत्रफल (Area of Closed Curve):
बन्द वक्र x=f_{1}\left(t\right),y=f_{2}\left(t\right) का क्षेत्रफल \frac{1}{2}\int_{t_{1}}^{t_{2}}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt होता है।
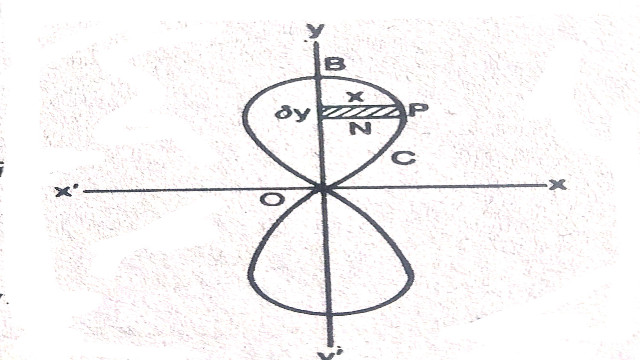
- मानलो वक्र AP’BPA एक बन्द वक्र है तथा x=f_{1}\left(t\right),y=f_{2}\left(t\right) इसके समीकरण हैं जहाँ f_{1}\left(t\right)\text{ तथा }f_{2}\left(t\right) चर t के एक-मानीय फलन (single valued function) है और प्रत्येक रेखा जो y-अक्ष के समान्तर (parallel) है इसके केवल दो बिन्दुओं पर मिलती है।
- क्योंकि वक्र बन्द है और f_{1}\left(t\right)\text{ तथा }f_{2}\left(t\right) चर t के एक-मानीय फलन है, इसलिए जैसे-जैसे बिन्दु P वक्र के अनुदिश (along) गमन करता है t का मान सतत (continuously) बदलता है और P जहाँ से चालू होता है वहाँ पर आकर दुबारा मिलता है।अतः वक्र के एक बिन्दु के लिए t के दो मान होंगे।मानलो बिन्दु P के लिए t के दो मान व है।मानलो AD व BC,y-अक्ष के समान्तर वक्र पर दो स्पर्श रेखाएँ (tangents) इस प्रकार है कि OD=a तथा OC=b जहाँ b>a है।
- मानलो y-अक्ष के समान्तर रेखा LRQ वक्र को दो बिन्दुओं R व Q पर इस प्रकार मिलती है कि LQ>LR मानलो OL=x।यह भी मानलो कि बिन्दुओं A व B के लिए t के मान क्रमशः t_{3}\text{ व }t_{4} है।मानलो वक्र द्वारा घिरा हुआ क्षेत्रफल A है।
- अभीष्ट क्षेत्रफल (A)=क्षेत्रफल DAQBCD-क्षेत्रफल DARBCD
=\int_{a}^{b}\text{QL } dx-\int_{a}^{b}\text{RL } dx
अब \int_{a}^{b}\text{QL } dx=\int_{t_{3}}^{t_{4}}y\frac{dx}{dt} dt
=-\int_{t_{4}}^{t_{3}}y\frac{dx}{dt}dt
और \int_{a}^{b}\text{RL } dx=\int_{a}^{x}\text{RL } dx+\int_{x}^{b}\text{RL }dx
=\int_{t_{1}}^{t_{2}}y\frac{dx}{dt} dt+\int_{t_{1}}^{t_{4}}y\frac{dx}{dt} dt
A=-\int_{t_{4}}^{t_{3}}y\frac{dx}{dt}dt-\int_{t_{1}}^{t_{2}}y\frac{dx}{dt}dt-\int_{t_{2}}^{t_{4}}y\frac{dx}{dt}dt
=-[\int_{t_{1}}^{t_{4}}y\frac{dx}{dt}dt+\int_{t_{4}}^{t_{3}}y\frac{dx}{dt}dt+\int_{t_{3}}^{t_{2}}y\frac{dx}{dt}dt]
=-\int_{t_{1}}^{t_{2}}y\frac{dx}{dt}dt …(1)
इसी प्रकार x-अक्ष के समान्तर वक्र पर स्पर्श रेखाएँ खींचकर हम सिद्ध कर सकते हैं कि:
A=\int_{t_{1}}^{t_{2}}x\frac{dy}{dt}.dt …(2)
(1) और (2) को जोड़ने पर हमें प्राप्त होता है:
2A=\int_{t_{1}}^{t_{2}}x\frac{dy}{dt}.dt-\int_{t_{1}}^{t_{2}}y\frac{dx}{dt}dt …(1)
या A=\frac{1}{2}\int_{t_{1}}^{t_{2}}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt - आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:SA of Solids of Revolution
2.समाकल में बन्द वक्र का क्षेत्रफल पर आधारित उदाहरण (Examples Based on Area of Closed Curve in Integrals):
Example:1.निम्नलिखित वक्रों से घिरे हुए क्षेत्रफल ज्ञात कीजिए:
(Find the area enclosed by the following curves):
(a):x=a\cos{t}+b\sin{t}+c,x=a'\cos{t}+b'\sin{t}+c'
Solution:x=a\cos{t}+b\sin{t}+c,x=a'\cos{t}+b'\sin{t}+c'
t=0 पर x=a+c,y=a’+c’
तथा t={2\pi} पर x=a+c,y=a’+c’
अतः दिया हुआ वक्र एक बन्द वक्र है और t=0 से के मध्य इसका अनुरेख किया जा सकता है।
अब वक्रों के समीकरण के समीकरण का t के सापेक्ष अवकलन करने पर:
\frac{dx}{dt}=-a\sin{t}+b\cos{t}
तथा \frac{dx}{dt}=-a'\sin{t}+b'\cos{t}
अतः अभीष्ट क्षेत्रफल=\frac{1}{2}\int_{0}^{2\pi}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=\frac{1}{2}\int_{0}^{2\pi}[\left(a\cos{t}+b\sin{t}+c\right)\left(-a'\sin{t}+b'\cos{t}\right)\\-\left(a'\cos{t}+b'\sin{t}+c'\right)\left(-a\sin{t}+b\cos{t}\right)]dt
=\frac{1}{2}\int_{0}^{2\pi}[-aa'\cos{t}\sin{t}-a'b\sin^{2}t-a'c\sin{t}+ab'\cos^{2}t+bb'\sin{t}\cos{t}+\\b'c\cos{t}+aa'\sin{t}\cos{t}+ab'\sin^{2}t+ac'\sin{t}-a'b\cos^{2}t-bb'\sin{t}\cos{t}-bc'\cos{t}]dt
=\frac{1}{2}\int_{0}^{2\pi}[-a'b\left(\sin^{2}t+\cos^{2}t\right)+ab'\left(\sin^{2}t\\+\cos^{2}t\right)-a'c\sin{t}+b'c\cos{t}+ac'\sin{t}-bc'\cos{t}]dt
=\frac{1}{2}\int_{0}^{2\pi}[-a'b+ab'-a'c\sin{t}+b'c\cos{t}+ac'\sin{t}-bc'\cos{t}]dt
\frac{1}{2}\left[\left(-a'b+ab'\right)t\right]_{0}^{2\pi}+\frac{1}{2}\left[a'c\cos{t}+b'c\sin{t}-ac'\cos{t}-bc'\sin{t}\right]_{0}^{2\pi}
\frac{1}{2}\left(-a'b+ab'\right)×{2\pi}+\frac{1}{2}\left[a'c-ac'-a'c+ac'\right]
\left(-a'b+ab'\right)×{\pi}
(b):x=a\left(3\sin{t}-\sin^{3}t\right),y=a\cos^{3}t
Solution:x=a\left(3\sin{t}-\sin^{3}t\right),y=a\cos^{3}t
t=0 पर x=0,y=a
t={2\pi} पर x=0,y=a
अतः दिया हुआ वक्र एक बन्द वक्र है और इसका अनुरेख किया जा सकता है जब
{0}\leq{t}\leq{2\pi}
अब वक्रों के समीकरण का t के सापेक्ष अवकलन करने पर:
\frac{dx}{dt}=a\left(3\cos{t}-3\sin^{2}t\cos{t}\right)
\frac{dy}{dt}=-3a\cos^{2}\sin{t}
अभीष्ट क्षेत्रफल=\frac{1}{2}\int_{0}^{2\pi}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=\frac{1}{2}\int_{0}^{2\pi}[a\left(3\sin{t}-\sin^{3}t\right)\left(-3a\cos^{2}t\sin{t}\right)-a\cos^{3}t\left[a\left(3\sin{t}-\sin^{3}t\right)\right]dt
=\frac{1}{2}\int_{0}^{2\pi}\left[-9\sin^{2}t\cos^{2}t+3\sin^{4}t\cos^{2}t-3\cos^{3}t\sin{t}\\+\sin^{3}t\cos^{3}t\right]dt
=\frac{1}{2}\int_{0}^{2\pi}\left(-9\sin^{2}t\cos^{2}t\right)dt+\frac{3a^{2}}{2}\int_{0}^{2\pi}\sin^{4}t\cos^{2}tdt-\frac{a^{2}}{2}\int_{0}^{2\pi}3\cos^{3}t\sin{t}dt+\frac{a^{2}}{2}\int_{0}^{2\pi}\sin^{3}t\cos^{3}tdt
=-\frac{9a^{2}}{2}×4\int_{0}^{2\pi}\sin^{2}t\cos^{2}tdt+\frac{3a^{2}}{2}×4\int_{0}^{2\pi}\sin^{4}t\cos^{2}t-\frac{3a^{2}}{2}\int_{0}^{2\pi}\cos^{3}t\sin{t}dt+\frac{a^{2}}{2}\int_{0}^{2\pi}\sin^{3}t\cos^{3}tdt \left[\because{f\left({2\pi}-t\right)}=f\left(t\right)\right]
=-18a^{2}\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{2+2+2}{2}\right)}}+6a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{4+2+2}{2}\right)}}+\frac{3a^{2}}{2}\left[\frac{\cos^{4}t}{4}\right]_{0}^{2\pi}+\frac{a^{2}}{2}\int_{0}^{2\pi}\left(\sin^{3}t-\sin^{5}t\right)\cos{t}dt
=-9a^{2}\frac{\frac{1}{2}\sqrt{\pi}\frac{1}{2}\sqrt{\pi}}{2}+3a^{2}\frac{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}\frac{1}{2}\sqrt{\pi}}{3×2×1}+\frac{3a^{2}}{2}×0+\frac{a^{2}}{2}\left[\frac{\sin^{4}t}{4}-\frac{\sin^{6}t}{6}\right]_{0}^{2\pi}
=-\frac{9{\pi}a^{2}}{16}+\frac{3{\pi}a^{2}}{16}+0+0
=\frac{-18{\pi}a^{2}+3{\pi}a^{2}}{16}
=\frac{15{\pi}a^{2}}{16}
(c):x=\frac{1-t^{2}}{1+t^{2}},y=\frac{2t}{1+t^{2}}
Solution:x=\frac{1-t^{2}}{1+t^{2}},y=\frac{2t}{1+t^{2}}
जब t=1 तो x=0,y=0 जब t=-1 तो x=0,y=-1
अतः दिया हुआ वक्र एक बन्द वक्र है और इसका अनुरेख किया जा सकता है जब अब वक्रों के समीकरण का t के सापेक्ष अवकलन करने पर:
\frac{dx}{dt}=\frac{\left(1+t^{2}\right)\left(-2t\right)-\left(1-t^{2}\right)2t}{\left(1+t^{2}\right)^{2}}
=\frac{-2t-2t^{3}-2t+2t^{3}}{\left(1+t^{2}\right)^{2}} =\frac{-4t}{\left(1+t^{2}\right)^{2}}
\frac{dy}{dt}=\frac{\left(1+t^{2}\right).2-2t.2t}{\left(1+t^{2}\right)^{2}}
=\frac{dy}{dt}=\frac{2+2t^{2}-4t^{2}}{\left(1+t^{2}\right)^{2}} =\frac{2-2t^{2}}{\left(1+t^{2}\right)^{2}} =\frac{2\left(1-t^{2}\right)}{\left(1+t^{2}\right)^{2}}
अभीष्ट क्षेत्रफल=\frac{1}{2}\int_{-1}^{1}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=2×\frac{1}{2}\int_{-1}^{1}\left[\frac{1-t^{2}}{1+t^{2}}×\frac{2\left(1+t^{2}\right)}{\left(1+t^{2}\right)^{2}}-\frac{2t}{1+t^{2}}.\frac{-4t}{\left(1+t^{2}\right)^{2}}\right]dt
=\int_{-1}^{1}\left[\frac{2\left(1-t^{2}\right)^{2}}{\left(1+t^{2}\right)^{3}}+\frac{8t^{2}}{\left(1+t^{2}\right)^{3}}\right]dt
=2\int_{-1}^{1}\left[\frac{1+t^{4}-2t^{2}+4t^{2}}{\left(1+t^{2}\right)^{3}}\right]dt
=2\int_{-1}^{1}\frac{\left(1+2t^{2}+t^{4}\right)}{\left(1+t^{2}\right)^{3}}dt
=2\int_{-1}^{1}\frac{\left (1+t^{2}\right)^{2}}{\left(1+t^{2}\right)^{3}}dt
=2\int_{-1}^{1}\frac{1}{1+t^{2}}dt
=2\left[\tan^{-1}t\right]_{-1}^{1}
=2\left[\tan^{-1}\left(1\right)-\tan^{-1}\left(-1\right)\right]
=2\left(\frac{\pi}{4}+\frac{\pi}{4}\right)
={\pi}
(d):x=\frac{a\left(1-t^{2}\right)}{1+t^{2}},y=\frac{2at}{1+t^{2}}
Solution:x=\frac{a\left(1-t^{2}\right)}{1+t^{2}},y=\frac{2at}{1+t^{2}}
जब t=1 तो x=0,y=a जब t=-1 तो x=0,y=-a
अतः दिया हुआ वक्र एक बन्द वक्र है और इसका अनुरेख किया जा सकता है जब अब वक्रों के समीकरण का t के सापेक्ष अवकलन करने पर:
\frac{dx}{dt}=a\left[\frac{\left(1+t^{2}\right)\left(-2t\right)-\left(1-t^{2}\right)2t}{\left(1+t^{2}\right)^{2}}\right]
=a\frac{\left[-2t-2t^{3}-2t+2t^{3}\right]}{\left(1+t^{2}\right)^{2}} =\frac{-4at}{\left(1+t^{2}\right)^{2}}
\frac{dy}{dt}=2a\left[\frac{1+t^{2}-t.2t}{\left(2+t^{2}\right)^{2}}\right]
=2a\left[\frac{1-t^{2}}{\left(1+t^{2}\right)^{2}}\right]
अभीष्ट क्षेत्रफल=2×\frac{1}{2}\int_{-1}^{1}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=\int_{-1}^{1}\left[a\frac{\left(1-t^{2}\right)}{1+t^{2}}×2a\frac{\left(1-t^{2}\right)}{\left(2+t^{2}\right)^{2}}-\frac{2at}{1+t^{2}}.\left(\frac{-4at}{\left(1+t^{2}\right)^{2}}\right)\right]dt
=2a^{2}\int_{-1}^{1}\left[\frac{\left(1-t^{2}\right)^{2}}{\left(1+t^{2}\right)^{3}}+\frac{4t^{2}}{\left(1+t^{2}\right)^{3}}\right]dt
=2a^{2}\int_{-1}^{1}\left[\frac{1+t^{4}-2t^{2}+4t^{2}}{\left(1+t^{2}\right)^{3}}\right]
=2a^{2}\int_{-1}^{1}\left[\frac{1+2t^{2}+t^{4}}{\left(1+t^{2}\right)^{3}}\right]dt
=2a^{2}\int_{-1}^{1}\frac{\left(1+t^{2}\right)^{2}}{\left(1+t^{2}\right)^{3}}dt
=2a^{2}\int_{-1}^{1}\frac{1}{1+t^{2}}dt
=2a^{2}\left[\tan^{-1}t\right]_{-1}^{1}
=2a^{2}\left[\frac{\pi}{4}+\frac{\pi}{4}\right]
={\pi}a^{2}
Example:2.निम्नलिखित वक्रों के लूप का क्षेत्रफल ज्ञात कीजिए: (Find the area of the loop of the following curves):
(a):x=a\sin{2t},y=a\sin{t}
Solution:x=a\sin{2t},y=a\sin{t}
जब t=-\frac{\pi}{2} तो x=0,y=-a
जब t=\frac{\pi}{2} तो x=0,y=a
अतः दिया हुआ वक्र एक लूप बनाता है जब और इसका अनुरेख किया जा सकता है जब -\frac{\pi}{2}\leq{t}\leq{\frac{\pi}{2}}
अब वक्रों के समीकरण का t के सापेक्ष अवकलन करने पर:
\frac{dx}{dt}=2a\cos{2t}
\frac{dy}{dt}=a\cos{t}
अभीष्ट क्षेत्रफल=2×\frac{1}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=\frac{1}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\left(a\sin{2t}a\cos{t}-a\sin{t}2a\cos{2t}\right)dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\left(\cos{t}\sin{2t}-2\sin{t}\cos{2t}\right)dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\left[\sin{\left(2t-t\right)}-\sin{t}\cos{2t}\right]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\left[\sin{t}-\sin{t}\cos{2t}\right]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\sin{t}\left(1-\cos{2t}\right)dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}2\sin^{3}t dt
={a^{2}}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}\sin^{3}t dt
=2{a^{2}}\int_{0}^{\frac{\pi}{2}}\sin^{3}t dt
2a^{2}\frac{\Gamma{\left(\frac{3+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{3+0+2}{2}\right)}}
=a^{2}\frac{\sqrt{\pi}}{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}}
=\frac{4}{3}{\pi}a^{2}
(b):x=\frac{a\sin{3t}}{\sin{t}},y=\frac{a\sin{3t}}{\cos{t}}
Solution:x=\frac{a\sin{3t}}{\sin{t}},y=\frac{a\sin{3t}}{\cos{t}}
जब t=-\frac{\pi}{3} तो x=0,y=0
जब t=\frac{\pi}{3} तो x=0,y=0
अतः दिया हुआ वक्र एक लूप बनाता है जब और इसका अनुरेख किया जा सकता है जब -\frac{\pi}{3}\leq{t}{\frac{\pi}{3}}
अब वक्रों के समीकरण का t के सापेक्ष अवकलन करने पर:
x=\frac{a\sin{3t}}{\sin{t}}
=a\frac{\left(3\sin{t}-4\sin^{3}t\right)}{\sin{t}}
=a\left(3-4\sin^{2}t\right)
\frac{dx}{dt}=-8\sin{t}\cos{t}
y=\frac{a\sin{3t}}{\cos{t}}
=y=\frac{a\left(3\sin{t}-4\sin^{3}t\right)}{\cos{t}}
\frac{dy}{dt}=\frac{a\left[\cos{t}\left(3\cos{t}-12\sin^{2}{t}\cos{t}\right)-\left(-\sin{t}\right)\left(3\sin{t}-4\sin^{3}t\right)\right]}{\cos^{2}t}
=\frac{a\left[3\cos^{2}t+3\sin^{2}t-12\sin^{2}t\cos^{2}t+4\sin^{4}t\right]}{\cos^{2}t}
=\frac{a\left(8\cos^{4}t-4\cos^{2}t-4\sin^{4}t\right)}{\cos^{2}t}
=\frac{a\left(8\cos^{4}t-4\cos^{2}t-4\sin^{4}t\right)}{\cos^{2}}
x=a\left(3-4\sin^{t}\right)
=a\left(3-4\left(1-\cos^{2}t\right)\right)
=a\left(4\cos^{2}t-1\right)
अभीष्ट क्षेत्रफल=\frac{1}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=\frac{1}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}[a\left(4\cos^{2}t-1\right)\frac{a\left(8\cos^{4}t-4\cos^{2}t-4\sin^{4}t\right)}{\cos^{2}}-\frac{a\sin{3t}}{\cos{t}}\left(-8a\sin{t}\cos{t}\right)]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}\left[\frac{32\cos^{6}t-24\cos^{4}t+1}{\cos^{2}t}+8\left(3\sin^{2}t-4\sin^{4}t\right)\right]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}[32\cos^{4}t-24\cos^{2}t+\sec^{2}t+24\left(\frac{1-\cos{2t}}{2}\right)-32\left(\frac{1-cos{2t}}{2}\right)]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}32\left(\frac{1+\cos{2t}}{2}\right)^{2}-24\left(\frac{1+\cos{2t}}{2}\right)+\sec^{2}t+12-12\cos{2t}-8-8\cos^{2}2t+16\cos{2t}]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}[8+16\cos{2t}+8\cos^{2}2t-12-12\cos{2t}+\sec^{2}t+4+4\cos{2t}-8\cos^{2}2t]dt
=\frac{a^{2}}{2}\int_{\frac{-\pi}{3}}^{\frac{\pi}{3}}[8\cos{2t}+\sec^{2}t]dt
=\frac{a^{2}}{2}\left[4\sin{2t}+\tan{t}\right]_{\frac{-\pi}{3}}^{\frac{\pi}{3}}
=\frac{a^{2}}{2}\left[\frac{4\sqrt{3}}{2}+\frac{4\sqrt{3}}{2}+\sqrt{3}+\sqrt{3}\right]
=\frac{a^{2}}{2}\left[8\sqrt{3}\right]
=3\sqrt{3}a^{2}
(c):x=\frac{3at}{1+t^{3}},y=\frac{3at^{2}}{1+t^{3}}
Solution:x=\frac{3at}{1+t^{3}},y=\frac{3at^{2}}{1+t^{3}}
जब t=0 तो x=0,y=0 जब t=1 तो x=\frac{3a}{2},y=\frac{3a}{2}
अतः दिया हुआ वक्र एक लूप बनाता है जब और इसका अनुरेख किया जा सकता है जब 1\leq{t}\leq{0} अब वक्रों के समीकरण का t के सापेक्ष अवकलन करने पर:
\frac{dx}{dt}=\frac{3a\left(1-2t^{3}\right)}{\left(1+t^{3}\right)^{2}} \frac{dy}{dt}=\frac{3a\left(2t-t^{4}\right)}{\left(1+t^{3}\right)^{2}}
अभीष्ट क्षेत्रफल=\frac{1}{2}\int{1}^{0}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
=\frac{1}{2}\int_{1}^{0}[\frac{3at}{\left(1+t^{3}\right)}.\frac{3a\left(2t-t^{4}\right)}{\left(1+t^{3}\right)^{2}}-\frac{3at^{2}}{\left(1+t^{3}\right)}.\frac{3a\left(1-2t^{3}\right)}{\left(1+t^{3}\right)^{2}}]dt
=\frac{9a^{2}}{2}\int_{1}^{0}\frac{\left(2t^{2}-t^{5}-t^{2}+2t^{5}\right)}{\left(1+t^{3}\right)^{3}}dt
=\frac{9a^{2}}{2}\int_{1}^{0}\frac{\left(t^{2}+t^{5}\right)}{\left(1+t^{3}\right)^{3}}dt
=\frac{9a^{2}}{2}\int_{1}^{0}\frac{t^{2}\left(1+t^{3}\right)}{\left(1+t^{3}\right)^{3}}dt
=\frac{9a^{2}}{2}\int_{1}^{0}\frac{t^{2}}{\left(1+t^{3}\right)^{2}}
=\frac{3a^{2}}{2}\left[-\frac{1}{1+t^{3}}\right]{1}^{0}
=\frac{3a^{2}}{2}
उपर्युक्त उदाहरणों के द्वारा समाकल में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integrals),समाकल गणित में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integral Calculus) को समझ सकते हैं।
Also Read This Article:Area Bounded by Plane Curves
3.समाकल में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integrals),समाकल गणित में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integral Calculus) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
Area of Closed Curve in Integrals,Area of Closed Curve in Integral Calculus,Write the formula to find the area of the closed curve,Write the formula to find the mass from the double integral in the Quadrature,Write down the formula to find the area bounded by curves and straight lines
प्रश्न:1.वक्रों तथा सरल रेखाओं से परिबद्ध क्षेत्रफल ज्ञात करने के सूत्र लिखो।(Write down the formula to find the area bounded by curves and straight lines):
उत्तर:(1)कार्तीय वक्र y=f(x),x-अक्ष और x=a तथा x=b कोटियों द्वारा घिरा क्षेत्रफल=\int_{a}^{b} ydx
(2.)दो कार्तीय वक्रों द्वारा घिरा क्षेत्रफल=\int_{a}^{b} f_{1}(x)dx–\int_{c}^{d} f_{2}(x)dx
(3.)ध्रुवीय समीकरणों वाले वक्रों तथा ध्रुवान्तर रेखाओं से परिबद्ध क्षेत्रफल ज्ञात करने का सूत्र=
\int_{\alpha}^{\beta} r^{2}{d\theta}
(4.)कार्तीय समीकरणों को प्राचलिक समीकरणों में बदलकर क्षेत्रफल ज्ञात करने का सूत्र=
\int_{t=\alpha}^{t=\beta} y\frac{dx}{dt}.dt अथवा \int_{t=\alpha}^{t=\beta} x\frac{dy}{dt}.dt
प्रश्न:2.बन्द वक्र का क्षेत्रफल ज्ञात करने का सूत्र लिखो।(Write the formula to find the area of the closed curve):
उत्तर:\frac{1}{2}\int{a}^{b}\left(x\frac{dy}{dt}-y\frac{dx}{dt}\right)dt
प्रश्न:3.क्षेत्रकलन में द्वि-समाकल से द्रव्यमान ज्ञात करने का सूत्र लिखो।(Write the formula to find the mass from the double integral in the Quadrature):
उत्तर:द्रव्यमान (Mass):
कार्तीय निर्देशांकों में यदि किसी पतली चद्दर की प्लेट के किसी बिन्दु (x,y) पर द्रव्यमान प्रति इकाई क्षेत्र (mass per unit area) या घनत्व (density) {\rho}=f(x,y) हो तो उसका कुल द्रव्यमान होगा:
M={\int}\int_{A}{\rho}dA={\int}\int_{A}f(x,y) dA …(4)
ध्रुवीय निर्देशांकों में यदि {\rho}=f\left(r,{\theta}\right)r{d\theta} हो तो
M={\int}\int_{A}{\rho}dA={\int}\int_{A}f\left(r,{\theta}\right)r{d\theta}dr …(5)
द्वि-समाकल से पृष्ठ के अन्तर्गत आयतन (Volume under Surface by Double Integration):
xy समतल पर आधार A के ऊपर पृष्ठ z=f(x,y) के अन्तर्गत आयतन V,द्वि-समाकलन के रूप में निम्न प्रकार लिखा जा सकता है:
V={\int}\int_{A}z dA
यदि क्षेत्र A निम्न वक्रों द्वारा घिरा हुआ हो
y=f_{1}(x),y=f_{2}(x),x=a तथा x=b हो तो:
V=\int_{a}^{b}\int_{f_{1}(x)}^{f_{2}(x)} z dxdy=\int_{a}^{b}\int_{f_{1}(x)}^{f_{2}(x)} f(x,y)dxdy
- उपर्युक्त प्रश्नों के उत्तर द्वारा समाकल में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integrals),समाकल गणित में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integral Calculus) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Area of Closed Curve in Integrals
समाकल में बन्द वक्र का क्षेत्रफल
(Area of Closed Curve in Integrals)
Area of Closed Curve in Integrals
समाकल में बन्द वक्र का क्षेत्रफल (Area of Closed Curve in Integrals) ज्ञात करने के लिए प्राचल
समीकरणों का प्रयोग करेंगे।हालांकि प्राचलिक समीकरणों को कार्तीय निर्देशांकों में परिवर्तित करके क्षेत्रफल ज्ञात किया जा सकता है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |