1.समतल वक्रों द्वारा परिबद्ध क्षेत्रफल (Area Bounded by Plane Curves),समतल वक्रों द्वारा परिबद्ध क्षेत्रकलन (Quadrature Bounded by Plane Curves):

समतल वक्रों द्वारा परिबद्ध क्षेत्रफल (Area Bounded by Plane Curves) को क्षेत्रकलन भी कहते हैं अर्थात् वक्रों (Curves) अथवा सरल रेखाओं (Straight Line) अथवा दोनों से घिरे क्षेत्र का क्षेत्रफल ज्ञात करने की विधि को क्षेत्रकलन (Quadrature) कहते हैं।
वक्रों का कार्तीय समीकरण (Cartesian Equation of Curves):

वक्र y=f(x),x-अक्ष और x=a तथा x=b कोटियों द्वारा घिरा हुआ क्षेत्रफल \int_{a}^{b}f(x) dx अथवा \int_{a}^{b}y dx होता है
(The area bounded by the curve y=f(x), the axis of x and the ordinates x=a and x=b is given by \int_{a}^{b}f(x) dx or \int_{a}^{b}y dx.)
मान लो वक्र y=f(x) पर दो बिन्दु A और B हैं जहाँ f(x) प्रान्त (a,b) में x का कोई सतत फलन (continuous function) है और मानलो कि जैसे-जैसे x,a से b तक बढ़ता है वैसे-वैसे y भी बढ़ता चला जाता है।मानलो AD तथा BC वक्र की दो कोटियाँ x=a तथा x=b है।यहाँ हमें क्षेत्रफल ABCD ज्ञात करना है।
वक्र पर कोई बिन्दु P(x,y) लो और मानलो PL उसकी कोटि है।अब,वक्र पर P के समीप एक और बिन्दु Q\left(x+\delta{x},y+\delta{y}\right) लो और मानलो QM उसकी कोटि है।
अब P से QM तथा Q से LP बढ़ी हुई पर, क्रमशः PR तथा QS लम्ब खींचो।तब
OL=x,OM=x+\delta{x}
\text{ LM }=\delta{x}
PL=y,QM=y+\delta{y}
\therefore \text{ QR }=\delta{y}
मानलो A तथा A+\delta{A} क्रमशः क्षेत्रफल APLD तथा AQMD को प्रदर्शित करते हैं, तो
\delta{A}=क्षेत्रफल AQMD-क्षेत्रफल APLD= क्षेत्रफल PQML
परन्तु चित्र से स्पष्ट है कि क्षेत्रफल PQML,आयतों SQML तथा PRML के बीच में स्थित है अर्थात्
क्षेत्रफल PRML< क्षेत्रफल PQML<क्षेत्रफल SQML

\because y\delta{x}<\delta{A}<\left(y+\delta{y}\right)\delta{x}

\text{ या }y<\frac{\delta{A}}{\delta{x}}<\left(y+\delta{y}\right)…(1)

जब बिन्दु Q बिन्दु P के बहुत समीप हो, सीमा में जब \delta{x}\rightarrow{0} तो \delta{y}\rightarrow{0} और तब (1) की सीमा लेने पर:

\lim_{\delta{x}\rightarrow{0}}y<\lim_{\delta{x}\rightarrow{0}}\frac{\delta{A}}{\delta{x}}<\lim_{\delta{x}\rightarrow{0}}\left(y+\delta{y}\right)

\therefore y<\frac{dA}{dx}<y\quad{\left[\because {\delta{x}\rightarrow{0}},{\delta{y}\rightarrow{0}}\right]}

\text{ अर्थात् }\frac{dA}{dx}=y=f{x} …(2)

अब दोनों पक्षों का x के सापेक्ष x=a तथा x=b सीमाओं के बीच समाकलन करने पर:

\int_{a}^{b}dx=\int_{a}^{b}\frac{dA}{dx}. dx

=\left[A\right]_{a}^{b}

=[A का मान जब x=b]-[A का मान जब x=a]

=क्षेत्रफल ABCD-0

=क्षेत्रफल ABCD

अतः क्षेत्रफल ABCD=\int_{a}^{b}dx=\int_{a}^{b}y dx

टिप्पणी:उपर्युक्त विधि को काम में लेकर हम यह सिद्ध कर सकते हैं कि वक्र \phi{y},y-अक्ष और y=c तथा y=d भुजों (abscissae) द्वारा घिरा हुआ क्षेत्रफल \int_{c}^{d}\phi{y}dy अथवा \int_{c}^{d} xdy होता है। (2.)कभी-कभी वक्र के कार्तीय समीकरण (Cartesian Equation) को प्राचलिक समीकरण (Parametric Equation) में बदलकर क्षेत्रफल आसानी से निकाला जा सकता है।इसके लिए हम निम्न सूत्र काम में लेते हैं:

\int_{t=\alpha{}}^{t=\beta{}}y\frac{dx}{dt}\text{ अथवा }\int_{t=\alpha{}}^{t=\beta{}}x\frac{dy}{dt}.dt

(3.)यदि दिया हुआ वक्र किसी एक अक्ष के सापेक्ष सममित (Symmetrical) हो तो वक्र का क्षेत्रफल अक्ष के एक ओर का क्षेत्रफल ज्ञात कर उसको 2 से गुणा कर देते हैं।

(4.)यदि दिया हुआ वक्र दोनों के सापेक्ष सममित (Symmetrical) हो तो किसी एक पाद (quadrant) में वक्र का क्षेत्रफल निकालकर उसको 4 से गुणा कर देते हैं।ऐसा करना इसलिए आवश्यक है क्योंकि यदि हम वक्र द्वारा घिरे हुए सम्पूर्ण क्षेत्र का क्षेत्रफल केवल समाकलन से ज्ञात करें तो उसका बीजीय क्षेत्रफल शून्य आयेगा क्योंकि प्रथम,द्वितीय, तृतीय तथा चतुर्थ पादों में क्षेत्रफल क्रमशः धनात्मक, ऋणात्मक, धनात्मक तथा ऋणात्मक होता है।

दो कार्तीय वक्रों से परिबद्ध क्षेत्रफल (Area Bounded by Two Cartesian Curves):

मानलो y=f_{1}(x) और y=f_{1}(x) वक्रों APB तथा AQB को निरूपित करते हैं जो कि बिन्दुओं x=a और x=b पर एक दूसरे को काटते हैं। अब दोनों वक्रों द्वारा घिरा हुआ क्षेत्रफल APBQA=क्षेत्रफल APBDC-क्षेत्रफल AQBDC

=\int_{a}^{b}f_{1}(x)-\int_{a}^{b}f_{2}(x)dx

=\int_{a}^{b}\left[f_{1}(x)-f_{2}(x)\right]dx

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:Surface Area of Solids of Revolution

2.समतल वक्रों द्वारा परिबद्ध क्षेत्रफल पर आधारित उदाहरण (Examples Based on Area Bounded by Plane Curves):

Example:1.निम्नलिखित वक्रों x-अक्ष और दी हुई कोटियों से घिरे हुए क्षेत्रफल ज्ञात कीजिए: (Find the area bounded by the axis, ordinates and the following curves):

(a):y=\log_{e}{x}x=a,x=b (b>a>1)
Solution:y=\log_{e}{x} x=a,x=b (b>a>1)
अभीष्ट क्षेत्रफल=
=\int_{a}^{b}ydx
=\int_{a}^{b}\log_{e}{x} dx
=\left[x\log_{e}{x}\right]_{a}^{b}-\left[x\right]_{a}^{b}

=b\log_{e}b-a\log_{e}{a}-b+a
=b\log_{e}b-a\log_{e}{a}-b\log_{e}{e}+a\log_{e}{e}
=b\log_{e}\left(\frac{b}{e}\right)-a\log_{e}\left(\frac{a}{e}\right)

(b):y=c\cosh{\left(\frac{x}{c}\right)};x=0,x=a [catenary]
Solution:y=c\cosh{\left(\frac{x}{c}\right)};x=0,x=a
अमीष्ट क्षेत्रफल=
=\int_{0}^{a}dx
=\int_{0}^{a}c\cosh{\left(\frac{x}{c}\right)}dx
=c^{2}\left[\cosh{\left(\frac{x}{c}\right)}\right]_{0}^{a}

=c^{2}\cosh{\left(\frac{a}{c}\right)}

(c):xy=c^{2};x=a,x=b (a>b) [Hyperbola]

Solution:xy=c^{2}

अभीष्ट क्षेत्रफल=

=\int_{b}^{a} ydx

=\int_{b}^{a}\frac{c^{2}}{x}
=c^{2}\left[\log_{e}{x}\right]_{b}^{a}

=c^{2}\left(\log_{e}{a}-\log_{e}{b}\right)

=c^{2}\log_{e}\left(\frac{a}{b}\right)
(d):y=\tan{x};x=-\frac{\pi}{3},x=\frac{\pi}{3}
Solution:y=\tan{x};x=-\frac{\pi}{3},x=\frac{\pi}{3}
अभीष्ट क्षेत्रफल=
=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}ydx
=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\tan{x}dx

=2\int_{0}^{\frac{\pi}{3}}\tan{x}dx

=2\left[\log{\sec{x}}\right]_{0}^{\frac{\pi}{3}}
=2\log{2}
Example:2.निम्नलिखित वक्रों का सम्पूर्ण क्षेत्रफल ज्ञात कीजिए:
(Find the whole area of the following curves):
(a):\left(\frac{x}{a}\right)^{\frac{2}{3}}+\left(\frac{y}{b}\right)^{\frac{2}{3}}=1 [Hypo-cycloid]

Solution:\left(\frac{x}{a}\right)^{\frac{2}{3}}+\left(\frac{y}{b}\right)^{\frac{2}{3}}=1
माना x=a\cos^{3}{t},y=b\sin^{3}{t}
\frac{dx}{dt}=-3a\cos^{2}{t}\sin{t}
अभीष्ट क्षेत्रफल=
=4 × \int_{x=0}^{a} ydx
=4 \int_{t=\frac{\pi}{2}}^{0}y\left(\frac{dx}{dt}\right).dt
=4\int_{t=\frac{\pi}{2}}^{0}\left(b\sin^{3}{t}\right)\left(-3a\cos^{2}{t}\sin{t}\right)dt
=\int_{0}^{\frac{\pi}{2}}\sin^{4}{t}\cos^{2}{t}dt
=12ab\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{4+2+2}{2}\right)}}
=6ab.\frac{\Gamma{\left(\frac{5}{2}\right)}\Gamma{\left(\frac{3}{2}\right)}}{3.2.1}
=ab.\frac{3}{2}.\frac{1}{2}{\sqrt{\pi}}.\frac{1}{2}{\sqrt{\pi}}
=\frac{3{\pi}ab}{8}
(b):\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1

Solution:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
\Rightarrow \frac{y^{2}}{b^{2}}=1-\frac{x^{2}}{a^{2}}
\Rightarrow y^{2}=\frac{b^{2}}{a^{2}}\left(a^{2}-x^{2}\right)
\Rightarrow y=\frac{b}{a}\sqrt{a^{2}-x^{2}}
अभीष्ट क्षेत्रफल=4\int_{x=0}^{a}y dx
=4\int_{x=0}^{a}\frac{b}{a}\sqrt{\left(a^{2}-x^{2}\right)}dx
=\frac{4b}{a}\left[\frac{x}{2}\sqrt{\left(a^{2}-x^{2}\right)}+\frac{a^{2}}{2}\sin^{-1}\left(\frac{x}{a}\right)\right]_{0}^{a}

=\frac{4b}{a}\left[0+a^{2}\sin^{-1}\left(1\right)\right]

=\frac{4b}{a} × \frac{a^{2}}{2} × \frac{\pi}{2}

={\pi}ab

(c):a^{2}y^{2}=x^{3}\left(2a-x\right)

Solution:a^{2}y^{2}=x^{3}\left(2a-x\right)

y^{2}=\frac{x^{3}\left(2a-x\right)}{a^{2}}

\Rightarrow y=\frac{1}{a}\sqrt{x^{3}\left(2a-x\right)}

सीमा ज्ञात करने हेतु y=0 तो x=2a अभीष्ट क्षेत्रफल=

2\int_{0}^{2a}ydx

=2\int_{0}^{2a}\frac{1}{a}\sqrt{x^{3}\left(2a-x\right)}dx
\text{ Put }x=2a\sin^{2}{\theta}
\Rightarrow dx=4a\sin{\theta}\cos{\theta}{d\theta}
\text{ जब } x=0 \text{ तो }{\theta}=0
\text{ जब } x=2a \text{ तो }{\theta}=\frac{\pi}{2}
=\frac{2}{a}\int_{0}^{\frac{\pi}{2}}\sqrt{8a^{3}\sin^{6}{\theta}\left(2a-2a\sin^{2}{\theta}\right)}4a\sin{\theta}\cos{\theta}{d\theta}
=8\int_{0}^{\frac{\pi}{2}}\sqrt{16a^{4}\sin^{6}{\theta}\cos^{2}{\theta}}\sin{\theta}\cos{\theta}{d\theta}
=8\int_{0}^{\frac{\pi}{2}}4a^{2}\left(\sin^{3}{\theta}\cos{\theta}\right)\left(\sin{\theta}\cos{\theta}\right){d\theta}
=32a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{4}{\theta}\cos^{2}{\theta}{d\theta}
=32a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{4+2+2}{2}\right)}}
=16a^{2}\frac{\Gamma{\left(\frac{5}{2}\right)}\Gamma{\left(\frac{3}{2}\right)}}{\Gamma{4}}
=16a^{2}\frac{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}.\frac{1}{2}\sqrt{\pi}}{3 × 2 × 1}
=16a^{2}.\frac{\pi}{16}
={\pi}a^{2}
(d):a^{2}y^{2}=x^{2}\left(a^{2}-x^{2}\right)

Solution:a^{2}y^{2}=x^{2}\left(a^{2}-x^{2}\right)
y=\frac{x}{a}\sqrt{a^{2}-x^{2}}
अभीष्ट क्षेत्रफल=4 × \int_{0}^{a} ydx
=4 × \int_{0)}^{a}\frac{x}{a}\sqrt{a^{2}-x^{2}} dx
=\frac{4}{a} × \int_{0}^{a}x\sqrt{a^{2}-x^{2}} dx
\text{ Put }x=a\sin{\theta}
\Rightarrow dx=a\cos{\theta}{d\theta}
\text{ जब } x=0 \text{ तो }{\theta}=0
\text{ जब } x=a \text{ तो }{\theta}=\frac{\pi}{2}
=\frac{4}{a}\int_{0}^{\frac{\pi}{2}}\left(a\sin{\theta}\right)\sqrt{\left(a^{2}-a^{2}\sin^{2}{\theta}\right)}\left(a\cos{\theta}{d\theta}\right)
=4a^{2}\int_{0}^{\frac{\pi}{2}}\sin{\theta}\sqrt{1-\sin^{2}{\theta}}\cos{\theta}{d\theta}
=4a^{2}\int_{0}^{\frac{\pi}{2}}\sin{\theta}\cos^{2}{d\theta}
=4a^{2}\frac{\Gamma{\left(\frac{1+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{1+2+2}{2}\right)}}
=2a^{2}\frac{\Gamma{\left(1\right)}\Gamma{\left(\frac{3}{2}\right)}}{\Gamma{\left(\frac{5}{2}\right)}}
=2a^{2}\frac{\frac{1}{2}\sqrt{\pi}}{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}}
=\frac{4a^{2}}{3}
(e):a^{2}x^{2}=y^{3}\left(2a-y\right)

Solution:a^{2}x^{2}=y^{3}\left(2a-y\right)
x^{2}=\frac{y^{3}\left(2a-y\right)}{a^{2}}
\Rightarrow x=\frac{1}{a}\sqrt{y^{3}\left(2a-y\right)}
सीमा ज्ञात करने हेतु x=0 तो y=0,2a
अभीष्ट क्षेत्रफल=2\int_{0}^{2a}xdy
=2\int_{0}^{2a}\frac{1}{a}\sqrt{y^{3}\left(2a-y\right)}dy
\text{ Put }y=2a\sin^{2}{\theta}
\Rightarrow dy=4a\sin{\theta}\cos{\theta}{d\theta}
\text{ जब } y=0 \text{ तो }{\theta}=0
\text{ जब } y=2a \text{ तो }{\theta}=\frac{\pi}{2}
=\frac{2}{a}\int_{0}^{\frac{\pi}{2}}\sqrt{8a^{3}\sin^{6}{\theta}\left(2a-2a\sin^{2}{\theta}\right)}4a\sin{\theta}\cos{\theta}{d\theta}
=8\int_{0}^{\frac{\pi}{2}}\sqrt{16a^{4}\sin^{6}{\theta}\cos^{2}{\theta}}\sin{\theta}\cos{\theta}{d\theta}
=8\int_{0}^{\frac{\pi}{2}}4a^{2}\left(\sin^{3}{\theta}\cos{\theta}\right)\left(\sin{\theta}\cos{\theta}\right){d\theta}
=32a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{4}{\theta}\cos^{2}{\theta}{d\theta}
=32a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{4+2+2}{2}\right)}}
=16a^{2}\frac{\Gamma{\left(\frac{5}{2}\right)}\Gamma{\left(\frac{3}{2}\right)}}{\Gamma{4}}
=16a^{2}\frac{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}.\frac{1}{2}\sqrt{\pi}}{3 × 2 × 1}
=16a^{2}.\frac{\pi}{16}
={\pi}a^{2}
Example:3.निम्नलिखित वक्रों की पाशकुण्डली (लूप) का क्षेत्रफल ज्ञात कीजिए:
(Find the area of the loop of the following curves):
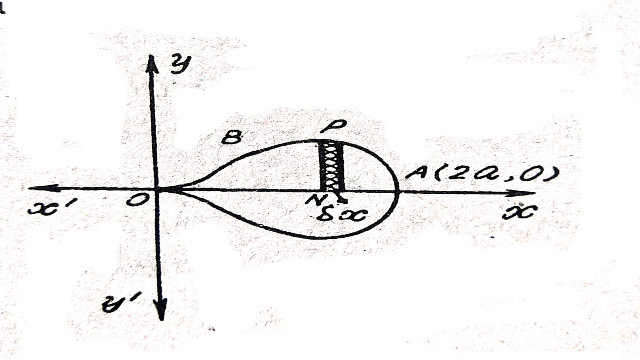
(a):ay^{2}=x^{2}\left(a-x\right)
Solution:ay^{2}=x^{2}\left(a-x\right)
y=\frac{x}{\sqrt{a}}\sqrt{a-x}
सीमा हेतु y=0 तो x=0,a
अभीष्ट क्षेत्रफल=2 × \int_{0}^{a} ydx
=2 × \int_{0}^{a}\sqrt{a-x} dx
\text{ Put }x=a\sin^{2}{\theta}
\Rightarrow dx=2a\sin{\theta}\cos{\theta}{d\theta}
\text{ जब } x=0 \text{ तो }{\theta}=0
\text{ जब } x=a \text{ तो }{\theta}=\frac{\pi}{2}
=\frac{2}{\sqrt{a}} × \int_{0}^{\frac{\pi}{2}}a\sin^{2}{\theta}\sqrt{a-a\sin^{2}{\theta}}\left(2a\sin{\theta}\cos{\theta}\right){d\theta}
=4a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{3}{\theta}\cos{\theta}\sqrt{1-\sin^{2}}{d\theta}
=4a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{3}{\theta}\cos^{2}{\theta}{d\theta}
=4a^{2}\frac{\Gamma{\left(\frac{3+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{3+2+2}{2}\right)}}
=2a^{2}\frac{\Gamma{\left(2\right)}\Gamma{\left(\frac{3}{2}\right)}}{\Gamma{\frac{7}{2}}}
=2a^{2}\frac{\frac{1}{2}\sqrt{\pi}}{\frac{5}{2}.\frac{3}{2}.\frac{1}{2}\sqrt{\pi}}
=\frac{8a^{2}}{15}
(b):y^{2}\left(a+x\right)=x^{2}\left(a-x\right) [strophoid]

Solution:y^{2}\left(a+x\right)=x^{2}\left(a-x\right)
सीमा हेतु y=0 से x=0,a
अभीष्ट क्षेत्रफल=2 \int_{x=0}^{x=a} ydx
=2 \int_{0}^{a}x\sqrt{\frac{a-x}{a+x}} dx
=2 \int_{0}^{a}x\frac{a-x}{\sqrt{a^{2}-x^{2}}} dx
=2 \int_{0}^{a}\frac{ax}{\sqrt{a^{2}-x^{2}}} dx-2 \int_{0}^{a}\frac{x^{2}}{\sqrt{a^{2}-x^{2}}} dx
=-2a\int_{a}^{0}\frac{t}{t}dt+2 \int_{0}^{a}\frac{a^{2}-x^{2}-a^{2}}{\sqrt{a^{2}-x^{2}}} dx
=2a\int_{0}^{a}dt+2\int_{0}^{a}\sqrt{a^{2}-x^{2}}dx-2a^{2}\int_{0}^{a}\frac{1}{\sqrt{a^{2}-x^{2}}}dx
=2a\left[t\right]_{0}^{a}+2\left[\frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\left(\frac{x}{a}\right)\right]_{0}^{a}-2a^{2}\left[\sin^{-1}\left(\frac{x}{a}\right)\right]_{0}^{a}

=2a^{2}+2\frac{a^{2}}{2}.\frac{\pi}{2}-2a^{2}.\frac{\pi}{2}

=2a^{2}+2\frac{{\pi}{a^{2}}}{2}-2\frac{{\pi}{a^{2}}}{4}

=2a^{2}-2\frac{{\pi}a^{2}}{4}

=2a^{2}\left(1-\frac{\pi}{4}\right)

(c):a^{3}y^{2}=x^{4}\left(b+x\right)

Solution:a^{3}y^{2}=x^{4}\left(b+x\right)

y^{2}=\frac{x^{4}\left(b+x\right)}{a^{3}}

\Rightarrow y=\frac{x^{2}\sqrt{b+x}}{a^{\frac{3}{2}}}

अभीष्ट क्षेत्रफल=

2\int_{-b}^{0} ydx

=2\int_{-b}^{0}\frac{x^{2}\sqrt{b+x}}{a^{\frac{3}{2}}} …(1)
खण्डश: समाकलन करने पर:
\int{x^{2}}\sqrt{b+x} dx=x^{2}\int{\sqrt{b+x}}dx-\int{\frac{d}{dx}}\left(x^{2}\right)\int{\sqrt{b+x}} dx
=\frac{2x^{2}}{3}\left(b+x\right)^{\frac{3}{2}}-2\int{{x}\int{\left(b+x\right)^{\frac{1}{2}}}dx}dx+
=\frac{2}{3}x^{2}\left(b+x\right)^{\frac{3}{2}}-\frac{4}{3}x\int{\left(b+x\right)^{\frac{3}{2}}} dx+\frac{4}{3}\int{\left[\frac{d}{dx}\left(x\right)\int\left(b+x\right)^{\frac{3}{2}}dx\right]} dx
=\frac{2}{3}x^{2}\left(b+x\right)^{\frac{3}{2}}-\frac{8}{15}x\left(b+x\right)^{\frac{5}{2}}+\frac{4}{3}\int{\frac{2}{5}}\left(b+x\right)^{\frac{5}{2}}dx
=\frac{2}{3}x^{2}\left(b+x\right)^{\frac{3}{2}}-\frac{8}{15}x\left(b+x\right)^{\frac{5}{2}}+\frac{16}{105}\left(b+x\right)^{\frac{7}{2}} …(2)
समीकरण (2) से (1) में मान रखने पर:
=\frac{2}{a^{\frac{3}{2}}}[\frac{2}{3}\left[x^{2}\left(b+x\right)^{\frac{3}{2}}\right]_{-b}^{0}-\frac{8}{15}\left[x\left(b+x\right)^{\frac{5}{2}}\right]_{-b}^{0}+\frac{16}{105}\left[\left(b+x\right)^{\frac{7}{2}}\right]_{-b}^{0}]

=\frac{2}{a^{\frac{3}{2}}} × \frac{16}{105}b^{\frac{7}{2}} =\frac{32}{105}\frac{b^{\frac{7}{2}}}{a^{\frac{3}{2}}}

(d):a^{4}y^{2}=x^{4}\left(a^{2}-x^{2}\right)

Solution:a^{4}y^{2}=x^{4}\left(a^{2}-x^{2}\right)

y=\frac{x^{2}}{a^{2}}\sqrt{a^{2}-x^{2}}

अभीष्ट क्षेत्रफल=

2 ×\int_{0}^{a} ydx

सीमा हेतु y=0 से x=0,a
2 \int_{0}^{a}\frac{x^{2}}{a^{2}}\sqrt{a^{2}-x^{2}}dx
\text{ Put }x=a\sin{\theta}
\Rightarrow dx=a\cos{\theta}{d\theta}
\text{ जब } x=0 \text{ तो }{\theta}=0
\text{ जब } x=a \text{ तो }{\theta}=\frac{\pi}{2}
=2\int_{0}^{\frac{\pi}{2}}\frac{\left(a^{2}\sin^{2}{\theta}\right)}{a^{2}}\sqrt{\left(a^{2}-a^{2}\sin^{2}{\theta}\right)}\left(a\cos{\theta}{d\theta}\right)
=2a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{2}{\theta}\sqrt{1-\sin^{2}{\theta}}\cos{\theta}{d\theta}
=2a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{2}{\theta}\cos^{2}{d\theta}
=2a^{2}\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{2+2+2}{2}\right)}}
=a^{2}\frac{\Gamma{\left(\frac{3}{3}\right)}\Gamma{\left(\frac{3}{2}\right)}}{\Gamma{\left(\frac{6}{2}\right)}}
=a^{2}\frac{\frac{1}{2}\sqrt{\pi}\frac{1}{2}\sqrt{\pi}}{2}
=\frac{{\pi}a^{2}}{8}
(e):3ay^{2}=x\left(x-a\right)^{2}
Solution:3ay^{2}=x\left(x-a\right)^{2}
y=\sqrt{\frac {x}{3a}}\left(x-a\right)
अभीष्ट क्षेत्रफल=2\int_{0}^{a} ydx
=2\int_{0}^{a}\sqrt{\frac {x}{3a}}\left(x-a\right)
=\frac{2}{\sqrt{\left(3a\right)}}\int_{0}^{a}\left[x^{\frac{3}{2}}-ax^{\frac{1}{2}}\right]dx
=\frac{2}{\sqrt{\left(3a\right)}}\int_{0}^{a}\left[\frac{2}{5}x^{\frac{5}{2}}-\frac{2}{3}ax^{\frac{3}{2}}\right]_{0}^{a}

=\frac{8a^{2}}{15\sqrt{3}}

उपर्युक्त उदाहरणों के द्वारा समतल वक्रों द्वारा परिबद्ध क्षेत्रफल (Area Bounded by Plane Curves),समतल वक्रों द्वारा परिबद्ध क्षेत्रकलन (Quadrature Bounded by Plane Curves) को समझ सकते हैं।

Also Read This Article:Surface Area of Solid of Revolution

3.समतल वक्रों द्वारा परिबद्ध क्षेत्रफल (Area Bounded by Plane Curves),समतल वक्रों द्वारा परिबद्ध क्षेत्रकलन (Quadrature Bounded by Plane Curves) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:

उपर्युक्त प्रश्नों के उत्तर द्वारा समतल वक्रों द्वारा परिबद्ध क्षेत्रफल (Area Bounded by Plane Curves),समतल वक्रों द्वारा परिबद्ध क्षेत्रकलन (Quadrature Bounded by Plane Curves) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

Area Bounded by Plane Curves

समतल वक्रों द्वारा परिबद्ध क्षेत्रफल
(Area Bounded by Plane Curves)

Area Bounded by Plane Curves

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here