Area Between Two Curves in Class 12
1.कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves in Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves):
कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves in Class 12) के इस आर्टिकल में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल पर आधारित सवालों को समाकलन विधि से ज्ञात करना सीखेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Area Between Two Curves Class 12
2.कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल के उदाहरण (Area Between Two Curves in Class 12 Examples):
Example:1.दिए हुए वक्रों एवं रेखाओं से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए:
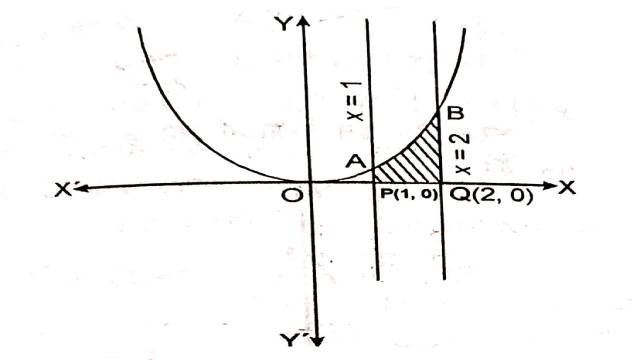
Example:1(i) y=x^2; x=1, x=2 एवं x-अक्ष
Solution:वक्रों y=x^2; x=1 तथा x=2 व x-अक्ष से घिरा हुआ क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
y=x^2 \cdots(1)
x=1 ….. (2)
x=2 …… (3)
(1) व (2) के प्रतिच्छेद बिन्दु के निर्देशांक A(1,1)
(1) व (3) के प्रतिच्छेद बिन्दु के निर्देशांक B(2,4)
अभीष्ट क्षेत्रफल=क्षेत्र PQBAP का क्षेत्रफल
=\int_1^2 y d x \\ =\int_1^2 x^2 d x \\ =\frac{1}{3}\left[x^3\right]_1^2=\frac{1}{3}\left(2^3-1^3\right) \\ =\frac{1}{3}(8-1)=\frac{7}{3} वर्ग इकाई
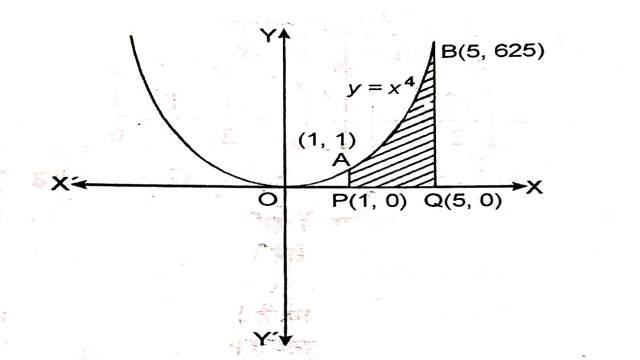
Example:1(ii). y=x^4;x=1,x=5 एवं x-अक्ष
Solution:वक्रों y=x^4 ;x=1,x=5 एवं x-अक्ष द्वारा घिरा क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
y=x^4 \cdots(1)
x=1 ….. (2)
x=5 ……. (3)
(1) व (2) के प्रतिच्छेद बिन्दु के निर्देशांक A(1,1)
(1) व (3) के प्रतिच्छेद बिन्दु के निर्देशांक B(5,625)
अभीष्ट क्षेत्रफल=क्षेत्र APQBA का क्षेत्रफल
=\int_1^5 y d x \\ =\int_1^5 x^4 d x=\frac{1}{5}\left[x^5\right]_1^5 \\ =\frac{1}{5}[3125-1]=\frac{3124}{5} \\ =624.8 वर्ग इकाई
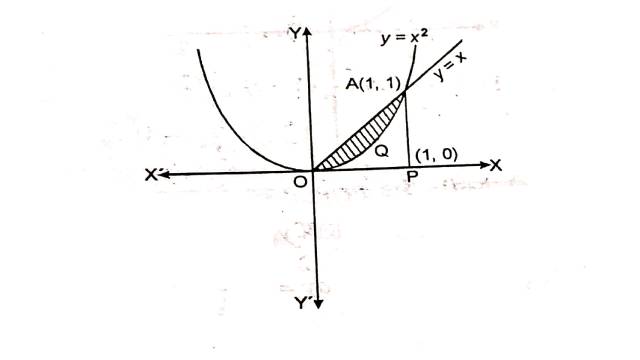
Example:2.वक्रों y=x एवं y=x^2 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:y=x एवं y=x^2 के मध्यवर्ती भाग को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है।
y=x ….. (1)
y=x^2 \cdots(2)
समीकरण (1) व (2) से:
x^2=x \\ \Rightarrow x^2-x=0 \Rightarrow x(x-1)=0 \\ x=0,1
जब x=0 तो (1) से y=0
जब x=1 तो (1) से y=1
अतः (1) व (2) से प्रतिच्छेद बिन्दु के निर्देशांक O(0,0),A(1,1)
=\int_0^1 y dx (सरल रेखा से)- \int_0^1 y dx (परवलय से)
=\int_0^1 x d x-\int_0^1 x^2 d x \\ =\frac{1}{2}\left[x^2\right]_0^1-\frac{1}{3}\left[x^3\right]_0^1 \\ =\frac{1}{2}\left(1^2-0^2\right)-\frac{1}{3}\left(1^3-0^3\right) \\ =\frac{1}{2}-\frac{1}{3}=\frac{3-2}{6}=\frac{1}{6} वर्ग इकाई
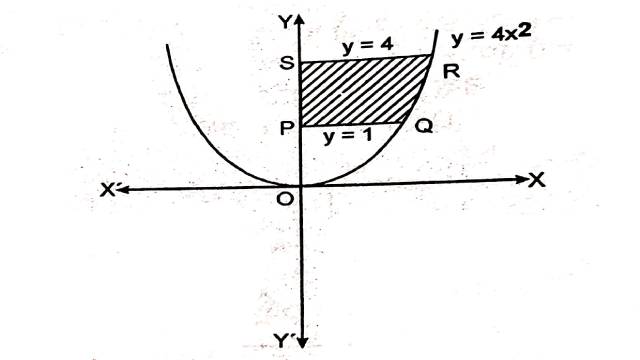
Example:3.प्रथम चतुर्थांश में सम्मिलित एवं y=4 x^2,x=0,y=1 तथा y=4 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:वक्रों y=4 x^2,x=0,y=1 तथा y=4 से घिरा हुआ क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है।
y=4 x^2 \cdots(1)
y=1 ….. (2)
y=4 …… (3)
(1) व (2) के प्रतिच्छेद बिन्दु के निर्देशांक \left(\frac{1}{2}, 1\right) तथा \left(-\frac{1}{2}, 1\right)
(1) व (3) के प्रतिच्छेद बिन्दु के निर्देशांक (1,4) व (-1,4)
अतः अभीष्ट क्षेत्रफल=क्षेत्र PQRSP का क्षेत्रफल
=\int_1^4 x d y=\int_1^4 \frac{y^{\frac{1}{2}}}{2} d y \\ =\frac{1}{2} \times \frac{2}{3}\left[y^{\frac{3}{2}}\right]_1^4 \\ =\frac{1}{3}\left[4^{\frac{3}{2}}-1\right]=\frac{7}{3} वर्ग इकाई
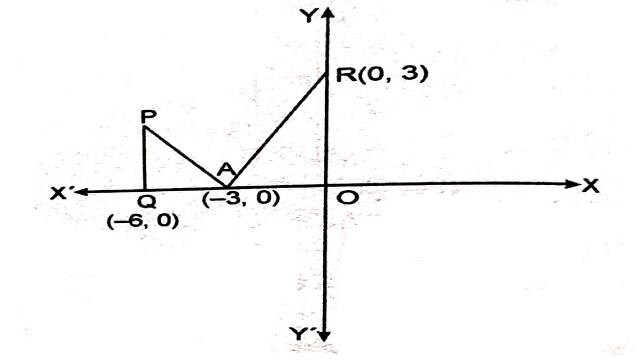
Example:4. y=|x+3| का ग्राफ खींचिए एवं \int_{-6}^0|x+3| d x का मान ज्ञात कीजिए।
Solution: y=|x+3|
y= \begin{cases}x+3 \text { जब } x \geq -3 \\ -(x+3) \text { जब } x<-3 \end{cases}
रेखाओं y=x+3 तथा y=-(x+3) को चित्र द्वारा प्रदर्शित किया गया है।दोनों का प्रतिच्छेद बिन्दु (-3,0) है।
अभीष्ट क्षेत्रफल=\int_{-6}^{-3} -(x+3) d x +\int_{-3}^0 (x+3) d x \\ =-\left[\frac{x^2}{2}+3 x\right]_{-6}^{-3}+\left[\frac{x^2}{2}+3 x\right]_{-3}^0 \\ =-\left[\frac{(-3)^2}{2}+3 \times -3-\frac{(-6)^2}{2}-3 \times -6\right] +\left[0-\frac{(-3)^2}{2}-3 \times -3\right] \\ =-\left[\frac{9}{2}-9 -18+18\right] +\left[-\frac{9}{2}+9\right] \\ =\frac{9}{2}+\frac{9}{2} \\=\frac{18}{2}=9 वर्ग इकाई
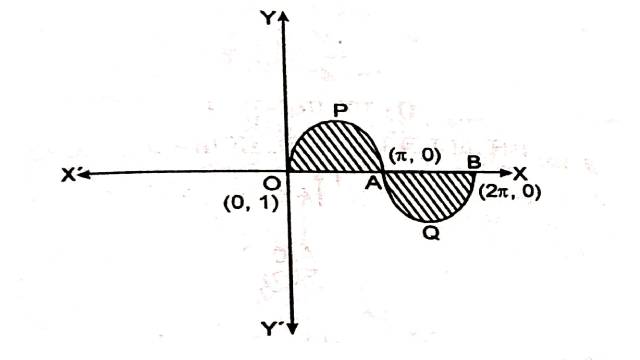
Example:5.x=0 एवं x= 2 \pi तथा y=\sin x वक्र से घिरे क्षेत्रफल ज्ञात कीजिए।
Solution:वक्र y=\sin x ,x=0 तथा x= 2 \pi से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
अभीष्ट क्षेत्रफल=क्षेत्र OPAO का क्षेत्रफल+क्षेत्र AQBA का क्षेत्रफल
=\int_0^\pi y d x+\int_0^{2 \pi}(-y) d x \\ =\int_0^\pi \sin x d x-\int_\pi^{2 \pi} \sin x d x \\ =-[\cos x]_0^\pi+[\cos x]_\pi^{2 \pi} \\ =-[\cos \pi-\cos 0]+[\cos 2 \pi-\cos \pi] \\=-(-1-1)+(1+1) \\ =2+2=4 वर्ग इकाई
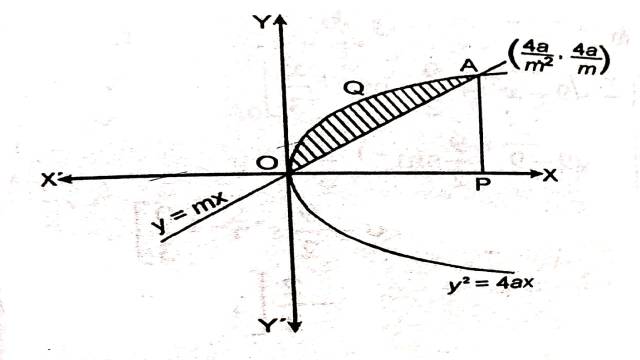
Example:6. परवलय y^2=4 a x एवं रेखा y=mx से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:- परवलय y^2=4 a x एवं रेखा y=mx से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
y^2=4 a x \cdots(1)
y=mx ….. (2)
(1) व (2) से:
(m x)^2=4ax \Rightarrow m^2 x^2-4 a x=0 \\ \Rightarrow x\left(m^2 x-4 a\right)=0 \Rightarrow x=0, x=\frac{4 a}{m}
जब x=0 तो (2) से y=0
जब x=\frac{4 a}{m^2} तो (2) से y=\frac{4 a}{m}
अतः (1) व (2) का प्रतिच्छेद बिन्दु O(0,0), A\left( \frac{4 a}{m^2} , \frac{4 a}{m}\right)
अतः अभीष्ट क्षेत्रफल=\int_0^{\frac{4a}{m^2}} y d x (परवलय से)-\int_0^{\frac{4a}{m^2}} y d x (सरल रेखा से)
=\int_0^{\frac{4a}{m^2}} \sqrt{4ax} d x-\int_0^{\frac{4a}{m^2}} (mx) dx \\ =2 \sqrt{a} \times \frac{2}{3}\left[x^{\frac{3}{2}}\right]_0^{\frac{4 a}{m^2}}-\frac{m}{2}\left[x^2\right]_0^{\frac{4 a}{m 2}} \\ =\frac{4 \sqrt{a}}{3} \cdot \frac{8 a \sqrt{a}}{m^3}-\frac{m}{2} \cdot \frac{16 a^2}{m^4} \\ =\frac{32}{3} \frac{a^2}{m^3}-\frac{8 a^2}{m^3}=\frac{8 a^2}{3 m^3} वर्ग इकाई
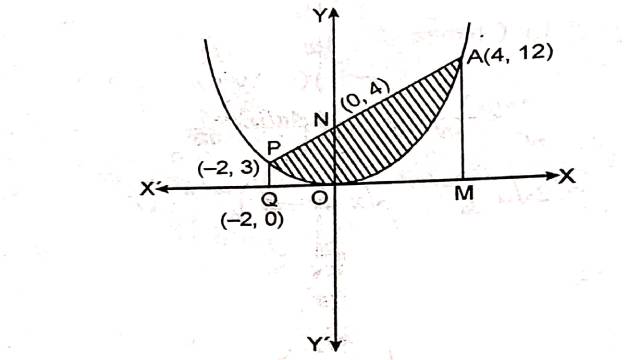
Example:7.परवलय 4 y=3 x^2 एवं रेखा 2y=3x+12 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:परवलय 4 y=3 x^2 एवं रेखा 2y=3x+12 से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है:
4 y=3 x^2 \cdots(1)
2y=3x+12 …. (2)
(1) व (2) से:
2(3 x+12)=3 x^2 \Rightarrow 3 x^2-6 x-24=0 \\ \Rightarrow x^2-2 x-8=0 \Rightarrow x^2-4 x+2 x-8=0 \\ \Rightarrow x(x-4)+2(x-4)=0 \Rightarrow(x+2)(x-4)=0 \\ \Rightarrow x=-2,4
जब x=-2 तो (2) से y=3
जब x=4 तो (2) से y=12
अतः प्रतिच्छेद बिन्दु P(-2,3),A(4,12) है।
जब x=0 तो (2) से y=6
अतः रेखा y-अक्ष को (0,6) पर काटती है।
अभीष्ट क्षेत्रफल=क्षेत्र PQMAP का क्षेत्रफल-क्षेत्र PQOMA का क्षेत्रफल
=\int_{-2}^4 y d x (सरल रेखा से)-\int_{-2}^4 y d x (परवलय से)
=\int_{-2}^{-2}\left(\frac{3 x+12}{2}\right) d x-\int_{-2}^4\left(\frac{3 x^2}{4}\right) d x \\ =\frac{1}{2}\left[\frac{3 x^2}{2}+12 x\right]_{-2}^4-\frac{3}{4}\left[\frac{x^3}{3}\right]_{-2}^4 \\ =\frac{1}{2} \left[\frac{3 \times 4^2}{2}+12 \times 4-\frac{3}{2}(-2)^2-12 x-2\right]-\frac{1}{4}\left[4^3-(-2)^3\right] \\ =\frac{1}{2}[24+48-6+24]-\frac{1}{4}[64+8] \\ =45-18=27 वर्ग इकाई
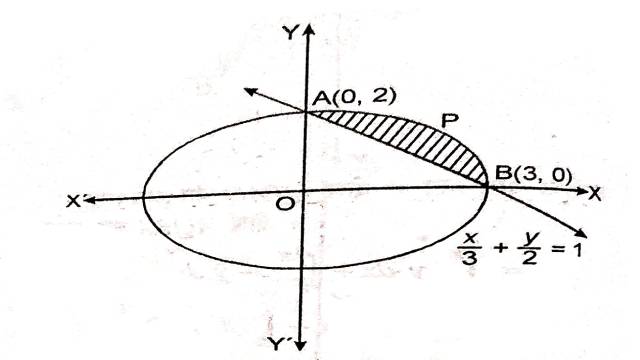
Example:8.दीर्घवृत्त \frac{x^2}{9}+\frac{y^2}{4}=1 एवं रेखा \frac{x}{3}+\frac{y}{2}=1 से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:दीर्घवृत्त \frac{x^2}{9}+\frac{y^2}{4}=1 एवं रेखा \frac{x}{3}+\frac{y}{2}=1 से घिरा हुआ लघु क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है।
\frac{x^2}{9}+\frac{y^2}{4}=1 \cdots(1) \\ \frac{x}{3}+\frac{y}{2}=1 \cdots(2)
समीकरण (1) व (2) से:
\frac{x^2}{9}+\frac{1}{4} \times 4\left(1-\frac{x}{3}\right)^2=1 \\ \Rightarrow \frac{x^2}{9}+1-\frac{2 x}{3}+\frac{x^2}{9}=1 \\ \Rightarrow 2 x^2-6 x=0 \\ \Rightarrow 2 x(x-3)=0 \Rightarrow x=3
x=0 तब y=2
अतः प्रतिच्छेद बिन्दु A(0,2),B(3,0) है।
अभीष्ट क्षेत्रफल=क्षेत्र OBPAO का क्षेत्रफल-का क्षेत्रफल
=\int_0^3 y d x (परवलय से)- \int_0^3 y d x (रेखा से)
=\int_0^3 2 \sqrt{1-\frac{x^2}{9}} d x-\int_0^3 2\left(1-\frac{x}{3}\right) d x \\ =\int^3_0 \left[\frac{\frac{x}{3} \sqrt{1-\frac{x^2}{9}}}{2}+\frac{1}{2} \sin ^{-1} \frac{x}{3}\right]_0^3-2\left[x-\frac{x^2}{6}\right]_0^3 \\ =6\left[0+\frac{1}{2} \sin ^{-1}\left(\frac{3}{3}\right)-0\right]-2\left[3-\frac{3^2}{6}-0 \right] \\ =3 \sin ^{-1}(1)-2 \times\left[3-\frac{3}{2}\right] \\ =\frac{3 \pi}{2}-3=\frac{3}{2}(\pi-2) वर्ग इकाई
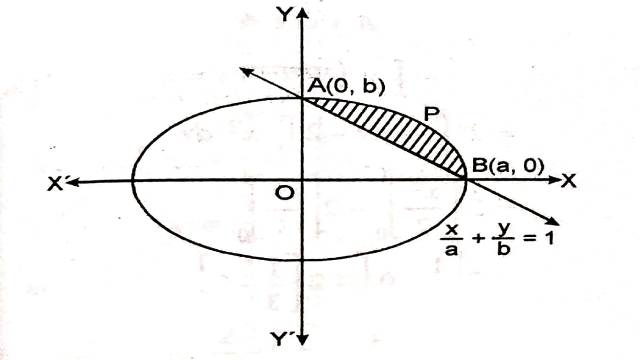
Example:9. दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 एवं रेखा \frac{x}{a}+\frac{y}{b}=1 से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution: दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 एवं रेखा \frac{x}{a}+\frac{y}{b}=1 से घिरा लघु क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \cdots(1) \\ \frac{x}{a}+\frac{y}{b}=1 \cdots(2)
(1) व (2) से:
\frac{x^2}{a^2}+\frac{b^2}{b^2}\left(1-\frac{x}{a}\right)^2=1 \\ \Rightarrow \frac{x^2}{a^2}+1-\frac{2 x}{a}+\frac{x^2}{a^2}=1 \\ \Rightarrow \frac{2 x^2}{a^2}-\frac{2 x}{a}=0 \\ \Rightarrow \frac{2 x}{a} \left(\frac{x-1}{a}\right)=0 \\ \Rightarrow x=0, x=a
जब x=0 तो y=b
जब x=a तो y=0
अतः परवलय व रेखा का प्रतिच्छेद बिन्दु A(0,b),B(a,0)
अभीष्ट क्षेत्रफल=क्षेत्र ABPA का क्षेत्रफल
=क्षेत्र OAPBO का क्षेत्रफल-का क्षेत्रफल
=\int_0^a y d x (दीर्घवृत्त से)-\int_0^a y d x (रेखा से)
=b \int_0^a \sqrt{1-\frac{x^2}{a^2}} d x-b \int_0^a\left(1-\frac{x}{a}\right) d x \\ =a b\left[\frac{\frac{x}{a} \sqrt{1-\frac{x^2}{a}}}{2}+\frac{1}{2} \sin ^{-1}\left(\frac{x}{a}\right)\right]_0^a-b\left[x-\frac{x^2}{2 a}\right]_0^a \\ =a b\left[0+\frac{1}{2} \sin ^{-1}\left(\frac{a}{a}\right)-0\right]-b\left[a-\frac{a^2}{2 a}-0\right] \\ =\frac{a b}{2} \sin ^{-1}(1)-a b+\frac{a b}{2} \\ =\frac{a b}{2} \cdot \frac{\pi}{2}-\frac{a b}{2} \\ =\frac{a b}{4}(\pi-2) वर्ग इकाई
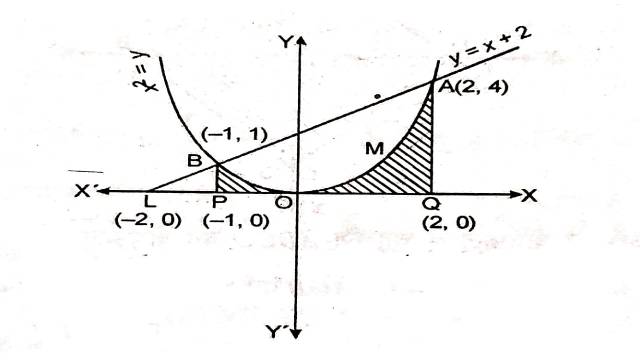
Example:10. परवलय x^2=y ,रेखा y=x+2 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय x^2=y ,रेखा y=x+2 एवं x-अक्ष से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है।
x^2=y \cdots(1)
y=x+2 … (2)
(1) व (2) से:
x^2 =x+2 \Rightarrow x^2-x-2=0 \\ \Rightarrow(x+1)(x-2)=0 \Rightarrow x=-1,2
जब x=-1 तो (2) से y=1
जब x=2 तो (2) से y=4
अतः प्रतिच्छेद बिन्दु B(-1,1),A(2,4) है।
जब x=0 तो y=0 तथा जब y=0 तो x=-2
अतः अक्षों को रेखा (-2,0) व (0,2) पर काटती है।
अभीष्ट क्षेत्रफल=क्षेत्र BPOQAMB का क्षेत्रफल
=क्षेत्र POQABP का क्षेत्रफल-क्षेत्र BQMAB का क्षेत्रफल
=\int_{-1}^2 y d x (सरल रेखा से)- \int_{-1}^2 y d x (परवलय से)
=\int_{-1}^2(x+2) d x-\int_{-1}^2 x^2 d x \\ =\left[\frac{x^2}{2}+2 x\right]^2_{-1}-\left[\frac{x^3}{3} \right]_{-1}^2 \\ =\frac{(2)^2}{2}+2 \times 2-\frac{(-1)^2}{2}-2 \times -1-\left(\frac{2^3}{3}-\frac{(-1)^3}{3}\right) \\ =2+4-\frac{1}{2}+2-\left(\frac{8}{3}+\frac{1}{3}\right) \\ =\frac{15}{2}-3 \\ =\frac{9}{2} वर्ग इकाई
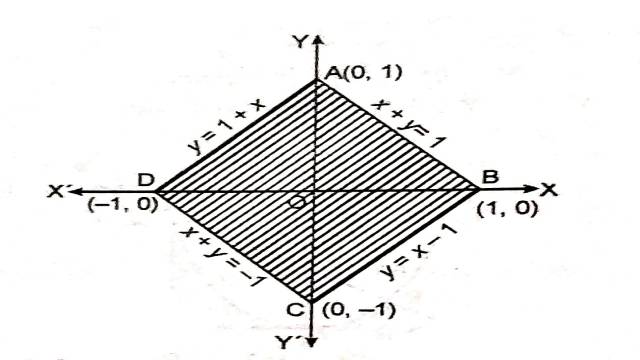
Example:11.समाकलन विधि का उपयोग करते हुए वक्र |x|+|y|=1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution: |x|+|y|=1 से बनी रेखाओं से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है।
(1.) |x|+|y|=1 से जब x>0,y>0 \Rightarrow x+y=1
(2.) |x|+|y|=1से जब x<0,y>0 \Rightarrow -x+y=1
(3.) |x|+|y|=1 से जब x<0,y<0 \Rightarrow -x-y=1
(4.) |x|+|y|=1 से जब x>0,y<0 \Rightarrow x-y=1
अभीष्ट क्षेत्रफल=चतुर्भुज ABCD का क्षेत्रफल
=4× \triangle AOB का क्षेत्रफल
=4 \int_0^1(1-x) d x=4\left[x-\frac{x^2}{2}\right]_0^1 \\ =4 (1-\frac{1^2}{2})=4 \times \frac{1}{2}=2 वर्ग इकाई
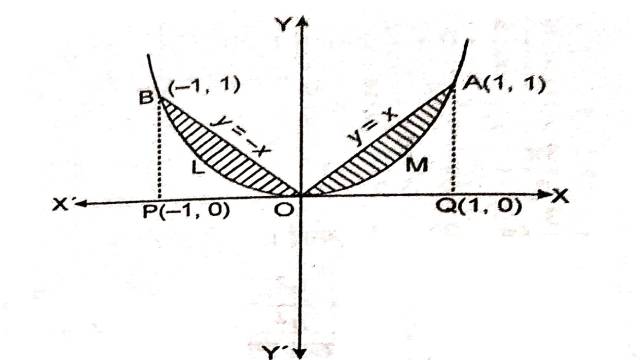
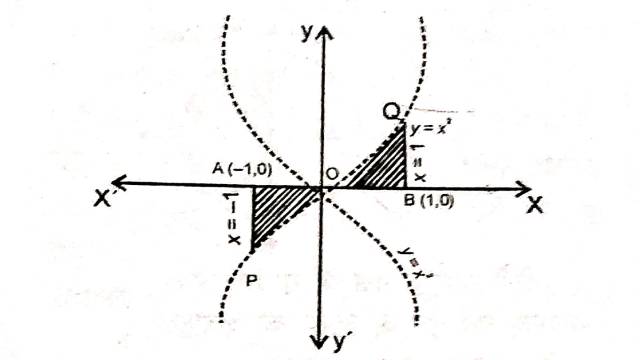
Example:12.वक्रों \left\{(x, y): y \geq x^2 \text { तथा } y=|x| \right\} से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:परवलय y=x^2 तथा y=|x| से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
y=x^2 \cdots(1)
y=x …. (2)
y=-x ….. (3)
(1) व (2) से:
x^2-x \Rightarrow x^2-x=0 \\ \Rightarrow x(x-1)=0 \Rightarrow x=0, 1
जब x=0 तो (2) से y=0
जब x=1 तो (2) से y=1
अतः (1) व (2) का प्रतिच्छेद बिन्दु O(0,0) व A(1,1)
(1) व (3) से:
B(-1,1) व O(0,0)
(2) व (3) से:O(0,0)
अभीष्ट क्षेत्रफल=क्षेत्र BLOMA का क्षेत्रफल
=2× \triangle OMA का क्षेत्रफल
=2 × [\triangle OQA का क्षेत्रफल-क्षेत्र OMAQO का क्षेत्रफल]
=2 \int_0^1 y d x (सरल रेखा से)- 2 \int_0^1 y d x (परवलय से)
=2 \int_0^1 x d x-2 \int_0^1 x^2 d x \\ =2\left[\frac{x^2}{2}\right]_0^1-2\left[\frac{x^3}{3} \right]_0^1 \\ =1-2 \times \frac{1}{3}=\frac{1}{3} वर्ग इकाई
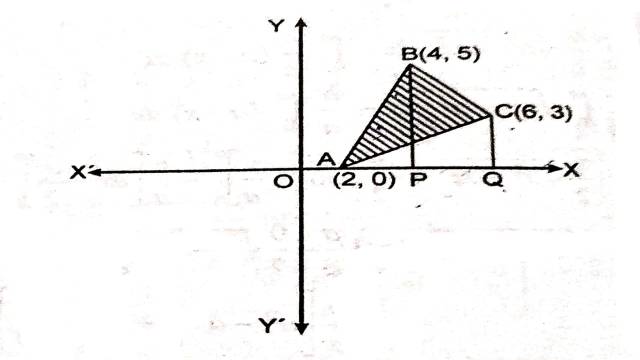
Example:13.समाकलन विधि का उपयोग करते हुए एक ऐसे त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए जिसके शीर्षों के निर्देशांक A(2,0),B(4,5) एवं C(6,3) हैं।
Solution:A(2,0),B(4,5) से गुजरने वाली रेखा का समीकरण:
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)\\ y-0=\frac{5-0}{4-2}(x-2) \\ \Rightarrow y=\frac{5}{2}(x-2)
बिन्दु B(4,5) व C(6,3) से गुजरने वाली रेखा का समीकरण:
\Rightarrow y-5=\frac{3-5}{6-4}(x-4) \\ \Rightarrow y-5=-x+4 \\ \Rightarrow y=-x+9 \cdots(2)
बिन्दु A(2,0) व C(6,3) से गुजरने वाली रेखा का समीकरण:
y-0=\frac{3-0}{6-2}(x-2) \\ \Rightarrow y=\frac{3}{4}(x-2) \cdots(3)
\triangle ABC का क्षेत्रफल=\triangle ABP का क्षेत्रफल+समलम्ब चतुर्भुज BPQC का क्षेत्रफल- \triangle AQC का क्षेत्रफल
=\int_2^4 y d x [समीकरण (1) से]+ \int_4^6 y d x [समीकरण (2) से]-\int_2^6 y d x [समीकरण (3) से]
=\int_2^4 \frac{5}{2}(x-2) d x+\int_4^6(-x+9) d x-\int_2^6 \frac{3}{4}(x-2) d x \\ =\frac{5}{2}\left[\frac{x^2}{2}-2 x\right]_2^4+\left[-\frac{x^2}{2}+9 x\right]_4^6-\frac{3}{4}\left[\frac{x^2}{2}-2 x\right]_2^6 \\ =\frac{5}{2}\left[\frac{16}{2}-2 \times 4-\frac{2^2}{2}+2 \times 2\right]+\left[-\frac{6^2}{2}+9 \times 6+\frac{4^2}{2}-9 \times 4\right] -\frac{3}{4}\left[\frac{6^2}{2}-2 \times 6-\frac{(2)^2}{2}+2 \times 2\right] \\ =\frac{5}{2}[8-8-2+4]+[-18+54+8-36] -\frac{3}{4}[18-12-2+4] \\=5+8-\frac{3}{4} \times 8=7 वर्ग इकाई
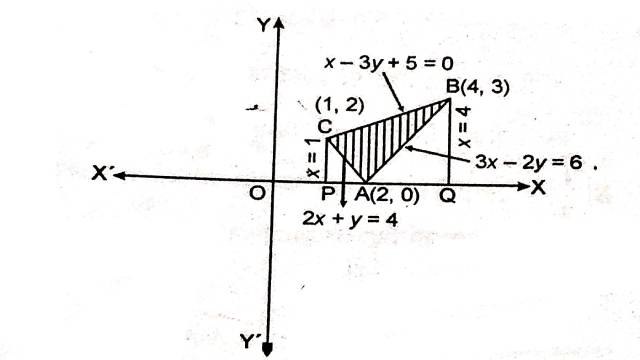
Example:14.समाकलन विधि का उपयोग करते हुए रेखाओं 2x+y=4,3x-2y=6 एवं x-3y+5=0 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:रेखाओं 2x+y=4,3x-2y=6 तथा x-3y+5=0 से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है:
2 x+y=4 \Rightarrow y=4-2 x \cdots(1) \\ 3 x-2 y=6 \Rightarrow y=\frac{1}{2}(3 x-6) \cdots(2) \\ x-3 y+5=0 \Rightarrow y=\frac{1}{3}(x+5) \cdots(3)
(1) व (2) का प्रतिच्छेद बिन्दु A(2,0)
(2) व (3) का प्रतिच्छेद बिन्दु B(4,3)
(1) व (3) का प्रतिच्छेद बिन्दु C(1,2)
अभीष्ट क्षेत्रफल=\triangle ABC का क्षेत्रफल
=समलम्ब चतुर्भुज PQBC का क्षेत्रफल- \triangle PAC का क्षेत्रफल- \triangle ABQ का क्षेत्रफल
=\int_1^4 ydx (समीकरण (3) से)- \int_1^2 y dx(समीकरण (1) से)- \int_2^4 y dx(समीकरण (2) से)
=\int_1^4 \frac{1}{3}(x+5) d x-\int_1^2(4-2 x) d x-\int_2^4 \frac{1}{2}(3 x-6) d x\\ =\frac{1}{3} \left[\frac{x^2}{2}+5 x\right]_1^4-\left[4 x-x^2\right]_1^2-\frac{1}{2}\left[\frac{3 x^2}{2}-6 x\right]_{2}^4 \\=\frac{1}{3}\left[\frac{4^2}{2}+5 \times 4-\frac{1^2}{2}-5 \times 1\right]-\left[4 \times 2+2^2-4 \times 1+1^2\right] -\frac{1}{2}\left[\frac{3}{2} \times 4^2-6 \times 4-\frac{3}{2} \times 2^2+6 \times 2\right] \\=\frac{1}{3}\left[8+20-\frac{1}{2}-5\right]-[8-4-4+1]-\frac{1}{2}[24-24-6+12]\\=\frac{1}{3} \times \frac{45}{2}-1-\frac{1}{2} \times 6=\frac{7}{2} वर्ग इकाई
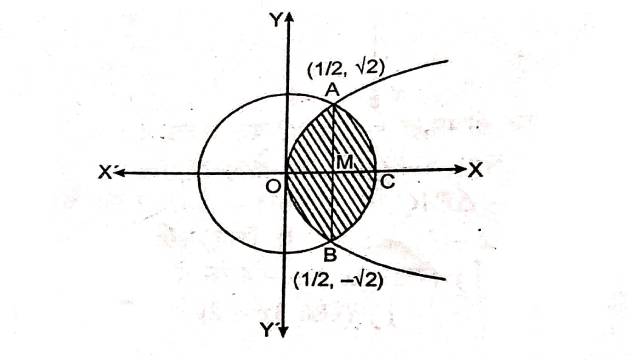
Example:15. क्षेत्र \{ (x,y); y^2 \le 4x,4x^2+4y^2 \le 9\} का क्षेत्रफल ज्ञात कीजिए।
Solution:परवलय y^2 \leq 4 तथा x^2+y^2 \leq \frac{9}{4} वृत्त के घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
y^2=4 x \cdots(1)\\ x^2+y^2=\frac{9}{4} \cdots(2)
(1) व (2) से:
x^2+4 x=\frac{9}{4} \\ \Rightarrow x^2+16 x-9=0 \\ \Rightarrow 4 x^2+18 x-2 x-9=0 \\ \Rightarrow 2 x(2 x+9)-1(2 x+9)=0 \\ \Rightarrow(2 x-1)(2 x+9)=0 \\ \Rightarrow x=\frac{1}{2}, x=-\frac{9}{2} (असम्भव है)
y= \pm \sqrt{2} [(1) से]
अभीष्ट क्षेत्रफल=2×क्षेत्र AOCA का क्षेत्रफल
=2×[क्षेत्र OMAO का क्षेत्रफल+क्षेत्र MCAM का क्षेत्रफल]
=2 \int_0^{\frac{1}{2}} y d x (परवलय से)+ \int_{\frac{1}{2}}^{\frac{3}{2}} y d x (वृत्त से)
=2 \int_0^{\frac{1}{2}} \sqrt{4 x} d x+2 \int_{\frac{1}{2}}^{\frac{3}{2}} \frac{\frac{1}{2}}{\sqrt{\frac{9}{4}-x^2}} d x \\ =4\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^{\frac{1}{2}}+2\left[\frac{x \sqrt{\frac{9}{4}-x^2}}{2}+\frac{9}{8} \sin ^{-1} \frac{x}{\frac{3}{2}} \right]_{\frac{1}{2}}^{\frac{3}{2}} \\ =4 \times \frac{2}{3}\left[\frac{1}{2 \sqrt{2}}-0\right]+\frac{3}{2} \sqrt{\frac{9}{4}-\frac{9}{4}}+\frac{9}{4} \sin ^{-1} \frac{\frac{3}{2}}{\frac{3}{2}} -\frac{1}{2} \sqrt{\frac{9}{4}-\frac{1}{4}}-\frac{9}{4} \sin ^{-1}\left(\frac{\frac{1}{2}}{\frac{3}{2}}\right) \\ =\frac{4}{3 \sqrt{2}}+\frac{9}{4} \sin ^{-1}(1)-\frac{\sqrt{2}}{2}-\frac{9}{4} \sin ^{-1}\left(\frac{1}{3}\right) \\=\frac{8-2}{3 \sqrt{2}}+\frac{9}{4} \cdot \frac{\pi}{2}-\frac{9}{4} \sin ^{-1} \left(\frac{1}{3}\right) \\ =\frac{6}{3 \sqrt{2}}+\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1}\left(\frac{1}{3}\right) वर्ग इकाई
16 से 20 तक प्रश्नों के सही उत्तर का चयन कीजिए:
Example:16.वक्र y=x^3 , x-अक्ष एवं कोटियों x=-2,x=1 से घिरे क्षेत्र का क्षेत्रफल है:
(A) -9 (B)-\frac{15}{4} (C)\frac{15}{4} (D)\frac{17}{4}
Solution: y=x^3,x-अक्ष एवं कोटियों x=-2,x=1 से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है:
y=x^3 \cdots(1)
x=-2 …. (2)
x=1 …… (3)
(1) व (2) से:y=-8,x=-2
(1) व (3) से:y=1,x=1
अतः प्रतिच्छेद बिन्दु के निर्देशांक B(1,1),A(-2,-8)
अभीष्ट क्षेत्रफल=\left|\int_{-2}^0 y d x\right|+\left|\int_0^1 y d x\right| \\=\left|\int_{-2}^0 x^3 d x\right|+\left|\int_0^1 x^3 d x\right| \\ =\left| \left[\frac{x^4}{4}\right]_{-2}^0\right|+\left|\left[\frac{x^4}{4}\right]_0^1\right| \\ =\left|-\frac{(-2)^4}{4}\right|+\left|\frac{1^4}{4}\right|=4+\frac{1}{4}=\frac{17}{4} वर्ग इकाई
अतः विकल्प (D) सही है।
Example:17.वक्र y=x|x| ;x-अक्ष एवं कोटियों x=-1 तथा x=1 से घिरे क्षेत्र का क्षेत्रफल है:
(A)0 (B)\frac{1}{3} (C)\frac{2}{3} (D)\frac{4}{3}
Solution: y=x|x|
y=x^2 जब x>0 तथा y=-x^2 जब x<0
अतः y=x^2, y=-x^2 ,x-अक्ष एवं कोटियों x=-1 तथा x=1 से घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल ज्ञात करना है।
y=x^2 \cdots(1)
x=1 … (2)
y=-x^2 \cdots(3)
x=-1 …. (4)
(1) व (2) से:y=1,x=1
(3) व (4) से y=-1,x=-1
अतः प्रतिच्छेद बिन्दु (1,1),(-1,-1)
अभीष्ट क्षेत्रफल=\left|\int_{-1}^0 y d x\right| [समीकरण (3) से]+ \left|\int_{0}^1 y d x\right| [ समीकरण (1) से]
=\left|\int_{-1}^0-x^2 d x \right| +\left| \int_0^1 x^2 dx \right| \\ =\left|\left[-\frac{x^3}{3} \right]_{-1}^0 \right|+\left|\left[\frac{x^3}{3}\right]_0^1\right| \\=\frac{1^3}{3}+\frac{1^3}{3}=\frac{2}{3} वर्ग इकाई
अतः विकल्प (C) सही है।
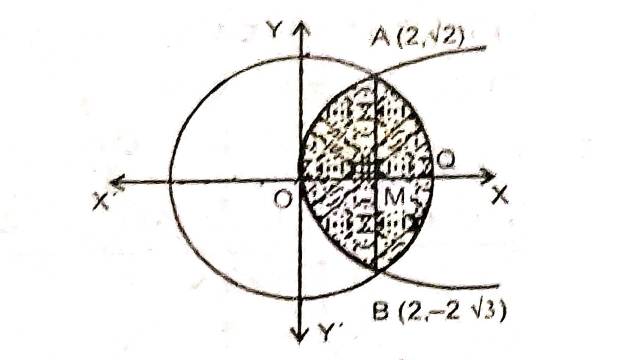
Example:18.क्षेत्र y^2 \geq 6 x और x^2+y^2=16 वृत्त में सम्मिलित क्षेत्र का क्षेत्रफल है:
(A) \frac{4}{3}(4 \pi-\sqrt{3}) (B) \frac{4}{3}(4 \pi+\sqrt{3}) (C) \frac{4}{3}(8 \pi-\sqrt{3}) (D) \frac{4}{3}(8 \pi+\sqrt{3})
Solution:परवलय तथा वृत्त द्वारा जो छायांकित भाग दर्शाया गया है उसके बाहर का क्षेत्र ज्ञात करना है:
y^2=6x \cdots(1) \\ x^2+y^2=16 \cdots(2)
(1) व (2) से:
\Rightarrow x^2+6 x=16 \\ \Rightarrow x^2+6 x-16=0 \\ \Rightarrow x^2+8 x-2 x-16=0 \\ \Rightarrow x(x+8)-2(x+8)=0 \\ \Rightarrow (x-2)(x+8)=0 \\ \Rightarrow x=2,-8 ( असम्भव है)
अतः जब x=2,तो (1) से y= \pm \sqrt{12}= \pm 2 \sqrt{3}
फलतः वृत्त व परवलय का प्रतिच्छेद बिन्दु A(2,2 \sqrt{3}) B(2,-2 \sqrt{3})
अभीष्ट क्षेत्रफल=2 \int_{-4}^2 y dx (वृत्त से)-2 \int_0^2 y d x (परवलय से)
=2 \int_{-4}^2 \sqrt{16-x^2} d x-2 \int_0^2 \sqrt{6 x} d x \\ =2\left[\frac{x \sqrt{16-x^2}}{2}+\frac{16}{2} \sin ^{-1}\left(\frac{x}{4}\right)\right]_{-4}^2-2 \sqrt{6}\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]^2 \\ =2\left[\sqrt{12}+8 \sin ^{-1}\left(\frac{2}{4}\right)-8 \sin ^{-1}\left(\frac{-4}{4}\right) \right]-2 \sqrt{6} \times \frac{2}{3}\left(2^{\frac{3}{2}}\right) \\ =2 \sqrt{12}+8 \sin ^{-1}\left(\frac{1}{2}\right)+8 \sin ^{-1}(1)-\frac{4 \sqrt{6}}{3} \times 2 \sqrt{2} \\ =2 \sqrt{12}+16 \times \frac{\pi}{6}+16 \times \frac{\pi}{2}-\frac{8 \sqrt{12}}{3} \\ =4 \sqrt{3}-\frac{16 \sqrt{3}}{3}+\frac{8 \pi}{3}+8 \pi \\ =\frac{12 \sqrt{3}-16 \sqrt{3}}{3}+\frac{8 \pi+24 \pi}{3} \\ =\frac{32 \pi}{3}-\frac{4 \sqrt{3}}{3} \\ =\frac{4}{3}(8 \pi-\sqrt{3}) वर्ग इकाई
अतः विकल्प (C) सही है।
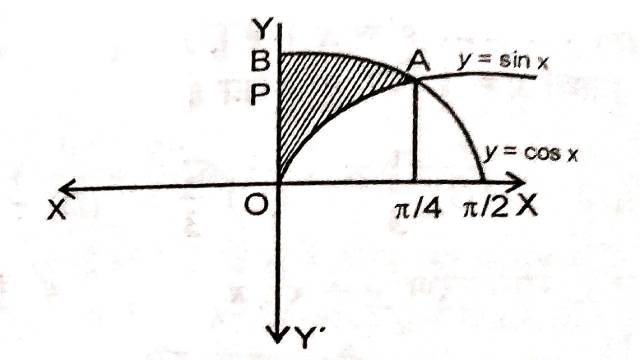
Example:19.y-अक्ष , y=\cos x एवं y=\sin x , 0 \leq x \leq \frac{\pi}{2} से घिरे क्षेत्र का क्षेत्रफल है:
(A) 2(\sqrt{2}-1) (B) \sqrt{2}-1 (C)\sqrt{2}+1 (D)\sqrt{2}
Solution:y-अक्ष , y=\cos x तथा y=\sin x द्वारा घिरे क्षेत्र को चित्र में छायांकित भाग द्वारा दर्शाया गया है:
y=\cos x \cdots(1) \\ y=\sin x \cdots(2)
(1) व (2) से:
\sin x=\cos x \\ \Rightarrow x=\frac{\pi}{4}
(1) से y=\frac{1}{\sqrt{2}}
अतः प्रतिच्छेद बिन्दु A\left(\frac{\pi}{4}, \frac{1}{\sqrt{2}}\right) है।
अभीष्ट क्षेत्रफल=क्षेत्र OABO का क्षेत्रफल
=\int_0^{\frac{\pi}{4}} y d x(y=\cos x \text{ से } )-\int_0^{\frac{\pi}{4}} y d x\left(y=\sin x \text{ से } \right) \\ =\int_0^{\frac{\pi}{4}} \cos x d x-\int_0^{\frac{\pi}{4}} \sin x d x \\ =[\sin x]_0^{\frac{\pi}{4}}+[\cos x]_0^{\frac{\pi}{4}} \\ =\sin \frac{\pi}{4}-0+\cos \frac{\pi}{4}-\cos 0 \\ =\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-1=(\sqrt{2}-1) वर्ग इकाई
अतः विकल्प (B) सही है।
उपर्युक्त उदाहरणों के द्वारा कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves in Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) को समझ सकते हैं।
3.कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल पर आधारित समस्याएँ (Problems Based on Area Between Two Curves in Class 12):
(1.)वक्र y=|x+1| तथा कोटि x=-3 एवं x=1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
(2.)वक्र y=2 \sqrt{1-x^2} तथा x-अक्ष के परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
उत्तर (Answers):(1.)4 वर्ग इकाई (2.) \pi वर्ग इकाई
उपर्युक्त सवालों को हल करने पर कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves in Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) को ठीक से समझ सकते हैं।
Also Read This Article:- Area Under Simple Curves by Integral
4.कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Frequently Asked Questions Related to Area Between Two Curves in Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.उर्ध्वाधर पट्टियों के अनुसार क्षेत्रफल ज्ञात करने का सूत्र लिखो। (Write the Formula for Finding the Area According to the Vertical Strips):
उत्तर:वक्र y=f(x),x-अक्ष एवं रेखाओं x=a तथा x=b (b>a) से घिरे क्षेत्र के क्षेत्रफल का सूत्र:
क्षेत्रफल= \int_a^b y d x=\int_a^b f(x) d x है।
प्रश्न:2.क्षैतिज पट्टियों के अनुसार क्षेत्रफल ज्ञात करने का सूत्र लिखो। (Write the Formula for Finding the Area According to the Horizontal Strips):
उत्तर:वक्र x=\phi(y) ,y-अक्ष एवं रेखाओं y=c,y=d से घिरे क्षेत्र का क्षेत्रफल का सूत्र:
क्षेत्रफल=\int_C^d x dy=\int_c^d \phi(y) dy है।
प्रश्न:3.जेम्स बी. ब्रिस्टल के अनुसार एक अच्छा गणित का छात्र किस तरह अध्ययन करता है? (HOW DOES A GOOD MATH STUDENT STUDY ACCORDING TO JAMES B. BRISTOL?):
उत्तर:जैसे एक पर्वतारोही पहाड़ पर चढ़ता है, वैसे ही गणित का एक अच्छा छात्र नई सामग्री का अध्ययन करता है क्योंकि वह वहां है। -जेम्स बी. ब्रिस्टल
(Just as a mountaineer climbs a mountain-bacause it is there,so a good mathematics student studies new material because it is there. -JAMES B. BRISTOL)
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves in Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Area Between Two Curves in Class 12
कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल
(Area Between Two Curves in Class 12)
Area Between Two Curves in Class 12
कक्षा 12 में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves in Class 12)
के इस आर्टिकल में दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल पर आधारित सवालों को समाकलन
विधि से ज्ञात करना सीखेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.