Angle Subtended by Arc of Circle 9th
1.एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Angle Subtended by Arc of Circle 9th),कक्षा 9 में एक वृत्त के चाप द्वारा अंतरित कोण (Angle Subtended by Arc of Circle in Class 9):
एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Angle Subtended by Arc of Circle 9th) के इस आर्टिकल में वृत्त,जीवा द्वारा एक बिन्दु पर अन्तरित कोण,तीन बिन्दुओं से जाने वाला वृत्त,समान जीवाएँ और उनकी केन्द्र से दूरियाँ,एक चाप द्वारा अंतरित कोण तथा चक्रीय चतुर्भुज पर आधारित सवालों को हल करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Equal Chords and Distances From Centre
2.एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 के साधित उदाहरण (Angle Subtended by Arc of Circle 9th Solved Examples):
Example:1.सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों की केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण अन्तरित करती है।
Solution:दिया है (Given):दो वृत्त जिनके केन्द्र A और B हैं,परस्पर C और D पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove): \angle ACB=\angle ADB
उपपत्ति (Proof): \triangle ACB तथा \triangle ADB में
AC=AD (एक ही वृत्त की त्रिज्याएँ)
BC=BD (एक ही वृत्त की त्रिज्याएँ)
AB=AB (उभयनिष्ठ है)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से
\triangle ACB \cong \triangle ADB \\ \angle ACB=\angle ADB (CPCT से)
Example:2.एक वृत्त की 5cm और 11cm लम्बी दो जीवाएँ AB और CD समान्तर हैं और केन्द्र की विपरीत दिशा में स्थित हैं।यदि AB और CD के बीच दूरी 6cm हो तो वृत्त की त्रिज्या ज्ञात कीजिए।
Solution:ज्ञात है:O,वृत्त का केन्द्र और AB=5 सेमी तथा CD=11 सेमी है।
रचना (Construction): OL \perp AB तथा OM \perp CD खींचा।
चूँकि केन्द्र से जीवा पर लम्ब,जीवा को समद्विभाजित करता है।
इसलिए OL=2.5 सेमी और CM=5.5 सेमी
माना वृत्त की त्रिज्या r है।
\triangle ALO में
AO^2=OL^2+AL^2 \\ \Rightarrow r^2=x^2+(2.5)^2 \\ \Rightarrow r^2=x^2+6.25 \ldots(1) \\ \triangle CMO में
OC^2=LM^2+OM^2 \\ \Rightarrow r^2=(5.5)^2+(6-x)^2 \\ \Rightarrow r^2=30.25+36-12 x+x^2 \\ \Rightarrow r^2=66.25-12 x+x^2 \cdots(2)
(1) व (2) से:
x^2+6.25=66.25-12 x+x^2 \\ \Rightarrow 12 x=66.25-6.25 \\ \Rightarrow 12 x=60 \\ \Rightarrow x^2=\frac{60}{12} \\ \Rightarrow x=5
समीकरण (1) में रखने पर:
r^2=5^2+6-25 \\ =25+\frac{625}{100} \\=25+\frac{25}{4} \\ =\frac{100+25}{4} \\ =\frac{125}{4} \\ \Rightarrow r =\sqrt{\frac{125}{4}} \\ \Rightarrow r =\frac{5 \sqrt{5}}{2} \text { सेमी }
Example:3.किसी वृत्त की दो समान्तर जीवाओं की लम्बाईयाँ 6cm और 8cm हैं।यदि छोटी जीवा केन्द्र से 4 सेमी की दूरी पर हो तो दूसरी जीवा केन्द्र से कितनी दूर है?
Solution:ज्ञात है:एक वृत्त जिसका केन्द्र O है।जीवा AB=6 सेमी, जीवा CD=8 सेमी है।
रचना (Construction): OP \perp AB और OQ \perp CD खींचा।
AP=3 सेमी तथा OP=4 सेमी
माना OQ=x
माना त्रिज्या=r सेमी
\triangle AOP में
A O^2=O P^2+A P^2 \\ \Rightarrow r^2=4^2+3^2 \\ \Rightarrow r^2=16+9=25 \cdots(1) \\ \triangle OCQ में
OC^2=O Q^2+C Q^2 \\ \Rightarrow r^2=x^2+4^2 \\ \Rightarrow r^2=x^2+16 \\ x^2+16=25 \\ \Rightarrow x^2=25-16 \\ \Rightarrow x^2=9 \\ \Rightarrow x=\sqrt{9} \\ \Rightarrow x=3 सेमी
अतः केन्द्र से दूसरी जीवा की दूरी=3 सेमी
Example:4.मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर AD और CE काटती हैं।सिद्ध कीजिए कि \triangle ABC जीवाओं AC और DE द्वारा केन्द्र पर अन्तरित कोणों के अन्तर का आधा है।
Solution:दिया है (Given):कोण ABC का शीर्ष B एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD और CE काटती है।
सिद्ध करना है (To Prove): \angle ABC=\frac{1}{2}(\angle A O C-\angle D O E)
रचना (Construction):CD को मिलाया।
उपपत्ति (Proof): \triangle BCD में
\angle ADC=\angle DBC+\angle DCB \cdots(1)
[किसी त्रिभुज में बहिष्कोण अपने दोनों अन्तराभिमुख कोणों के योग के बराबर होता है]
\angle ADC=\frac{1}{2} \angle AOC \cdots(2)
[किसी चाप द्वारा केन्द्र पर अन्तरित कोण उसके वृत्त के शेष भाग के किसी बिन्दु पर अन्तरित कोण का दुगुना होता है।]
इसी प्रकार \angle DCB=\frac{1}{2} \angle DOE \cdots(3)
समीकरण (2) व (3) से समीकरण (1) में मान रखने पर:
\frac{1}{2} \angle A O C=\angle D B C+\frac{1}{2} \angle D O E \\ \Rightarrow \angle DBC=\frac{1}{2} \angle A O C-\frac{1}{2} \angle D O E \\ \Rightarrow \angle D B C=\frac{1}{2}(\angle AOC-\angle DOE)
Example:5.सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिन्दु से होकर जाता है।
Solution:दिया है (Given):ABCD एक समचतुर्भुज है।AC और BD इसके दो विकर्ण हैं।
सिद्ध करना है (To Prove):भुजा AB को व्यास मानकर खींचा गया समचतुर्भुज ABCD के विकर्णों के प्रतिच्छेद बिन्दु से होकर जाएगा।
उपपत्ति (Proof):समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।
\therefore \angle AEB=90^{\circ}
AB वृत्त का व्यास है अतः
\angle AEB=90^{\circ} (अर्धवृत्त का कोण)
(1) व (2) से:
AB को व्यास मानकर खींचा गया वृत्त E से होकर जाएगा।
Example:6.ABCD एक समान्तर चतुर्भुज है।A,B और C से जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है।सिद्ध कीजिए कि AE=AD
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है।A,B और C से जाने वाला वृत्त (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है।
सिद्ध करना है (To Prove):AE=AD
उपपत्ति (Proof):चक्रीय चतुर्भुज ABCE में
\angle AED+\angle ABC=180^{\circ} \cdots(1)
(चक्रीय चतुर्भुज के सम्मुख कोण सम्पूरक होते हैं)
\angle ABC=\angle ADC \cdots(2)
(समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं)
(1) व (2) से:
\angle AED+\angle ADC=180^{\circ} \cdots(3) \\ \angle ADC+\angle ADE=180^{\circ} \cdots(4) (रैखिक कोण युग्म अभिगृहीत से)
(3) व (4) से:
\angle A E D+\angle A D C=\angle A D C+\angle A D E \\ \Rightarrow \angle A E D=\angle A D E \\ \triangle A D E में
\angle A E D=\angle ADE (सिद्ध किया है)
\therefore AE=AD
(त्रिभुज के बराबर कोणों की अभिमुख भुजाएँ बराबर होती हैं)
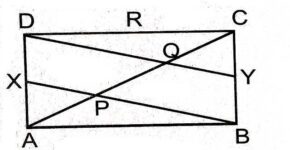
Example:7.AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं।सिद्ध कीजिए
(i)AC और BD व्यास हैं,
(ii)ABCD एक आयत है।
Solution:दिया है (Given):एक वृत्त की दो जीवाएँ AC और BD परस्पर O पर प्रतिच्छेद करती हैं।
सिद्ध करना है (To Prove):(i)AC और BD व्यास हैं,
(ii)ABCD एक आयत है।
रचना (Construction):AB,BC,CD और AD को मिलाया।
उपपत्ति (Proof):\triangle OAB और \triangle OCD में
OA=OC (दिया है)
\angle AOB=\angle COD
OB=OD (दिया है)
SAS सर्वांगसमता गुणधर्म से
\triangle OAB \cong \triangle OCD
AB=CD (CPCT से) ….(1)
इसी प्रकार \triangle AOD तथा \triangle BOC में
AD=BC …. (2)
(1) व (2) से:
AB+AD=BC+CD
\Rightarrow BAD=BCD
BD वृत्त को दो भागों में बाँटती है।
\Rightarrow BD व्यास है।
इसी प्रकार AC व्यास है।
(2)\triangle AOB \cong \triangle COD \\ \angle OAB अर्थात् \angle CAB=\angle OCD अर्थात् \angle ACD \\ \Rightarrow AB \parallel CD
पुन: \triangle AOD \cong \triangle BOC \\ \Rightarrow AD \| BC \\ \Rightarrow ABCD चक्रीय समान्तर चतुर्भुज है।
\angle DAB=\angle DCB \cdots \cdots(3) (समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं)
ABCD एक चक्रीय चतुर्भुज है।
\angle DAB+\angle DCB=180^{\circ} \cdots(4)
(3) व (4) से:
\angle DAB=\angle DCB=90^{\circ}
अतः ABCD एक आयत है।
Example:8.यदि त्रिभुज ABC के कोणों A,B और C के समद्विभाजक इसके परिवृत्त को क्रमशः D,E और F पर प्रतिच्छेद करते हैं।सिद्ध कीजिए कि त्रिभुज DEF के कोण 90^{\circ}-\frac{1}{2} A , 90^{\circ}-\frac{1}{2} B तथा 90^{\circ}-\frac{1}{2} C हैं।
Solution:दिया है (Given):एक जिसमें तथा के समद्विभाजक AD,BE और CD हैं।
सिद्ध करना है (To Prove): \angle D=90^{\circ}-\frac{1}{2} A \\ \angle E=90^{\circ}-\frac{1}{2} B \\ \angle F=90^{\circ}-\frac{1}{2} C
उपपत्ति (Proof):
\angle 1=\angle 2=\frac{1}{2} \angle A \\ \angle 3=\angle 4=\frac{1}{2} \angle B \\ \angle 5=\angle 6=\frac{1}{2} \angle C \\ \angle ADE=\angle 3(एक ही वृत्तखण्ड के कोण)………(1)
\angle A D F=\angle 6 (एक ही वृत्तखण्ड के कोण)…………..(2)
(1) व (2) को जोड़ने पर:
\angle A D E+\angle A D F=\angle 3+\angle 6 \\ \Rightarrow \angle D=\frac{1}{2} \angle B+\frac{1}{2} \angle C \\ \Rightarrow \angle D=\frac{1}{2}(\angle B+\angle C) \\ \Rightarrow \angle D=\frac{1}{2}\left(180^{\circ}-\angle A\right) ( \because \triangle A B C के तीनों कोणों का योग=180°)
\Rightarrow \angle D =90^{\circ}-\frac{1}{2} A
इसी प्रकार \angle E=90^{\circ}-\frac{1}{2} B \\ \angle F=90^{\circ}-\frac{1}{2} C
Example:9.दो सर्वांगसम वृत्त परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं।A से होकर कोई रेखाखण्ड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं।सिद्ध कीजिए कि BP=BQ है।
Solution:दिया है (Given):दो वृत्त जो कि सर्वांगसम है और A तथा B पर प्रतिच्छेद करते हैं।A से होकर एक रेखाखण्ड PAQ खींचा गया है जबकि P और Q वृत्त पर स्थित हैं।
सिद्ध करना है (To Prove):BP=BQ
रचना (Construction):A और B को मिलाया।
उपपत्ति (Proof):चूँकि दो वृत्त सर्वांगसम हैं।
AB इनकी उभयनिष्ठ जीवा है।अर्थात् AB की लम्बाई दोनों वृत्तों में बराबर है।
\therefore चाप ACB=चाप ADB
\Rightarrow \angle BPA=\angle BQA \\ \Rightarrow BP=BQ
Example:10.किसी त्रिभुज ABC में यदि का समद्विभाजक तथा BC का लम्ब समद्विभाजक प्रतिच्छेद करें,तो सिद्ध कीजिए कि वे \triangle ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
Solution:दिया है (Given):O केन्द्र वाले एक वृत्त के अन्दर \triangle ABC है।E वृत्त पर एक बिन्दु इस प्रकार है कि AE,\angle BAC का समद्विभाजक है तथा D,BC का मध्य-बिन्दु है।
सिद्ध करना है (To Prove):DE,BC का लम्ब समद्विभाजक है।
अर्थात् \angle BDE=\angle CDE=90^{\circ}
रचना (Construction):BE तथा EC को मिलाया।
उपपत्ति (Proof): \angle B A E=\angle C A E(दिया है)
चाप BE=चाप CE
\Rightarrow जीवा BE=जीवा CE …. (1)
\triangle BDE तथा \triangle CDE में
BE=CE [(1) से]
BD=CD (दिया है)
DE=DE (उभयनिष्ठ है)
SSS सर्वांगसमता गुणधर्म से
\triangle BDE \cong \triangle CDE \\ \Rightarrow \angle BDE=\angle CDE(CPCT से)
तथा \angle B D E+\angle C D E=180^{\circ} (रैखिक कोण युग्म)
\therefore \angle B D E=\angle CDE=90^{\circ}
अतः DE,BC का लम्ब समद्विभाजक है।
उपर्युक्त उदाहरणों के द्वारा एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Angle Subtended by Arc of Circle 9th),कक्षा 9 में एक वृत्त के चाप द्वारा अंतरित कोण (Angle Subtended by Arc of Circle in Class 9) को समझ सकते हैं।
3.एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 पर आधारित सवाल (Questions Based on Angle Subtended by Arc of Circle 9th):
(1.)एक वृत्त की त्रिज्या 5 सेमी है।इसकी दो जीवाएँ AB और AC इस प्रकार हैं कि AB=AC=6 सेमी।जीवा BC की लम्बाई ज्ञात कीजिए।
(2.)एक समद्विबाहु \triangle ABC में AB=AC और BC का मध्य-बिन्दु D है।सिद्ध कीजिए कि त्रिभुज की समान भुजाओं में किसी को भी व्यास मानकर वृत्त खींचने पर यह D से होकर जाएगा।
उपर्युक्त सवालों को हल करने पर एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Angle Subtended by Arc of Circle 9th),कक्षा 9 में एक वृत्त के चाप द्वारा अंतरित कोण (Angle Subtended by Arc of Circle in Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Angle Subtended by Arc of Circle
4.एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Frequently Asked Questions Related to Angle Subtended by Arc of Circle 9th),कक्षा 9 में एक वृत्त के चाप द्वारा अंतरित कोण (Angle Subtended by Arc of Circle in Class 9) से सम्बन्धित अक्सर पूछे जाने वाले
प्रश्न:1.अर्धवृत्त किसे कहते हैं? (What is a Semicircle?):
उत्तर:जब P और Q एक व्यास के सिरे हों तो दोनों चाप बराबर हों जाते हैं और प्रत्येक चाप को अर्धवृत्त (semicircle) कहते हैं।
प्रश्न:2.त्रिज्यखण्ड किसे कहते हैं? (What is a Sector?):
उत्तर:केन्द्र को एक चाप के सिरों से मिलाने वाली त्रिज्याओं एवं चाप के बीच के क्षेत्र को त्रिज्यखण्ड (sector) कहते हैं।
प्रश्न:3.वृत्त की मुख्य बातें लिखिए। (Write Down HIGHLIGHTS of Circle):
उत्तर:(1.)एक वृत्त किसी तल के उन सभी बिन्दुओं का समूह होता है,जो तल के स्थिर बिन्दु से समान दूरी पर हों।
(2.)एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र (या संगत केन्द्रों) पर बराबर कोण अन्तरित करती हैं।
(3.)यदि किसी वृत्त की (या सर्वांगसम वृत्तों की) दो जीवाएँ केन्द्र पर (या संगत केन्द्रों पर) बराबर कोण अन्तरित करें,तो जीवाएँ बराबर होती हैं।
(4.)किसी वृत्त के केन्द्र से किसी जीवा पर डाला गया लम्ब उसे समद्विभाजित करता है।
(5.)केन्द्र से होकर जाने वाली और किसी जीवा को समद्विभाजित करने वाली रेखा जीवा पर लम्ब होती है।
(6.)तीन असंरेखीय बिन्दुओं से जाने वाला एक और केवल एक वृत्त होता है।
(7.)एक वृत्त की (या सर्वांगसम वृत्तों की) बराबर जीवाएँ केन्द्र से (या संगत केन्द्रों से) समान दूरी पर होती हैं।
(8.)एक वृत्त के केन्द्र (या सर्वांगसम वृत्तों के केन्द्रों) से समान दूरी पर स्थित जीवाएँ बराबर होती हैं
(9.)यदि किसी वृत्त के दो चाप सर्वांगसम हों,तो उनकी संगत जीवाएँ बराबर होती हैं और विलोमत: यदि किसी वृत्त की दो जीवाएँ बराबर हों तो उनके संगत चाप (लघु,दीर्घ) सर्वांगसम होते हैं।
(10.)किसी वृत्त की सर्वांगसम चाप केन्द्र पर बराबर कोण अन्तरित करते हैं।
(11.)किसी चाप द्वारा केन्द्र पर अन्तरित कोण उसके द्वारा वृत्त के शेष भाग के किसी बिन्दु पर अन्तरित कोण का दुगुना होता है।
(12.)एक वृत्तखण्ड में बने कोण बराबर होते हैं।
(13.)अर्धवृत्त का कोण समकोण होता है।
(14.)यदि दो बिन्दुओं को मिलाने वाला रेखाखण्ड उसको अन्तर्विष्ट करने वाली रेखा के एक ही ओर स्थित दो अन्य बिन्दुओं पर समान कोण अन्तरित करे, तो चारों बिन्दु एक वृत्त पर स्थित होते हैं।
(15.)चक्रीय चतुर्भुज के सम्मुख कोणों के प्रत्येक युग्म का योग 180° होता है।
(16.)यदि किसी चतुर्भुज के सम्मुख कोणों के किसी एक युग्म का योग 180° हो,तो चतुर्भुज चक्रीय होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Angle Subtended by Arc of Circle 9th),कक्षा 9 में एक वृत्त के चाप द्वारा अंतरित कोण (Angle Subtended by Arc of Circle in Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Angle Subtended by Arc of Circle 9th
एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9
(Angle Subtended by Arc of Circle 9th)
Angle Subtended by Arc of Circle 9th
एक वृत्त के चाप द्वारा अंतरित कोण कक्षा 9 (Angle Subtended by Arc of Circle 9th) के इस
आर्टिकल में वृत्त,जीवा द्वारा एक बिन्दु पर अन्तरित कोण,तीन बिन्दुओं से जाने वाला वृत्त,समान
जीवाएँ और उनकी केन्द्र से दूरियाँ,एक चाप द्वारा अंतरित कोण तथा चक्रीय चतुर्भुज पर
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
