1.कोण एवं माप (Angle and Measurement):

Angle and Measurement

कोण एवं माप (Angle and Measurement):कोण (Angle):कोई किरण OA अपनी प्रारंभिक स्थिति OX से OA तक जाने में जितना घुमाव उत्पन्न करती है उसे कोण कहते हैं।इस प्रकार चित्र में XOA एक कोण है।कोण के लिए हम संकेत \angle  का प्रयोग करते हैं।साधारणतया कोणों के शीर्षों को अंग्रेजी वर्णमाला के बड़े अक्षरों यथा A,B,C,…. से तथा कोणों की माप को \alpha (अल्फा), \beta (बीटा), \gamma(गामा),\theta(थीटा), \phi(फाई), \psi (साई) आदि अक्षरों से व्यक्त किया जाता है।
धनात्मक तथा ऋणात्मक कोण:
यदि किरण OA अपनी प्रारंभिक स्थिति OX से प्रारंभ कर घड़ी की सुइयों के विपरीत दिशा में (वामावर्त) घूमती है तो इस प्रकार निर्मित कोण धनात्मक कोण है।चित्र में \angle XOA एक धनात्मक कोण है।

Angle and Measurement

यदि किरण OA अपनी प्रारंभिक स्थिति OX से घड़ी के सुइयों की दिशा में (दक्षिणावर्त) घूमती है तो इस प्रकार निर्मित कोण ऋणात्मक माना जाता है।अतः \angle XOA^{\prime} एक ऋणात्मक कोण है।
किसी भी परिमाण के कोण:
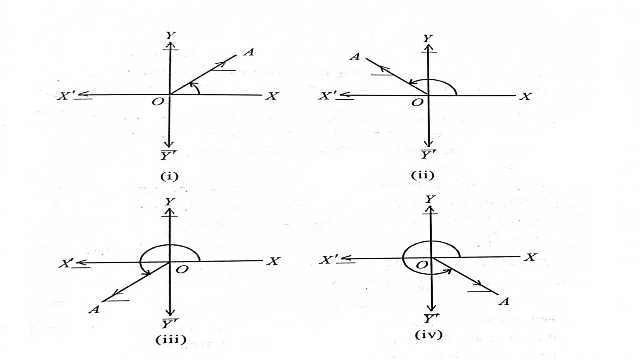
कोई परिक्रामी किरण OA अपनी प्रारंभिक स्थिति OX से प्रारंभ कर वामावर्त घूमकर प्रथम चतुर्थांश में जो कोण बनाती है वह 0° से 90° के मध्य होगा। उदाहरणार्थ:चित्र (i)में \angle XOA
(ii)कोई परिक्रामी किरण OA,अपनी प्रारंभिक स्थिति OX से प्रारंभ कर वामावर्त घूमकर द्वितीय चतुर्थांश में जो कोण बनाती है वह 90° से 180° के मध्य होगा।उदाहरणार्थ: चित्र (ii) में \angle XOA
(iii)कोई परिक्रामी किरण OA,अपनी प्रारंभिक स्थिति OX से प्रारंभ कर वामावर्त घूमकर तृतीय चतुर्थांश में जो कोण बनाती है वह 180° से 270° के मध्य होगा।उदाहरणार्थ: चित्र (iii) में \angle XOA
(iv)कोई परिक्रामी किरण OA,अपनी प्रारंभिक स्थिति OX से प्रारम्भ कर वामावर्त चतुर्थ चतुर्थांश में जो कोण बनाती है वह 270° से 360° के मध्य होगा।उदाहरणार्थ:चित्र (iv) में \angle XOA

Angle and Measurement

यदि किरण OA वामावर्त घूमकर एक पूरा चक्कर लगाकर अपनी प्रारंभिक स्थिति OX में आ जाती है तो वह 360° का कोण बनाती है और यदि दक्षिणावर्त घूमकर अपनी प्रारंभिक स्थिति में आ जाती है तो वह -360° का कोण बनाती है।
अब तक देखा कि कोण की अधिकतम माप 360° या 4 समकोण के बराबर हो सकती है किंतु कोण की माप 360° से अधिक हो सकती है।परिक्रामी किरण अपनी मूल स्थिति के परित: प्रत्येक पूर्ण चक्कर में 360° का कोण बनाती है।
यदि परिक्रामी किरण OA,अपनी प्रारंभिक स्थिति OX से प्रारंभ कर O के परित: पूरे दो चक्कर लगाती है तो वह 2 × 360°=720° का कोण बनाती है।यदि वह दो चक्कर लगाने के बाद पुनः OA की स्थिति में आ जाती है तो इस प्रकार निर्मित कोण=2 × 360°+\angle XOA  होता है।

Angle and Measurement

कोणों की माप (Measurement of Angles):
(i)षाष्टिक पद्धति (Sexagesimal System):इस पद्धति में हम कोण को अंश,मिनट तथा सेकंड में मापते हैं।इनके पारस्परिक संबंध निम्नलिखित हैं:
एक समकोण=नब्बे अंश=90°
एक अंश (1°)=साठ मिनट=60′
एक मिनट (1′)=60 सेकंड=60″
(ii)शतिक पद्धति (Centesimal System):इस पद्धति को फ्रांसीसी पद्धति भी कहते हैं।इस पद्धति को हम कोण को ग्रेड कला में मापते हैं तथा विकला में मापते हैं।इसके पारस्परिक संबंध निम्नलिखित हैं:
एक समकोण=100 ग्रेड= 100^{g}
एक ग्रेड ( 1^{g})=100 कला=100^{\prime}
एक कला (1′)=100 विकला=100^{\prime \prime}
(iii)वृत्तीय पद्धति (Circular System):इस पद्धति में कोण के माप की इकाई रेडियन (Radian) है।”किसी वृत्त के केंद्र पर उसकी त्रिज्या के बराबर लंबाई के चाप द्वारा अंतरित कोण एक रेडियन का होता है।”
माना किसी वृत्त की त्रिज्या r तथा केंद्र O है और वृत्त की परिधि पर कोई बिंदु A है।बिंदु A से एक चाप AB त्रिज्या r के बराबर लिया।इस प्रकार बना हुआ कोण एक रेडियन कहलाता है।प्रतीक द्वारा एक रेडियन 1^{c} द्वारा प्रदर्शित किया जाता है।अतः \angle AOB=1^{c}है।
माना वृत की परिधि पर कोई अन्य बिन्दु C है तो
\frac{ \angle AOC}{ \angle AOB}=\frac{\text{ चाप } AC}{\text{चाप } AB } \\ \Rightarrow \frac{ \angle AOC}{ \text{ चाप } AC}=\frac{\angle AOB}{\text{चाप } AB } \\ \angle AOC=\frac{\text{ चाप } AC }{\text{चाप } AB} \times \angle AOB \\=\frac{\text{ चाप } AC }{\text{चाप } AB} \times 1^{c} \\ \Rightarrow \angle AOC=\frac{\text{ चाप } AC }{\text{चाप } AB} \text{रेडियन} \cdots(1)
यदि \angle AOC=\theta^{c}(\theta रेडियन) तथा चाप AC=x हो तो समीकरण (1) से:
\theta^{c}=\frac{x}{r} \frac{\text{चाप}}{\text{त्रिज्या}} रेडियन
(पाई) का मान:किसी वृत्त की परिधि और उसके व्यास का अनुपात सदैव अचर होता है।इस अचर राशि को ग्रीक अक्षर (पाई) द्वारा व्यक्त किया जाता है जो अपरिमेय संख्या है।दशमलव के 8 स्थानों तक π का मान है 3.14159265 है, भिन्न रूप में इसका मान \frac{22}{7} लेते हैं।
रेडियन का मान:π=\frac{\text{वृत्त की परिधि}}{\text{वृत्त का व्यास}}
अतः यदि किसी वृत्त की त्रिज्या r हो तो उसका व्यास 2r तथा परिधि 2πr होती है।वृत्त के किसी चाप और उस चाप द्वारा केंद्र पर अंतरित कोण में एक निश्चित संबंध होता है:
\frac{ \angle AOB}{ 360^{\circ}}=\frac{\text{चाप } AB}{\text{वृत्त की परिधि}} \\ \frac{ \angle AOB}{ \text{चाप } AB}=\frac{360^{\circ} }{\text{वृत्त की परिधि}} \\  \frac{1^{c}}{r}=\frac{360^{\circ}}{2 \pi r} \\ \Rightarrow 1^{c}=\frac{180^{\circ}}{\pi} \cdots(1) \\ \Rightarrow 1^{c}=57^{\circ} 17^{\prime} 45^{\prime \prime} लगभग
(π का मान 3.1416 लेने पर)
इस प्रकार रेडियन का मान वृत्त की त्रिज्या पर निर्भर नहीं करता है।अर्थात् सभी वृत्तों के लिए एक रेडियन का मान अचर होता है।समीकरण (1) से: \pi^{c}=180^{\circ}
व्यवहार में चिन्ह c को छोड़ देते हैं और \pi^{c} के स्थान पर मात्र π का ही प्रयोग करते हैं।अर्थात्
180°=π

आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Remainder Theorem

2.कोण एवं माप के उदाहरण (Angle and Measurement Examples):

Example:1.5 सेमी त्रिज्या वाले वृत्त के केन्द्र पर 12 सेमी लम्बाई के चाप द्वारा कितने रेडियन का कोण बनेगा?
Solution:l=r \theta
l=12 सेमी,r=5 सेमी
\Rightarrow \theta=\frac{l}{r} \\ \Rightarrow \theta=\frac{12}{5} रेडियन
Example:2.किसी घड़ी के मिनट की सुई को \frac{3 \pi}{2} रेडियन कोण की रचना करने में कितना समय लगेगा?
Solution:\theta=\frac{3 \pi}{2}
4 समकोण=2π रेडियन
\because  घड़ी के मिनट की सुई को 2π रेडियन कोण की रचना करने में समय लगता है=1 घण्टा
\therefore घड़ी के मिनट की सुई को 1 रेडियन कोण की रचना करने में समय लगेगा=\frac{1}{2 \pi} घण्टा
\therefore   घड़ी के मिनट की सुई को रेडियन कोण की रचना करने में समय लगेगा=\frac{1}{2 \pi} \times \frac{3 \pi}{2} घण्टा

=\frac{3}{4} घण्टा= \frac{3}{4}\times 60 मिनट= 45 मिनट

Example:3.किसी घड़ी के मिनट की सुई को 120° के कोण की रचना करने में कितना समय लगेगा?
Solution: \because घड़ी की मिनट की सुई को 360° का कोण बनाने में समय लगता है=60 मिनट
\therefore घड़ी की मिनट की सुई को 1° का कोण बनाने में समय लगेगा=\frac{60}{360}
\therefore घड़ी की मिनट की सुई को 120° का कोण बनाने में समय लगेगा=\frac{60}{360} \times 120=20 मिनट
Example:4.किसी वृत्त में 10 सेमी लम्बाई का चाप केन्द्र पर 60° का कोण अन्तरित करता है तो वृत्त की त्रिज्या ज्ञात कीजिए।
Solution:\theta=60^{\circ},l=10.सेमी
\theta=60^{\circ} \times \frac{\pi}{ 180^{\circ} }=\frac{\pi}{3} रेडियन
\Rightarrow l=r \theta \\ \Rightarrow r=\frac{l}{\theta} =\frac{10}{\frac{\pi}{3}} \\ \Rightarrow r=\frac{30}{\pi} सेमी
Example:5 यदि ठीक दोपहर पश्चात् घड़ी के मिनट की सुई 30 समकोण परिक्रमण कर चुकी हो तो घड़ी में समय बताइए।
Solution:\because 4 समकोण की रचना करने में घड़ी के मिनट की सुई को समय लगता है=1 घण्टा
\therefore 1 समकोण की रचना करने में मिनट की सुई को समय लगेगा =\frac{1}{4} समकोण
\therefore 30 समकोण की रचना करने में मिनट की सुई को समय लगेगा=\frac{1}{4} समकोण ×30 समकोण =7 \frac{1}{2}घण्टा
अतः उस समय घड़ी में 7 बजकर 30 मिनट का समय होगा।
Example:6.किसी त्रिभुज के कोण 2:3:4 के अनुपात में हैं।तीनों कोणों को रेडियन में ज्ञात कीजिए।
Solution:त्रिभुज के कोणों का अनुपात=2:3:4
माना त्रिभुज के कोण=2x,3x,4x रेडियन है।

2x+3x+4x=\pi \\ \Rightarrow 9x=\pi \\ \Rightarrow x=\frac{\pi}{9}
अतः त्रिभुज के कोण

2x=2 \times \frac{\pi}{9}=\frac{2 \pi}{9} \\ 3x=3 \times \frac{\pi}{9}=\frac{3 \pi}{9} \\ 4x=4 \times \frac{\pi}{9}=\frac{4 \pi}{9}
अतः त्रिभुज के तीनों कोण हैं: \frac{2 \pi}{9},\frac{3 \pi}{9},\frac{4 \pi}{9}
Example:7.\frac{3 \pi}{5} रेडियन को षाष्टिक पद्धति में व्यक्त कीजिए।
Solution:1^{c}=\frac{180^{\circ}}{\pi} \\ \Rightarrow \frac{3 \pi}{5} \text{}=\frac{3 \pi}{5} \times \frac{180^{\circ}}{\pi} \\ =108^{\circ}
Example:8.निम्नलिखित कोणों को षाष्टिक पद्धति में व्यक्त कीजिए।

\text{(i)} \frac{\pi}{2} \text{(ii)} \frac{2 \pi}{5} \text{(iii)}\frac{5 \pi}{6} \text{(iv)}\frac{\pi}{15}
Solution: \text{(i)} \frac{\pi}{2} \times \frac{180^{\circ}}{\pi}=90^{\circ} \\ \text{(ii)} \frac{2 \pi}{5} \times \frac{180^{\circ}}{\pi}=72^{\circ} \\ \text{(iii)}\frac{5 \pi}{6} \times \frac{180^{\circ}}{\pi}=150^{\circ} \\ \text{(iv)}\frac{\pi}{15} \times \frac{180^{\circ}}{\pi}=12^{\circ}
Example:9.निम्नलिखित कोणों को रेडियन में परिवर्तित कीजिए।
(i)45° (ii)120° (iii)135° (iv)540°

Solution: \text{(i)} 45^{\circ} \times \frac{\pi}{180^{\circ}}=\frac{\pi}{4} \\ \text{(ii)} 120^{\circ} \times \frac{\pi}{180^{\circ}}=\frac{2 \pi}{3}\\ \text{(iii)}135^{\circ} \times \frac{\pi}{180^{\circ}}=\frac{3 \pi}{4} \\ \text{(iv)}540^{\circ} \times \frac{\pi}{180^{\circ}}=3\pi
उपर्युक्त उदाहरणों के द्वारा कोण एवं माप (Angle and Measurement) को समझ सकते हैं।

3.कोण एवं माप की समस्याएं (Angle and Measurement Examples):

(1.)\frac{\pi}{4} रेडियन को अंशों में परिवर्तित कीजिए।
(2.)किसी वृत्त के केंद्र पर \frac{\pi}{3} रेडियन का कोण अंतरित करने वाले चाप की लंबाई ज्ञात कीजिए।
(3.)किसी वृत्त की संपूर्ण परिधि द्वारा केंद्र पर अंतरित कोण ज्ञात कीजिए।
(4.)किसी घड़ी के मिनट की सुई को \frac{3 \pi}{2} रेडियन कोण की रचना करने में कितना समय लगेगा?
उत्तर (Answers):(1.)45° (2)\frac{\pi r}{3} (3)2 \pi^{c} (4.)45 मिनट
उपर्युक्त सवालों को हल करने पर कोण एवं माप (Angle and Measurement) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

4.मुख्य बिंदु (HIGHLIGHTS):

Angle and Measurement

(1.)परिक्रामी रेखा की वामावर्त दिशा में घूमने पर धनात्मक कोण और दक्षिणावर्त घूमने पर ऋणात्मक कोण बनता है।
(2.)कोणों को मापने की निम्नलिखित पद्धतियाँ हैं:
(i)षाष्टिक पद्धति (ii)शतिक पद्धति (iii)वृत्तीय पद्धति
(3.)षाष्टिक पद्धति में कोण को मापने की इकाई डिग्री है।
1समकोण=90°,1°=60′ (मिनट) तथा 1’=60″ (सैकण्ड)
(4.)किसी वृत्त के केंद्र पर बना वह कोण जो वृत्त की त्रिज्या के बराबर लंबाई के चाप द्वारा अंतरित होता है उसे एक रेडियन कहते हैं।वृत्तीय पद्धति में कोण को मापने की इकाई ‘रेडियन’ है।
(5.)वृत्त की संपूर्ण परिधि द्वारा उसके केंद्र पर अंतरित कोण 2π रेडियन होता है।
(6.)षाष्टिक व वृत्तीय पद्धति में संबंध D=\frac{180^{\circ}}{\pi}R होता हैं जहां D व R क्रमशः डिग्री व रेडियन में कोण हैं।

Also Read This Article:-Zeroes of polynomial

5.कोण एवं माप (Angle and Measurement) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:

 

कोण एवं माप (Angle and Measurement):कोण (Angle):कोई किरण OA अपनी प्रारंभिक स्थिति OX
से OA तक जाने में जितना घुमाव उत्पन्न करती है उसे कोण कहते हैं।इस प्रकार चित्र में XOA एक कोण है।