Area Between Two Curves Class 12
1.दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Area Between Two Curves Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves):
दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Area Between Two Curves Class 12) के इस आर्टिकल में दो वक्रों के मध्यवर्ती भाग को छायांकित करके वृहत् संख्या में पट्टियाँ काटकर क्षेत्रफल निश्चित समाकलन द्वारा ज्ञात करने पर आधारित सवालों को हल करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Area Under Simple Curves by Integral
2.दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 पर आधारित उदाहरण (Illustrations Based on Area Between Two Curves Class 12):
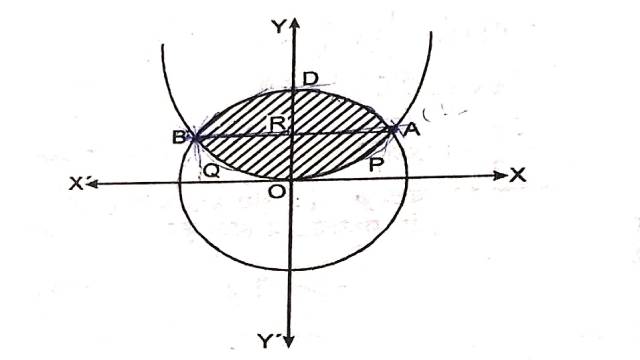
Illustration:1.परवलय x^2=4 y और 4 x^2+4 y^2=9 वृत्त के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:परवलय: x^2=4 y \cdots(1)
वृत्त: 4 x^2+4 y^2=9 \\ \Rightarrow x^2+y^2=\frac{9}{4} \cdots(2)
समीकरण (1) व (2) से:
4 y+y^2=\frac{9}{4} \\ \Rightarrow 16 y+4 y^2=9 \\ \Rightarrow 4 y^2+16 y-9=0 \\ \Rightarrow 4 y^2+18 y-2 y-9=0 \\ \Rightarrow 2 y(2 y+9)-1(2 y+9)=0 \\ \Rightarrow(2 y-1)(2 y+9)=0 \\ 2 y-1=0 \Rightarrow y=\frac{1}{2},2 y+9=0 \Rightarrow y=-\frac{9}{2} (असम्भव है)
y=\frac{1}{2} समीकरण (1) में रखने पर:
\Rightarrow x^2=4 \times \frac{1}{2} \Rightarrow x^2=2 \\ \Rightarrow x= \pm \sqrt{2}
अतः परवलय व वृत्त का प्रतिच्छेद बिन्दु A\left(-\sqrt{2}, \frac{1}{2}\right), B\left(\sqrt{2}, \frac{1}{2}\right) हैं।
अभीष्ट क्षेत्रफल=क्षेत्र OPADBQO का क्षेत्रफल
=2× क्षेत्र OPADRO का क्षेत्रफल
=2×[क्षेत्र OPARO का क्षेत्रफल+क्षेत्र ADRA का क्षेत्रफल]
=2 x \int_0^{\frac{1}{2}} x d y (परवलय से)+2 x \int_{\frac{1}{2}}^{\frac{3}{2}} x d y (वृत्त से)
=2 x \int_0^{\frac{1}{2}} \sqrt{4 y} d y+2 x \int_{\frac{1}{2}}^{\frac{3}{2}} \sqrt{\frac{9}{4}-y^2} d y \\ =2 \times 2\left[\frac{y^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^{\frac{1}{2}}+2 x\left[\frac{y \sqrt{\frac{9}{4}-y^2}}{2}+\frac{\frac{9}{2}}{2} \sin ^{-1}\left(\frac{y}{\frac{3}{2}}\right)\right]^{\frac{3}{2}} \\ =4 \times \frac{2}{3}\left[\left(\frac{1}{2}\right)^{\frac{3}{2}}-0\right]+\frac{9}{2} \sin ^{-1}\left(\frac{\frac{3}{2}}{\frac{3}{2}}\right)-\frac{1}{2} \sqrt{\frac{9}{4}-\frac{1}{4}} -\frac{9}{2} \sin ^{-1} \left(\frac{\frac{1}{2}}{\frac{3}{2}}\right) \\ =\frac{8}{3} \times \frac{1}{2 \sqrt{2}}+\frac{9}{2} \sin ^{-1}(1)-\frac{1}{2} \sqrt{2}-\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right) \\ =\frac{2 \sqrt{2}}{3}+\frac{9}{2} \times \frac{\pi}{2}-\frac{1}{\sqrt{2}}-\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right) \\ =\frac{4-3}{3 \sqrt{2}}+\frac{9}{2}\left(\frac{\pi}{2}-\sin ^{-1} \frac{1}{3}\right) \\ =\frac{1}{3 \sqrt{2}}+\frac{9}{2} \cos ^{-1} \frac{1}{3}\left[\because \sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}\right] \\ =\frac{\sqrt{2}}{6}+\frac{9}{2} \sin ^{-1}\left(\frac{2 \sqrt{2}}{3}\right) वर्ग इकाई
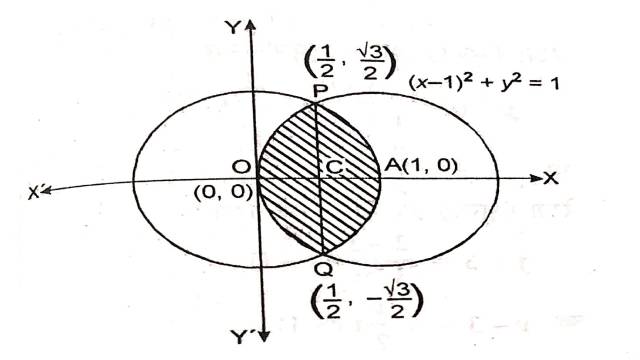
Illustration:2.वक्रों (x-1)^2+y^2=1 एवं x^2+y^2=1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:वृत्त (I): (x-1)^2+y^2=1 \\ \Rightarrow x^2-2 x+1+y^2=1 \\ \Rightarrow x^2-2 x+y^2=0 \cdots(1)
वृत्त (II): x^2+y^2=1 \cdots(2)
वृत्त (I) तथा (II) का प्रतिच्छेद बिन्दु समीकरण (1) व (2) से:
-2 x=-1 \Rightarrow x=\frac{1}{2}
समीकरण (2) में मान रखने पर:
\left(\frac{1}{2}\right)^2+y^2=1 \\ \Rightarrow y^2=1-\frac{1}{4} \Rightarrow y^2=\frac{3}{4} \\ \Rightarrow y= \pm \frac{\sqrt{3}}{2}
अतः दोनों वृत्तों का प्रतिच्छेद बिन्दु P\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right) , Q\left(\frac{1}{2}, -\frac{\sqrt{3}}{2}\right) हैं।दोनों वृत्तों के उभयनिष्ठ भाग को छायांकित करके दिखाया गया है जिसका समाकलन द्वारा क्षेत्रफल ज्ञात करना हैं।
अतः अभीष्ट क्षेत्रफल=क्षेत्र OQAPO का क्षेत्रफल
=2×क्षेत्र OAPO का क्षेत्रफल
=2 \int_0^{\frac{1}{2}} y d x (वृत्त (I) से)+ 2 \int_{\frac{1}{2}}^1 y dx (वृत्त (II) से)
=2 \int_0^{\frac{1}{2}} \sqrt{2 x-x^2} d x+2 \int_{\frac{1}{2}}^1 \sqrt{1-x^2} d x \\ =2 \int_0^{\frac{1}{2}} \sqrt{1-\left(x^2-2 x-1\right)} d x+2\left[\frac{x \sqrt{1-x^2}}{2}+\frac{1}{2} \sin^{-1} x\right]_{\frac{1}{2}}^1 \\ =2 \int_0^{\frac{1}{2}} \sqrt{1-(x-1)^2} d x+\sin ^{-1}(1)-\frac{1}{2} \sqrt{1-\frac{1}{4}} -\sin ^{-1}\left(\frac{1}{2}\right) \\ = 2\left[\frac{(x-1) \sqrt{2 x-x^2}}{2}+\frac{1}{2} \sin ^{-1}(x-1) \right]_0^{\frac{1}{2}}+\frac{\pi}{2}-\frac{1}{2} \cdot \frac{\sqrt{3}}{2}-\frac{\pi}{6} \\ = \left(\frac{1}{2}-1\right) \sqrt{2 \times \frac{1}{2}-\frac{1}{4}}+\sin ^{-1}\left(\frac{1}{2}-1\right)-\frac{1}{2} \sin ^{-1}(-1)+\frac{\pi}{2}-\frac{\pi}{6}-\frac{\sqrt{3}}{4} \\ =-\frac{1}{2} \cdot \frac{\sqrt{3}}{2}+\sin^{-1} \left(\frac{1}{2}\right)+\sin ^{-1}(1)+\frac{2 \pi}{6}-\frac{\sqrt{3}}{4} \\ =-\frac{\sqrt{3}}{2}-\sin ^{-1}\left(\frac{1}{2}\right)+\frac{\pi}{2}+\frac{\pi}{3} \\ =-\frac{\sqrt{3}}{2}-\frac{\pi}{6}+\frac{\pi}{2}+\frac{\pi}{3} \\ =-\frac{\sqrt{3}}{2}+\frac{(-\pi+3 \pi+2 \pi)}{6} \\ =\frac{4 \pi}{6}-\frac{\sqrt{3}}{2} \\ =\left(\frac{2\pi}{3}-\frac{\sqrt{3}}{2}\right) वर्ग इकाई
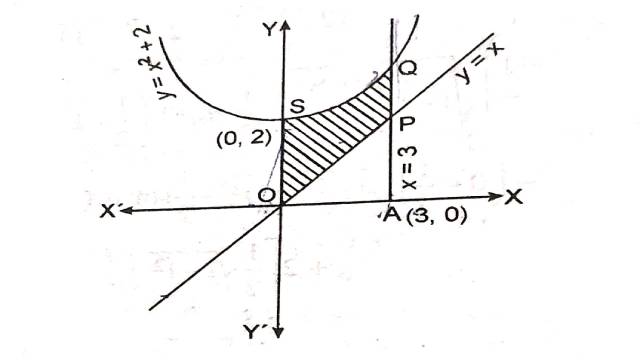
Illustration:3.वक्रों y=x^2+2, y=x,x=0 एवं x=3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
Solution:परवलय: x^2=y-2 \cdots(1)
y=x …. (2)
x=3 …..(3)
परवलय (1) व सरल रेखा (2) का प्रतिच्छेद बिन्दु
y^2=y-2 \Rightarrow y^2-y+2=0
स्पष्ट है कि सरल रेखा व परवलय आपस में प्रतिच्छेद नहीं करते हैं।
(2) व (3) का प्रतिच्छेद बिन्दु (3,3)
परवलय व रेखा x=3 का प्रतिच्छेद बिन्दु
(3)^2=y-2 \Rightarrow y=9+2=11
Q(3,11)
परवलय,सरल रेखा y=x तथा रेखा x=3 के बीच के क्षेत्र को छायांकित भाग द्वारा दर्शाया गया है।अतः
अभीष्ट क्षेत्रफल=क्षेत्र PQSOP का क्षेत्रफल
=क्षेत्र OAQSO का क्षेत्रफल-क्षेत्र OAP का क्षेत्रफल
=\int_0^3 y dx (परवलय से)-\int_0^3 y dx (सरल रेखा y=x से)
=\int_0^3\left(x^2+2\right) d x-\int_0^3 x d x \\ =\left[\frac{x^3}{3}+2 x\right]_0^3-\left[\frac{x^2}{2}\right]_0^3 \\ =\frac{27}{3}+2 \times 3-0-\frac{3^2}{2}-0 \\ =9+6-\frac{9}{2} \\ =\frac{18+12-9}{2} \\ =\frac{21}{2} वर्ग इकाई
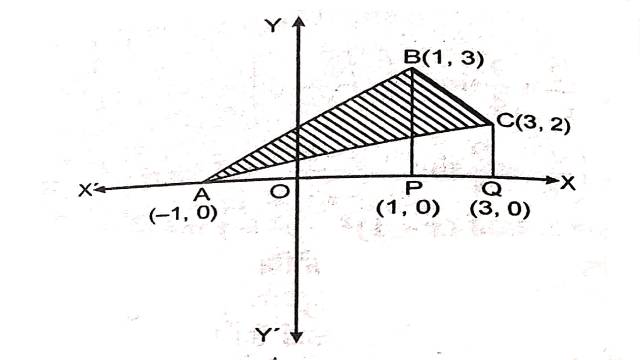
Illustration:4.समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-1,0),(1,3) एवं (3,2) हैं।
Solution:(-1,0),(1,3) से गुजरने वाली रेखा का समीकरण:
y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right) \\ \Rightarrow y-0=\frac{3-0}{1+1}(x+1) \\ \Rightarrow y=\frac{3}{2}(x+1) \cdots(1)
बिन्दु (1,3),(3,2) से गुजरने वाली रेखा का समीकरण:
y-3=\frac{2-3}{3-1}(x-1) \\ \Rightarrow y-3=-\frac{1}{2}(x-1) \\ \Rightarrow y=3 \frac{1}{2}(x-1) \\ =3-\frac{1}{2} x+\frac{1}{2} \\ \Rightarrow y=\frac{7}{2}-\frac{1}{2} x \cdots(2)
बिन्दु (-1,0),(3,2) से गुजरने वाली रेखा का समीकरण:
y-0=\frac{2-0}{3+1}(x+1) \\ \Rightarrow y =\frac{1}{2}(x+1) \cdots(3)
तीनों रेखाओं से घिरे हुए क्षेत्र अर्थात् त्रिभुज के क्षेत्र को छायांकित भाग द्वारा दर्शाया गया है जिसका समाकलन द्वारा क्षेत्रफल ज्ञात करना है।
अतः अभीष्ट क्षेत्रफल=\triangle ABC का क्षेत्रफल
=\triangle ABP का क्षेत्रफल+समलम्ब चतुर्भुज BPQC का क्षेत्रफल- \triangle AQC का क्षेत्रफल
=\int_{-1}^1 y d x (समीकरण (1) से)+\int_1^3 y dx (समीकरण (2) से)-\int_{-1}^{-1} y d x (समीकरण (3) से)
=\int_{-1}^1 \frac{3}{2}(x+1) d x+\int_1^3\left(\frac{1}{2}-\frac{1}{2} x\right) d x-\int_{-1}^3 \frac{1}{2}(x+1) d x \\ =\frac{3}{2}\left[\frac{x^2}{2}+x\right]_{-1}^1+\left[\frac{7}{2} x-\frac{1}{4} x^2\right]_1^3-\frac{1}{2}\left[\frac{x^2}{2}+x\right]_{-1}^3 \\ =\frac{3}{2}\left(\frac{1^2}{2}+1-\frac{(-1)^2}{2}+1\right) +\left[\frac{7}{2} \times 3-\frac{1}{4} \times 3^2-\frac{7}{2} \times 1+\frac{1}{4} \times 1^2\right]-\frac{1}{2}\left(\frac{3^2}{2}+3-\frac{(-1)^2}{2}+1\right) \\ =\frac{3}{2} \times \frac{3}{2}+\frac{3}{4}+\frac{21}{2}-\frac{9}{4}-\frac{7}{2}+\frac{1}{4}-\frac{1}{2}\left(\frac{17}{2}-\frac{1}{2}\right) \\ =\frac{9}{4}+\frac{3}{4}+\frac{21}{2}-\frac{9}{4}-\frac{7}{2}+\frac{1}{4}-\frac{4}{1} \\ =\frac{9+3+42-9-14+1-16}{4} \\ =\frac{16}{4} \\ =4 वर्ग इकाई
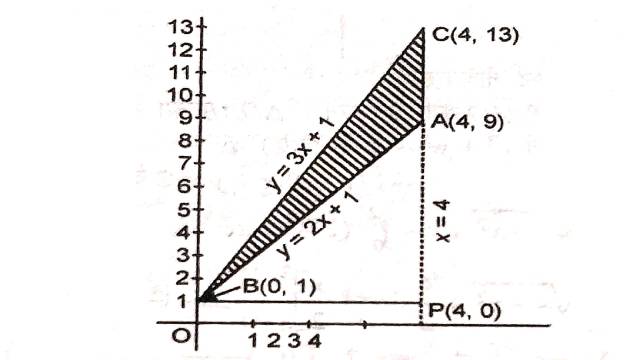
Illustration:5.समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के समीकरण y=2x+1,y=3x+1 एवं x=4 हैं।
Solution:y=2x+1 …. (1)
y=3x+1 ….. (2)
x=4 …… (3)
समीकरण (1) व (2) से:
3x+1=2x+1
x=0 तथा y=1
अतः B के निर्देशांक (0,1) हैं।
समीकरण (2) व (3) से:
y=3×4+1=13
बिन्दु C के निर्देशांक (4,13) हैं।
समीकरण (1) व (3) से:
y=2×4+1=9
बिन्दु A के निर्देशांक (4,9) हैं।
त्रिभुज ABC को छायांकित भाग द्वारा दर्शाया गया है जिसका समाकलन द्वारा क्षेत्रफल ज्ञात करना है।अतः
अभीष्ट क्षेत्रफल=समलम्ब चतुर्भुज BOPC का क्षेत्रफल-समलम्ब चतुर्भुज BOPA का क्षेत्रफल
=\int_0^4 y dx (समीकरण (2) से)-\int_0^4 y d x (समीकरण (1) से)
=\int_0^4(3 x+1) d x-\int_0^4(2 x+1) d x \\ =\left[\frac{3}{2} x^2+x\right]_0^4-\left[x^2+ x \right]_0^4 \\ =\frac{3}{2} \times 4^2+4-0-\left[4^2+4-0\right] \\ =3 \times 8+4-16-4 \\ =24-6 \\ =8 वर्ग इकाई
अतः \triangle ABC का क्षेत्रफल=8 वर्ग इकाई
प्रश्न 6 एवं 7 में सही उत्तर का चयन कीजिए:
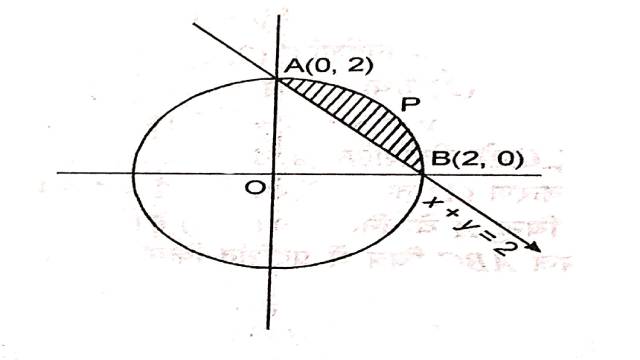
Illustration:6.वृत्त x^2+y^2=4 एवं रेखा x+y=2 से घिरे छोटे भाग का क्षेत्रफल है:
(A) 2(\pi-2) (B) \pi-2 (C) 2 \pi-1 (D) 2(\pi+2)
Solution:वृत्त: x^2+y^2=4 \cdots(1)
सरल रेखा: x+y=2 …. (2)
वृत्त तथा सरल रेखा का प्रतिच्छेद बिन्दु समीकरण (1) व (2) से:
(2-y)^2+y^2=4 \\ \Rightarrow 4-4 y+y^2+y^2=4 \\ \Rightarrow 2 y^2-4 y=0 \\ \Rightarrow y^2-2 y=0 \\ \Rightarrow y(y-2)=0 \Rightarrow y=0,2
जब y=0 तो (2) से x=2
जब y=2 तो (2) से x=0
अतः प्रतिच्छेद बिन्दु B(2,0),A(0,2)
वृत्त व सरल रेखा के उभयनिष्ठ भाग (छोटे भाग) को छायांकित भाग द्वारा दर्शाया गया है जिसका समाकलन द्वारा क्षेत्रफल ज्ञात करना है।अतः
अभीष्ट क्षेत्रफल=क्षेत्र OBPAO का क्षेत्रफल- \triangle OAB का क्षेत्रफल
=\int_0^2 y dx (वृत्त से)+ \int_0^2 y dx (सरल रेखा से)
=\int_0^2 \sqrt{4-x^2} d x -\int_0^2(2-x) d x \\ =\left[\frac{x \sqrt{4-x^2}}{2}+\frac{4}{2} \sin^{-1} \frac{x}{2}\right]_0^2-\left[2 x-\frac{x^2}{2}\right]_0^2 \\ =0+2 \sin ^{-1}\left(\frac{2}{2}\right)-0-\left(2 \times 2-\frac{2^2}{2}-0\right) \\ =2 \sin ^{-1}(1)-(4-2) \\ =2 \times \frac{\pi}{2}-2=\pi-2
अतः विकल्प (B) सही है।
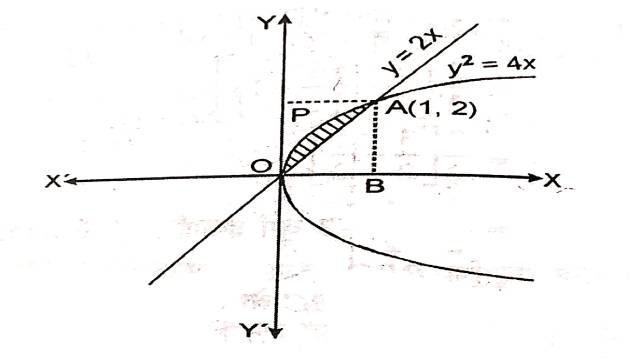
Illustration:7.वक्रों y^2=4 x एवं y=2x के मध्यवर्ती क्षेत्र का क्षेत्रफल है:
(A) \frac{2}{3} (B) \frac{1}{3} (c) \frac{1}{4} (D) \frac{3}{4}
Solution:परवलय: y^2=4 x \cdots(1)
सरल रेखा y=2x ….. (2)
परवलय व सरल रेखा का प्रतिच्छेद बिन्दु समीकरण (1) व (2) से:
(2 x)^2=4 x \\ \Rightarrow 4 x^2-4 x=0 \\ \Rightarrow 4 x(x-1)=0 \\ \Rightarrow x=0,1
जब x=0 तो (2) से y=0
जब x=1 तो (2) से y=2
अतः प्रतिच्छेद बिन्दु O(0,0),A(1,2) हैं।
सरल रेखा व परवलय के मध्यवर्ती भाग को छायांकित भाग द्वारा दर्शाया गया है जिसका क्षेत्रफल समाकलन द्वारा ज्ञात करना है।अतः
अभीष्ट क्षेत्रफल=क्षेत्र OPAO का क्षेत्रफल
=क्षेत्र OAPO का क्षेत्रफल- \triangle OAP का क्षेत्रफल
=\int_0^2 x dy (सरल रेखा से)- \int_0^2 x d y (परवलय से)
=\int_0^2 \frac{y}{2} d y-\int_0^2 \frac{y^2}{4} d y \\ =\frac{1}{4}\left[y^2\right]_0^2-\frac{1}{12} \left[y^3\right]_0^2 \\ =\frac{1}{4} \times 2^2-0-\left(\frac{1}{12} \times 2^3-0\right) \\ =1-\frac{2}{3} \\ =\frac{1}{3}
अतः विकल्प (B) सही है।
उपर्युक्त उदाहरणों के द्वारा दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Area Between Two Curves Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) को समझ सकते हैं।
3.दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 की समस्याएँ (Area Between Two Curves Class 12 Problems):
(1.)वक्र x^2+y^2=1 तथा x+y=1 से परिबद्ध प्रथम पाद में स्थित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
(2.)परवलय y=\frac{3 x^2}{4} और सरल रेखा 3x-2y+12=0 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
उत्तर (Answers):(1.) \frac{1}{4}(\pi-2) वर्ग इकाई (2.)27 वर्ग इकाई
उपर्युक्त सवालों को हल करने पर दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Area Between Two Curves Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) को ठीक से समझ सकते हैं।
Also Read This Article:- Definite Integral by Use of Properties
4.समाकलन गणित की ऐतिहासिक पृष्ठभूमि लिखिए। (Write the Historical Background of Integral Mathematics):
समाकलन गणित का प्रारंभ गणित के प्रारंभिक विकास काल से ही हुआ है।यह प्राचीन यूनानी गणितज्ञों द्वारा विकसित निःशेषता विधि पर आधारित है।इस विधि का प्रारंभ समतलीय आकृतियों के क्षेत्रफल और ठोस वस्तुओं के आयतन की गणना से हुआ।इस तरह से निःशेषता विधि,समाकलन विधि की प्रारंभिक स्थिति के रूप में समझी जा सकती है।निःशेषता विधि का सर्वोत्कृष्ट विकास प्रारंभिक काल में यूडोक्स (Eudoxus 440 ई.पू.) और आर्किमिडीज (Archimedes 300 ई. पू.) के कार्य से प्राप्त हुआ है।
कलन के सिद्धांत का क्रमबद्ध विकास ईसा के पश्चात् 17वीं शताब्दी में हुआ।सन् 1665 में न्यूटन ने कलन पर अपना कार्य प्रवाहन सिद्धांत (Theory of fluxion) के रूप में प्रारंभ किया।उन्होंने इस सिद्धांत का प्रयोग वक्र के किसी बिंदु पर स्पर्शी और वक्रता-त्रिज्या ज्ञात करने में किया।न्यूटन ने व्युत्क्रम फलन की धारणा से परिचय कराया और इसको प्रतिअवकलज (अनिश्चित समाकलन) या स्पर्शियों की व्युत्क्रम विधि (Inverse Method of tangents) का नामकरण किया।
1684-86, के बीच में लैवनिज़ (Leibnitz) ने एक प्रपत्र एकटा इरोडिटोरियम (Acta Eruditorum) में प्रकाशित किया और इसे कैलक्यूलस सम्मैटोरियस (calculous Summatorius) नाम दिया,क्योंकि यह अनंत छोटे क्षेत्रफलों के योगफल से संबंधित था,वहीं पर उन्होंने इसे योगफल के प्रतीक \int द्वारा व्यक्त किया।सन् 1696 ई. में उन्होंने जे. बरनौली (J. Bernoulli) के सुझाव को मानकर अपने प्रपत्र को कैलक्यूलस इंटेग्राली (Calculus Integrali) नाम में परिवर्तित कर दिया।यह न्यूटन द्वारा स्पर्शियों की व्युत्क्रम विधि के संगत था।
न्यूटन और लैवनिज़ दोनों ने पूर्णतः स्वतंत्र मार्ग अपनाया जो मूलतः भिन्न थे। तथापि उन दोनों के सिद्धांतों के संगत प्रतिफल तत्सम पाए गए।लैवनिज़ ने निश्चित समाकलन की धारणा का प्रयोग किया।
यह निश्चित है कि उन्होंने ही सर्वप्रथम प्रतिअवकलज और निश्चित समाकलन के बीच के संबंध को स्पष्टतया सराहा।
निष्कर्ष यह है कि समाकलन गणित के आधारभूत धारणाओं,सिद्धांतों तथा अवकलन गणित से इसके प्रारंभिक संबंधों का विकास पी.डी. फर्मा,न्यूटन और लैवनिज़ के कार्यों द्वारा 17वीं शताब्दी के अंत में हुआ।तथापि इसका औचित्य,सीमा की संकल्पना के आधार पर 19वीं शताब्दी के प्रारंभ में ए.एल. कोशी (A.L. Cauchy) के द्वारा किया गया।अंत में ली सोफी (Lie Sophie) का निम्नलिखित उद्धरण वर्णनीय है।”It may be said that the conceptions of differential quotient and integral which in their origin certainly go back to Archimedes were introduced in Science by the investigations of Kepler,Descartes,Cavalieri,Fermat and Wallis… The discovery that differentiation and integration are inverse operations belongs to Newton and Leibnitz”.
Also Read This Article:- Indefinite Integrals in Class 12th
5.दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Frequently Asked Questions Related to Area Between Two Curves Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.दो वक्रों का क्षेत्रफल कैसे ज्ञात करते हैं? (How to Find the Area Between Two Curves?):
उत्तर:लैबनिज की चेतना एवं अंतर्ज्ञान की सच्चाई के फलस्वरूप किसी क्षेत्र को प्रारम्भिक क्षेत्रफल की वृहत् संख्या में पट्टियाँ काटकर और इन प्रारम्भिक क्षेत्रफलों का योगफल ज्ञात कर,क्षेत्रफल के परिकलन की क्रिया समाकलन कहलाती है।कल्पना कीजिए,हमें दो वक्र y=f(x) और y=g(x) दिए हुए हैं जहाँ [a,b] में जैसा कि आकृति में दर्शाया गया है।दिए हुए वक्रों के समीकरण से y का उभयनिष्ठ मान लेते हुए इन दोनों वक्रों के प्रतिच्छेदक बिन्दु x=a तथा x=b द्वारा देय है।
समाकलन के सूत्र का स्थापन करने के लिए प्रारम्भिक क्षेत्रफल को उर्ध्वाधर पट्टियों के रूप में लेना सुविधाजनक है।जैसा कि आकृति में दर्शाया गया है।प्रारम्भिक पट्टी की ऊँचाई f(x)-g(x) एवं चौड़ाई dx है,इसलिए प्रारम्भिक क्षेत्रफल: dA=[f(x)-g(x)]
तथा कुल क्षेत्रफल A=\int_a^b[f(x)-g(x)] dx
प्रश्न:2.बिरखाॅफ के अनुसार गणित की परिभाषा लिखिए। (WRITE THE DEFINITION OF MATHEMATICS ACCORDING TO BIRKHOFF):
उत्तर:गणित का अध्ययन करना चाहिए क्योंकि गणित के माध्यम से ही प्रकृति की कल्पना की जा सकती है। -बिरखॉफ
(One should study Mathematics because it is only through Mathematics that nature can be conceived in hormonious form. -BIRKHOFF)
प्रश्न:3.दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात करने का वैकल्पिक तरीका लिखो। (Write the Alternative Method to Find the Area Between Two Curves):
उत्तर:A=[वक्र y=f(x),x-अक्ष तथा रेखाओं x=a,x=b से घिरे क्षेत्र का क्षेत्रफल]-[वक्र y=g(x),x-अक्ष एवं रेखाओं x=a,x=b से घिरे क्षेत्र का क्षेत्रफल]
=\int_a^a f(x)dx-\int_a^b g(x) dx \\ =\int_a^b[f(x)-g(x)] dx जहाँ [a,b] में f(x) \ge g(x)
उपर्युक्त प्रश्नों के उत्तर द्वारा दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Area Between Two Curves Class 12),दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल (Area Between Two Curves) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Area Between Two Curves Class 12
दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12
(Area Between Two Curves Class 12)
Area Between Two Curves Class 12
दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल कक्षा 12 (Area Between Two Curves Class 12) के
इस आर्टिकल में दो वक्रों के मध्यवर्ती भाग को छायांकित करके वृहत् संख्या में पट्टियाँ
काटकर क्षेत्रफल निश्चित समाकलन द्वारा ज्ञात करने पर आधारित सवालों को हल करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.