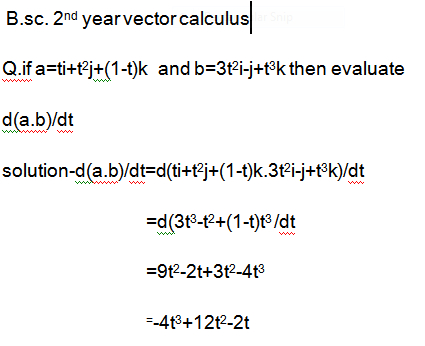Derivative of vectors
1.सदिशों का अवकलज (Derivative of vectors):
- सदिशों का अवकलज (Derivative of vectors) के इस आर्टिकल में दो सदिशों के अदिश गुणनफल को एक उदाहरण द्वारा समझाया गया है।
माना r=f(t), अदिश चर t का एकमानी एवं एकमानी फलन है।
माना t में लघुवृद्धि \delta{t} होने पर r में संगत वृद्धि \delta{r} होगी।
यदि \delta{t}\rightarrow{0} होने पर अनुपात \frac{\delta{r}}{\delta{t}} का सीमान्त मान अस्तित्वमय है तो \frac{dr}{dt} से प्रकट करते हैं और यह r का t के सापेक्ष अवकल गुणांक (differential coefficient) या अवकलज (derivative) कहलाता है।
अतः अब \frac{dr}{dt}=\lim_{\delta{t}\rightarrow{0}}\frac{\delta{r}}{\delta{t}}
\frac{dr}{dt}=\lim_{\delta{t}\rightarrow{0}}\frac{(r+\delta{r})-(r)}{\delta{t}}
\frac{dr}{dt}=\lim_{\delta{t}\rightarrow{0}}\frac{f(r+\delta{r})-f(r)}{\delta{t}}
अककल गुणांक को ज्ञात करने के प्रक्रम को अवकलज (differentiation) कहते हैं। - इस आर्टिकल में Derivative of vectors के बारे में उदाहरण के द्वारा समझाया गया है।इसका अर्थ है कि किसी सदिश का अवकलज ज्ञात करना। सामान्य अवकलज की तरह सदिश का अवकलज ज्ञात किया जाता है फर्क सिर्फ इतना है कि इसमें दिशा का ध्यान रखना होता है।जब किसी एक चर के सापेक्ष अवकलन ज्ञात करते हैं तो अन्य चरों को अचर मान लिया जाता है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Matrix Calculus
2.दो सदिशों के अदिश गुणनफल का अवकलज (Derivative of Scalar Product of Two Vectors):
- माना r=a.b
जहाँ a और b अदिश चर t के अवकलनीय फलन हैं।
अदिश चर t में लघुवृद्धि \delta{t} होने पर a और b में संगत वृद्धि \delta{a} और \delta{b} मानी जाएं तो
r+\delta{r}=(a+\delta{a}).(b+\delta{b})
\delta{r}=a.\delta{b}+\delta{a}.b+\delta{a}.\delta{b})
दोनों पक्षों में \delta{t} का भाग देने पर:
\frac{\delta{r}}{\delta{t}}=a.\frac{\delta{b}}{\delta{t}}+\frac{\delta{a}}{\delta{t}}.b+\frac{\delta{a}.\delta{b}}{\delta{t}}
जब \delta{t}\rightarrow{0} तब सीमा \delta{t}\rightarrow{0} लेने पर,
\frac{dr}{dt}=\lim_{{\delta{t}\rightarrow{0}}}\frac{\delta{r}}{\delta{t}}
\Rightarrow \frac{dr}{dt}=\underset{\delta \to 0}{Lt}[a.\frac{\delta{b}}{\delta{t}}+\frac{\delta{a}}{\delta{t}}.b+\frac{{\delta{a}}{\delta{b}}}{\delta{t}}]
=\underset{\delta \to 0}{Lt} a.\frac{\delta{b}}{\delta{t}}+\underset{\delta \to 0}{Lt}\frac{\delta{a}}{\delta{t}}.b+\underset{\delta \to 0}{Lt}\frac{\delta{a}}{\delta{b}}{\delta{t}}
=a.\frac{db}{dt}+\frac{da}{dt}.b+0 \left[\because {\delta{t}\rightarrow {0}}\Rightarrow \delta{b}\rightarrow{0}\right]
\therefore \frac{d}{dt}(a.b)=a.\frac{db}{dt}+\frac{da}{dt}.b
विशेष स्थिति:यदि a=b तब \frac{d}{dt}(a^{2})=2a.\frac{da}{dt}
Also Read This Article-Linear Differential Equations
- उपर्युक्त आर्टिकल में सदिशों का अवकलज (Derivative of vectors) के बारे में बताया गया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
No Responses