Period of Simple Harmonic Motion and amplitude
(1.)सरल आवर्त गति का आवर्तकाल और आयाम का परिचय (Introduction to Period of Simple Harmonic Motion and Amplitude):
- सरल आवर्त गति का आवर्तकाल और आयाम (Period of Simple Harmonic Motion and Amplitude):जब कोई कण एक सरल रेखा में एक ऐसे बल के अधीन गमन करे जो सरल रेखा पर स्थित किसी स्थिर बिन्दु से कण की दूरी के समानुपाती हो तथा जो सदैव उस बिन्दु की ओर दिष्ट हो तो कण की गति को सरल आवर्त गति कहते हैं।इसे संक्षेप में स.आ.ग. (S.H.M.) लिखते हैं।स्थिर बिन्दु गति केन्द्र कहलाता है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Simple harmonic motion
2.सरल आवर्त गति का आवर्तकाल और आयाम (Period of Simple Harmonic Motion and Amplitude):
- (1.)आयाम (Amplitude):चित्र में दूरी OA=OA’=a अर्थात् किसी भी विरामावस्था की बल केन्द्र से दूरी ‘d’ को आयाम (amplitude) कहते हैं।
- (2.)सरल आवर्त गति का आवर्तकाल (Period of S.H.M.):
नियत समय का अन्तराल जिसके पश्चात कण उसी स्थिति में आता है तथा उसी वेग से एक ही दिशा में गतिमान है आवर्त काल (period of motion) कहलाता है तथा गति को आवर्ती या नियतकालिक (Periodic) कहते हैं।
किसी समय t पर बल केन्द्र से कण की दूरी
x=a\sin{\sqrt{\mu}}t=a\sin(2n\pi+\sqrt{\mu}t)
=a\sin{\sqrt{\mu}}\left(\frac{2n\pi}{\sqrt{\mu}}+t\right)
पुनःv=\frac{dx}{dt}=a\sqrt{\mu}\cos{\sqrt{\mu}}t=a\sqrt{\mu}\cos(2n\pi+\sqrt{\mu}t)
=a\sqrt{\mu}\cos{\sqrt{\mu}}\left(\frac{2n\pi}{\sqrt{\mu}}+t\right)
इस प्रकार हम देखते हैं कि कण की स्थिति तथा वेग \frac{2\pi}{\sqrt{\mu}} समय के अन्तराल में समान रहती है अर्थात् \frac{2\pi}{\sqrt{\mu}} समयान्तराल से कण की गति दुहराई जाती है इसलिए इस अन्तराल को सरल आवर्त गति का आवर्तकाल कहते हैं।
अतः सरल आवर्त गति का आवर्तकाल (period of oscillation) होगा
T=\frac{2\pi}{\sqrt{\mu}}
जो कि आयाम पर निर्भर नहीं करता अर्थात् आवर्तकाल अचर है जबकि आयाम कुछ भी हो।
- उपर्युक्त आर्टिकल में सरल आवर्त गति का आवर्तकाल और आयाम (Period of Simple Harmonic Motion and Amplitude) के बारे में बताया गया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
One Response

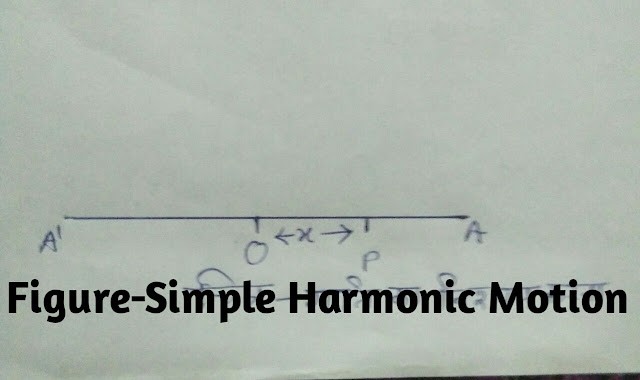






Bless you-ty-Is it ok to write more about this?