To Solve LPP by Simplex Method
1.रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method),सिम्पलेक्स विधि (Simplex Method):
रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method) इस आर्टिकल में सीखेंगे।इस पर आधारित सवालों के हल निम्नलिखित हैं:
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Improved Basic Feasible Solution
2.रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना के साधित उदाहरण (To Solve LPP by Simplex Method Solved Examples):
निम्न रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल कीजिए:
(Solve the following L.P.P. by simplex method):
Example :1.अधिकतम (max.) Z=3 x_1+2 x_2
प्रतिबन्ध (s.t.) x_1+x_2 \leq 4 \\ x_1-x_2 \leq 2
तथा (and) x_1, x_2 \geq 0
Solution:प्रतिबन्ध असमिकाओं में न्यूनतापरक x_3, x_4 चरों को सम्मिलित करने से समस्या का मानक रूप होगा:
अधिकतम Z=3 x_1+ 2 x_2+0 x_3+0 x_4
प्रतिबन्ध x_1+x_2+x_3+0 x_4=4 \\ x_1-x_2+0 x_3+x_4=2
तथा x_1, x_2, x_3, x_4 \geq 0
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
A=\left[\begin{array}{cccc} 1 & 1 & 1 & 0 \\ 1 & -1 & 0 & 1 \end{array}\right]=\left(\alpha_1 \quad \alpha_2 \quad \alpha_3 \quad \alpha_4\right) (मान लो)
\therefore \left(\alpha_3 \quad \alpha_4\right)=I_2, अतः प्रारम्भिक आधार B=\left( \alpha_3 \quad \alpha_4\right) एवं प्रारम्भिक सारणी निम्न होगी:
प्रथम सिम्पलेक्स सारणी

Z_{j}-C_{j} के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। Z_{1}-C_{1}=-3 निम्नतम है अतः नवीन आधारी हल हेतु \alpha_1 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i1}}, y_{i1}>0\right\}=\text{निम्नतम} \left(\frac{4}{1}, \frac{2}{1}\right) \\ =\frac{2}{1}=\frac{x_{B2}}{y_{21}} \\ \therefore y_{21}
अर्थात् 1 मुख्य अवयव (key element) तथा B_{2} अर्थात् \alpha_4 अपगामी सदिश होगा।अतः अन्य रूपान्तरणों द्वारा नवीन सारणी निम्न प्रकार होगी:
द्वितीय सिम्पलेक्स सारणी की पंक्तियों को तैयार करने की विधि (working rule):
मुख्य अवयव वाली पंक्ति:प्रथम सिम्पलेक्स सारणी की द्वितीय पंक्ति (मुख्य अवयव वाली पंक्ति) के प्रत्येक अवयव को मुख्य अवयव y_{21} से भाग देने पर मुख्य अवयव वाली पंक्ति तैयार हो जाएगी।
प्रथम पंक्ति:प्रथम सारणी की प्रथम पंक्ति के अवयवों में से मुख्य अवयव वाली नवीन पंक्ति को मुख्य अवयव के संगत प्रथम पंक्ति के अवयव से गुणा करके घटा देते हैं:
4-2×1=2
1-1×1=0
1-(-1)×1=2
1-0×1=1
0-1×1=-1
द्वितीय सिम्पलेक्स सारणी

Z_{j}-C_{j} के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। Z_{2}-C_{2}=-5 निम्नतम है अतः नवीन आधारी हल हेतु \alpha_2 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{\mathrm{Bi}}}{y_{i2}}, y_{i2}>0\right\}=\text{निम्नतम} \left(\frac{2}{1}\right) \\ =\frac{2}{1}=\frac{x_{B1}}{y_{12}} \\ \therefore y_{12}
अर्थात् 2 मुख्य अवयव (key element) तथा \alpha_3 अपगामी सदिश एवं 2 मुख्य अवयव होगा।
अब नवीन सारणी अर्थात् तृतीय सारणी निम्न प्रकार होगी:
तृतीय सारणी की पंक्तियों को तैयार करने की विधि (working rule):
मुख्य अवयव वाली पंक्ति:मुख्य अवयव वाली पंक्ति अर्थात् प्रथम पंक्ति को 2 से भाग देने पर मुख्य अवयव वाली पंक्ति तैयार हो जाएगी
\frac{2}{2}=1 \\ \frac{0}{2}=0 \\ \frac{2}{2}=1 \\ \frac{1}{2}=\frac{1}{2} \\ -\frac{1}{2}=-\frac{1}{2}
द्वितीय पंक्ति को तैयार करना:द्वितीय सारणी की द्वितीय पंक्ति के प्रत्येक अवयव में से तृतीय सारणी के मुख्य अवयवों अर्थात् उपर्युक्त अवयवों को मुख्य अवयव के संगत द्वितीय पंक्ति का अवयव अर्थात् (-1) से गुणा करके घटा देते हैं:
2-1 \times-1=3 \\ 1-0 \times-1=1 \\ -1-1 \times-1=0 \\ 0-\frac{1}{2} \times -1=\frac{1}{2} \\ 1-\left(\frac{-1}{2}\right) \times-1=\frac{1}{2}
तृतीय सिम्पलेक्स सारणी

सारणी में Z_{j}-C_{j} के सभी मान धनात्मक (\geq )हैं।अतः आधारी हल इष्टतम हल है जो निम्न प्रकार है:
x_1=3, x_2=1
तथा अधिकतम (max.) z=3 x_1+2 x_2 \\=3 \times 3+2 \times 1=11
Example:2.अधिकतम (max.) z=3 x_1+4 x_2+5 x_3
प्रतिबन्ध (s.t.) x_1+2 x_2+3 x_3 \leq 150 \\ x_1+2 x_2+x_3 \leq 120 \\ x_1+2 x_2 \leq 90
तथा (and) x_1, x_2, x_3 \geq 0
Solution:प्रतिबन्ध असमिकाओं में न्यूनतापरक चरों x_4, x_5 तथा x_6 को सम्मिलित करने से समस्या का मानक रूप होगा:
max(z)=3 x_1+4 x_2+5 x_3+0 x_4+0 x_5+0 x_6 \\ x_1+2 x_2+3 x_3+x_4+0 x_5+0 x_6=150 \\ x_1+2 x_2+x_3+0 x_4+x_5+0 x_6=120 \\ x_1+2 x_2+0 x_3+0 x_4+0 x_{5}+x_6=90
तथा x_1, x_2, x_3, x_4 ,x_5 ,x_6 \geq 0
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
A=\left[\begin{array}{llllll} 1 & 2 & 3 & 1 & 0 & 0 \\ 1 & 2 & 1 & 0 & 1 & 0 \\ 1 & 2 & 0 & 0 & 0 & 1\end{array}\right]=\left(\alpha_1 \quad \alpha_2 \quad \alpha_3 \quad \alpha_4 \quad \alpha_5 \quad \alpha_6\right) (मान लो)
\therefore \left(\alpha_4 \quad \alpha_5 \quad \alpha_6\right)=I_3, अतः प्रारम्भिक आधार B=\left( \alpha_4 \quad \alpha_5 \quad \alpha_6 \right) एवं प्रारम्भिक सारणी निम्न होगी:
प्रथम सिम्पलेक्स सारणी

z_j-c_j के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। z_3-c_3=-5 निम्नतम है अतः नवीन आधारी हल हेतु \alpha_3 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i3}}, y_{i3}>0\right\}=\text{निम्नतम} \left(\frac{150}{3}, \frac{120}{1}\right) \\ =\frac{150}{3}=\frac{x_{B1}}{y_{13}} \\ \therefore y_{13} अर्थात् 3 मुख्य अवयव (key element) तथा \alpha_4 अपगामी सदिश होगा।अतः अन्य रूपान्तरणों द्वारा नवीन सारणी निम्न प्रकार होगी:
द्वितीय सिम्पलेक्स सारणी की पंक्तियों को तैयार करने की विधि (working rule):
मुख्य अवयव वाली पंक्ति:मुख्य अवयव वाली पंक्ति प्रथम सारणी की पंक्ति है।प्रथम पंक्ति के सभी अवयवों को 3 (मुख्य अवयव) से भाग देने पर द्वितीय सारणी की प्रथम पंक्ति तैयार होगी।
\frac{150}{3}=50, \frac{1}{3}, \frac{2}{3}, 1, \frac{1}{3}, 0,0
अन्य पंक्तियां:द्वितीय पंक्ति:प्रथम सारणी की द्वितीय पंक्ति के अवयवों में से द्वितीय सारणी की प्रथम पंक्ति (मुख्य अवयव वाली पंक्ति) अर्थात् उपर्युक्त अवयवों को प्रथम सारणी में मुख्य अवयव के संगत अवयव अर्थात् 1 से गुणा करके घटा देंगे:
120-50 \times 1=70 \\ 1-\frac{1}{3} \times 1=\frac{2}{3} \\ 2-\frac{2}{3} \times 1=\frac{}{3} \\ 1-1 \times 1=0 \\ 0-\frac{1}{3} \times 1=-\frac{1}{3} \\ 1-0 \times 1=1 \\ 0-0 \times 1=0
तृतीय पंक्ति:प्रथम सारणी की तृतीय पंक्ति के अवयवों में से उपर्युक्त मुख्य अवयव वाली पंक्ति के अवयवों को मुख्य अवयव के संगत अवयव अर्थात् 0 से गुणा करके घटा देते हैं।
90-50 \times 0=90 \\1-\frac{1}{3} \times 0=1 \\2-\frac{2}{3} \times 0=2 \\0-1 \times 0=1 \\0-\frac{1}{3} \times 0=0 \\ 0-0 \times 0=0 \\1-0 \times 0=1
द्वितीय सिम्पलेक्स सारणी

z_j-c_j के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। z_1-c_1=-\frac{4}{3} निम्नतम है अतः नवीन आधारी हल हेतु \alpha_1 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i1}}, y_{i1}>0\right\}=\text{निम्नतम} \left(\frac{50}{\frac{1}{3}}, \frac{70}{\frac{2}{3}},\frac{90}{1}\right) \\ =\frac{90}{1}=\frac{x_{B3}}{y_{31}} \\ \therefore y_{31} अर्थात् 1 मुख्य अवयव (key element) तथा \alpha_6 अपगामी सदिश होगा।अब नवीन सारणी अर्थात् तृतीय सारणी निम्न प्रकार होगी:
तृतीय सारणी निम्न प्रकार होगी:
तृतीय सिम्पलेक्स सारणी को तैयार करने की विधि (working rule):
मुख्य अवयव वाली पंक्ति:मुख्य अवयव वाली पंक्ति द्वितीय सारणी की तृतीय पंक्ति है।अतः तृतीय पंक्ति को मुख्य अवयव 1 से भाग देने पर तृतीय सारणी की तृतीय पंक्ति तैयार होगी।
\frac{90}{1}=90, \frac{1}{1}=1, \frac{2}{1}=2, \frac{1}{1}=1, \frac{0}{1}=0,\frac{0}{1}=0, \frac{1}{1}=1
अन्य पंक्तियां:प्रथम पंक्ति:द्वितीय सारणी की प्रथम पंक्ति के अवयवों में से तृतीय सारणी के जो अवयव ऊपर तैयार किए हैं (मुख्य अवयव वाली पंक्ति के अवयव) उन्हें मुख्य अवयव के संगत अवयव अर्थात् से गुणा करके घटा देने पर प्रथम पंक्ति (तृतीय सारणी हेतु) तैयार होगी
50-90 \times \frac{1}{3}=20 \\ \frac{1}{3}-1 \times \frac{1}{3}=0 \\ \frac{2}{3}-2 \times \frac{1}{3}=0 \\ 1-1 \times \frac{1}{3}=\frac{2}{3} \\ \frac{1}{3}-0 \times \frac{1}{3}=\frac{1}{3} \\ 0-0 \times \frac{1}{3}=0 \\ 0-1 \times \frac{1}{3}=-\frac{1}{3}
द्वितीय पंक्ति:द्वितीय सारणी की द्वितीय पंक्ति के अवयवों में से तृतीय सारणी के लिए तैयार की गई पंक्ति (मुख्य अवयव वाली पंक्ति) के अवयवों से मुख्य अवयव के संगत अवयव से गुणा करके घटा देते हैं तो तृतीय सारणी के लिए द्वितीय पंक्ति तैयार होगी
70-90 \times \frac{2}{3}=10 \\ \frac{2}{3}-1 \times \frac{2}{3}=0 \\ \frac{4}{3}-2 \times \frac{2}{3}=0 \\ 0-1 \times \frac{1}{3}=-\frac{2}{3} \\ -\frac{1}{3}-0 \times \frac{2}{3}=-\frac{1}{3} \\ 1-0 \times \frac{2}{3}=1 \\ 0-1 \times \frac{2}{3}=-\frac{2}{3}
तृतीय सिम्पलेक्स सारणी

उपर्युक्त सारणी में z_j-c_j के सभी मान \geq है,अतः इसका आधारी हल इष्टतम हल होगा जो निम्न प्रकार है:
x_1=90, x_2=0, x_3=20
अतः दी गई रैखिक प्रोग्रामन समस्या का इष्टतम हल है:
x_1=90, x_2=0, x_3=20
तथा अधिकतम (Max.)z=3 x_1+4 x_2+5 x_3
=3×90+4×0+5×20
=120+100=220
Example:3.अधिकतम (max.) z=2 x_1+4 x_2
प्रतिबन्ध (s.t.) 2 x_1+3 x_2 \leq 48 \\ x_1+3 x_2 \leq 42 \\ x_1+x_2 \leq 21
तथा (and) x_1, x_2 \geq 0
Solution:प्रतिबन्ध असमिकाओं में न्यूनतापरक चरों x_3, x_4 एवं कृत्रिम चर x_5 सम्मिलित करने पर समस्या का मानक रूप निम्न प्रकार होगा:
अधिकतम z=2 x_1+4 x_2+0 x_3+ 0x_4-Mx_5
प्रतिबन्ध 2 x_1+3 x_2+x_3+0 x_4+0 x_5=48 \\ x_1+3 x_2+0 x_3+x_4+0 x_5=42 \\ x_1+x_2+0 x_3+0 x_4+x_5=21
तथा x_1, x_2,x_3, x_4, x_5 \geq 0
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
A=\left[\begin{array}{lllll} 2 & 3 & 1 & 0 & 0 \\ 1 & 3 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 1 \end{array}\right]=\left(\alpha_1 \quad \alpha_2 \quad \alpha_3 \quad \alpha_4 \quad \alpha_5\right)(मान लो)
\therefore\left(\alpha_3 \quad \alpha_4 \quad \alpha_5\right)=I_3 अतः प्रारम्भिक आधार B=\left(\alpha_3 \quad \alpha_4 \quad \alpha_5\right) एवं प्रारम्भिक सारणी निम्न होगी:
प्रथम सिम्पलेक्स सारणी

उपर्युक्त सारणी में z_j-c_j कुछ मान ऋणात्मक हैं अतः इसका आधारी हल इष्टतम हल नहीं है। z_2-c_2=-M-4 निम्नतम है अतः नवीन आधारी हल हेतु \alpha_2 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i2}}, y_{i2}>0\right\}=\text{निम्नतम} \left\{\frac{48}{3}, \frac{42}{3}, \frac{21}{1}\right\} \\ =\frac{42}{3}=\frac{x_{B2}}{y_{22}} \\ \therefore y_{22}
अर्थात् 3 मुख्य अवयव (key element) तथा \alpha_4 अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों द्वारा नवीन सारणी का निर्धारण निम्न प्रकार होगा:
द्वितीय सिम्पलैक्स सारणी

उपर्युक्त सारणी में z_j-c_j के कुछ मान ऋणात्मक हैं अतः इसका आधारी हल इष्टतम हल नहीं है। z_{1}-c_1=-\frac{2 M}{3}-\frac{2}{3} निम्नतम है अतः नवीन आधारी हल हेतु \alpha_1 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i1}}, y_{i1}>0\right\}=\text{निम्नतम} \left\{\frac{6}{1}, \frac{14}{\frac{1}{3}}, \frac{7}{\frac{2}{3}}\right\} \\ =\frac{6}{1}=\frac{x_{B1}}{y_{11}} \\ \therefore y_{11} अर्थात् 1 मुख्य अवयव (key element) तथा \alpha_3 अपगामी सदिश होगा।सामान्य रूपान्तरणों द्वारा नवीन सारणी निम्न प्रकार होगी:
तृतीय सिम्पलेक्स सारणी

उपर्युक्त सारणी में z_j-c_j के कुछ मान ऋणात्मक हैं।अतः इसका आधारी हल इष्टतम हल नहीं है। z_4-c_4=-M-\frac{2}{3} निम्नतम है अतः नवीन आधारी हल हेतु \alpha_4 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i4}}, y_{i4}>0\right\}=\text{निम्नतम} \left\{\frac{12}{\frac{2}{3}}, \frac{3}{1}\right\}\\ =\frac{3}{1}=\frac{x_{B3}}{y_{34}} \\ \therefore y_{34} अर्थात् 1 मुख्य अवयव (key element) तथा \alpha_5 अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों द्वारा नवीन सारणी का निर्धारण निम्न प्रकार होगा:
चतुर्थ सिम्पलेक्स सारणी

सारणी में z_j-c_j के सभी मान धनात्मक है,अतः इसका हल इष्टतम हल है।अतः इस सारणी में जो हल प्राप्त होता है, वह इष्टतम हल है अर्थात् x_1=9, x_2=10
अधिकतम (Z)=2 x_1+4 x_2=2 \times 9+4 \times 10 =58
Example:4.अधिकतम (Max.) Z=2 x_1+3 x_2
प्रतिबन्ध (s.t.) -x_1+2 x_2 \leq 4 \\ x_1+x_2 \leq 6 \\ x_{1}+3 x_2+x_5 \leq 9
तथा(and) x_1, x_2 \geq 0
Solution:प्रतिबन्ध असमिकाओं में न्यूनतापरक चरों x_3, x_4 एवं कृत्रिम चर x_5 सम्मिलित करने पर समस्या का मानक रूप निम्न प्रकार होगा:
अधिकतम (Z)=2 x_1+3 x_2+0 x_3+2 x_4 -M x_5
प्रतिबन्ध -x_1+2 x_2+x_3+0 x_4+0 x_5=4 \\ x_1+x_2+0 x_3+x_4+0 x_5=6 \\ x_{1}+3 x_2+0 x_3+0 x_4+x_5=9
तथा x_1, x_2, x_3, x_4 \geq 0
प्रतिबन्ध निकाय का गुणांक मैट्रिक्स
A=\left[\begin{array}{ccccc}-1 & 2 & 1 & 0 & 0\\1 & 1 & 0 & 1 & 0 \\1 & 3 & 0 & 0 & 1\end{array}\right]=\left(\alpha_1 \quad \alpha_2 \quad \alpha_3 \quad \alpha_4 \quad \alpha_5 \right) (मानलो)
\therefore \left(\alpha_3 \quad \alpha_4 \quad \alpha_5\right)=I_3 , अतः प्रारम्भिक आधार B=\left(\alpha_3 \quad \alpha_4\right) एवं प्रारम्भिक सारणी निम्न होगी:
प्रथम सिम्पलेक्स सारणी

z_j-c_j के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। z_2-c_2=-3-3M निम्नतम है अतः नवीन आधारी हल हेतु \alpha_2 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i2}}, y_{i2}>0\right\}=\text{निम्नतम} \left\{\frac{4}{2}, \frac{6}{1}, \frac{9}{3}\right\} \\ =\frac{4}{2}=\frac{x_{B1}}{y_{12}} \\ \therefore y_{12} अर्थात् 2 मुख्य अवयव (key element) तथा \alpha_3 अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों द्वारा नवीन सारणी का निर्धारण निम्न प्रकार होगा:
द्वितीय सिम्पलेक्स सारणी

z_j-c_j के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। z_1-c_{1}=-\frac{5}{2}-\frac{7}{2} निम्नतम है अतः नवीन आधारी हल हेतु \alpha_1 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i1}}, y_{i1}>0\right\}=\text{निम्नतम} \left\{\frac{4}{\frac{3}{2}}, \frac{3}{\frac{5}{2}}\right\} \\ =\frac{3}{\frac{5}{2}}=\frac{x_{B3}}{y_{31}} \\ \therefore y_{31} अर्थात् मुख्य अवयव (key element) तथा \alpha_5 अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों द्वारा नवीन सारणी का निर्धारण निम्न प्रकार होगाः
तृतीय सिम्पलेक्स सारणी

z_j-c_j के कुछ मान ऋणात्मक होने के कारण आधारी हल इष्टतम हल नहीं है। z_3-c_3=-\frac{3}{5} निम्नतम है अतः नवीन आधारी हल हेतु \alpha_3 प्रवेशी सदिश होगा एवं
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{i3}}, y_{i3}>0\right\}=\text{निम्नतम} \left\{\frac{\frac{13}{5}}{\frac{1}{5}}, \frac{\frac{11}{5}}{\frac{2}{5}}\right\} \\ =\frac{\frac{11}{5}}{\frac{2}{5}} =\frac{x_{B2}}{y_{23}} \\ \therefore y_{23} अर्थात् \frac{2}{5} मुख्य अवयव (key element) तथा \alpha_4 अपगामी सदिश होगा।पुनः सामान्य रूपान्तरणों द्वारा नवीन सारणी का निर्धारण निम्न प्रकार होगा:
चतुर्थ सिम्पलेक्स सारणी
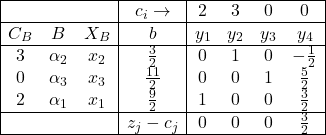
सारणी में z_j-c_j के सभी मान धनात्मक हैं अतः इसका हल इष्टतम हल है जो निम्न प्रकार है:
x_1=\frac{9}{2}, x_2=\frac{3}{2}
तथा अधिकतम Z=2 x_1+3 x_2 \\ =2 \times \frac{9}{2}+3 \times \frac{3}{2}=\frac{27}{2}
उपर्युक्त उदाहरणों के द्वारा रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method),सिम्पलेक्स विधि (Simplex Method) को समझ सकते हैं।
3.रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना के सवाल (To Solve LPP by Simplex Method Questions):
निम्न रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल कीजिए:
(Solve the following L.P.P. by simplex method):
(1) max. Z=x_1+x_2+3 x_2
s.t. 3 x_1+2 x_2+x_3 \leq 3 \\ 2 x_1+x_2+2 x_3 \leq 2
and x_1, x_2, x_3 \geq 0
(2.) max Z=3 x_1+5 x_2+4 x_{3}
s.t. 2 x_1+3 x_2 \leq 8 \\ 2 x_2+5 x_3 \leq 10
and x_1, x_2, x_3 \geq 0
उत्तर (Answers): (1.) x_1=0, x_2=0, x_3=1 \\ max. Z=3
(2.) x_1=\frac{89}{41}, x_2=\frac{50}{41} , x_{3}=\frac{62}{41} \\ \max. Z=\frac{765}{41}
उपर्युक्त सवालों को हल करने पर रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method),सिम्पलेक्स विधि (Simplex Method) को ठीक से समझ सकते हैं।
Also Read This Article:-Assignment Problems
4.रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (Frequently Asked Questions Related to To Solve LPP by Simplex Method),सिम्पलेक्स विधि (Simplex Method) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रवेशी सदिश से क्या तात्पर्य है? (What Do You Mean by Entering Vector?):
उत्तर:यदि सारणी का आधारी हल इष्टतम न हो तो नवीन उन्नत आधारी हल हेतु नये आधार के लिए प्रवेशी सदिश का चयन करते हैं?यदि सारणी की अन्तिम पंक्ति में z_j-c_j का निम्नतम मान (जो ऋणात्मक होता है) j=k के लिए प्राप्त हो तो \alpha_{k} प्रवेशी सदिश होता है,तब y_{k} के स्तम्भ के नीचे \uparrow चिन्ह को अंकित कीजिए।
प्रश्न:2.अपगामी सदिश से क्या तात्पर्य है? (What Do You Mean by Departing Vector?):
उत्तर:यदि प्रवेशी सदिश हो तो निम्न सूत्र द्वारा अपगामी सदिश का निर्धारण कीजिए
\underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{ij}}, y_{ik}>0\right\}
यह निम्नतम मान i=r के लिए प्राप्त हो तो y_{rk} मुख्य अवयव होगा तथा आधार की rवीं पंक्ति में स्थित सदिश अपगामी सदिश होगा।मुख्य अवयव पर * का चिन्ह या अवयव को \fbox{} में बन्द करते हैं तथा अपगामी सदिश के नीचे \downarrow चिन्ह अंकित करिए।
प्रश्न:3.सिम्पलेक्स सारणी का नवीन सारणी में रूपान्तरण कैसे करते हैं? (How to Transform of a Simplex Table to New Table?):
उत्तर:जब प्रथम सिम्पलेक्स सारणी से प्राप्त प्रारम्भिक आधारी हल इष्टतम नहीं होता है तो नवीन उन्नत सारणी का निर्धारण किया जाता है,जिसके लिए सर्वप्रथम z_j-c_j के मानों से प्रवेशी सदिश (entering vector) का चयन करते हैं।माना प्रवेशी सदिश हो तो प्रारम्भिक सारणी में y_{k} स्तम्भ के नीचे चिन्ह लगा देते हैं।तत्पश्चात अपगामी सदिश के निर्णय हेतु
सूत्र \underset{i}{\text{निम्नतम}} \left\{\frac{x_{Bi}}{y_{ij}}, y_{ik}>0\right\}
द्वारा मान ज्ञात किया जाता है,जो सदिश b तथा y_{k}(प्रवेशी सदिश) सदिश के संगत धनात्मक घटकों का निम्नतम अनुपात है।यदि यह अनुपात i=r के लिए निम्नतम हो तो rवीं पंक्ति में स्थित B का सदिश अपगामी सदिश होगा।सारणी में y_{r} के नीचे को \downarrow द्वारा चिन्हित कर देते हैं तथा \fbox{} मे बंद कर देते हैं ,क्योंकि यह अगले आधारी हल के निर्धारण हेतु मुख्य अवयव (key element) होता है।
प्रवेशी सदिश,अपगामी सदिश एवं मुख्य अवयव के निर्धारण के पश्चात नवीन आधारी हल अगली सारणी में सर्वप्रथम B स्तम्भ के अवयवों की पूर्ति करते हैं,जिसमें की जगह \alpha_k लिखा जाता है तथा अन्य घटक अपरिवर्तित रहते हैं। C_{B} तथा X_{B} सदिशों में भी B_r की पंक्ति के घटकों के संगत परिवर्तन (corresponding change) करके नई सारणी में यथास्थान लिख देते हैं।सारणी में शेष स्तम्भों की पूर्ति प्रकार करते हैं:
(1.)मुख्य अवयव वाली पंक्ति:नवीन सारणी के लिए मुख्य पंक्ति अर्थात् rवीं पंक्ति का मान पूर्व सारणी की r वीं पंक्ति के प्रत्येक अवयव को मुख्य अवयव y_{rk} का भाग देकर प्राप्त किया जाता है।[इस पंक्ति में C_{B},B तथा X_{B} स्तम्भों को सम्मिलित नहीं करते,क्योंकि उनका निर्धारण पहले कर लिया गया है]
(2.)अन्य पंक्तियां:नवीन सारणी की मुख्य अवयव वाली पंक्ति के अतिरिक्त अन्य किसी भी पंक्ति,माना कि i वीं पंक्ति का निर्धारण नई सारणी में मुख्य अवयव वाली पंक्ति (rवीं) के प्रत्येक अवयव को y_{ik} से गुणा कर पूर्व सारणी की संगत पंक्ति अर्थात् i वीं पंक्ति से घटा देते हैं।[इस पंक्ति में भी c_{B},B तथा X_{B} सम्मिलित नहीं करते]
(3.)अन्तिम पंक्ति:अन्तिम पंक्ति के अवयवों की गणना या तो z_{j}-c_{j}=c_{B}=y_{j}-c_{j} द्वारा करनी चाहिए या पूर्व में बताई गई विधि से करनी चाहिए।
इस प्रकार नवीन आधारी हल हेतु नई सिम्पलेक्स सारणी का निर्धारण करते हैं।यदि यह हल इष्टतम हो तो प्रक्रिया यहीं समाप्त हो जाती है,अन्यथा पुनः नवीन सारणी का निर्धारण करते हैं।इस प्रक्रिया की तब तक पुनरावृत्ति करते हैं जब तक कि इष्टतम हल प्राप्त न हो जाए।
उपर्युक्त प्रश्नों के उत्तर द्वारा रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex Method),सिम्पलेक्स विधि (Simplex Method) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
To Solve LPP by Simplex Method
रैखिक प्रोग्रामन समस्याओं को
सिम्पलेक्स विधि द्वारा हल करना
(To Solve LPP by Simplex Method)
To Solve LPP by Simplex Method
रैखिक प्रोग्रामन समस्याओं को सिम्पलेक्स विधि द्वारा हल करना (To Solve LPP by Simplex
Method) इस आर्टिकल में सीखेंगे।इस पर आधारित सवालों के हल निम्नलिखित हैं
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








