Arithmetic Mean and Mode in Statistics
1.सांख्यिकी में समान्तर माध्य और बहुलक (Arithmetic Mean and Mode in Statistics),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics):
सांख्यिकी में समान्तर माध्य और बहुलक (Arithmetic Mean and Mode in Statistics) के इस आर्टिकल में बहुलक,मध्यका और समान्तर माध्य से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Mode and Arithmetic Mean in Statistics
2.सांख्यिकी में समान्तर माध्य और बहुलक पर आधारित उदाहरण (Examples Based on Arithmetic Mean and Mode in Statistics):
Example:55.निम्नलिखित समंकों से समान्तर माध्य,मध्यका तथा बहुलक की गणना कीजिए:
(Calculate Mean,Median and Mode from the following figures):
![]()
Solution:Calculation of Mean,Median and Mode

समान्तर माध्य (\overline{X})=A+\frac{\sum f d x^{\prime}}{N} \times \\ =20+\frac{107}{140} \times 2 \\ =20+0.7642 \times 2 \\ =20+1.5284 \\ =21.5284 \\ \overline{X} \approx 21.53
मध्यका m=\frac{N}{2}=\frac{140}{2} \\ m=70
It lies in Median group 21-23
l_1=21, f=37, c=62, i=23-21=2
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =21+\frac{2}{37}(70-62) \\ =21+\frac{2}{37} \times 8 \\ =21+0.4324 \\ M \approx 21.43
निरीक्षण के द्वारा बहुलक वर्ग 19-21
l_1=19, i =21-19=2, f_1=44, f_0=10, f_2=37 \\ \Delta_1=f_1-f_0 =4 c_1-10=34 \\ \Delta_2=f_1-f_2 =44-37=7
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =19+\frac{34}{34+7} \times 2 \\ =19+\frac{68}{41} \\ =19+1.6585 \\ =20.6585 \\ Z \approx 20.66
समूहीकरण द्वारा

21-33 वर्ग पाँच बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।सूत्र द्वारा:
f_1=37_1 f_0=44, f_2=29 \\ \Delta_1=f_1-f_0=37-44=7 \\ \Delta_2=f_1-f_2=37-29=8
बहुलक (Z)=\ell_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =21+\frac{7}{7+8} \times 2 \\ =21+\frac{14}{15} \\ =21+0.933 \\ Z \approx 21.93
Example:56.निम्नलिखित से समान्तर माध्य,मध्यका तथा बहुलक ज्ञात कीजिए:
(Find Mean,Median and Mode from the following):

Solution:Calculation of Mean,Median and Mode

समान्तर माध्य (\overline{X})=A+\frac{\sum f d x^{\prime}}{N} \times i \\ =45+\frac{20}{150} \times 10 \\ =45+\frac{4}{3} \\ =45+1.333 \\ \overline{X} \approx 46.33
मध्यका m=\frac{N}{2}=\frac{150}{2} =75
It lies in Median group 40-50
l_1=40, f=41, c=56, i=50-40=10
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =40+\frac{10}{41}(75-56) \\ =40+\frac{10}{41} \times 19 \\ =40+\frac{190}{41} \\ =40+4.634 \\ \Rightarrow M \approx 44.63
बहुलक:निरीक्षण द्वारा बहुलक वर्ग 40-50
l_1=40, f_1=41, f_0=40, f_2=27, i=50-40=10 \\ \Delta_1=f_1-f_0 =41-40=1 \\ \Delta_2=f_1-f_2 =41-27=14
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =40+\frac{1}{1+14} \times 10 \\ =40+\frac{10}{15} \\ =40+\frac{2}{3} \\ =40+0.666 \\ Z \approx 40.67
समूहीकरण द्वारा

उपर्युक्त विश्लेषण से स्पष्ट है कि 40-50 वर्ग छह बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।अतः निरीक्षण और समूहीकरण दोनों से बहुलक समान है।
Z \approx 40.67
Example:57.निम्नलिखित समंकों से मध्यका,चतुर्थक,6वाँ दशमक व 76वाँ शतमक ज्ञात कीजिए:
(Calculate the Median,Quartiles,6th Deciles and 76th percentile from the following data):
![]()
Solution:Calculation Table of Median,Quartiles etc.

m=\frac{N}{2}=\frac{100}{2}=50
It falls in group 40-50
l_1=40, i=50-40=10, c=32, f=28
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =40+\frac{10}{28}(50-32) \\ =40+\frac{10}{28} \times 18 \\ =40+\frac{45}{7} \\ =40+6.4285 \\=46.4285 \\ \Rightarrow M \approx 46.43 \\ q_1=\frac{N}{4}=\frac{100}{4}=25
It falls in 30-40 group
l_1=30, i=40-30=10, c=20,f=12 \\ q_1=l_1+\frac{i}{f}\left(q_1-c\right) \\ =30+\frac{10}{12}(25-20) \\ =30+\frac{10}{72} \times 5 \\ =30+4.166 \\ =34.166 \\ \Rightarrow Q_{1} \approx 34.17 \\ q_3=\frac{3 N}{4}=\frac{3 \times 100}{4} =75
It falls in 50-60 group
l_1=50, i=60-50=10, c=60,f=20 \\ Q_3=l_1+\frac{i}{f}\left(q_3-c\right) \\ =50+\frac{10}{20}(75-60) \\ =30+\frac{10}{20} \times 15 \\ =50+7.5 \\ Q_3=57.5 \\ d_6=\frac{6 N}{10} \\ d_6=\frac{6 \times 100}{10}=60
It falls in 40-50 group
l_1=40, i=50-40=10, c=32, f=28 \\ D_6 =l_1+\frac{i}{f}\left(d_6-c\right) \\ =40+\frac{10}{28}(60-32) \\ =40+\frac{10}{28} \times 28 \\ =40+10 \\ \Rightarrow D_6 =50 \\ p_{76} =\frac{76 \mathrm{~N}}{100} \\ =\frac{76 \times 10}{100} \\ \Rightarrow p_{76}=76
It falls in 50-60 group
l_1=50, i=60-50=10, c=60, f=20 \\ P_{76}=l_1+\frac{i}{5}\left(P_{76}-c\right) \\ =50+\frac{10}{20}(76-60) \\ =50+\frac{1}{2} \times 16 \\ =50+8 \\ \Rightarrow P_{76} =58 \text { marks } \\ m= 46.43 Q1 \approx 34.17, Q_3 \approx 57.5, D_6=50, P_{76}=58
Example:58.निम्न सारणी एक विषय में 65 विद्यार्थियों द्वारा प्राप्तांकों को प्रदर्शित करती है।समान्तर माध्य,मध्यका,बहुलक तथा चतुर्थकों का परिकलन कीजिए:
(The following table gives the marks obtained by 65 students in a certain subject.Calculate Mean,Median,Mode and Quartiles):
![]()
Solution:Calculation Table of Mean,Median,Mode etc.
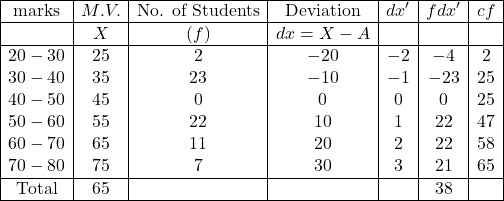
समान्तर माध्य (\overline{x}) =A+\frac{\sum f d x^{\prime}}{N} \times i \\ =45+\frac{38}{65} \times 10 \\ =45+\frac{380}{65} \\ =45+5.846 \\=50.8465 \\ \overline{x} \approx 50.85
मध्यका: m=\frac{N}{2}=\frac{65}{2}=32.5
It falls in 50-60 group
l_1=50, i=60-50=10, c=25, f=22
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =50+\frac{10}{22}(32.5-25) \\ =50+\frac{10 \times 7.5}{22} \\ =50+\frac{75}{22} \\ =50+3.409 \\ =53.409 \\ \Rightarrow M \approx 53.41
प्रथम चतुर्थक: q_1=\frac{N}{4}=\frac{65}{4} \\ \Rightarrow q_1=16.25
It falls in 30-40 group
l_1=30, i=40-30=10, f=23, c=2 \\ Q_1=l_1+\frac{i}{f}\left(q_1-c\right) \\ =30+\frac{10}{23}(16.25-2) \\ =30+\frac{10}{23}(14.25) \\ =30+\frac{142.5}{23} \\ =30+6.1956 \\ =36.1956 \\ Q_1 \approx 36.20
तृतीय चतुर्थक
q_3=\frac{3 N}{4}=\frac{3 \times 65}{4} \\ \Rightarrow q_3=48.75
It falls in 60-70 group
l_1=60, i=70-60=10,f=11, c=47 \\ Q_3=l_1+\frac{i}{f}\left(q_3-c\right) \\ =60+\frac{10}{11}(48.75-47) \\ =60+\frac{10}{11}(1.75) \\ =60+17.5 \\ =60+1.5909 \\ =61.5909 \\ \Rightarrow Q_3 \approx 61.59
बहुलक:
निरीक्षण द्वारा बहुलक वर्ग 30-40
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \\ =30+\frac{21 \times 10}{21+23} \\ =30+\frac{210}{44} \\ =30+4.772 \\ =34.772 \\ \Rightarrow Z \approx 34.77
समूहीकरण द्वारा

उपर्युक्त विश्लेषण से स्पष्ट है कि 50-60 वर्ग चार बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है अतः सूत्र द्वारा
f_1=22, f_0=0, f_2=11 \\ \Delta_1=f_1-f_0=22-0=22 \\ \Delta_2=f_1-f_2=2211=11 \\ l_1=50, i=60-50=10
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =50+\frac{22}{22+11} \times 10 \\ =50+\frac{220}{35} \\ =50+6.666 \\ =56.666 \\ \Rightarrow Z \approx 56.67 \\ \overline{Z} \approx 50.85, M \approx 53.41,Q_1=36.20,Q_{3} \approx 61.59 ,Z \approx 56.6
Example:59.निम्नलिखित सारणी से समान्तर माध्य तथा मध्यका ज्ञात कीजिए:
(From the following table calculate the Mean and Median):
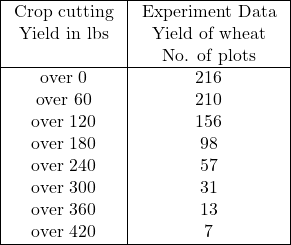
Solution:Calculation Table of Mean and Median

समान्तर माध्य (\overline{X})=A+\frac{\sum f d x^{\prime}}{N} \times i \\ =210+\frac{(-76)}{216} \times 60 \\ =210-\frac{4860}{216} \\ =210-21.16 \\ =188.889 \\ \Rightarrow \overline{X} \approx 188.89 \mathrm{lbs}
मध्यका: m=\frac{N}{2}=\frac{216}{2}=108
It falls in 120-180 group
l_1=120, i =180-120=60, f=58,c=60
मध्यका (M)=l_1+\frac{i}{8}(m-c) \\ =120+\frac{60}{58}(108-60) \\ =120+\frac{60}{58} \times 48 \\ =120+\frac{2880}{58} \\ =120+49.655 \\ =169.6551 \\ \Rightarrow M \approx 169.65 \mathrm{lbs}
Example:60.निम्नलिखित समंकों से समान्तर माध्य,मध्यका तथा बहुलक की गणना कीजिए:
(Calculate Mean,Median and Mode from the following data):
![]()
Solution:Calculation Table of Mean,Median and Mode

समान्तर माध्य (\overline{X})=A+\frac{\sum f d x}{N} \times i \\ =12.5-\frac{2}{35} \times 5 \\ =12.5-0.2857 \\ =12.2143 \\ \Rightarrow \overline{X} \approx 12.21
मध्यका: m=\frac{N}{2}=\frac{35}{2}=17.5
It falls in 10-15 group
l_1=10, i=15-10=5, c=13, f=10
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =10+\frac{5}{10}(17.5-13) \\ =10+\frac{1}{2} \times 4.5 \\ =10+2.25 \\ \Rightarrow M=12.25
बहुलक:निरीक्षण द्वारा बहुलक वर्ग 10-15
l_1=10, \quad i=15-10=5 \\ f_1=10, f_0=8, f_2=8 \\ \Delta_1=f_1-f_0=10-8=2 \\ \Delta_2=f_1-f_2=10-8=2
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =10+\frac{2}{2+2} \times 5 \\ =10+2.5 \\ \Rightarrow Z=12.5
समूहीकरण द्वारा

उपर्युक्त विश्लेषण से स्पष्ट है कि 10-15 वर्ग छह बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।अतः निरीक्षण और समूहीकरण दोनों से बहुलक समान है।
Z=12.5
उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में समान्तर माध्य और बहुलक (Arithmetic Mean and Mode in Statistics),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) को समझ सकते हैं।
3.सांख्यिकी में समान्तर माध्य और बहुलक की समस्याएँ (Arithmetic Mean and Mode in Statistics Problems):
(1.)निम्न सारणी संशोधन कीजिए और संशोधित सारणी से मध्यका-मूल्य ज्ञात कीजिए।
\begin{array}{|c|c|} \hline \text {मूल्य } & \text { आवृत्ति } \\ \hline 10-15 & 10 \\ \hline 15-17.5 & 15 \\ \hline 17.5-20 & 20 \\ \hline 22-30 & 25 \\ \hline 30-35 & 28 \\ \hline 35-40 & 30 \\ \hline \text{ 45 और अधिक } & 40 \\ \hline \end{array}
(2.)किसी कक्षा-परीक्षा में 20 विद्यार्थियों द्वारा प्राप्तांक निम्नांकित है।निम्नतर चतुर्थक (Lower Quartile),सातवाँ दशमक (7th Decile) और 82वाँ शतमक (82nd percentile) ज्ञात कीजिए।
\begin{array}{|cccccccccc|} \hline 18 & 10 & 4 & 31 & 25 & 20 & 24 & 17 & 35 & 15 \\ \hline 40 & 2 & 8 & 19 & 21 & 11 & 13 & 22 & 24 & 30 \\ \hline \end{array}
उत्तर (Answers): (1.)M=32.6 (2.) Q_1=11.5, D_7=24, P_{82}=30.22
उपर्युक्त सवालों को हल करने पर सांख्यिकी में समान्तर माध्य और बहुलक (Arithmetic Mean and Mode in Statistics),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) को ठीक से समझ सकते हैं।
Also Read This Article:- Mode and Median in Statistics
4.सांख्यिकी में समान्तर माध्य और बहुलक (Frequently Asked Questions Related to Arithmetic Mean and Mode in Statistics),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.समान्तर माध्य की प्रमुख उपयोगिता बताइए। (State the main use of mean):
उत्तर:सामाजिक तथा आर्थिक समस्याओं के अध्ययन हेतु अधिकांशतः इसी माध्य का प्रयोग किया जाता है।इस माध्य में एक आदर्श माध्य के लगभग सभी लक्षण विद्यमान हैं।यह माध्य सभी मूल्य पर आधारित होता है,स्पष्ट व निश्चित है,समझने व गणना में सरल है,प्रतिदर्श परिवर्तनों से अधिक प्रभावित नहीं होता है तथा इसका बीजगणितीय विवेचन संभव है।अतः इस माध्य का प्रयोग लगभग सभी स्थितियों में किया जाना उपयुक्त रहता है।इनका प्रयोग मात्र उन परिस्थितियों में नहीं किया जाना चाहिए जबकि विशेष प्रकार के माध्य के प्रयोग हेतु कोई विशेष कारण उपस्थित हों।औसत उत्पादन,औसत लागत,औसत आयात व निर्यात,औसत आय,औसत भार,औसत लंबाई आदि के अध्ययन हेतु इसी माध्य का प्रयोग करना चाहिए।जब आवृत्ति वितरण के आधार पर वक्र की संरचना करनी हो तो यही माध्य प्रयुक्त किया जाता है।
प्रश्न:2.मध्यका की प्रमुख उपयोगिता बताइए। (State the main use of median):
उत्तर:मध्यका का प्रयोग विशेषतः गुणात्मक प्रकृति के समंकों का सारांश ज्ञात करने हेतु किया जाता है; ईमानदारी,योग्यता,बौद्धिक स्तर,स्वास्थ्य आदि का अध्ययन करने हेतु मध्यका का प्रयोग उचित रहता है।इसका प्रयोग सामाजिक समस्याओं के अध्ययन में अधिक होता है।ऐसी स्थितियों में जहां अति-सीमान्त मदों को महत्त्व नहीं देना होता है,यह माध्य अधिक उपयुक्त रहता है।व्यापार के लिए इसका प्रयोग नहीं किया जाता क्योंकि व्यापारिक समंकों में स्थिरता नहीं होती है।
प्रश्न:3.बहुलक की प्रमुख उपयोगिता बताइए। (State the main use of mode):
उत्तर:यह माध्य प्रायः व्यापारिक,औद्योगिक एवं तकनीकी रीति-रिवाजों से संबंधित अध्ययनों में प्रयुक्त किया जाता है।एक व्यापारी द्वारा विक्रय हेतु माल का क्रय करते समय बहुलक आकार को ध्यान में रखना आवश्यक होगा।तैयार वस्त्रों (पोशाकों) का माध्य आकार, काॅलर का औसत आकार,जूतों का माध्य आकार,प्रति श्रमिक या प्रति मशीन औसत उत्पादन,परिवारों में औसत बच्चों की संख्या,टेलीफोन कॉल की औसत संख्या,प्रति संस्था औसत लाभ,मशीन का औसत उत्पादन समय,टोपी या हैट का औसत आकार,किसी पेड़ पर संतरों का औसत आकार आदि की जानकारी हेतु बहुलक ही प्रयुक्त किया जायेगा।जीव विज्ञान तथा अंतरिक्ष विज्ञान में भी बहुलक का प्रयोग निरंतर बढ़ता जा रहा है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में समान्तर माध्य और बहुलक (Arithmetic Mean and Mode in Statistics),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Arithmetic Mean and Mode in Statistics
सांख्यिकी में समान्तर माध्य और बहुलक
(Arithmetic Mean and Mode in Statistics)
Arithmetic Mean and Mode in Statistics
सांख्यिकी में समान्तर माध्य और बहुलक (Arithmetic Mean and Mode in Statistics) के इस
आर्टिकल में बहुलक,मध्यका और समान्तर माध्य से सम्बन्धित सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








