Median and Mean in Statistics
1.सांख्यिकी में मध्यका और माध्य (Median and Mean in Statistics),सांख्यिकी में दशमक और शतमक (Deciles and Percentiles in Statistics):
सांख्यिकी में मध्यका और माध्य (Median and Mean in Statistics) के अलावा इस आर्टिकल में चतुर्थकों,दशमक और शतमक पर आधारित उदाहरणों का भी अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Median in Statistics
2.सांख्यिकी में मध्यका और माध्य के उदाहरण (Median and Mean in Statistics Examples):
Example:28.निम्निलिखित समंकों से निम्न का परिकलन कीजिए:
Mean,Median (M), 7th Decile,and 85th Percentile

Solution:Calculation Table of Mean,Median,Decile and Percentile
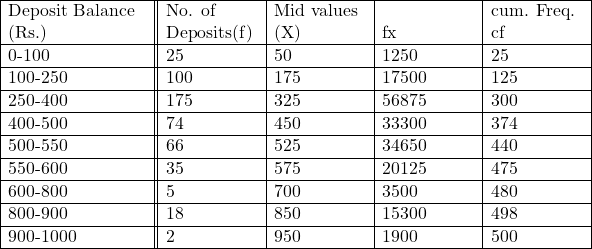
समान्तर माध्य (\overline{X}) =\frac{\sum f x}{N} \\ =\frac{184400}{500} \\ \Rightarrow \bar{X} =368.80 \\ m=\frac{N}{2}=\frac{500}{2}=250
यह मद संचयी आवृत्ति 300 में सम्मिलित है अतः मध्यका वर्ग 250-400 है।
l_{1}=250, c=125, i=400-250=150,f=175
मध्यका(M)=l_1+\frac{i}{f}(m-c) \\ =250+\frac{150}{175}(250-125) \\ =250+\frac{6}{7} \times+25 \\ =250+107.142 \\ =143357 .142 \\ \Rightarrow M \approx 357.14 \\ d_7=\frac{7 N}{10}=\frac{7 \times 500}{10}=350
It falls in 400-500 group
D_{7}=l_1+\frac{1}{f}\left(d_{7}-c\right) \\=400+\frac{100}{74}(350-300) \\ =400+\frac{100 \times 50}{74} \\ =400+67.567 \\ =467.567 \\ \Rightarrow D_9 \approx 467.57 \\ P_{85} =\frac{85 N}{100}=\frac{85 \times 500}{100} \\ \Rightarrow P_{85}=425[/katex]
It falls in 500-550 group
l_1=500, i=550-500=50, f=66, c=374 \\ P_{85} =l_1+\frac{i}{f}\left(p_{85}-c\right) \\ =500+\frac{50}{66}(425-374) \\=500+\frac{500}{66} \times 51 \\ =500+38.636 \\ =538.636 \\ \Rightarrow P_{85} \approx 538.64
Example:29.निम्नलिखित सारणी एक शहर की जनसंख्या का वितरण प्रदर्शित करती है।इन वितरणों से निम्न की गणना कीजिए:
(The following table shows the distribution of population of a city,calculate):
(i)Mean and Median (M)
(ii)Range of middle 50% items (मध्य 50% मदों की आयु का विस्तार)
(iii)Range of middle 80% items (मध्य 80% मदों की आयु का विस्तार)

Solution:Calculation Table of Mean,Median etc.

समान्तर माध्य (\overline{X})=\frac{\sum f x}{N} \\ =\frac{23181.25}{1000} \\=23.18125 \\ \Rightarrow \overline{X} \approx 23.18 \text { years } \\ m=\frac{N}{2}=\frac{1000}{2}=500
यह संचयी आवृत्ति 508 में सम्मिलित है अतः मध्यका वर्ग 9.5-19.5 है।
l_1=9.5, i=19.5-9.5=10, f=223, c=285
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\=9.5+\frac{10}{223}(500-285) \\ =9.5+\frac{10}{223} \times 215 \\ =9.5+9.641 \\ =19.141 \\ \Rightarrow M \approx 19.14
(ii)मध्य 50% मदों की आयु का विस्तार ज्ञात करने हेतु तृतीय व प्रथम चतुर्थक का अन्तर ज्ञात करना होगा:
q_1=\frac{N}{4}=\frac{1000}{4}=250
It falls in 0-9.5 group
l_1=0, i=9.5-0=9.5 ,f=285, i=0 \\ Q_1 =l_1+\frac{i}{f}\left(q_1-c\right) \\ =0+\frac{9.5}{285}(250-0) \\ =\frac{9.5}{285} \times 250 \\=8.333 \\ \Rightarrow Q_1 \approx 8.33 \\ q_3=\frac{3 N}{4}=\frac{3 \times 1000}{4}=750
It falls in 29.5-39.5 group
l_1=29.5, i=39.5-29.5=10, f=140, c=675 \\ Q_3 =l_i+\frac{i}{f}\left(q_3-c\right) \\ =29.5+\frac{10}{140}(750-675) \\ =29.5+\frac{1}{14} \times 75 \\ =29.5+5.3571 \\ =34.8571 \\ \Rightarrow Q_3 \approx 34.86 \\ Q_3-Q_1 =34.86-8.33=26.53 \text { years }
(iii)मध्य 80% मदों की आयु का विस्तार ज्ञात करने के लिए p_{90} व p_{10} का अन्तर ज्ञात करना होगा:
p_{90}=\frac{90 N}{100}=\frac{90 \times 1000}{100}=900
It falls in 39.5-49.5 group
l_1=39.5, c=49.5-39.5=10, f=91, c=81.5 \\ P_{90} =l_1+\frac{\dot{1}}{f}\left(P_{90}-c\right) \\ =39.5+\frac{10}{91}(900-815) \\ =39.5+\frac{10}{91} \times 85 \\ =39.5+9.3406 \\ =48.8406 \\ P_{90} \approx 48.84 \\ P_{10} =\frac{10 N}{100}=\frac{10 \times 1000}{100} \\ \Rightarrow P_{10} =100
It falls in 0-9.5 group
l_1=0, i=9.5-0=9.5, f=285, c=0 \\ P_{10}= l_1+\frac{i}{f}\left(P_{10}-c\right) \\ = \frac{9.5}{285}(100-0) \\ = \frac{9.5 \times 100}{285} \\ =3.333 \\ \Rightarrow P_{10} \approx 3.33 \\ P_{90}-P_{10}=48.84-3.33=45.51 \text { years }
Example:30.निम्नलिखित समंकों से समान्तर माध्य एवं मध्यका का परिकलन कीजिए:
(Calculate Arithmetic Mean and Median of the following data):

Solution:Calculation Table of Mean and Median

समान्तर माध्य पद विचलन रीति से (Mean by step deviation method):
\overline{X}=A+\frac{\Sigma fdx}{N} \times i \\ =35+\frac{46}{80} \times \\ =35+\frac{46}{8} \\=35+5.75 \\ \Rightarrow \overline{X}=40.75 \\ m=\frac{N}{2}=\frac{80}{2}=40
यह मद संचयी आवृत्ति 56 में सम्मिलित है अतः मध्यका वर्ग 40-50 है।
l_1=40, \bar{c} =50-40=10, f=19, c=37
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =40+\frac{10}{19}(40-37) \\ =40+\frac{10}{19} \times 3 \\ =40+\frac{30}{19} \\ =40+1.578 \\ =41.578 \\ \Rightarrow M \approx 41.58
Example:31.निम्नलिखित समंकों से मध्यका तथा समान्तर माध्य का परिकलन कीजिए:
(From the following data,calculate median and mean):
Solution:Calculation Table of Mean and Median

समान्तर माध्य लघुरीति से (Mean by Short-cut method):
\overline{X}=A+\frac{\sum f x}{N} \\ =45+\frac{(-880)}{200} \\ =45-4.4 \\ =40.6 \\ \Rightarrow \bar{X} =40.6 \text { manks } \\ m=\frac{N}{2}=\frac{200}{2}=100
यह संचयी आवृत्ति 104 में सम्मिलित है अतः मध्यका वर्ग 30-40 है।
l_1=30, i=40-30=10, f=28, c=76
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =30+\frac{10}{28}(100-76) \\ =30+\frac{10}{28} \times 24 \\ =30+\frac{60}{7} \\ =30+8.571 \\=38.571 \\ \Rightarrow M \approx 38.57
Example:32.निम्नलिखित श्रेणी से मध्यका व समान्तर माध्य प्राप्तांक ज्ञात कीजिए:
(From the following series, calculate median and mean marks):
Solution:Calculation Table of Mean and Median

समान्तर माध्य लघुरीति से (Mean by short-cut method):
\overline{X} =A+\frac{\sum f d x}{N} \\ =45+\frac{1100}{240} \\ =45+4.583 \\ =49.5 .83 \\ \overline{X} \approx 49.58 \\ m=\frac{N}{2}=\frac{240}{2}=120
यह मद संचयी आवृत्ति 125 में सम्मिलित है अतः मध्यका वर्ग 50-60 है।
l_1=50, i =60-50=10, f=30, c=95
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =50+\frac{10}{30}(120-95) \\ =50+\frac{1}{3} \times 25 \\ =50+8.333 \\ =58.333 \\ \Rightarrow M \approx 58.33
उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में मध्यका और माध्य (Median and Mean in Statistics),सांख्यिकी में दशमक और शतमक (Deciles and Percentiles in Statistics) को समझ सकते हैं।
3.सांख्यिकी में मध्यका और माध्य की समस्याएं (Median and Mean in Statistics Problems):
(1.)निम्न सारणी में किसी कारखाने के कर्मचारियों की दो वर्षों की आय दी गई है।सर्वोच्च 25% आय कमाने वाले प्रत्येक कर्मचारियों को 2% राष्ट्रीय सुरक्षा कोष में अंशदान देना है।1972 में 1971 की तुलना में अंशदान में कितनी वृद्धि हुई?
(The table below gives the income of the employees in a big factory for two years.Every employee belonging to the top 25 percent of the earners is required to pay 2 percent for the National Defence Fund.Find the increase in contributions to this fund from 1971 to 1972.)

(संकेत 25% आय कमाने वाले (150 और 200) 400 से 800 रुपए वाले आय वर्गों से है।उनकी कुल मासिक आय प्राप्त करके 12 से गुणा कर दिया जायेगा।इस वार्षिक आय पर 2% अंशदान निकाला जाएगा)
(2.)निम्न सारणी से मध्यका और बहुलक ज्ञात कीजिए:
(From the following table, find the median and the mode):

उत्तर (Answers):(1.) 1972 में वृद्धि=7464 रु.
(2.)M=12.15 days, Z=11.3 days
उपर्युक्त सवालों को हल करने पर सांख्यिकी में मध्यका और माध्य (Median and Mean in Statistics),सांख्यिकी में दशमक और शतमक (Deciles and Percentiles in Statistics) को ठीक से समझ सकते हैं।
Also Read This Article:-Arithmetic Average in Statistics
4.सांख्यिकी में मध्यका और माध्य (Frequently Asked Questions Related to Median and Mean in Statistics),सांख्यिकी में दशमक और शतमक (Deciles and Percentiles in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.मध्यका की विशेषताएं बताइए। (State characteristics of Median):
उत्तर:(1.)मध्यका एक स्थिति संबंधी माप है।
(2.)मध्यका के मूल्य पर अतिसीमान्त इकाइयों (extreme items) का प्रभाव बहुत कम होता है।
(3.)मध्यका की गणना उस दशा में की जा सकती है जब श्रेणी की मदों को संख्यात्मक रूप नहीं दिया जा सकता हो।
(4.)अन्य माध्यों की भाँति मध्यका का गणितीय विवेचन संभव नहीं है।
(5.)यदि मदों की संख्या व मध्यका वर्ग मात्र के विषय में सूचना दी हुई हो तो भी मध्यका की गणना संभव है अर्थात् अपूर्ण सूचना से भी मध्यका मूल्य का निर्धारण संभव है।
प्रश्न:2.मध्यका के गुणों को बताइए। (State properties of Median):
उत्तर:(1.)बुद्धिमत्ता,सुंदरता एवं स्वच्छता आदि गुणात्मक विशेषताओं के अध्ययन के लिए अन्य माध्यों की अपेक्षा मध्यका श्रेष्ठ समझा जाता है।
(2.)मध्यका पर अति-सीमांत और साधारण मदों का प्रभाव नहीं पड़ता है।
(3.)मध्यका ज्ञात करना सरल व सुविधाजनक रहता है।इसकी गणना करना एक साधारण व्यक्ति भी सरलता से समझ सकता है।
(4.)कभी-कभी तो मध्यका की गणना निरीक्षण मात्र से ही की जा सकती है।
(5.)मध्यका को बिंदु रेखीय पद्धति से भी ज्ञात किया जा सकता है।
(6.)मध्यका की गणना करने के लिए संपूर्ण समंकों की आवश्यकता नहीं होती है।केवल मदों की संख्या व मध्यका वर्ग का ज्ञान पर्याप्त है।
(7.)यदि आवृत्तियों की प्रवृत्ति श्रेणी के मध्य समान रूप से वितरित होने की हो तो मध्यका को एक विश्वसनीय माध्य माना जाता है।
(8.)मध्यका सदैव निश्चित एवं स्पष्ट होता है व सदैव ज्ञात किया जा सकता है।
(9.)मध्यका अधिकतर श्रेणी में दिए गए किसी मूल्य के समान नहीं होता है।
प्रश्न:3.मध्यका के सिद्धान्त पर आधारित अन्य माप कौन-कौनसी हैं? (What are the other measures based on principle of median?):
उत्तर:जिस प्रकार मध्यका द्वारा एक श्रेणी को अनुविन्यसित मदों को दो बराबर भागों में बांटा जाता है,उसी प्रकार श्रेणी को चार,पांच,आठ,दस व सौ बराबर भागों में बांटा जा सकता है।चार बराबर भागों में बांटने वाला मूल्य चतुर्थक (Quartiles),पांच भागों में बांटने वाला मूल्य पंचमक (Quintiles),आठ भागों में बांटने वाला मूल्य अष्टमक (Octiles),दस वाले दशमक (Deciles) व सौ बराबर भागों में बांटने वाले मूल्य शतमक (Percentiles) कहलाते हैं।इन विभिन्न मापों का प्रयोग सांख्यिकीय विश्लेषण में किया जाता है।यह माप अपनी स्थिति के आधार पर निर्धारित की जाती है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में मध्यका और माध्य (Median and Mean in Statistics),सांख्यिकी में दशमक और शतमक (Deciles and Percentiles in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Median and Mean in Statistics
सांख्यिकी में मध्यका और माध्य
(Median and Mean in Statistics)
Median and Mean in Statistics
सांख्यिकी में मध्यका और माध्य (Median and Mean in Statistics) के अलावा इस आर्टिकल
में चतुर्थकों,दशमक और शतमक पर आधारित उदाहरणों का भी अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








