Area of Parallelograms Class 9
1.समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms Class 9),त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9):
समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms Class 9) के इस आर्टिकल में एक ही आधार और एक ही समान्तर रेखाओं के बीच बने समान्तर चतुर्भुजों व त्रिभुजों के क्षेत्रफल का अध्ययन करेंगे।
प्रमेय (Theorem):9.1.एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
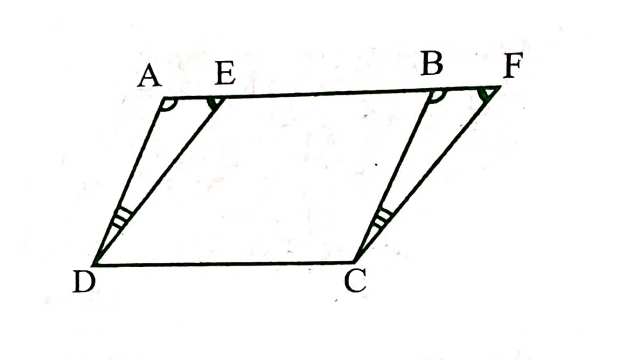
दिया है (Given):दो समान्तर चतुर्भुज ABCD और EFCD जो एक ही आधार DC और एक ही समान्तर रेखाओं AF और DC के बीच स्थित है।
सिद्ध करना है (To Prove): ar(ABCD)=ar(EFCD)
उपपत्ति (Proof): \triangle ADE और \triangle BCF में
\angle DAE=\angle CBF (AD \parallel BC और तिर्यक AF से संगत कोण)… (1)
\angle AED=\angle BFC ( ED \parallel FC और तिर्यक रेखा AF से संगत कोण)…. (2)
\angle ADE=\angle BCF (त्रिभुज कोण योग युग्म)…. (3)
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएँ)……….(4)
(ASA सर्वांगसमता नियम तथा (1),(3) और (4) द्वारा)
\triangle ADE \cong \triangle BCF
ar(ADE)=ar(BCF) (सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं)….. (5)
ar(ABCD)=ar(ADE)+ar(EDCB)
=ar(BCF)+ar(EDCB)[(5) से ]
\Rightarrow ar(ABCD)=ar(EFCD)
अतः समान्तर चतुर्भुज ABCD और EFCD क्षेत्रफल में बराबर होते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Area of Parallelograms and Triangles
2.समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 के साधित उदाहरण (Area of Parallelograms Class 9 Solved Examples):
Example:1.आकृति में,ABCD एक समान्तर चतुर्भुज है AE \perp DC और CF \perp AD है।यदि AB=16cm,AE=8cm और CF=10cm है तो AD ज्ञात कीजिए।
Solution:समान्तर चतुर्भुज ABCD का क्षेत्रफल जब आधार DC हो=आधार × ऊँचाई
=DC×AE
=16×8 [DC=AB]
समान्तर चतुर्भुज का क्षेत्रफल जब आधार AD हो=AD×CF
=AD×10
(1) व (2) सेः AD \times 10=16 \times 8 \\ \Rightarrow A D=\frac{16 \times 8}{10}=\frac{128}{10} \\ \Rightarrow AD=12.8 सेमी
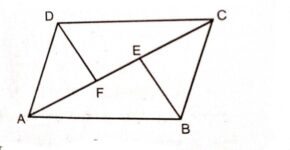
Example:2.यदि E,F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य बिन्दु हैं तो दर्शाइए कि \operatorname{ar}(EFGH)=\frac{1}{2} \operatorname{ar}(ABCD) है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD की भुजाओं AB,BC,CD,DA के मध्य बिन्दु क्रमशः E,F,G तथा H है।
सिद्ध करना है (To Prove): \operatorname{ar}(EFGH)=\frac{1}{2} \operatorname{ar}(ABCD)
उपपत्ति (Proof): \triangle HGF और समान्तर चतुर्भुज HDCF एक ही आधार HF और एक ही समान्तर भुजाओं HF और DC के मध्य स्थित हैं।
\operatorname{ar}(HGF)=\frac{1}{2} \operatorname{ar}(HDCF) \cdots(1)
इसी प्रकार \triangle HEF और समान्तर चतुर्भुज ABFH एक ही आधार HF और एक ही समान्तर रेखाओं HF और AB के मध्य स्थित हैं।
\operatorname{ar}(HEF)=\frac{1}{2} \operatorname{ar}(ABFH) \cdots(2)
(1) व (2) को जोड़ने परः
\operatorname{ar}(HGF)+\operatorname{ar}(HEF)=\frac{1}{2} \operatorname{ar}(HDCF)+\frac{1}{2} \operatorname{ar}(ABFH) \\ \Rightarrow \operatorname{ar}(EFGH)=\frac{1}{2} \operatorname{ar}(ABCD)
Example:3. P और Q क्रमश समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित हैं।दर्शाइए कि ar(APB)=ar(BQC) है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर क्रमशः बिन्दु P व Q है।
सिद्ध करना है (To Prove): ar(APB)=ar(BQC)
उपपत्ति (Proof): \triangle APB और समान्तर चतुर्भुज ABCD एक ही आधार AB और एक ही समान्तर भुजाओं AB और DC पर स्थित हैं।
\because ar(APB)=\frac{1}{2} ar(ABCD) \cdots(1)
इसी प्रकार \triangle BQC और समान्तर चतुर्भुज ABCD एक ही आधार BC और एक ही समान्तर रेखाओं BC और AD के मध्य स्थित हैं।
\therefore \because ar(BQC)=\frac{1}{2} ar(ABCD) \cdots(2)
समीकरण (1) व (2) से
ar(APB)=ar(BQC)
Example:4.आकृति में, P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिन्दु है।दर्शाइए कि
(i)ar(APB)+ar(PCD)=\frac{1}{2} ar(ABCD)
(ii)ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
Solution:दिया है (Given):P समान्तर चतुर्भुज ABCD के अभ्यन्तर कोई बिन्दु है।
सिद्ध करना है (To Prove):
(i)ar(APB)+ar(PCD)=\frac{1}{2} ar(ABCD)
(ii)ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
रचना (Construction):EPF रेखा AB या DC के समान्तर खींची और GPH को AD और BC के समान्तर खींची।
उपपत्ति (Proof):अब AGHD समान्तर चतुर्भुज है
[ \because GH \parallel DA और AG \parallel DH ]
इसी प्रकार HCBG,EFCD तथा ABEF समान्तर चतुर्भुज हैं।
(i) \triangle APB और समान्तर चतुर्भुज ABFE एक ही आधार AB पर और एक ही समान्तर रेखाओं AB और CD के मध्य स्थित हैं।
\therefore ar(APB)=\frac{1}{2} ar(ABFE) ……..(1)
इसी प्रकार ar(PCD)=\frac{1}{2} ar(EFCD) …………(2)
समीकरण (1) व (2) को जोड़ने परः
ar(APB)+ar(PCD)=\frac{1}{2} ar(ABFE)+\frac{1}{2} ar(EFCD) \\ \Rightarrow ar(APB)+ar(PCD)=\frac{1}{2} ar(ABCD)
(ii) \triangle APD और समान्तर चतुर्भुज AGHD एक ही आधार AD पर और एक ही समान्तर रेखाओं AD और HG के मध्य स्थित हैं।
\therefore ar(APD)=\frac{1}{2} ar(AGHD) \cdots(4)
इसी प्रकार ar(PCB)=\frac{1}{2} ar(GBCH) \cdots(5)
समीकरण (4) व (5) को जोड़ने परः
ar(APD)+ar(PCB)=\frac{1}{2}\left[ ar(AGHD)+ar(GBCH) \right] \\ \Rightarrow ar(APD)+ ar(PCB)=\frac{1}{2} ar(ABCD) \cdots(6)
समीकरण (3) व (6) सेः
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
Example:5.आकृति में PQRS और ABRS समान्तर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिन्दु है।दर्शाइए कि
((i)ar(PQRS)=ar(ABRS)
(ii) ar(AXS)=\frac{1}{2} ar(PQRS)
Solution:दिया है (Given):दो समान्तर चतुर्भुज PQRS और ABRS हैं और भुजा BR पर एक बिन्दु X स्थित है।
सिद्ध करना है (To Prove):(i)ar(PQRS)=ar(ABRS)
(ii) ar(AXS)=\frac{1}{2} ar(PQRS)
उपपत्ति (Proof):(i)समान्तर चतुर्भुज PQRS और ABRS एक ही आधार SR और एक ही समान्तर रेखाओं SR और PB के बीच स्थित हैं।
\therefore ar(PQRS)=ar(ABRS)……….(1)
(ii) \triangle AXS और समान्तर चतुर्भुज ABRS एक ही आधार AS और एक ही समान्तर रेखाओं AS और RB के बीच स्थित हैं।
\therefore ar(AXS)=\frac{1}{2} ar(ABRS)
(1) व (2) सेः
ar(AXS)=\frac{1}{2} ar(PQRS)
Example:6.एक किसान के पास समान्तर चतुर्भुज PQRS के रूप का खेत था।उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया।खेत कितने भागों में विभाजित हो गया? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग अलग बोना चाहती है।वह ऐसा कैसे करे?
Solution:एक समान्तर चतुर्भुज PQRS की भुजा SR पर एक बिन्दु A स्थित है।A को P और Q से मिलाया गया है।
क्षेत्र को तीन भागों (i) \triangle ASP (ii) \triangle APQ (iii) \triangle AQR में बाँटा गया है।सभी भाग त्रिभुज हैं।
\triangle APQ और समान्तर चतुर्भुज PQRS एक ही आधार PQ और एक ही समान्तर रेखाओं के बीच स्थित हैं।
ar(APQ)=\frac{1}{2} ar(PQRS) \cdots(1) \\ \therefore ar(ASP)+ar(APQ)+ar(AQR)=ar(PQRS) \\ \Rightarrow ar(ASP)+ar(AQR)=\frac{1}{2} ar(PQRS) \cdots(2)
(1) व (2) सेः
ar(APQ)=ar(ASP)+ar(AQR)
अतः किसान को \triangle APQ में गेहूं \triangle ASP और \triangle AQR अन्य दो त्रिभुजों व में दालें बोनी चाहिए।
उपर्युक्त उदाहरणों के द्वारा समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms Class 9),त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9) को समझ सकते हैं।
3.समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 पर आधारित सवाल (Questions Based on Area of Parallelograms Class 9):
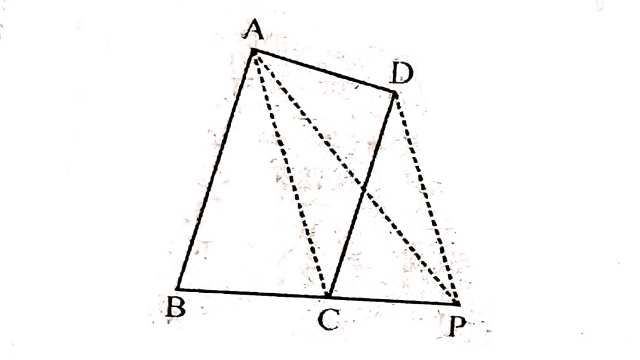
(1.)ABCD एक समान्तर चतुर्भुज है।D से होकर AC के समान्तर खींची गई एक रेखा खींची गई है जो BC को बढ़ाने पर P पर मिलती है।सिद्ध कीजिए किः
ar(\triangle ABP)=ar(चतुर्भुज ABCD)
(2.)एक समान्तर चतुर्भुज ABCD की एक भुजा AB को P तक बढ़ाया गया है।A से होकर एक रेखा CP के समान्तर खींची गई है जो CB को बढ़ाने पर Q पर मिलती है और समान्तर चतुर्भुज PBQR बनता है, जैसा कि आकृति में दर्शाया गया है।सिद्ध कीजिए किः
ar(समान्तर चतुर्भुज ABCD)=ar(समान्तर चतुर्भुज BPRQ)
उपर्युक्त सवालों को हल करने पर समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms Class 9),त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Mid-Point Theorem Class 9
4.समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Frequently Asked Questions Related to Area of Parallelograms Class 9),त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिभुज के क्षेत्रफल से क्या तात्पर्य है? (What Do You Mean by Area of a Triangle?):
उत्तर:(1.)तल के उस भाग को जो त्रिभुज से घिरा है,त्रिभुज का अभ्यन्तर (interior of a triangle) कहते हैं।
(2.)त्रिभुज और त्रिभुज के अभ्यन्तर के सम्मिलन को त्रिभुजाकार प्रदेश (Triangular region) कहते हैं।
(3.)इस प्रकार त्रिभुज के क्षेत्रफल से हमारा अभिप्राय त्रिभुजाकार प्रदेश के परिमाण से है।
प्रश्न:2.बहुभुज क्षेत्रफल से क्या अभिप्राय है? (What Do You Mean by Area of a Polygon?):
उत्तर:(1.)आयत के क्षेत्रफल से अभिप्राय आयत और आयत के अभ्यन्तर सम्मिलन अर्थात् आयताकार प्रदेश के परिमाण से है।
(2.)इसी प्रकार किसी बहुभुज के क्षेत्रफल से अभिप्राय उस बहुभुज और उसके अभ्यन्तर के सम्मिलन अर्थात् बहुभुज प्रदेश का परिणाम है।
प्रश्न:3.क्षेत्रफल अभिगृहीत क्या है? (What is Area Axiom?):
उत्तर:प्रत्येक बहुभुज का क्षेत्रफल होता है।एक मीटर भुजा वाला एक मानक वर्गाकार प्रदेश होता है जिसे वर्ग मीटर कहते हैं और जिसे क्षेत्रफल की इकाई मानते हैं।बहुभुज प्रदेश का क्षेत्रफल,वर्गमीटरों में,एक धन वास्तविक संख्या होती है।बहुभुज प्रदेश R के क्षेत्रफल को ar(R) से प्रकट करते हैं।यदि ar(R) वर्गमीटर में x हो तो हम लिखेंगे ar(R)=x \text{मी}^{2} वर्गमीटर
उपर्युक्त प्रश्नों के उत्तर द्वारा समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms Class 9),त्रिभुजों के क्षेत्रफल कक्षा 9 (Area of Triangles Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Area of Parallelograms Class 9
समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9
(Area of Parallelograms Class 9)
Area of Parallelograms Class 9
समान्तर चतुर्भुजों के क्षेत्रफल कक्षा 9 (Area of Parallelograms Class 9) के इस आर्टिकल
में एक ही आधार और एक ही समान्तर रेखाओं के बीच बने समान्तर चतुर्भुजों व त्रिभुजों
के क्षेत्रफल का अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.