Congruence of Triangles Class 9
1.त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9),कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9):
त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9) के इस आर्टिकल में भुजा-भुजा-भुजा सर्वांगसमता नियम,समकोण-कर्ण-भुजा सर्वांगसमता नियम का अध्ययन करेंगे।एक त्रिभुज की तीनों भुजाओं के बराबर होने पर त्रिभुज सर्वांगसम हो जाते हैं।
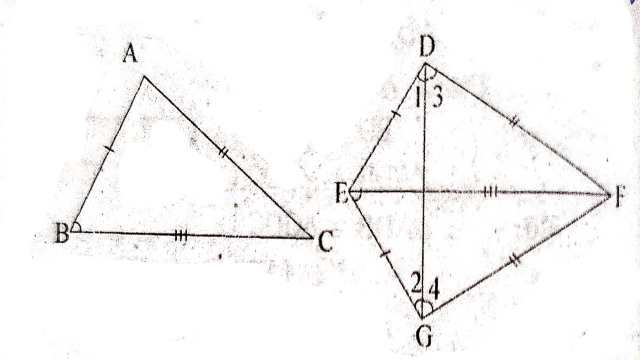
प्रमेय (Theorem):7.4.(SSS सर्वांगसमता नियम):यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं।
दिया है (Given): \triangle ABC \text { और } \triangle DEF में AB=DE,BC=EF और AC=DF
सिद्ध करना है (To Prove): \triangle ABC \cong \triangle DEF
रचना (Construction):माना BC सबसे बड़ी भुजा है | EG की रचना इस प्रकार की कि: EG=AB और \angle FEG=\angle CBA,GF और DF को मिलाया
उपपत्ति (Proof): \triangle ABC और \triangle GEF में
AB=GE (रचना द्वारा)
\angle ABC=\angle GEF (रचना द्वारा)
\therefore \triangle ABC \cong \triangle GEF (ASA सर्वांगसमता से)
इसलिए \angle A=\angle G \ldots(1) (CPCT)
AC=GF …. (2) (CPCT)
अब AB=EG (रचना से)
AB=DE (दिया है)
\therefore DE=EG …. (3)
इसी प्रकार DF=GF …. (4)
\triangle EDG में, DE=EG [(3) से]
\therefore \angle 1=\angle 2 \ldots(5)
(त्रिभुज की समान भुजाओं के सम्मुख कोण)
पुनः \triangle DFG में, DF=GF [(4) से]
\angle 3=\angle 4 \ldots(6)
(त्रिभुज की समान भुजाओं के सम्मुख कोण)
(5) और (6) को जोड़ने पर,
\angle 1+\angle 3=\angle 2+\angle 4 \\ \therefore \angle D=\angle G
परन्तु \angle G=\angle A ………[(1) से]
\therefore \angle A=\angle D \ldots(7)
AC=DF (दिया है)
इस प्रकार \triangle ABC \cong \triangle DEF (ASA सर्वांगसमता से)
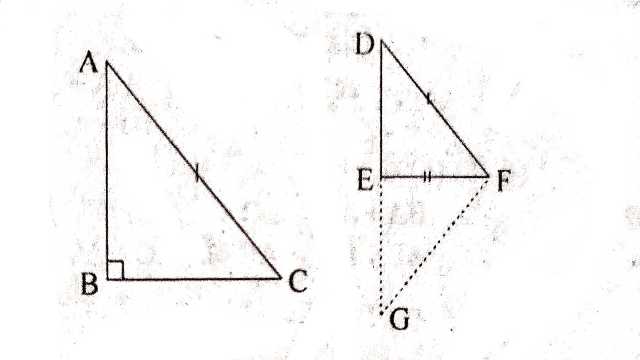
प्रमेय (Theorem):7.5.(RHS सर्वांगसमता नियम):यदि दो समकोण त्रिभुजों में,एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं।
दिया है (Given): \triangle ABC और \triangle DEF में
\angle B=\angle E=90^{\circ}
AC=DF
और BC=EF
सिद्ध करना है (To Prove): \triangle ABC \cong \triangle DEF
रचना (Construction):DE को G तक इस प्रकार बढ़ाया कि EG=AB,GF को मिलाया।
उपपत्ति (Proof): \triangle ABC \text { और } \triangle GEF में
AB=GE (रचना से)
\because \angle B=\angle GEF (प्रत्येक कोण 90°)
BC=EF (दिया है)
\therefore \triangle ABC \cong \triangle GEF (SAS सर्वांगसमता से)
\Rightarrow \angle A=\angle G (CPCT)…. (1)
और AC=GF (CPCT)…. (2)
\therefore AC=DF (दिया है)
परन्तु DF=GF
\Rightarrow \angle D=\angle G (त्रिभुज की समान भुजाओं के सम्मुख कोण)… (3)
(1) और (3) सेः
\angle A=\angle D \ldots(4) \\ \triangle ABC \text { और } \triangle DEF में
\angle A=\angle D [(4) से]
\angle B=\angle E (दिया है)
\therefore \angle C=\angle F (जब त्रिभुज के दो कोण समान होते हैं तो तीसरा कोण समान होता है)
पुनः \triangle ABC \text { और } \triangle DEF में
BC=EF (दिया है)
\because \angle C=\angle F [(5) से]
AC=DF (दिया है)
\therefore \triangle ABC \cong \triangle DEF (SAS सर्वांगसमता से)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Some Properties of Triangle Class 9
2.त्रिभुजों की सर्वांगसमता कक्षा 9 के साधित उदाहरण (Congruence of Triangles Class 9 Solved Examples):
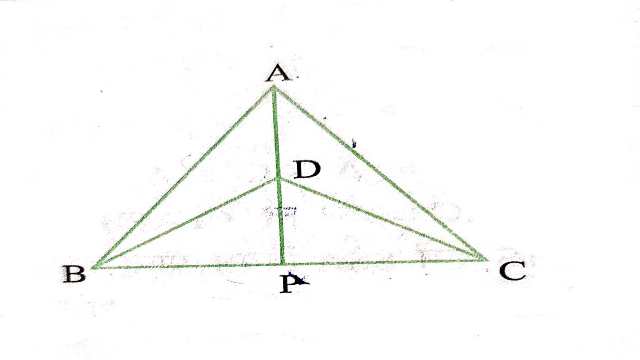
Example:1.\triangle ABC \text { और } \triangle DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)।यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे तो दर्शाइए कि
(i) \triangle ABD \cong \triangle ACD
(ii) \triangle ABP=\triangle ACP
(iii)AP , \angle A और \angle D दोनों को समद्विभाजित करता है।
(iv)AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
Solution:दिया है (Given): \triangle ABC \text { और } \triangle DBC दो समद्विबाहु त्रिभुज हैं जिनका उभयनिष्ठ आधार BC है जबकि शीर्ष A तथा D आधार के एक ही ओर स्थित हैं।
सिद्ध करना है (To Prove): (i) \triangle ABD \cong \triangle ACD
(ii) \triangle ABP=\triangle ACP
(iii)AP , \angle A और \angle D दोनों को समद्विभाजित करता है।
(iv)AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
उपपत्ति (Proof): \triangle ABC तथा \triangle DBC समद्विबाहु त्रिभुज हैं अतः
AB=AC तथा BD=DC …. (1)
(i) \triangle ABD और \triangle ACD में
AB=AC (दिया है) [(1) से]
BD=CD [(1) से]
AD=AD (उभयनिष्ठ है)
\therefore \triangle ABD \cong \triangle ACD (SSS सर्वांगसमता नियम से)
(ii) \because \angle BAD=\angle CAD (CPCT) \\ \Rightarrow \angle BAP=\angle CAP \\ \therefore \angle A को AD या AP समद्विभाजित करता है।
\triangle ABP और \triangle ACP में
\angle BAP=\angle CAP (सिद्ध किया है)
AB=AC (दिया है) [(1) से]
AP=AP (उभयनिष्ठ है)
\therefore \triangle ABP \cong \triangle ACP (SAS सर्वांगसमता नियम से)
(iii) \therefore \angle APB=\angle APC (CPCT)
परन्तु \angle APB+\angle APC=180^{\circ} (रैखिक कोण युग्म)
\therefore \angle APB=समकोण
\therefore AP \perp BC \\ \therefore BP=PC (CPCT)
अतः AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
(iii) \triangle BPD तथा \triangle CPD में
BP=PC (सिद्ध किया है)
\angle BPD=\angle CPD=90^{\circ}(सिद्ध किया है)
PD=PD (उभयनिष्ठ है)
\triangle BPD \cong \triangle CPD (SAS सर्वांगसमता नियम से)
\therefore \angle BDP=\angle CDP (CPCT से)
अतः AP समद्विभाजक है \angle A और \angle D का।
Example:2.AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है जिसमें AB=AC है।दर्शाइए कि
(i)AD रेखाखण्ड BC को समद्विभाजित करता है।
(ii)AD कोण A को समद्विभाजित करता है।
Solution:दिया है (Given):समद्विबाहु \triangle ABC में AB=AC तथा AD \perp BC
सिद्ध करना है (To Prove):(i)AD रेखाखण्ड BC को समद्विभाजित करता है।
(ii)AD कोण A को समद्विभाजित करता है।
उपपत्ति (Proof):(i) \triangle ADB तथा \triangle ADC में
AB=AC (दिया है)
AD=AD (उभयनिष्ठ है)
\angle ADB=\angle ADC=90^{\circ} (दिया है)
अतः \triangle ADB \cong \triangle ADC (समकोण-कर्ण-भुजा सर्वांगसमता से)
BD=DC (CPCT)
अतः AD, रेखाखण्ड BC को समद्विभाजित करता है।
(ii) \triangle ADB \cong \triangle ADC (सिद्ध किया है)
\angle BAD=\angle CAD (CPCT)
अतः AD, \angle A को समद्विभाजित करता है।
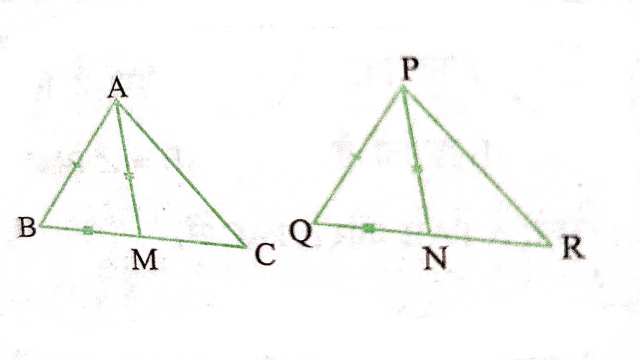
Example:3.एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक दूसरे त्रिभुज की भुजाओं PQ और QR तथा माध्यिका PN के बराबर है (देखिए आकृति)।दर्शाइए कि
(i) \triangle ABM \cong \triangle PQN
(ii) \triangle ABC \cong \triangle PQR
Solution:(i)BC=QR
\Rightarrow \frac{1}{2} BC=\frac{1}{2} QR \\ \Rightarrow BM=QN (AM व PN माध्यिका है)… (1)
\triangle ABM \text { तथा } \triangle PQN में
AB=PQ (दिया है)
BM=QN [(1) से]
AM=PN (दिया है)
\triangle ABM \cong \triangle PQN (SSS सर्वांगसमता नियम से)
(ii)\triangle ABM \cong \triangle PQN (सिद्ध किया है)
\angle B=\angle Q (CPCT से)……(2)
\triangle ABC \text { तथा } \triangle PQR में
AB=PQ (दिया है)
\angle B=\angle Q [(2) से]
BC=QR (दिया है)
\triangle ABC \cong \triangle PQR (SAS सर्वांगसमता से)
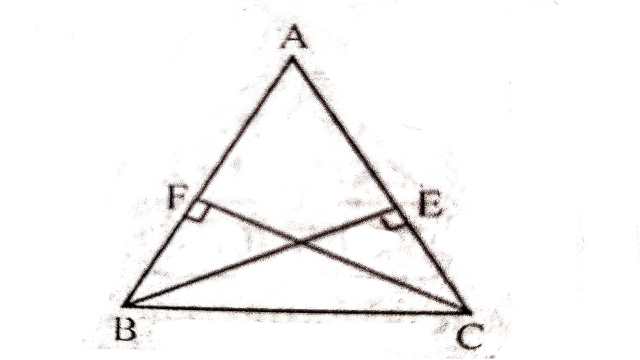
Example:4.BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं।RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज है।
Solution:दिया है (Given): \triangle ABC में BE और CF दो बराबर शीर्षलम्ब हैं।
सिद्ध करना है (To Prove):\triangle ABC समद्विबाहु त्रिभुज है।
उपपत्ति (Proof): \triangle BEC तथा \triangle CFB में
BE=CF (दिया है)
BC=BC (उभयनिष्ठ है)
\angle BEC=\angle CFB=90^{\circ} \\ \triangle BEC \cong \triangle CFB (समकोण-कर्ण-भुजा सर्वांगसमता से)
\angle BCE=\angle CBF (CPCT से)
AB=AC (त्रिभुज के बराबर कोण की सम्मुख भुजाएँ)
\triangle ABC समद्विबाहु त्रिभुज है।
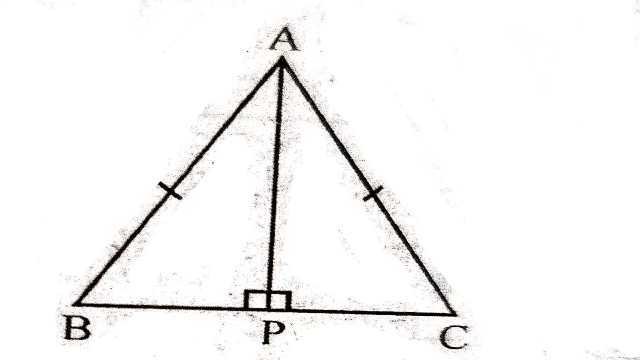
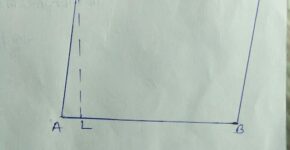
Example:5.ABC एक समद्विबाहु त्रिभुज है जिसमें AB=AC है। AP \perp BC खींचकर दर्शाइए कि \angle B=\angle C है।
Solution:दिया है (Given): \triangle ABC समद्विबाहु त्रिभुज है जिसमें AB=AC है।
सिद्ध करना है (To Prove): \angle B=\angle C
रचना (Construction):A से AP \perp BC खींचा।
उपपत्ति (Proof): \triangle APB तथा \triangle APC में
AB=AC (दिया है)
AP=AP (उभयनिष्ठ है)
\angle APB=\angle APC=90^{\circ} (दिया है)
\therefore \triangle APB \cong \triangle APC (समकोण-कर्ण-भुजा सर्वांगसमता से)
\angle ABP=\angle ACP (CPCT से)
\Rightarrow \angle B=\angle C
उपर्युक्त उदाहरणों के द्वारा त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9),कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9) को समझ सकते हैं।
3.त्रिभुजों की सर्वांगसमता कक्षा 9 के सवाल (Congruence of Triangles Class 9 Questions):
(1.)दो समकोण त्रिभुजों ABC तथा DEF में विकर्ण AC=विकर्ण EF तथा AB=DE यदि \angle A=30^{\circ} तथा \angle C=60^{\circ} तो \angle E का मान लिखिए।
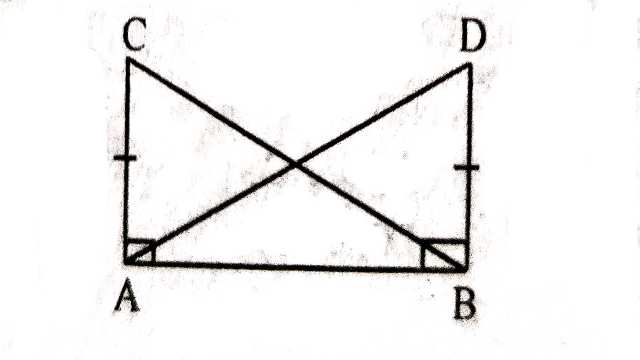
(2.)चित्र में AC=BD, CA \perp AB और DB \perp AB कौनसे त्रिभुज परस्पर सर्वांगसम हैं? उन्हें सांकेतिक रूप में लिखिए।
उत्तर (Answers):(1) \angle E=30^{\circ}
(2) \triangle BAC \cong \triangle ABD
उपर्युक्त सवालों को हल करने पर त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9),कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Triangle Class 9
4.त्रिभुजों की सर्वांगसमता कक्षा 9 (Frequently Asked Questions Related to Congruence of Triangles Class 9),कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिभुजों की सर्वांगसमता के कौन-कौनसे गुणधर्म हैं? (What are the Properties of the Congruence of Triangles?):
उत्तर:(1.)SSS सर्वांगसमता नियम
(2.)SAS सर्वांगसमता नियम
(3.)ASA सर्वांगसमता नियम
(4.)RHS सर्वांगसमता नियम
प्रश्न:2.सर्वांगसमता से क्या तात्पर्य है? (What Do You Mean by Congruence?):
उत्तरःसर्वांगसम का अर्थ है ‘सभी प्रकार से समान’ अर्थात् वे आकृतियाँ जिनका आकार और माप समान हो।
प्रश्न:3.त्रिभुज की सर्वांगसमता की मुख्य बातें लिखिए। (Write Down HIGHLIGHTS of Congruence of Triangles):
उत्तर:(1.)समान त्रिज्याओं वाले दो वृत्त सर्वांगसम होते हैं।
(2.)समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।
(3.)यदि \triangle ABC और \triangle PQR संगतता A \leftrightarrow P, B \leftrightarrow Q और C \leftrightarrow R के अन्तर्गत सर्वांगसम हों तो उन्हें सांकेतिक रूप में \triangle ABC \cong \triangle PQR लिखते हैं।
(4.)यदि एक त्रिभुज की दो भुजाएँ और उनके अन्तर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अन्तर्गत कोण के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।
(5.)यदि एक त्रिभुज के दो कोण और अन्तर्गत भुजा दूसरे त्रिभुज के दो कोणों और अन्तर्गत भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।
(6.)यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।
(7.)त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
(8.)त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
(9.)यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों भुजाओं के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (SSS सर्वांगसमता नियम)।
(10.)यदि दो समकोण त्रिभुजों में एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (RHS सर्वांगसमता नियम)।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9),कक्षा 9 में त्रिभुजों की सर्वांगसमता (Congruence of Triangles in Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Congruence of Triangles Class 9
त्रिभुजों की सर्वांगसमता कक्षा 9
(Congruence of Triangles Class 9)
Congruence of Triangles Class 9
त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9) के इस आर्टिकल में
भुजा-भुजा-भुजा सर्वांगसमता नियम,समकोण-कर्ण-भुजा सर्वांगसमता नियम का अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.