area of quadrilateral in hindi
चतुर्भुज का क्षेत्रफल (Area of Quadrilateral):
- चतुर्भुज का क्षेत्रफल (Area of Quadrilateral):चार भुजाओं से घिरी हुई आकृति चतुर्भुज कहलाती है। किसी चतुर्भुज को उसके विकर्णों द्वारा दो त्रिभुजों में विभाजित किया जा सकता है। चित्रानुसार चतुर्भुज ABCD को विकर्ण AC दो त्रिभुजों ABC एवं ACD त्रिभुज में विभक्त करता है। अतः चतुर्भुज ABCD का क्षेत्रफल दोनों त्रिभुजों के क्षेत्रफलों के योग के बराबर होगा।
- चतुर्भुज के शीर्ष B एवं D से विकर्ण AC पर लम्ब क्रमशः BE एवं DF खींचिए।
अतः त्रिभुज ABC का क्षेत्रफल=\frac{1}{2}×\text{AC×BE}
अतः त्रिभुज ACD का क्षेत्रफल=\frac{1}{2}×\text{AC×DF}
अर्थात् चतुर्भुज ABCD का क्षेत्रफल=त्रिभुज ABC का क्षेत्रफल +त्रिभुज ACD का क्षेत्रफल
=\frac{1}{2}×\text{AC×BE}+\frac{1}{2}×\text{AC×DF}
=\frac{1}{2}×\text{AC}×\text{BE+DF}
अर्थात् चतुर्भुज ABCD का क्षेत्रफल=\frac{1}{2}×विकर्ण ×विकर्णों पर डाले गए लम्बों का योग
Also Read This Article:Chapter 11
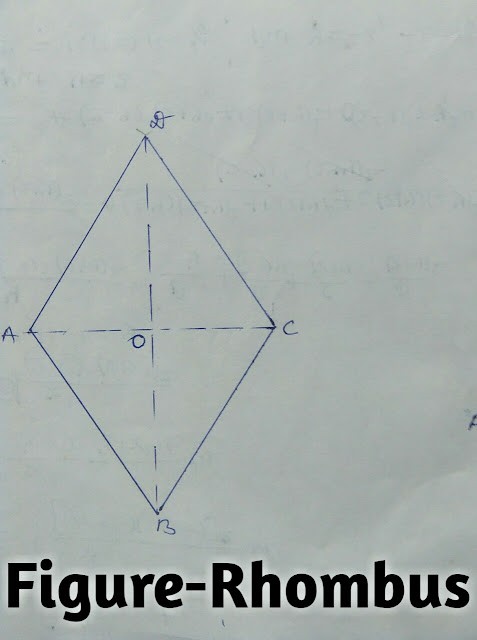
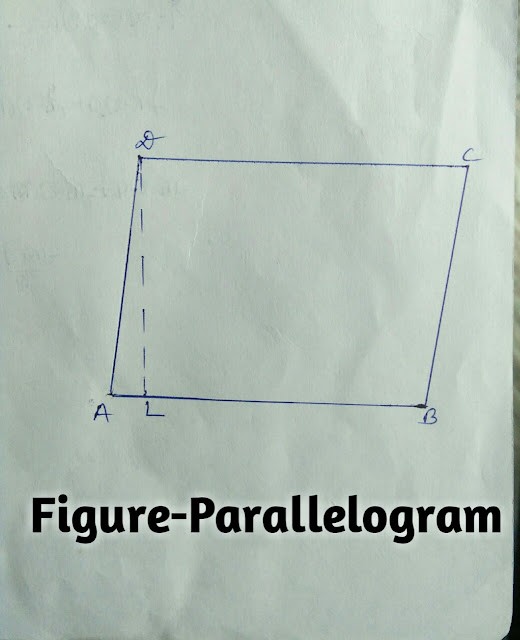
(1)समचतुर्भज (Rhombus) (2.)समान्तर चतुर्भुज (Parallelogram)
चतुर्भुज का क्षेत्रफल (Area of Quadrilateral)
- एक समतल बन्द आकृति द्वारा किसी तल पर घेरा हुआ भाग उस आकृति का तलीय क्षेत्र कहलाता है और इस तलीय क्षेत्र का परिमाण या माप उस आकृति का क्षेत्रफल (area) कहलाता है। इस परिमाप या माप को सदैव किसी मात्रक की सहायता से व्यक्त किया जाता है जैसे 10 वर्ग सेमी, 25 वर्गमीटर इत्यादि।
- For more information please go to this link”https://www.satyamcoachingcentre.in/formula-area-of-quadrilaterals “
चतुर्भुज का क्षेत्रफल (area of quadrilateral):
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
About this website
- अधिक जानकारी के लिए कृपया हमारी वेबसाइट “https://www.satyamcoachingcentre.in/” पर जाएं और इस वेबसाइट का पालन करें जो आप कर सकते हैं। अब किसी को भी गणित की शिक्षा के बारे में समस्या मिल सकती है, विशेष रूप से गणित 8 वीं, 9 वीं, 10 वीं, 11 वीं, 12 वीं, बीएससी, M.sc और उच्च डिग्री कक्षाएं, बैंक, क्लर्क, कांस्टेबल, एसएससी, रेलवे, आरएएस, आईसीएस, वनपाल, आईएफएस, आयकर, एयरफोर्स और अन्य कई प्रतियोगिताओं जैसे प्रतियोगिता गणित। इस वेबसाइट पर आप मानसिक क्षमता की समस्या का समाधान प्राप्त कर सकते हैं, उपरोक्त प्रतियोगिता के तर्क। कई छात्रों को उपरोक्त विषय में सामना करना पड़ता है। इस प्लेटफ़ॉर्म पर आप आसान विधि द्वारा उनके समाधान प्राप्त कर सकते हैं।मेरे पास लगभग 20 साल का अनुभव है और मुझे लगता है कि कई छात्रों को उनकी समस्या नहीं मिल सकती है। कोचिंग सेंटर में वे अपने शुल्क को वहन नहीं करते हैं इसलिए उनकी प्रतिभा का पर्दाफाश नहीं होता है। मुझे उम्मीद है कि आप मेरा समर्थन करेंगे और अपनी समस्या का समाधान ढूंढेंगे।
- (For more information please visit our website “https://www.satyamcoachingcentre.in/ ” and follow this website you can .Now anyone can find there problem about mathematics education specially mathematics upto 8th, 9th, 10th, 11th, 12th, B. Sc., M.sc. and higher degree classes,Competition mathematics like Bank, Clerk, Constable, SSC, Railway, R.A.S., I.C.S., Forester, I.F.S., Income Tax, Airforce and other many competition .At this website you can get solution of problem of mental ability ,Reasoning of above competition. Many students faces in above subject. On this platform you can get their solutions by easy method. I have about 20 years experience and find that many students can’t find their problem. In the coaching centre they do not afford their charges so their talent is not expose. I will hope that you will be support me and find your problem’s solution.)
- उपर्युक्त आर्टिकल में चतुर्भुज का क्षेत्रफल (Area of Quadrilateral) के बारे में बताया गया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |