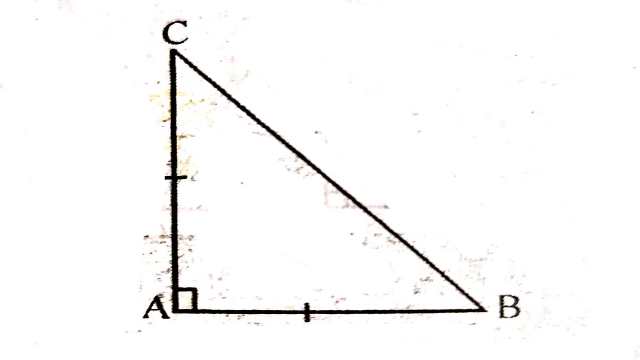Some Properties of Triangle Class 9
1.त्रिभुज के कुछ गुण कक्षा 9 (Some Properties of Triangle Class 9),त्रिभुजों के विशेष गुणधर्म कक्षा 9 (Special Properties of Triangles Class 9):
त्रिभुज के कुछ गुण कक्षा 9 (Some Properties of Triangle Class 9) में समद्विबाहु त्रिभुज के गुणधर्मों का अध्ययन करेंगे।एक त्रिभुज जिसकी दो भुजाएँ बराबर हों समद्विबाहु त्रिभुज (Isosceles Triangle) कहलाता है।
प्रमेय (Theorem):7.2.एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
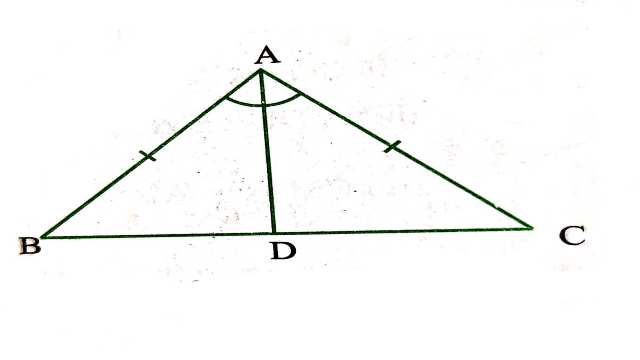
दिया है (Given):\triangle ABC में AB=AC
सिद्ध करना है (To Prove): \angle B=\angle C
रचना (Construction):\angle A का समद्विभाजक AD खींचा जो BC को D पर मिले।
उपपत्ति (Proof): \triangle ABD \text { तथा } \triangle ACD में
AB=AC (दिया है)
\angle BAD=\angle CAD (रचना से)
AD=AD (उभयनिष्ठ है)
\triangle BAD \cong \triangle CAD (SAS नियम द्वारा)
\therefore \angle ABD=\angle ACD
अर्थात् \angle B=\angle C
प्रमेय (Theorem):7.3.किसी त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती है।
दिया है (Given):एक \triangle ABC जिसमें \angle B=\angle C
सिद्ध करना है (To Prove):AB=AC
रचना (Construction):\angle A का समद्विभाजक AD खींचा।
उपपत्ति (Proof): \triangle ABD \text { और } \triangle ACD में
AD=AD (उभयनिष्ठ है)
\angle B=\angle C (दिया है)
\angle BAD=\angle CAD (रचना से)
\triangle ABD \cong \triangle ACD (AAS नियम से)
AB=AC (CPCT)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Triangle Class 9
2.त्रिभुज के कुछ गुण कक्षा 9 पर आधारित उदाहरण (Examples Based on Some Properties of Triangle Class 9):
Example:1.एक समद्विबाहु त्रिभुज ABC में जिसमें AB=AC है, \angle B और \angle C के समद्विभाजक परस्पर बिन्दु O पर प्रतिच्छेद करते हैं।A और O को जोड़िए।दर्शाइए कि
(i) OB=OC
(ii) AO कोण A को समद्विभाजित करता है
Solution:दिया है (Given):एक समद्विबाहु \triangle ABC जिसमें AB=AC है।\angle B और \angle C के समद्विभाजक O पर मिलते हैं।A और O को मिलाया गया है।
सिद्ध करना है (To Prove):(i) OB=OC
(ii) AO कोण A को समद्विभाजित करता है।
उपपत्ति (Proof):(i)\angle ABC=\angle ACB (बराबर भुजाओं के अभिमुख कोण)
\frac{1}{2} \angle ABC=\frac{1}{2} \angle ACB \\ \angle OBC=\angle OCB
OB=OC (बराबर कोणों की अभिमुख भुजाएँ)
(ii) \triangle AOB \text { और } \triangle AOC में
OB=OC (सिद्ध किया है)
AB=AC (दिया है)
AO=AO (उभयनिष्ठ है)
\triangle AOB \cong \triangle AOC (SSS नियम से)
\angle OAB=\angle OAC (CPCT)
अतः AO, \angle A का समद्विभाजक है।
Example:2. \triangle ABC में AD भुजा BC का लम्ब समद्विभाजक है (देखिए आकृति)।दर्शाइए कि \triangle ABC एक समद्विबाहु त्रिभुज है जिसमें AB=AC है।
Solution:दिया है (Given): \triangle ABC में AD,BC का लम्ब समद्विभाजक है।अर्थात् BD=DC, BC \perp AD
सिद्ध करना है (To Prove):\triangle ABC समद्विबाहु त्रिभुज है जिसमें AB=AC
उपपत्ति (Proof): \triangle ADB और \triangle ADC में
\angle ADB=\angle ADC=90^{\circ}
AD=AD (उभयनिष्ठ है)
BD=DC (दिया है)
\triangle ADB \cong \triangle ADC (SAS नियम से)
AB=AC (CPCT)
\therefore \triangle ABC एक समद्विबाहु त्रिभुज है जिसमें AB=AC है।
Example:3.ABC एक समद्विबाहु त्रिभुज है जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलम्ब BE और CF खींचे गए हैं (देखिए आकृति)।दर्शाइए कि ये शीर्षलम्ब बराबर हैं।
Solution:दिया है (Given):\triangle ABC में BE \perp AC \text { व } CF \perp AB तथा AB=AC
सिद्ध करना है (To Prove):BE=CF
उपपत्ति (Proof): \triangle BEC तथा \triangle CFB में
BC=BC (उभयनिष्ठ है)
\angle ACB=\angle ABC (बराबर भुजाओं के अभिमुख कोण)
\angle BEC=\angle CFB=90^{\prime} (दिया है)
\triangle BEC \cong \triangle CFB (AAS नियम से)
BE=CF (CPCT)
Example:4.ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर हैं (देखिए आकृति)।दर्शाइए कि
(i) \triangle ABE \cong \triangle ACF
(ii)AB=AC अर्थात् \triangle ABC एक समद्विबाहु त्रिभुज है।
Solution:दिया है (Given): \triangle ABC में BE \perp AC, CF \perp AB तथा BE=CF
सिद्ध करना है (To Prove):(ii)AB=AC अर्थात् एक समद्विबाहु त्रिभुज है।
उपपत्ति (Proof):(i) \triangle ABE \cong \triangle ACF
(ii) AB=AC अर्थात् एक समद्विबाहु त्रिभुज है।
उपपत्ति (Proof):(i) \triangle ABE \text { और } \triangle ACF में
BE=CF (दिया है)
\angle BAE=\angle CAF (उभयनिष्ठ है)
\angle AEB=\angle AFC=90^{\circ}
\triangle ABE \cong \triangle ACF(AAS नियम से)
(ii) \triangle ABE \cong \triangle ACF(सिद्ध किया है)
\therefore AB=AC (CPCT)
\triangle ABC एक समद्विबाहु त्रिभुज है।
Example:5. \triangle ABC और \triangle DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति)।दर्शाइए कि \angle ABD=\angle ACD है।
Solution:दिया है (Given): \triangle ABC में AB=AC तथा \triangle DBC में BD=CD
सिद्ध करना है (To Prove): \angle ABD=\angle ACD
उपपत्ति (Proof): \triangle ABC समद्विबाहु त्रिभुज है अतः \angle ABC=\angle ACB \cdots(1) \\ \triangle DBC समद्विबाहु त्रिभुज है अतः
\angle DBC=\angle DCB \cdots(2)
(1) व (2) के संगत पक्षों को जोड़ने परः
\angle ABC+\angle DBC=\angle ACB+\angle DCB \\ \Rightarrow \angle ABD=\angle ACD
Example:6.ABC एक समद्विबाहु त्रिभुज है जिसमें AB=AC है।भुजा BA बिन्दु D तक इस प्रकार बढ़ाई गई है कि AD=AB है (देखिए आकृति)।दर्शाइए कि \angle BCD एक समकोण है।
Solution:दिया है (Given):\triangle ABC एक समद्विबाहु त्रिभुज है जिसमें AB=AC
भुजा BA बिन्दु D तक इस प्रकार बढ़ाई गई है कि AD=AB
सिद्ध करना है (To Prove): \angle BCD=90^{\circ}
उपपत्ति (Proof):\triangle ABC समद्विबाहु त्रिभुज है
\therefore \angle ABC=\angle ACB \ldots(1)
AB=AC और AD=AB (दिया है)
\therefore AD=AC
\triangle ACD में
AC=AD
\therefore ACD=\angle ADC (बराबर भुजाओं के अभिमुख कोण)… (2)
समीकरण (1) व (2) के संगत पक्षों को जोड़ने परः
\angle ABC+\angle ADC=\angle ACB+\angle ACD \\ \Rightarrow \angle ABC+\angle ADC=\angle BCD
दोनों पक्षों में \angle BCD जोड़ने परः
\angle ABC+\angle ADC+\angle BCD=\angle BCD+\angle BCD \\ \Rightarrow 180^{\circ}=2 \angle BCD [के तीनों कोणों का योग]
\Rightarrow \angle BCD=90^{\circ}
Example:7.ABC एक समकोण त्रिभुज है जिसमें \angle A=90^{\circ} और AB=AC है। \angle B और \angle C ज्ञात कीजिए।
Solution:समकोण \triangle ABC में
AB=AC
अतः \angle B=\angle C (बराबर भुजाओं के अभिमुख कोण)… (1)
\angle A+\angle B+\angle C=180^{\circ} \\ \Rightarrow 90^{\circ}+\angle C+\angle C=180^{\circ} [ \angle B=\angle C (1) से]
\Rightarrow 2 \angle C=180-90^{\circ} \\ \Rightarrow 2 \angle C=90^{\circ} \\ \Rightarrow \angle C=45^{\circ}
Example:8.दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
Solution:दिया है (Given):समबाहु त्रिभुज है अर्थात् AB=BC=CA
सिद्ध करना है (To prove): \angle A=\angle B=\angle C=60^{\circ}
उपपत्ति (Proof): \triangle ABC में
AB=AC (दिया है)
\angle B=\angle C (बराबर भुजाओं के अभिमुख कोण)… (1)
पुनः BC=AC (दिया है)
\angle A=\angle C (बराबर भुजाओं के अभिमुख कोण)…. (2)
(1) व (2) सेः
\angle A=\angle B=\angle C \cdots(3)
परन्तु \angle A+\angle B+\angle C=180^{\circ} (त्रिभुज के तीनों कोणों का योग)
3 \angle A=180^{\circ} [(3) से]
\angle A=60^{\circ}
अतः \angle A=\angle B=\angle C=60^{\circ}
उपर्युक्त उदाहरणों के द्वारा त्रिभुज के कुछ गुण कक्षा 9 (Some Properties of Triangle Class 9),त्रिभुजों के विशेष गुणधर्म कक्षा 9 (Special Properties of Triangles Class 9) को समझ सकते हैं।
3.त्रिभुज के कुछ गुण कक्षा 9 पर आधारित सवाल (Questions Based on Some Properties of Triangle Class 9):
(1.)यदि एक समद्विबाहु त्रिभुज ABC की माध्यिका AD हो तथा \angle A=120^{\circ} एवं AB=AC हो तो \angle ADB का मान ज्ञात कीजिए।
(2.)दी गई आकृति में AB=AC,BD=EC तो सिद्ध कीजिए कि \triangle ADE एक समद्विबाहु त्रिभुज है।
उपर्युक्त सवालों को हल करने पर त्रिभुज के कुछ गुण कक्षा 9 (Some Properties of Triangle Class 9),त्रिभुजों के विशेष गुणधर्म कक्षा 9 (Special Properties of Triangles Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Angle Sum Property of Triangle Class 9
4.त्रिभुज के कुछ गुण कक्षा 9 (Frequently Asked Questions Related to Some Properties of Triangle Class 9),त्रिभुजों के विशेष गुणधर्म कक्षा 9 (Special Properties of Triangles Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.त्रिभुज किसे कहते हैं? (What is a Triangle?):
उत्तर:तीन असंरेख बिन्दुओं में से दो-दो को मिलाने से बने तीन रेखाखण्डों से बनी आकृति को त्रिभुज कहते हैं।
प्रश्न:2.भुजाओं के आधार पर त्रिभुजों का वर्गीकरण करो। (Classify Triangles Based on Sides):
उत्तर:(1.)विषमबाहु त्रिभुज (Scalene Triangle):जिस त्रिभुज की तीनों भुजाएँ अलग-अलग माप की हों उसे विषमबाहु त्रिभुज कहते हैं।
(2.)समद्विबाहु त्रिभुज (Isosceles Triangle):यदि किसी त्रिभुज की दो भुजाएँ समान माप की हों तो उसे समद्विबाहु त्रिभुज कहा जाता है।
(3.)समबाहु त्रिभुज (Equilateral Triangle):जिस त्रिभुज में सभी भुजाएँ समान माप की हों उसे समबाहु त्रिभुज कहते हैं।
प्रश्न:3.कोणों के आधार पर त्रिभुजों का वर्गीकरण करो। (Classify Triangles Based on Angles):
उत्तर:(1.)न्यूनकोण त्रिभुज (Acute Angled Triangle):जिस त्रिभुज का प्रत्येक कोण न्यूनकोण हो उसे न्यूनकोण त्रिभुज कहते हैं।
(2.)समकोण त्रिभुज (Right Angled Triangle):जिस त्रिभुज का कोई एक कोण 90° के बराबर हो उसे समकोण त्रिभुज कहते हैं।
(3.)अधिककोण त्रिभुज (Obtuse Angled Triangle):जिस त्रिभुज में कोई एक कोण 90° से अधिक हो, उसे अधिक कोण त्रिभुज कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुज के कुछ गुण कक्षा 9 (Some Properties of Triangle Class 9),त्रिभुजों के विशेष गुणधर्म कक्षा 9 (Special Properties of Triangles Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Some Properties of Triangle Class 9
त्रिभुज के कुछ गुण कक्षा 9
(Some Properties of Triangle Class 9)
Some Properties of Triangle Class 9
त्रिभुज के कुछ गुण कक्षा 9 (Some Properties of Triangle Class 9) में समद्विबाहु त्रिभुज
के गुणधर्मों का अध्ययन करेंगे।एक त्रिभुज जिसकी दो भुजाएँ बराबर हों समद्विबाहु
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.