1.त्रिभुज कक्षा 9 (Triangle Class 9),त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9):

Triangle Class 9

त्रिभुज कक्षा 9 (Triangle Class 9) में तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बन्द आकृति (Closed Figure) एक त्रिभुज (Triangle) कहलाती है।’त्रि’ का अर्थ है ‘तीन’।एक त्रिभुज की तीन भुजाएँ,तीन कोण और तीन शीर्ष (Vertices) होते हैं।
अभिगृहीत (Axioms):7.1.दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अन्तर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अन्तर्गत कोण के बराबर हो।
इस परिणाम को इससे पहले ज्ञात परिणामों की सहायता से सिद्ध नहीं किया जा सकता है और इसीलिए इसे एक अभिगृहीत के रूप में सत्य मान लिया गया है।
प्रमेय (Theorem):7.1.दो त्रिभुज सर्वांगसम होते हैं,यदि एक त्रिभुज के दो कोण और उनकी अन्तर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अन्तर्गत भुजा के बराबर हों।
दिया है (Given):दो $\triangle$ ABC और $\triangle$ DEF में $\angle B=\angle E, \angle C=\angle F$ और BC=BF
सिद्ध करना है (To Prove): $\triangle ABC \cong \triangle DEF$
उपपत्ति (Proof):सर्वांगसमता के लिए यहाँ तीन अवस्थाएँ हो सकती हैंः
(i) AB=DE  (ii)AB>DE  (iii)AB<DE

Triangle Class 9

स्थिति (i) माना AB=DE
$\triangle$ ABC और $\triangle$ DEF में
AB=DE  (रचना से)
$\angle B=\angle E$(दिया है)
BC=EF  (दिया है)

अतः $\triangle ABC \cong \triangle DEF$ (SAS नियम द्वारा)
स्थिति (ii) यदि सम्भव हो तो माना AB > DE

Triangle Class 9

रचना : माना AB पर एक बिन्दु P इस इस प्रकार है कि : PB=DE
$\triangle$ PBC और $\triangle$ DEF में
PB=DE(रचना)
$\angle B=\angle E$(दिया है)
BC=EF(दिया है)
इस प्रकार $\triangle PBC \cong \triangle DEF$ (SAS सर्वांगसमता अभिगृहीत द्वारा)
चूँकि दोनों त्रिभुज सर्वांगसम हैं इसलिए इनके संगत कोण बराबर होने चाहिए।
अतः $\angle PCB=\angle DEF$  (CPCT)
$\angle ACB=\angle DFE$ (दिया है)
अतः $\angle ACB=\angle PCB$
यह तभी सम्भव है जब P बिन्दु A के संपाती हो।
$\therefore$  BA=ED
अतः $\triangle ABC \cong \triangle DEF$ (SAS अभिगृहीत द्वारा)
स्थिति (iii). माना AB<DE

Triangle Class 9

रचना (Construction):DE पर M इस प्रकार लिया कि ME=AB
अब $\triangle$ ABC और $\triangle$ MEF में
AB=ME  (रचना से)
$\angle B=\angle E$(दिया है)
BC=EF  (दिया है)
$\therefore \triangle ABC \cong \triangle MEF$ (SAS अभिगृहीत द्वारा)

$\angle C=\angle MEF$(CPCT)
परन्तु $\angle C=\angle DFE \\ \therefore \angle MEF=\angle DFE$
जो कि तभी संभव है जब M और D संपाती हैं।

$\therefore$ ME=DE
अतः $\triangle ABC \cong \triangle DEF$ (SAS अभिगृहीत द्वारा)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:- Angle Sum Property of Triangle Class 9

2.त्रिभुज कक्षा 9 के साधित उदाहरण (Triangle Class 9 Solved Examples):

Example:1.चतुर्भुज ABCD में, AC=AD है और AB कोण A को समद्विभाजित करता है (देखिए आकृति)।दर्शाइए कि $\triangle ABC \cong \triangle ABD$ है।
BC और BD के बारे में आप क्या कह सकते हैं?

Triangle Class 9

Solution:दिया है (Given):चतुर्भुज ABCD में AC=AD तथा $\angle CAB=\angle DAB$
सिद्ध करना है (To Prove): $\triangle ABC \cong \triangle ABD$
उपपत्ति (Proof): $\triangle$ ABC और $\triangle$ ABD में
AB=AB  (उभयनिष्ठ है)
$\angle BAC=\angle BAD$ (दिया है)
AC=AD  (दिया है)
$\triangle ABC \cong \triangle ABD$ (SAS सर्वांगसमता अभिगृहीत द्वारा)
अतः BC=BD   (CPCT)
Example:2.ABCD एक चतुर्भुज है, जिसमें AD=BC और $\angle DAB=\angle CBA$ है (देखिए आकृति)।सिद्ध कीजिए कि
(i) $\triangle ABD \cong \triangle BAC$
(ii) BD=AC
(iii)$\angle ABD=\angle BAC$
Solution:दिया है (Given):चतुर्भुज ABCD में AD=BC और $\angle DAB=\angle CBA$
सिद्ध करना है (To Prove):(i) $\triangle ABD \cong \triangle BAC$
(ii) BD=AC
(iii)$\angle ABD=\angle BAC$

Triangle Class 9

उपपत्ति (Proof):(i) $\triangle$ ABD और $\triangle$ BAC
AB=BA  (उभयनिष्ठ है)
$\angle DAB=\angle CBA$ (दिया है)
AD=BC  (दिया है)
$\therefore \triangle ABD \cong \triangle BAC$ (SAS सर्वांगसमता द्वारा)

(ii) अतः BD=AC   (CPCT)
(iii)$\angle ABD=\angle BAC$ (CPCT)
Example:3.एक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड हैं (देखिए आकृति)।दर्शाइए कि CD, रेखाखण्ड AB को समद्विभाजित करता है।

Triangle Class 9

Solution:दिया है (Given): $AB \perp AD$ तथा $BC \perp AB$
सिद्ध करना है (To Prove):OB=OA
उपपत्ति (Proof): $\triangle$ OAD और $\triangle$ OBC में
AD=BC  (दिया है)
$\angle OAD=\angle OBC$ (प्रत्येक 90° है)
$\angle AOD=\angle BOC$  (शीर्षाभिमुख कोण)
$\triangle OAD \cong \triangle OBC$ (AAS सर्वांगसमता से)
$\therefore$  OA=OB  (CPCT)
$\therefore$  CD, रेखाखण्ड AB को समद्विभाजित करता है।
Example:4.l और m दो समान्तर रेखाएँ हैं जिन्हें समान्तर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति)।दर्शाइए कि $\triangle ABC \cong \triangle CDA$

Triangle Class 9

Solution:दिया है (Given): AD || BC तथा AB || CD
सिद्ध करना है (To Prove): $\triangle ABC \cong \triangle CDA$
उपपत्ति (Proof):AD || BC तथा AB || CD
(अतः चतुर्भुज ABCD समान्तर चतुर्भुज होता है यदि सम्मुख भुजाओं के दोनों युग्म समान्तर हों)
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएँ) … (1)
CD=AB  (समान्तर चतुर्भुज की सम्मुख भुजाएँ)… (2)
$\angle CDA=\angle ABC$ (समान्तर चतुर्भुज के सम्मुख कोण) … (3)
$\triangle$ CDA और $\triangle$ ABC में
CD=AB  [(2) से]
DA=BC  [(1) से]
$\angle CDA=\angle ABC$ [(3) से]
$\triangle CDA \cong \triangle ABC$ (SAS सर्वांगसमता नियम से)
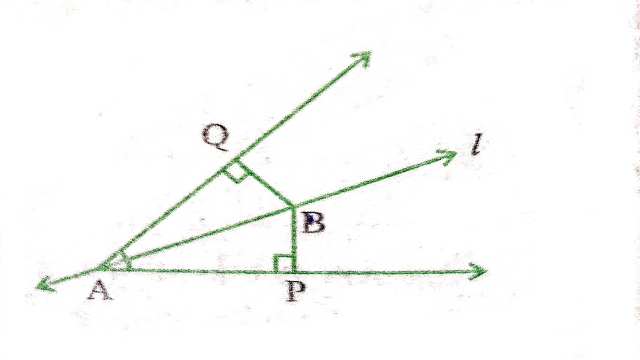
Example:5.रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिन्दु है।BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं (देखिए आकृति)।दर्शाइए
(i) $\triangle APB \cong \triangle AQB$
(ii) BP=BQ है अर्थात् बिन्दु B कोण की भुजाओं से समदूरस्थ है।

Triangle Class 9

Solution:दिया है (Given): $\angle BAQ=\angle BAP$ तथा $BP \perp BQ$
सिद्ध करना है (To Prove): (i)$\triangle APB \cong \triangle AQB$
(ii) BP=BQ अर्थात् बिन्दु B कोण की भुजाओं से समदूरस्थ है
उपपत्ति (Proof):(i) $\triangle$ APB और $\triangle$ AQB में
$\angle BAP=\angle BAQ$ (l, $\angle A$ का अर्धक है)
AB=AB  (उभयनिष्ठ है)
$\angle BPA=\angle BQA$ (प्रत्येक 90° है)
($\because$ BQ और BP कोण A की भुजाओं पर B से डाले गए लम्ब हैं)
$\triangle APB \cong \triangle AQB$ (AAS सर्वांगसमता नियम से)
(ii) $\triangle APB \cong \triangle AQB$ (सिद्ध किया है)
BP=BQ  (CPCT)
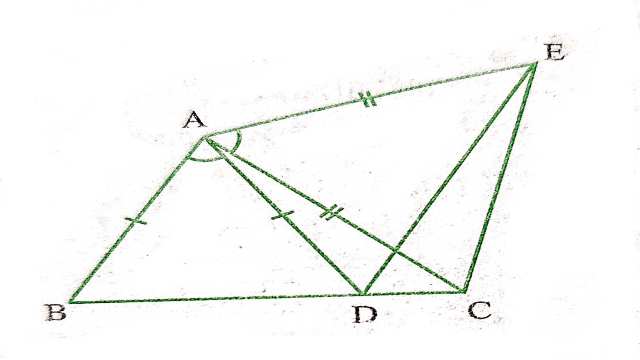
Example:6.आकृति में AC=AE, AB=AD और $\angle BAD=\angle EAC$ है।दर्शाइए कि BC=DE है।
Solution:दिया है (Given):AC=AE, AB=AD और  $\angle BAD=\angle EAC$
सिद्ध करना है (To Prove):BC=DE

Triangle Class 9

उपपत्ति (Proof): $\angle BAD=\angle EAC$ (दिया है)
दोनों पक्षों में $\angle$ DAC जोड़ने परः

$\angle BAD+\angle DAC=\angle EAC+\angle DAC \\ \Rightarrow \angle BAC=\angle DAE \cdots\text {(1)} \\ \triangle ABC$ और $\triangle$ ADE में
AB=AD (दिया है)
AC=AE  (दिया है)
$\angle BAC=\angle DAE$  [(1) से]
$\therefore \triangle ABC \cong \triangle ADE$ (SAS सर्वांगसमता नियम से)
$\therefore$ BC=DE  (CPCT)
Example:7.AB एक रेखाखण्ड है और P इसका मध्य-बिन्दु है। D और E रेखाखण्ड AB के एक ही ओर स्थित दो बिन्दु इस प्रकार हैं कि $\angle BAD=\angle ABE$ और $\angle EPA=\angle DPB$ है। (देखिए आकृति)।दर्शाइए कि
(i) $\triangle DAP \cong \triangle EBP$
(ii)AD=BE

Triangle Class 9

Solution:दिया है (Given):AP=PB, $\angle BAD=\angle ABE$ और $\angle EPA=\angle DPB$
सिद्ध करना है (To Prove): (i) $\triangle DAP \cong \triangle EBP$
(ii) AD=BE
उपपत्ति (Proof):(i)$\angle APE=\angle DPB$ (दिया है)
दोनों पक्षों में $\angle EPD$ जोड़ने परः

$\angle APE+\angle EPD=\angle DPB+\angle EPD \\ \Rightarrow \angle APD=\angle EPB \cdots(1) \\ \triangle DAP$ और $\triangle EBP$ में
$\angle DAP=\angle EBP$ (दिया है)
$\angle APD=\angle EPB$ [(1) से]
AP=BP  (दिया है)
$\therefore \triangle DAP \cong \triangle EBP$ (ASA सर्वांगसमता नियम से)

(ii) अतः AD=BE(CPCT)
Example:8.एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिन्दु है।C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM=CM है।बिन्दु D को बिन्दु B से मिला दिया जाता है (देखिए आकृति)।दर्शाइए कि
(i) $\triangle AMC \cong \triangle BMD$
(ii) $\angle DBC$ एक समकोण है
(iii) $\triangle DBC \cong \triangle ACB$
(iv) $CM=\frac{1}{2} AB$

Triangle Class 9

Solution:दिया है (Given): $\triangle ABC$ में $\angle C$=90°, AM=BM तथा DM=CM
सिद्ध करना है (To Prove): (i) $\triangle AMC \cong \triangle BMD$
(ii) $\angle DBC$ एक समकोण है
(iii) $\triangle DBC \cong \triangle ACB$
(iv) $CM=\frac{1}{2} AB$
उपपत्ति (Proof):(i) $\triangle AMC$ और $\triangle BMD$ में
AM=BM  (दिया है)
CM=DM  (दिया है)
$\angle AMC=\angle BMD$ (शीर्षाभिमुख कोण)
$\therefore \triangle AMC \cong \triangle BMD$ (SAS सर्वांगसमता नियम से)
(ii) $\angle CAM=\angle DBM$ (CPCT)……(1)
तथा $\angle CAM+\angle MBC=90^{\circ}$ [चूँकि $\angle C$=90° ]
$\therefore \angle DBM+\angle MBC=90^{\circ}$ [(1) से]

$\Rightarrow \angle DBC=90^{\circ}$
(iii) $\triangle DBC$ और $\triangle ACB$ में
BC=BC  (उभयनिष्ठ है)
DB=AC ( $\triangle BMD \cong \triangle AMC$,CPCT )
$\angle DBC=\angle ACB=90^{\circ}$ (सिद्ध किया है)
अतः $\triangle DBC \cong \triangle ACB$ (SAS सर्वांगसमता नियम से)
(iv) चूँकि $\triangle DBC \cong \triangle ACB$

DC=AB
इस प्रकार $\frac{1}{2} DC=\frac{1}{2} AB$
CM=AM
[अतः M, AB तथा DC का मध्य बिन्दु है]
अतः $CM=\frac{1}{2} AB$
उपर्युक्त उदाहरणों के द्वारा त्रिभुज कक्षा 9 (Triangle Class 9),त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9) को समझ सकते हैं।

3.त्रिभुज कक्षा 9 पर आधारित सवाल (Questions Based on Triangle Class 9):

(1.)नीचे दी गई आकृति में BA भुजा AC पर एवं DE भुजा EF पर लम्बवत है एवं BA=DE और BF=CD हो तो सिद्ध कीजिए कि AC=EF।

Triangle Class 9

(2.)आकृति ABCD एक चतुर्भुज है जिसमें AB=AD और BC=DC है।सिद्ध कीजिए किः
(i) AC कोण A और C में से प्रत्येक को समद्विभाजित करता है।
(ii) BE=ED
(iii) $\angle ABC= \angle ADC$ क्या हम कह सकते हैं कि AE=EC

Triangle Class 9

उपर्युक्त सवालों को हल करने पर त्रिभुज कक्षा 9 (Triangle Class 9),त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9) को ठीक से समझ सकते हैं।

4.त्रिभुज कक्षा 9 की मुख्य बातें (HIGHLIGHTS of Triangle Class 9):

Triangle Class 9

(1.)दो आकृतियां सर्वांगसम होती हैं यदि उनका एक ही आकार हो और एक ही माप हो।
(2.)दो समान त्रिज्याओं वाले वृत्त सर्वांगसम होते हैं।
(3.)समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।
(4.)यदि  $\triangle ABC$ और $\triangle PQR$ संगतता $A \leftrightarrow P,B \leftrightarrow Q$ और $C \leftrightarrow R$ के अन्तर्गत सर्वांगसम हों तो उन्हें सांकेतिक रूप में $\triangle PQR \cong \triangle ABC$ लिखते हैं।
(5.)यदि एक त्रिभुज की दो भुजाएँ और अन्तर्गत कोण दूसरे त्रिभुज की दो भुजाओं और अन्तर्गत कोण दूसरे त्रिभुज की दो भुजाओं और अन्तर्गत कोण के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।
(6.)यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और अन्तर्गत भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।
(7.)यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।

Also Read This Article:-Parallel Lines and Transversal Lines

5.त्रिभुज कक्षा 9 (Frequently Asked Questions Related to Triangle Class 9),त्रिभुजों की सर्वांगसमता कक्षा 9 (Congruence of Triangles Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः

त्रिभुज कक्षा 9 (Triangle Class 9) में तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बन्द
आकृति (Closed Figure) एक त्रिभुज (Triangle) कहलाती है।’त्रि’ का अर्थ है ‘तीन’।