Angle Sum Property of Triangle Class 9
1.त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of Triangle Class 9),त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of a Triangle):
त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of Triangle Class 9) से तात्पर्य है कि एक त्रिभुज के सभी कोणों का योग 180° होता है।हम इस कथन को समान्तर रेखाओं से सम्बन्धित अभिगृहीतों और प्रमेयों का प्रयोग करके सिद्ध कर सकते हैं।
प्रमेय (Theorem):6.7.किसी त्रिभुज के कोणों का योग 180° होता है।
दिया है (Given): \triangle PQR
सिद्ध करना है (To Prove): \angle 1+\angle 2+\angle 3=180^{\circ}
रचना (Construction):QR के समान्तर एक रेखा P से खींची।
उपपत्ति (Proof): QR \parallel XY \\ \therefore \angle 4=\angle 2 और \angle 5=\angle 3 (एकान्तर कोणों के युग्म)
XPY एक रेखा है अतः
\angle 4+\angle 1+\angle 5=180^{\circ} \ldots(2)
(1) व (2) सेः
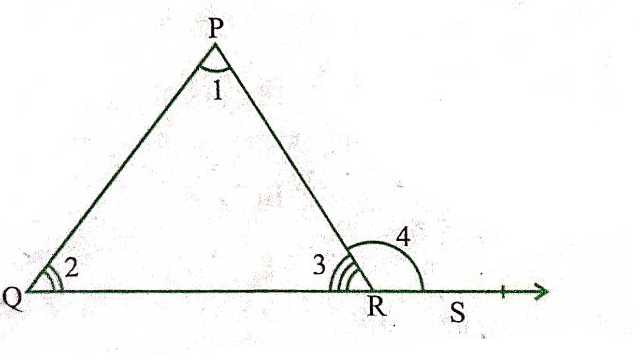
प्रमेय (Theorem):6.8.यदि एक त्रिभुज की एक भुजा बढ़ाई जाए तो इस प्रकार बना बहिष्कोण दोनों अन्तःअभिमुख (विपरीत) कोणों (interior Opposite Angles) के योग के बराबर होता है।
दिया है (Given): \triangle PQR जिसमें भुजा QR को S तक बढ़ाया गया है और इस प्रकार का बाह्य \angle PRS बनता है।
सिद्ध करना है (To Prove): \angle 4=\angle 1+\angle 2
उपपत्ति (Proof): \angle 1+\angle 2+\angle 3=180^{\circ} \ldots(1) (एक त्रिभुज के तीनों अन्तःकोणों का योग)
\angle 3+\angle 4=180^{\circ} (रैखिक युग्म अभीगृहीत से)
(1) व (2) सेः
\angle 3+\angle 4=\angle 1+\angle 2+\angle 3 \\ \Rightarrow \angle 4=\angle 1+\angle 2
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Lines and Angles Class 9
2.त्रिभुज का कोण योग गुण कक्षा 9 के साधित उदाहरण (Angle Sum Property of Triangle Class 9 Solved Examples):
Example:1.आकृति में \triangle PQR की भुजाओं QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है।यदि [katex]\angle SPR=135^{\circ} और \angle PQT=110^{\circ} है तो ज्ञात कीजिए।
Solution: \angle RPS+\angle QPR=180^{\circ} \ldots(1) (रैखिक युग्म अभिगृहीत से)
परन्तु \angle RPS=135^{\circ} \\ \therefore 135^{\circ}+\angle Q P R=180^{\circ} \\ \Rightarrow \angle Q P R=180^{\circ}-135^{\circ} \\ \Rightarrow \angle Q P R=45^{\circ} \\ \angle TQP=\angle QPR+\angle PRQ
(त्रिभुज का बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है)
\Rightarrow \angle T Q P=110^{\circ}, \angle Q P R=45^{\circ} \\ \therefore 110^{\circ}= 45^{\circ}+ \angle P R Q \\ \Rightarrow \angle P R Q=110^{\circ}-45^{\circ} \\ \Rightarrow \angle PRQ=65^{\circ}
Example:2.आकृति में \angle X=62^{\circ} और \angle XYZ=54^{\circ} है।यदि YO और ZO क्रमशः \triangle XYZ के \angle XYZ और \angle XZY के समद्विभाजक हैं तो \angle OZY और \angle YOZ ज्ञात कीजिए।
Solution:
\triangle XYZ में
\angle X+\angle XYZ+\angle XZY=180^{\circ} (त्रिभुज के अन्तःकोणों का योग)
62^{\circ}+54^{\circ}+\angle X Z Y=180^{\circ} \\ \Rightarrow 116^{\circ}+\angle XZY=180^{\circ} \\ \Rightarrow \angle XZY=180^{\circ}-116^{\circ} \\ \Rightarrow \angle XZY=64^{\circ} \\ \angle X Z Y का अर्धक OZ है अतः
\angle O Z Y=\frac{1}{2} \angle XZY \\ =\frac{1}{2} \times 64^{\circ} \\ \Rightarrow \angle O Z Y=32^{\circ} \\ \angle XYZ का अर्धक YO है
\therefore \angle OYZ=\frac{1}{2} \angle XYZ \\ =\frac{1}{2} \times 54^{\circ} \\ \Rightarrow \angle OYZ=27^{\circ}
अतः \triangle OYZ में
\angle OYZ+\angle YOZ+\angle OZY=180^{\circ} \\ \Rightarrow 27^{\circ}+\angle YOZ+32^{\circ} =180^{\circ} \\ \Rightarrow 59^{\circ}+\angle Y O Z=180^{\circ} \\ \Rightarrow \angle YOZ= 180^{\circ}-59^{\circ} \\ \Rightarrow \angle YOZ=121^{\circ}
अतः \angle OZY=32^{\circ}, \angle Y O Z=121^{\circ}
Example:3.आकृति में यदि A B \| D E, \angle BAC=35^{\circ} और \angle CDE=53^{\circ} है तो \angle DCE ज्ञात कीजिए।
Solution:
A B \| D E \\ \angle DEC=\angle BAC (एकान्तर कोण)
\Rightarrow \angle DEC=35^{\circ} \ldots(1) \\ \triangle DCE में
\angle CDE+\angle DCE+\angle DEC=180^{\circ} (त्रिभुज के अन्तःकोणों का योग)
\Rightarrow 53^{\circ}+\angle D C E+35^{\circ}=180^{\circ} \\ \Rightarrow 88^{\circ}+\angle D C E=180^{\circ} \\ \Rightarrow \angle D C E=180^{\circ}-88^{\circ} \\ \Rightarrow \angle DCE=92^{\circ}
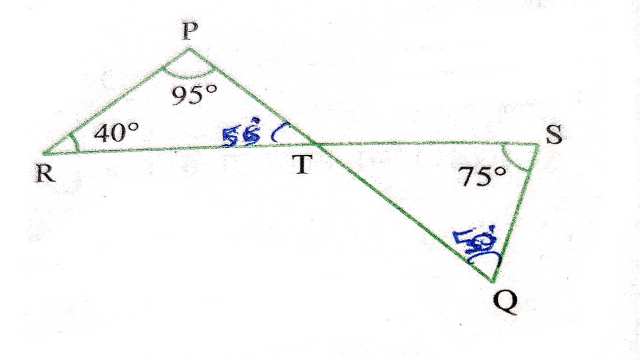
Example:4.आकृति में यदि रेखाएँ PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती हैं कि \angle PRT=40^{\circ} ,\angle R P T=95^{\circ} और \angle TSQ=75^{\circ} है तो \angle SQT ज्ञात कीजिए।
Solution:
\triangle PRT में
\angle PRT+\angle RPT+\angle PTR=180^{\circ} (त्रिभुज के अन्तःकोणों का योग)
40^{\circ}+95^{\circ}+\angle P T R=180^{\circ} \\ \Rightarrow 135^{\circ}+\angle P T R =180^{\circ} \\ \Rightarrow \angle P T R=180^{\circ}-135^{\circ} \\ \angle PTR=45^{\circ} \\ \angle STQ=\angle PTR (शीर्षाभिमुख कोण)
\angle STQ=45^{\circ} \\ \triangle TSQ में
\angle S T Q+\angle T S Q+\angle S Q T=180^{\circ}
(त्रिभुज के अन्तःकोणों का योग)
45^{\circ}+75^{\circ}+\angle S Q T=180^{\circ} \\ \Rightarrow 120^{\circ}+\angle SQT=180^{\circ} \\ \Rightarrow \angle S Q T=180^{\circ}-120^{\circ} \\ \Rightarrow \angle S Q T=60^{\circ}
Example:5.आकृति में,यदि P Q \perp P S ,P Q \| SR, \angle SQR=28^{\circ} और \angle QRT=65^{\circ} है तो x और y के मान ज्ञात कीजिए।
Solution:
P Q \| SR तथा P Q \perp P S \\ \angle Q R T=\angle Q S R+\angle S Q R
(त्रिभुज का बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है)
\Rightarrow 65^{\circ}=\angle Q S R+28^{\circ} \\ \Rightarrow \angle Q S R=65^{\circ}-28^{\circ} \\ \Rightarrow \angle Q S R=37^{\circ} \\ P Q \| S R
अतः \angle P Q S=\angle Q S R (एकान्तर कोण)
x=37°
\triangle PQS में
\angle S P Q+\angle P Q S+\angle P S Q=180^{\circ}
(त्रिभुज के अन्तःकोणों का योग)
90^{\circ}+y+39^{\circ}=180^{\circ} \\ \Rightarrow 127^{\circ}+y=180^{\circ} \\ \Rightarrow y=180^{\circ}-127^{\circ} \\ \Rightarrow y=53^{\circ}, x=37^{\circ}
Example:6.आकृति में \triangle PQR की भुजा QR को बिन्दु S तक बढ़ाया गया है।यदि \angle PQR और \angle PRS के समद्विभाजक बिन्दु T पर मिलते हैं तो सिद्ध कीजिए कि \angle QTR=\frac{1}{2} \angle QPR है।
Solution:
RT, \angle P R S का समद्विभाजक है।
अतः \angle P R S=\angle T R S=\angle P R T \ldots(1)
QT, \angle PQR का समद्विभाजक है अतः
\frac{1}{2} \angle P Q R=\angle T Q R \ldots(2) \\ \triangle TQR में
\angle T R S=\angle T Q R+\angle Q T R \ldots(3)
(बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है)
(1) व (3) सेः
\frac{1}{2} \angle P R S=\angle T Q R+\angle QTR \ldots(4) \\ \triangle P Q R में
\angle P R S=\angle P Q R+\angle Q P R \ldots(5)
(बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है)
(4) व (5) सेः
\frac{1}{2}(\angle P Q R+\angle Q P R)=\angle T Q R+\angle Q T R \\ \Rightarrow \frac{1}{2} \angle P Q R+\frac{1}{2} \angle Q P R=\angle T Q R+\angle Q T R \\ \Rightarrow \angle T Q R+\frac{1}{2} \angle Q P R=\angle T Q R+\angle Q T R[(2)से ]
\Rightarrow \angle QTR=\frac{1}{2} \angle Q P R
उपर्युक्त उदाहरणों के द्वारा त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of Triangle Class 9),त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of a Triangle) को समझ सकते हैं।
3.त्रिभुज का कोण योग गुण कक्षा 9 पर आधारित सवाल (Questions Based on Angle Sum Property of Triangle Class 9):
(1.)आकृति में चतुर्भुज ABCD में AB \| CD है। \angle A=80^{\circ} और \angle B=84^{\circ} है। \angle C और \angle D के कोण-समद्विभाजक क्रमशः P पर मिलते हैं।\angle CPD ज्ञात करो।
(2.)आकृति में \angle ABC और \angle BCA के कोण समद्विभाजक बिन्दु O पर परस्पर प्रतिच्छेद करते हैं।सिद्ध कीजिए कि
\angle BOC=90^{\circ}+\frac{1}{2} \angle Aउत्तर (Answer):(1.) 82°
उपर्युक्त सवालों को हल करने पर त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of Triangle Class 9),त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of a Triangle) को ठीक से समझ सकते हैं।
Also Read This Article:-Parallel Lines and Transversal Lines
4.त्रिभुज का कोण योग गुण कक्षा 9 (Frequently Asked Questions Related to Angle Sum Property of Triangle Class 9),त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of a Triangle) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.रेखाएँ और कोण की मुख्य बातें लिखिए। (Write Down HIGHLIGHTS of Lines and Angles Class 9):
उत्तरः(1.)यदि एक किरण एक रेखा पर खड़ी हो तो इस प्रकार बने दोनों आसन्न कोणों का योग 180° होता है और विलोमतः यदि दो आसन्न कोणों का योग 180° है तो उनकी अउभयनिष्ठ भुजाएँ एक रेखा बनाती हैं।इन गुणों को मिलाकर रैखिक युग्म अभिगृहीत कहते हैं।
(2.)यदि दो रेखाएँ परस्पर प्रतिच्छेद करें तो शीर्षाभिमुख कोण बराबर होते हैं।
(3.)यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करे,तो
(i) संगत कोणों का प्रत्येक युग्म बराबर होता है।
(ii) एकान्तर अन्तःकोणों का प्रत्येक युग्म बराबर होता है।
(iii) तिर्यक रेखा के एक ही ओर के अन्तः कोणों का प्रत्येक युग्म संपूरक होता है।
(4.)यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि या तो
(i) संगत कोणों का कोई एक युग्म बराबर हो या
(ii) एकान्तर अन्तःकोणों का कोई एक युग्म बराबर हो या
(iii) तिर्यक रेखा के एक ही ओर के अन्तःकोणों का कोई एक युग्म संपूरक हो तो ये दोनों रेखाएँ परस्पर समान्तर होती है।
(5.)वे रेखाएँ जो एक ही रेखा के समान्तर होती हैं परस्पर समान्तर होती हैं।
(6.)एक त्रिभुज के तीनों कोणों का योग 180° होता है।
(7.)यदि किसी त्रिभुज की एक भुजा को बढ़ाया जाए तो इस प्रकार बना बहिष्कोण अपने दोनों अन्तः अभिमुख कोणों के योग के बराबर होता है।
प्रश्न:2.प्रतिवर्ती कोण किसे कहते हैं? (What is the Reflex Angle?):
उत्तरःप्रतिवर्ती कोण (वृहत कोण) वह कोण है जो दो समकोण से बड़ा तथा चार समकोण से छोटा हो।
प्रश्न:3.सम्पूरक कोण किसे कहते हैं? (What is Supplementary Angles?):
उत्तरःयदि दो कोणों का योग दो समकोण के तुल्य हो तो वे एक-दूसरे के सम्पूरक कोण कहलाते हैं।
प्रश्न:4.एक चतुर्भुज के तीन कोण दिए हों तो चौथा कोण कैसे ज्ञात करते हैं? (If Three Angles of a Quadrilateral are Give then How to Find the Fourth Angle?):
उत्तरःदिए हुए चतुर्भुज के तीनों कोणों को जोड़कर 360° में से घटाने पर शेषफल चौथा कोण का मान आएगा।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of Triangle Class 9),त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of a Triangle) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Angle Sum Property of Triangle Class 9
त्रिभुज का कोण योग गुण कक्षा 9
(Angle Sum Property of Triangle Class 9)
Angle Sum Property of Triangle Class 9
त्रिभुज का कोण योग गुण कक्षा 9 (Angle Sum Property of Triangle Class 9) से
तात्पर्य है कि एक त्रिभुज के सभी कोणों का योग 180° होता है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.