Arithmetic Progression in Class 10
1.कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10),समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progression Class 10):
कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10) के इस आर्टिकल में कुछ कठिन सवालों का अध्ययन करेंगे।ये ऐच्छिक प्रश्नावली के सवाल हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Sum of First n Terms of an AP in Maths
2.कक्षा 10 में समान्तर श्रेढ़ी पर आधारित उदाहरण (Examples Based on Arithmetic Progression in Class 10):
Example:1.A.P.:121,117,113,….का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
Solution:A.P.:121,117,113,….
a=a_1=121, d=117-121=-4\\ a_n=a+(n-1) d\\ \Rightarrow a_n=121+(n-1) \times-4\\ =121-4 n+4\\ =125-4 n
प्रश्नानुसार a_n<0\\ \Rightarrow 125-4 n<0\\ \Rightarrow 4 n>125\\ \Rightarrow n>\frac{125}{4}\\ \Rightarrow n \geq 31 \frac{1}{4}
n एक धनात्मक पूर्णांक है अतः n=32
Example:2.किसी A.P. के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है।इस A.P. के प्रथम 16 पदों का योग ज्ञात कीजिए।
Solution: a_n=a+(n-1) d \\ a_3=a+2 d \\ a_7=a+6 d \\ a+2 d+a+6 d=6 \\ \Rightarrow 2 a+8 d=6 \\ \Rightarrow a+4 d=\frac{6}{2} \\ \Rightarrow a+4 d=3 \cdots(1) \\ (a+2 d)(a+6 d)=8 \\ \Rightarrow a^2+6 a d+2 a d+12 d^2=8 \\ \Rightarrow a^2+8 a d+12 d^2=8 \\ \Rightarrow(3-4 d)^2+8(3-4 d) d+12 d^2=8 [(1) से]
\Rightarrow 9-24 d+16 d^2+24 d-32 d^2+12 d^2=8\\ \Rightarrow-4 d^2+9=8\\ \Rightarrow 4 d^2=1\\ \Rightarrow d^2=\frac{1}{4} \\ \Rightarrow d=\pm \frac{1}{2}
जब d=\frac{1}{2} तो a+4 \times -\frac{1}{2}=3 [(1) से]
a=3-2 \Rightarrow a=1
जब d=-\frac{1}{2} तो a+4 \times -\frac{1}{2}=3 \Rightarrow a=3+2=5
जब a=1, d=\frac{1}{2}, n=16 \\ S_n =\frac{n}{2}[2 a+(n-1) d] \\ =\frac{16}{2}\left [ 2 \times 1+(16-1) \times \frac{1}{2} \right ] \\ =\frac{16}{2}\left[2+\frac{15}{2}\right] \\ =8 \times \frac{19}{2} \\ \Rightarrow S_{16} =76
जब a=5, d=-\frac{1}{2}, n=16 \\ S_{16} =\frac{16}{2}\left [ 2 \times 5+(16-1) \times-\frac{1}{2} \right ] \\ =8\left[10-\frac{15}{2}\right] \\ =8 \times \frac{5}{2} \\ S_{16} =20
Example:3.एक सीढ़ी के क्रमागत डंडे परस्पर 25cm की दूरी पर हैं (देखिए आकृति) डंडों की आकृति एक समान रूप से घटती जाती है तथा सबसे निचले डंडे की लम्बाई 45cm है और सबसे ऊपर वाले डंडे की लम्बाई 25 सेमी है।यदि ऊपरी और निचले डंडे के बीच दूरी 2.5 मीटर है तो डंडों को बनाने के लिए लकड़ी की कितनी लम्बाई की आवश्यकता होगी?
Solution:प्रथम व अन्तिम डंडे के बीच दूरी=2.5 मीटर =250 सेमी
दो क्रमागत डंडों के बीच दूरी=25 सेमी
सीढ़ी में डंडों की संख्या=\frac{\text{प्रथम व अन्तिम डण्डे के बीच दूरी}}{\text{दो क्रमागत डंडों के बीच दूरी}}+1
=\frac{250}{25}+1=10+1=11
a=25 सेमी, l=45सेमी, n=11
S_n =\frac{n}{2}[a+l) \\ \Rightarrow S_{11} =\frac{11}{2}[25+45] \\ =\frac{11}{2} \times 70 \\ \Rightarrow S_{11} =385 सेमी
Example:4.एक पंक्ति के मकानों को क्रमागत रूप से संख्या 1 से 49 तक अंकित किया गया है।दर्शाइए कि x से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है।x का मान ज्ञात कीजिए।
Solution:मकानों पर क्रमागत रूप से अंकित संख्याएँ 1,2,3,4,5,…,49 हैं।
1 से x-1 तक की संख्याओं का योग=x+1 से 49 तक की संख्याओं का योग
S_n =\frac{n}{2}\left[2 a+(n-1)\right]
1 से x-1 तक की संख्याओं का योग
S_{x-1}=\frac{x-1}{2}[2 \times 1+(x-1-1) \times 1] \\ =\frac{x-1}{2}[2+x-2] \\ \Rightarrow S_{x-1} =\frac{x(x-1)}{2}
x+1 से 49 तक की संख्याओं का योग
n=49-x, a=x+1\\ S_{49-x}=\frac{49-x}{2}[2(x+1)+(49-x-1) \times 1]\\ =\frac{49-x}{2}[2 x+2+48-x]\\ =\frac{(49-x)}{2}(50+x)
प्रश्नानुसारः \frac{x(x-1)}{2}=\frac{(49-x)(50+x)}{2}\\ \Rightarrow x^2-x=2450+49 x-50 x-x^2\\ \Rightarrow 2 x^2-x+x=2450\\ \Rightarrow 2 x^2=2450\\ \Rightarrow x^2=1225\\ \Rightarrow x=35
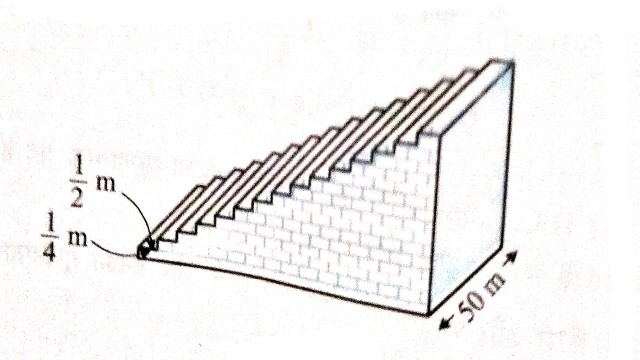
Example:5.एक फुटबाल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं।इन सीढ़ियों में से प्रत्येक की लम्बाई 50 मीटर है और वह ठोस कंक्रीट (concrete) की बनी है।प्रत्येक सीढ़ी में \frac{1}{4} मीटर की चढ़ाई है और \frac{1}{2} मीटर का फैलाव (चौड़ाई) है।(देखिए आकृति) इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
Solution:प्रत्येक सीढ़ी की लम्बाई=50 मीटर
प्रत्येक सीढ़ी की चौड़ाई=\frac{1}{2} मीटर
सीढ़ियों की संख्या n=15
प्रत्येक सीढ़ी की ऊँचाई समान्तर श्रेढ़ी में है अर्थात्
\frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \frac{4}{4}, \frac{5}{4}, \frac{6}{4}, \ldots, \frac{15}{4}
पहली सीढ़ी में लगी कंक्रीट का आयतन=50 \times \frac{1}{2} \times \frac{1}{4}=\frac{50}{8}घन मीटर
दूसरी सीढ़ी में लगी कंक्रीट का आयतन=50 \times \frac{1}{2} \times \frac{2}{4}=\frac{100}{8} घन मीटर
तीसरी सीढ़ी में लगी कंक्रीट का आयतन=50 \times \frac{1}{2} \times \frac{3}{4}=\frac{150}{8} घन मीटर
अतः कंक्रीट का आयतन
=\frac{50}{8}+\frac{160}{8}+\frac{150}{8}+\cdots+15 पदों तक
a=\frac{50}{8}, d=\frac{100}{8}-\frac{50}{8}=\frac{50}{8}, n=15\\ S_n=\frac{n}{2}[2 a+(n-1) d]\\ S_{15}= \frac{15}{2}\left[2 \times \frac{30}{8}+(15-1) \times \frac{50}{8}\right]\\ =\frac{15}{2}\left[\frac{55}{4}+14 \times \frac{50}{8}\right]\\ =\frac{15}{2}\left[\frac{50}{4}+\frac{350}{4}\right]\\ =\frac{15}{2}\left[\frac{400}{4}\right]\\ =\frac{15}{2} \times 100\\ =15 \times 50\\ S_{15}=750 घन मीटर
अतः चबूतरे में लगी कंक्रीट का आयतन=750 घन मीटर
उपर्युक्त उदाहरणों के द्वारा कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10),समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progression Class 10) को समझ सकते हैं।
3.कक्षा 10 में समान्तर श्रेढ़ी पर आधारित सवाल (Questions Based on Arithmetic Progression in Class 10):
(1.)एक समान्तर श्रेणी का 10वाँ पद 52 तथा 16वाँ पद 82 है।इसका 32वाँ पद तथा व्यापक पद ज्ञात कीजिए।
(2.)एक समान्तर श्रेणी का mवाँ पद \frac{1}{n} तथा nवाँ पद \frac{1}{m} हो तो दर्शाइए कि mn पदों का योगफल \frac{1}{2}\left(mn+1 \right) होगा।
उत्तर (Answer):(1.) a_{32}=162 तथा a_n=5 n+2
उपर्युक्त सवालों को हल करने पर कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10),समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progression Class 10) को ठीक से समझ सकते हैं।
Also Read This Article:-Sum of First n Terms of an AP Class 10
4.कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10),समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progression Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.क्या समान्तर श्रेढ़ी का प्रयोग दैनिक जीवन में किया जा सकता है? (Can Arithmetic Progression be Used in Daily Life?):
उत्तर:दैनिक जीवन की कई समस्याओं को हल करने में समान्तर श्रेढ़ी का प्रयोग कर सकते हैं।जैसे शकीला अपनी पुत्री की गुल्लक में उसके 1 वर्ष की हो जाने पर 100 रुपये डालती है, उसके दूसरे जन्म दिवस पर 150 रुपये,तीसरे जन्म दिवस पर 200 रुपये डालती है और आगे जारी रखती है।जब उसकी पुत्री 21 वर्ष की हो जाएगी तो उसकी गुल्लक में कितनी धनराशि हो जाएगी?
प्रश्नः2.समान्तर श्रेढ़ी किसे कहते हैं? (What is Arithmetic Progression?):
Solution:समान्तर श्रेढ़ी संख्याओं की एक ऐसी सूची है जिसमें प्रत्येक पद (पहले पद के अतिरिक्त) अपने पद में एक निश्चित संख्या जोड़ने पर प्राप्त होता है।
प्रश्न:3.समान्तर श्रेढ़ी के पदों को तथा श्रेणी को कैसे दर्शाते हैं? (How do you Represent Terms and Series of Arithmetic Progression?):
उत्तर:A.P. के पहले पद को a_1, दूसरे पद को a_2,…., nवें पद को a_{n} तथा सार्व अन्तर को d से व्यक्त करें।तब A.P.; a_1, a_2, a_3, \ldots, a_n हो जाती है।व्यंजक a_1+a_2+a_3+\cdots+a_n को श्रेणी कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10),समान्तर श्रेढ़ी कक्षा 10 (Arithmetic Progression Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Arithmetic Progression in Class 10
कक्षा 10 में समान्तर श्रेढ़ी
(Arithmetic Progression in Class 10)
Arithmetic Progression in Class 10
कक्षा 10 में समान्तर श्रेढ़ी (Arithmetic Progression in Class 10) के इस आर्टिकल में कुछ
कठिन सवालों का अध्ययन करेंगे।ये ऐच्छिक प्रश्नावली के सवाल हैं।
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
