Pole and Polar Plane of Conicoids
1.सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Conicoids),त्रिविमीय निर्देशांक ज्यामिति में सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Central Conicoids in 3D):
सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Conicoids) के इस आर्टिकल में ध्रुवीय तल का समीकरण,ध्रुवीय रेखाएँ तथा ज्ञात केन्द्र वाला परिच्छेद के बारे में अध्ययन करेंगे।
ध्रुवीय तल का समीकरण (Equation of the Polar Plane):
बिन्दु A(\alpha, \beta, \gamma) का सकेन्द्र शांकवज A x^2+B y^2+C z^2=1 के सापेक्ष ध्रुवीय तल का समीकरण ज्ञात करना।(To find the equation of the polar plane of the point A(\alpha, \beta, \gamma)[/katex] with respect to the central conicoid A x^2+B y^2+C z^2=1):
माना A(\alpha, \beta, \gamma) से गुजरने वाली किसी रेखा का समीकरण
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}=r (मान लो)
है जहाँ l,m,n रेखा की दिक्कोज्याएँ हैं।
इस रेखा पर स्थित कोई बिन्दु (\alpha+l r, \beta+m r, \gamma+n r) अगर दिए हुए शांकवज का प्रतिच्छेदन बिन्दु हो तो
A(\alpha+l r)^2+B(\beta+m r)^2+C(\gamma+nr)^2=1 \\ \Rightarrow r^2\left(A l^2+B m^2+C n^2\right)+2 r \left(A \alpha l+B \beta m+C \gamma n\right)+\left(A \alpha^2+B \beta^2+C \gamma^2-1\right)=0 \ldots(2)
माना कि r के दो मान r_{1} तथा r_{2} हैं जिससे यदि प्रतिच्छेदन बिन्दु P तथा Q हों तो AP=r_{1} तथा AQ=r_{2}
यदि रेखा APQ पर R(x,y,z) एक ऐसा बिन्दु लें कि AR=r तब ध्रुवीय तल की परिभाषानुसार
r=\frac{2 r_{1} r_{2}}{r_1+r_2}=\frac{\left(A \alpha^2+B \beta^2+C \gamma^2-1\right)}{(A \alpha l+B \beta m+C \gamma n)} \\ \Rightarrow A \alpha(l r)+B \beta(m r)+C \gamma(n r)+ \left(A \alpha^2+B \beta^2+C \gamma^2-1\right)=0 \ldots(3)
अब R(x,y,z) का बिन्दुपथ ज्ञात करने के लिए समीकरणों (1) तथा (3) से l,m,n का विलोपन करने पर:
A \alpha(x-\alpha)+B \beta(y-\beta)+C \gamma(z-\gamma)+ \left(A \alpha^2+B \beta^2+C \gamma^2-1\right)=0 \\ \Rightarrow A \alpha x+B \beta y+C \gamma z=1 \cdots(4)
जो कि बिन्दु A(\alpha, \beta, \gamma) के ध्रुवीय-तल का अभीष्ट समीकरण है।
बिन्दु A(\alpha, \beta, \gamma) ध्रुवीय तल (4) का शांकवज के सापेक्ष ध्रुव है।
विशेष स्थिति (Particular Case):
बिन्दु (\alpha, \beta, \gamma) का दीर्घवृत्त के सापेक्ष ध्रुवी समतल का समीकरण होगाः
\frac{\alpha x}{a^2}+\frac{\beta y}{b^2}+\frac{\gamma z}{c^2}=1
ध्रुवीय रेखा का समीकरण (Equation of Polar Line):
रेखा \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} का सकेन्द्र शांकवज A x^2+B y^2+C z^2=1 के सापेक्ष ध्रुवीय रेखा के समीकरणों को ज्ञात करना (To find equation to the polar line \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} of the given line with respect to the conicoid A x^2+B y^2+C z^2=1.)
दी हुई रेखा \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}=r(मान लो) पर किसी बिन्दु \left ( \alpha+lr,\beta+mr,\gamma+nr \right ) का शांकवज A x^2+B y^2+C z^2=1 के सापेक्ष ध्रुवीय तल का समीकरण होगा
A(\alpha+l r) x+B(\beta+m r) y+C\left(\gamma+n r\right) z=1 \\ \Rightarrow(A \alpha x+B \beta y+C \gamma z-1)+r(A l x+B m y+Cn z)=0 \ldots(1)
यह तल,r के सभी मानों के लिए समतलों
A \alpha x+B \beta y+C \gamma z-1=0
तथा A l x+B m y+C n z=0
की प्रतिच्छेदन रेखा से गुजरता है।अतः दी हुई रेखा \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} की शांकवज A x^2+B y^2+c z^2=1 के सापेक्ष ध्रुवीय रेखा (Polar line) के समीकरण होंगे:
\left.\begin{matrix} A \alpha x+B \beta y+C \gamma z=1 \\ A l x+B m y+C n z=0 \end{matrix} \right\} \ldots(2)
ज्ञात केन्द्र वाला परिच्छेद (Section with a given centre):
एक बिन्दु (\alpha, \beta, \gamma) पर समद्विभाजित होने वाली शांकवज A x^2+B y^2+c z^2=1 की जीवाओं का बिन्दुपथ ज्ञात करना।
[To find the locus of chords of the central conicoid A x^2+B y^2+c z^2=1 which are bisected at the point (\alpha, \beta, \gamma)]
मान लो बिन्दु (\alpha, \beta, \gamma) से गुजरने किसी जीवा का समीकरण है:
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}=r(मान लो) ......(1)
इस पर कोई बिन्दु \left ( \alpha+lr,\beta+mr,\gamma+nr \right ) शांकवज A x^2+B y^2+c z^2=1 पर स्थित होगा यदि
A\left(\alpha+l r\right)^2+B(\beta+m r)^2+C(\gamma+n r)^2=1 \\ \Rightarrow r^2\left(A l^2+B m^2+Cn^{2})+2 r(A \alpha l+B \beta m+C \gamma n\right)+\left(A \alpha^2+B \beta^2+C \gamma^2-1\right)=0 \ldots(2)
यह r में द्विघात समीकरण है अतः r के दोनों मानों के संगत शांकवज पर दो बिन्दु होंगे।चूँकि (\alpha, \beta, \gamma) इन दोनों बिन्दुओं को मिलनेवाली जीवा का मध्य-बिन्दु है इसलिए r_1+r_2=0 अर्थात्
A \alpha l+B \beta m+C \gamma n=0 \ldots(3)
समीकरणों (1) तथा (3) में से l,m,n का विलोपन करने पर अभीष्ट बिन्दुपथ होगाः
A(x-\alpha) \alpha+B(y-\beta) \beta+C(z-\gamma) \gamma=0 \\ \Rightarrow A \alpha x+B \beta y+C \gamma z=A \alpha^2+B \beta^2+C \gamma^2 \ldots(4)
टिप्पणी:यदि S \equiv A x^2+B y^2+C z^2-1 \\ S_1 \equiv A \alpha^2+B \beta^2+C \gamma^2-1 \\ T \equiv A \alpha x+B \beta y+C \gamma z-1
तो समीकरण (4) को निम्न प्रकार लिखा जा सकता है
T=S_1 \ldots(5)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Central Conicoids in 3D
2.सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल के साधित उदाहरण (Pole and Polar Plane of Conicoids Solved Examples):
Example:1.सिद्ध कीजिए कि शांकवज a x^2+b y^2+c z^2=1 के सापेक्ष समतल का ध्रुव बिन्दु \left(\frac{l}{a p},\frac{m}{b p} ,\frac{n}{c p}\right) है।
(Prove that the pole of the plane lx+my+nz=p with respect to the conicoid a x^2+b y^2+c z^2=1 is the point \left(\frac{l}{a p},\frac{m}{b p} ,\frac{n}{c p}\right).)
Solution:मान लो दिए हुए समतल का शांकवज के सापेक्ष ध्रुव (\alpha, \beta, \gamma) है तब इसकी शांकवज के सापेक्ष ध्रुव का समीकरण होगा
a x \alpha+b y \beta+c z \gamma=1 \ldots(1)
यहाँ दिए हुए समतल का समीकरण है
lx+my+nz=p …. (2)
(1) व (2) एक ही समतल के समीकरण हैं अतः इनकी तुलना करने पर:
a \alpha=\frac{l}{p} \Rightarrow \alpha=\frac{l}{a p} \\ b \beta=\frac{m}{p} \Rightarrow \beta=\frac{m}{b p} \\ c \gamma=\frac{n}{p} \Rightarrow \gamma=\frac{n}{c p}
अतः ध्रुव बिन्दु \left(\frac{l}{ap}, \frac{m}{b p}, \frac{n}{c p}\right)
Example:2.सिद्ध कीजिए कि शांकवज x^2-2 y^2+3 z^2-4=0 के सापेक्ष रेखा \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4} की ध्रुवीय रेखा है:
(Prove that the polar line of with respect to the conicoid x^2-2 y^2+3 z^2-4=0 is \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4})
Solution:शांकवज का समीकरण: x^2-2 y^2+3 z^2-4=0 \cdots(1)
दी हुई रेखा:
\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4} \cdots(2)
केन्द्रीय शांकवज के सापेक्ष ध्रुवीय रेखा का समीकरण :
\left(\frac{1}{4}\right) x^2-\left(\frac{1}{2}\right) y^2+\left(\frac{3}{4}\right) z^2=1 \\ \left(\frac{1}{4}\right)(1) x+\left(-\frac{1}{2}\right)(2) y+\left(\frac{3}{4}\right)(3) z=1
तथा \left(\frac{1}{4}\right)(2) x+\left(-\frac{1}{2}\right)(3) y+\left(\frac{3}{4}\right)(4) z=0 \\ \Rightarrow x-4 y+9 z=4
तथा x-3 y+6 z=0
(x+6)-4(y-2)+9(z-2)=0
(x+6)-3(y-2)+6(z-2)=0
युगपत समीकरणों को हल करने पर:
\frac{x+6}{-24+27}=\frac{y-2}{9-6}=\frac{z-2}{-3+4} \\ \Rightarrow \frac{x+6}{3}=\frac{y-2}{3}=\frac{z-2}{1}
Example:3.गोले x^2+y^2+z^2=1 के सापेक्ष रेखा \frac{x+1}{2}=\frac{y-2}{3}=\frac{z+3}{1} की ध्रुवीय रेखा का समीकरण ज्ञात कीजिए।
(Find the equation of the polar line \frac{x+1}{2}=\frac{y-2}{3}=\frac{z+3}{1} of with respect to the sphere x^2+y^2+z^2=1.)
Solution:दी हुई रेखा का समीकरण
\frac{x+1}{2}=\frac{y-2}{3}=\frac{z+3}{1} \ldots(1)
गोले का समीकरण:
x^2+y^2+z^2=1 \cdots(2)
रेखा (1) गोले (2) के सापेक्ष ध्रुवीय रेखा का समीकरण होगा:
(1)(-1)x+(1)(2)y+(1)(-3)z=1
-x+2y-3z=1
\Rightarrow x-2y+3z=-1
(1)(2)x+(1)(3)y+(1)(1)z=0
\Rightarrow 2x+3y+z=0
x-2y+3z=-1,2x+3y+z=0
Example:4.शांकवज 2 x^2-25 y^2+2 z^2=1 के सापेक्ष रेखा - 2x=25y-1=2z की ध्रुवीय रेखा का समीकरण ज्ञात कीजिए।सिद्ध कि यह शांकवज को दो वास्तविक बिन्दुओं P और Q पर मिलती है तथा पुष्टि कीजिए कि P और Q पर खींचे गए स्पर्श समतल दी हुई रेखा से गुजरते हैं।
(Find the equation to the polar of the line 2 x^2-25 y^2+2 z^2=1.Prove that it meets the conicoid in two real points P and Q and verify that the tangent planes at P and Q pass through the given line.)
Solution:दी हुई रेखा का समीकरण:
-2x=25y-1=2z \\ \Rightarrow \frac{x}{-\frac{1}{2}}=\frac{y-\frac{1}{25}}{\frac{1}{25}}=\frac{z}{\frac{1}{2}}=r(माना).....(1)
शांकवज का समीकरण:
2 x^2-25 y^2+2 z^2=1 \cdots(2)
रेखा (1) शांकवज (2) के सापेक्ष ध्रुवीय रेखा का समीकरण:
2(0) x+(-25)\left(\frac{1}{25}\right) y+2(0) z=1 \\ \Rightarrow y+1=0 \\ 2\left (-\frac{1}{2}\right ) x+(-25)\left(\frac{1}{25}\right) y+2\left(\frac{1}{2}\right) z=0 \\ \Rightarrow x+y-z=0, y+1=0
(1) पर स्थित कोई बिन्दु \left(-\frac{1}{2}r, \frac{1}{25}r+\frac{1}{25}, \frac{1}{2}r\right)
यह शांकवज पर होगा:
=2\left(-\frac{1}{2} r\right)^2-25\left(\frac{1}{25} r+\frac{1}{25}\right)^2+2\left(\frac{1}{2} r\right)^2=1 \\ \Rightarrow \frac{r^2}{2}-25\left(\frac{1}{625} r^2+\frac{2}{625} r+\frac{1}{625}\right) +\frac{r^2}{2}=1 \\ \Rightarrow \frac{r^2}{2}-\frac{r^2}{25}-\frac{2}{25} r-\frac{1}{25}+\frac{r^2}{2}=1 \\ \frac{24 r^2}{25}-\frac{2r}{25} -\frac{1}{25}=0 \\ \Rightarrow 24 r^2-2r-1=0
यह r में द्विघात समीकरण है अतः यह शांकवज को दो प्रतिच्छेदन बिन्दुओं पर मिलती है।
Example:5.यदि A(x_{1}, y_{1}, z_{1}) तथा B(x_{2}, y_{2}, z_{2}) दो दिए गए बिन्दु हों तो शांकवज a x^2+b y^2+c z^2=1 के सापेक्ष रेखा AB की ध्रुवीय रेखा का समीकरण ज्ञात कीजिए।
(If and are any two given points then find the equation of polar line of AB with respect to the conicoid a x^2+b y^2+c z^2=1.)
Solution:दी हुई रेखा AB की समीकरण:
\frac{x-x_{1}}{x_{2}-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}=r (माना)
शांकवज का समीकरण:
a x^2+b y^2+c z^2=1 \cdots(2)
(1) पर स्थित कोई बिन्दु
\left [ x_1+r\left(x_2-x_1\right), y+r\left(y_2-y_1\right), z+r(z_{2}-z_{1}) \right ]
शांकवज के सापेक्ष ध्रुवीय समतल का समीकरण:
a x\left[x_1+r\left(x_2-x_1\right)\right]+b y\left[y_1+r\left(y_2-y_1\right)\right] +c z\left[z_1+ r\left(z_2-z_1\right)\right]=1 \\ \Rightarrow \left(a x x_1+b yy_1+c z z_1-1\right)+r\left[a x\left(x_2-x_1\right)+b y\left(y_2-y_1\right)+c z\left(z_2-z_1\right)\right]=0
r के सभी मानों के लिए समतल निम्न रेखा से गुजरता है:
a x x_1+b y y_1+c z z_1-1=0 \ldots(3)\\ a x\left(x_2-x_1\right)+b y\left(y_2-y_1\right)+c z\left(z_2-z_1\right)=0 \ldots(4)
शांकवज की ध्रुवीय रेखा का समीकरण:
a x x_1+b y y_1+c z z_1=1
तथा a x x_2+b y y_2+c z z_2=1
Example:6.दीर्घवृत्तज \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 के सापेक्ष निम्न दो रेखाओं के ध्रुवी रेखाएँ होने की शर्त ज्ञात कीजिए :
(Find the equation that the following lines must be polar lines with respect to the ellipsoid \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1):
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} ; \frac{x-\alpha^{\prime}}{l^{\prime}}= \frac{y-\beta^{\prime}}{m^{\prime}}=\frac{z-\gamma^{\prime}}{n^{\prime}}
Solution:दी हुई रेखा का समीकरण:
दीर्घ का समीकरण:
\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \cdots(2)
रेखा (1) की दीर्घवृत्तज के सापेक्ष ध्रुवीय रेखा का समीकरण:
\frac{\alpha x}{a^2}+\frac{\beta y}{b^2}+\frac{\gamma z}{c^2}-1=0 \cdots(3)
तथा alx+bmy+cnz=0 …. (4)
परन्तु रेखा \frac{x-\alpha^{\prime}}{l^{\prime}}=\frac{y-\beta^{\prime}}{m^{\prime}}=\frac{z-\gamma^{\prime}}{n^{\prime}} रेखा (1) की ध्रुवीय रेखा हो तो यह (3) व (4) में समतल से गुजरती है।अतः ध्रुवी रेखा होने की शर्त
\frac{\alpha \alpha^{\prime}}{a^{2}}+\frac{\beta \beta^{\prime}}{b^2}+\frac{\gamma \gamma^{\prime}}{c^2}-1=0, \frac{l\alpha^{\prime}}{a^2}+\frac{m \beta^{\prime}}{b^2}+\frac{n \gamma^{\prime}}{c^2}=0
तथा \frac{\alpha l^{\prime}}{a^2}+\frac{\beta m^{\prime}}{b^2}+\frac{\gamma n^{\prime}}{c^2}=0, \frac{ l l^{\prime}}{a^2}+\frac{m m^{\prime}}{b^2}+\frac{n n^{\prime}}{c^2}=0
Example:7.वह प्रतिबन्ध ज्ञात कीजिए कि रेखा \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} शांकवज a x^2+b y^2+c z^2=1 के सापेक्ष रेखा \frac{x-\alpha^{\prime}}{l^{\prime}}=\frac{y-\beta^{\prime}}{m^{\prime}}=\frac{z-\gamma^{\prime}}{n^{\prime}} की ध्रुवीय रेखा को प्रतिच्छेदित करे।
(Find the condition that the line \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} should intersect the polar line \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n} of the line with respect to the conicoid a x^2+b y^2+c z^2=1.)
Solution:माना रेखा AB और PQ का समीकरण हैः
\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}
तथा \frac{x-\alpha^{\prime}}{l^{\prime}}=\frac{y-\beta^{\prime}}{m^{\prime}}=\frac{z-\gamma^{\prime}}{n^{\prime}}
शांकवज के सापेक्ष रेखा AB की ध्रुवीय रेखा का समीकरण:
a \alpha x+b \beta y+c \gamma z-1=0 \ldots(1)
तथा alx+bmy+cnz=0 …. (2)
यदि PQ रेखा,AB की ध्रुवीय रेखा (1) व (2) को प्रतिच्छेदित करती है तब PQ पर कोई बिन्दु दोनों समतलों (1) व (2) को r के सभी मानों के लिए सन्तुष्ट करेगा:
\therefore a \alpha\left(\alpha^{\prime}+l^{\prime} r\right)+b \beta\left(\beta^{\prime}+ m^{\prime} r\right)+c\left(\gamma^{\prime}+n^{\prime} r\right)
तथा a l\left(\alpha{\prime}+l^{\prime}r\right)+b m\left(\beta^{\prime}+m^{\prime} r\right)+c n \left(\gamma^{\prime}+n^{\prime} r\right)=0 \\ \Rightarrow \left(a \alpha \alpha^{\prime}+b \beta \beta^{\prime}+c \gamma \gamma^{\prime}-1\right)+r\left(a \alpha l^{\prime}+b \beta m^{\prime}+c \gamma n^{\prime}\right)=0 \cdots(3)
तथा \Rightarrow \left(a l \alpha^{\prime}+b m \beta^{\prime}+c n \gamma^{\prime}+1\right)+r\left(a l l^{\prime}+ b m m^{\prime}+c n n^{\prime}\right)=0 \ldots(4)
(3) व (4) से r का विलोपन करने पर प्रतिबन्ध प्राप्त होता है:
\frac{a \alpha \alpha^{\prime}+b \beta \beta^{\prime}+c \gamma \gamma^{\prime}-1}{a \alpha l^{\prime}+b \beta m^{\prime}+c \gamma n^{\prime}}=\frac{a l \alpha^{\prime}+b m \beta^{\prime}+c n \gamma^{\prime}}{a l l^{\prime}+b m m^{\prime}+c n n^{\prime}} \\ \left(a \alpha l^{\prime}+b \beta m^{\prime}+c\gamma n^{\prime} \right) +\left(a l \alpha^{\prime}+b m \beta^{\prime}+c n \gamma ^{\prime}\right) =\left(a l l^{\prime}+b m m^{\prime}+c n n^{\prime}\right) + \left(a \alpha \alpha^{\prime}+b \beta \beta^{\prime}+c r \gamma^{\prime}-1\right)
Example:8.सिद्ध कीजिए कि (\alpha, \beta, \gamma) से गुजरने वाली रेखाएँ इनकी \frac{x^2}{a+b}+\frac{y^2}{2 a}+\frac{z^2}{2 b}=1 के सापेक्ष ध्रुवीय रेखाओं के लम्बवत है,निम्न शंकु को जनित करेगी:
(Prove that the lines through (\alpha, \beta, \gamma) at right angles to their polars with respect to \frac{x^2}{a+b}+\frac{y^2}{2 a}+\frac{z^2}{2 b}=1 generate the following cone)
(y-\beta) (\alpha z-\gamma x)+(z-\gamma)(\alpha y-\beta x)=0
Solution:दिए हुए शांकवज का समीकरण:
a^{\prime} x^2+b^{\prime} y^2+c^{\prime} z^2=1 \cdots(1)
जहाँ a^{\prime}=\frac{1}{a+b}, b^{\prime}=\frac{1}{2 a}, c^{\prime}=\frac{1}{2 b} \cdots(2)
बिन्दु \left(\alpha, \beta, \gamma\right) से गुजरने वाली रेखा का समीकरण \frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}=r(माना) ....(3)
(1) पर कोई बिन्दु \left ( \alpha+lr,\beta+mr,\gamma+nr \right )
शांकवज के सापेक्ष इस बिन्दु पर ध्रुवीय समतल:
a^{\prime} x(\alpha+l r)+b^{\prime} y(\beta+m r)+c^{\prime} z(\gamma+n r)=1 \\ \left(a^{\prime} \alpha x+b^{\prime} \beta y+c^{\prime} \gamma z-1\right)+r\left(a^{\prime} l x+b^{\prime} m y+c^{\prime} n z\right)=0
r के सभी मानों के लिए यह समतल निम्न रेखा से गुजरता है:
a^{\prime} \alpha x+b^{\prime} \beta y+c^{\prime} \gamma z=1 \\ a^{\prime} l x+b^{\prime} m y+c^{\prime} n z=0
जो कि (3) की शांकवज के सापेक्ष ध्रुवीय रेखा है।इस रेखा की दिक्कोज्या है:
b^{\prime} c^{\prime}(n \beta-m \gamma), c^{\prime}a^{\prime}(l \gamma-n \alpha), a^{\prime} b^{\prime}(m \alpha-l \beta)
यह रेखा (3) के लम्बवत हो तो:
l \cdot b^{\prime} c^{\prime}(n \beta-m \gamma)+m \cdot c^{\prime} a^{\prime} (l \gamma-n \alpha) +n \cdot a^{\prime} b^{\prime}(m \alpha-l \beta)=0 \\ \Rightarrow \frac{\beta}{m a^{\prime}}-\frac{\gamma}{n a^{\prime}}+\frac{\gamma}{n b^{\prime}}-\frac{\alpha}{l b^{\prime}}+\frac{\alpha}{l c^{\prime}}-\frac{\beta}{m c^{\prime}}=0
प्रत्येक पद को lmn से विभाजित करने पर:
\frac{\alpha}{l}\left(\frac{1}{b^{\prime}}-\frac{1}{c^{\prime}}\right)+\frac{\beta}{m}\left(\frac{1}{c^{\prime}}+\frac{1}{a^{\prime}}\right)+\frac{n}{n}\left(\frac{1}{a^{\prime}}-\frac{1}{b^{\prime}}\right)=0 \cdots(4)
(3) व (4) से l,m,n का विलोपन करने पर:
\frac{\alpha}{x-\alpha}\left(\frac{1}{b^{\prime}}-\frac{1}{c^{\prime}}\right)+\frac{\beta}{y-\beta}\left(\frac{1}{c^{\prime}}-\frac{1}{a^{\prime}}\right)+\frac{\gamma}{z-\gamma}\left(\frac{1}{a^{\prime}}-\frac{1}{b^{\prime}}\right)=0\\ \Rightarrow \frac{\alpha}{x-\alpha}(2 a-2 b)+\frac{\beta}{y-\beta}[2 b-(a+b)]+\frac{\gamma}{z-\gamma} \left(a+b-2 a\right)=0\\ \Rightarrow \frac{2 \alpha}{x-\alpha}-\frac{\beta}{y-\beta}-\frac{\gamma}{z-\gamma}=0\\ \Rightarrow 2 x(y-\beta) \cdot(z-\gamma)-\beta(x-\alpha)(z-\gamma)-\gamma(x-\alpha)(y-\beta)=0
उपर्युक्त उदाहरणों के द्वारा सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Conicoids),त्रिविमीय निर्देशांक ज्यामिति में सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Central Conicoids in 3D) को समझ सकते हैं।
3.सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल पर आधारित सवाल (Questions Based on Pole and Polar Plane of Conicoids):
(1.)सिद्ध कीजिए कि \alpha x^2+\beta y^2+\gamma z^2=1 के सापेक्ष a x^2+b y^2+c z^2=1 के स्पर्शतलों के ध्रुवों का बिन्दुपथ निम्न शांकवज है:
(Prove that the locus of the poles of the tangent planes of a x^2+b y^2+c z^2=1 with respect to \alpha x^2+\beta y^2+\gamma z^2=1 is the following conocoid)
\frac{\alpha^2 x^2}{a}+\frac{\beta^2 y^2}{b}+\frac{\gamma^2 z^2}{c}=1
(2.)उन रेखाओं का रेखा पथ ज्ञात कीजिए जो एक स्थिर बिन्दु \left(\alpha, \beta, \gamma\right) से गुजरती है तथा शांकवज a x^2+b y^2+c z^2=1 के सापेक्ष उनकी ध्रुवीयों के लम्बवत है।
(Find the locus of the straight lines drawn through a fixed point and are at right angles to their polars with respect to the conicoid a x^2+b y^2+c z^2=1)
उपर्युक्त सवालों को हल करने पर सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Conicoids),त्रिविमीय निर्देशांक ज्यामिति में सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Central Conicoids in 3D) को ठीक से समझ सकते हैं।
Also Read This Article:-Central Conicoids in 3D Geometry
4.सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Conicoids),त्रिविमीय निर्देशांक ज्यामिति में सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Central Conicoids in 3D) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.शांकवज के ध्रुव और ध्रुवीय समतल को परिभाषित करो।(Define the pole and polar plane of the conicoid):
उत्तर:परिभाषा (Definition):यदि किसी स्थिर बिन्दु A से खींची गई कोई छेदक रेखा शांकवज को (माना) P और Q पर प्रतिच्छेदित करे तो PQ पर बिन्दु R, A का P व Q के सापेक्ष प्रसंवादी संयुग्मी (Harmonic conjugate) अर्थात् AR=\frac{2 A P \cdot A Q}{A P+A Q} का बिन्दुपथ A का शांकवज के सापेक्ष ध्रुवीय तल (Polar plane) कहलाता है तथा A को इस समतल का ध्रुव कहते हैं।
प्रश्न:2.शांकवज के सापेक्ष ध्रुवीय रेखाओं को परिभाषित कीजिए। (Define Polar lines with respect to conicoid):
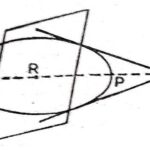
उत्तर:ध्रुवीय रेखाएँ:परिभाषा (Definition):यदि दो सरल रेखाएँ इस प्रकार की हैं कि उनमें से किसी एक रेखा पर स्थित कोई एक बिन्दु का शांकवज के सापेक्ष ध्रुवीय तल दूसरी रेखा से गुजरता है तो ऐसी दशा में ये रेखाएँ शांकवज के सापेक्ष ध्रुवीय रेखाएँ (polar lines) कहलाती हैं।
प्रश्न:3.शांकवज के ध्रुव और ध्रुवीय समतल से सम्बन्धित मुख्य बातें लिखिए।(Write HIGHLIGHTS related to pole and polar plane of conicoid):
उत्तर:(1.) यदि \left(\alpha, \beta, \gamma\right) का ध्रुवीय तल,बिन्दु \left(\alpha^{\prime}, \beta^{\prime}, \gamma^{\prime}\right) से जाता है अर्थात् A \alpha \alpha^{\prime}+B \beta \beta^{\prime}+C \gamma \gamma^{\prime}-1=0 यह स्वविदित है कि \left(\alpha^{\prime}, \beta^{\prime}, \gamma^{\prime}\right) का ध्रुवीय तल \left(\alpha, \beta, \gamma\right) से गुजरेगा।ऐसे दो बिन्दु संयुग्मी (conjugate points) कहलाते हैं तथा ऐसे दो तल संयुग्मी तल (conjugate planes) कहलाते हैं।
(2.)यदि बिन्दु \left(\alpha, \beta, \gamma\right) शांकवज के पृष्ठ पर स्थित है तो \left(\alpha, \beta, \gamma\right) का ध्रुवीय तल उसी बिन्दु पर स्पर्श तल होगा।
(3.)ऐसी दो रेखाएँ जिनमें प्रत्येक शांकवज के सापेक्ष रेखा दूसरी रेखा को काटती है,संयुग्मी रेखाएँ (conjugate lines) कहलाती है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Conicoids),त्रिविमीय निर्देशांक ज्यामिति में सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Central Conicoids in 3D) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Pole and Polar Plane of Central Conicoids
सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल
(Pole and Polar Plane of Central Conicoids)
Pole and Polar Plane of Central Conicoids
सकेन्द्र शांकवज का ध्रुव एवं ध्रुवीय समतल (Pole and Polar Plane of Central Conicoids) के
इस आर्टिकल में ध्रुवीय तल का समीकरण,ध्रुवीय रेखाएँ तथा ज्ञात केन्द्र वाला परिच्छेद के
बारे में अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.









